一 实验目标
绿色方块代表起始位置,红色方块代表目标位置,要求在已知地图全局信息的情况下,规划一条尽可能短的轨迹,控制机器人从绿色走到红色。
给定了迷宫webots模型,地图的全局信息通过读取maze.png这个图片来获取。

二 实验内容与步骤
由于是离线操作,首先对地图进行处理。
步骤一 读取地图信息
2.1.0 配置opencv环境
在图像处理方面,采用了opencv函数库。opencv在图像处理方面有着很强大的功能和很便利的接口,故采用。
而opencv在c++中的配置比较复杂,特别是在windows环境下,搭环境需要花费大量的时间。
第一步是下载opencv函数库,理论上第二步需要源码编译,接着采用makefile链接。据同学反应,源码编译需要长达六个小时,而我搭载了ubuntu的电脑由于太慢了,被我嫌弃了,因此我采用了一个更加巧妙的方法——采用visual studio。visual studio能够很方便地自动生成make文件,这样能够省去很多编写makefile链接的问题。
2.1.1 读取图片
opencv中,图像的存储方式是用一个叫做Mat的结构体。
Mat image = imread("C:\\Users\\birdie\\Desktop\\maze.png");
2.1.2 获取图像的长和宽
结构体Mat中的成员变量rows和cols分别描述图像的行数和列数。
int row = image.rows, col = image.cols;
2.1.3 获取起点和终点
本来是想手动获取图像的起点和终点的坐标信息的,反正都是离线。想想不能这么懒,实现起来也不复杂,而且这样能够使得小车的起点和终点信息更加准确。
采用一个pair描述起点和终点的坐标信息:
pair <int, int> s = find_start(image);
pair <int, int> t = find_end(image);
在我的个人认知当中,绿色在RGB坐标系中,接近于$(0,255,0)$。因此我设定了50的阈值,即R和B小于等于50、G大于200,我便认定其为绿色。采用此区间获得所有的绿色像素的坐标值后,根据绿色的圆环结构,计算出所有绿色像素的平均值,理论上这个平均坐标即为圆心。
然而,事与愿违。在这个阈值内,我没有采集到任何一个绿色像素。当然,功夫不负有心人,我查找到了一个辨别像素的RGB坐标系的网站,网站在附录当中。根据该网站提取的图片中绿色的RGB坐标,如下:

终点的操作与起点同理,终点的红色坐标如下:

由此,通过计算这两个RGB坐标信息的像素坐标的平均坐标,便可得到起点和终点。值得注意的是,在opencv当中,图片的颜色空间是BGR的。
pair<int, int> find_start(Mat& image) {
vector<pair<int, int>> vec;
int row = image.rows, col = image.cols;
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
int pixelB = image.at<Vec3b>(r, c)[0];
int pixelG = image.at<Vec3b>(r, c)[1];
int pixelR = image.at<Vec3b>(r, c)[2];
if (pixelB < 100 && pixelR < 100 && pixelG > 150) {
image.at<Vec3b>(r, c)[0] = 255;
image.at<Vec3b>(r, c)[1] = 255;
image.at<Vec3b>(r, c)[2] = 255;
vec.push_back({ r, c });
}
}
}
int sumx = 0, sumy = 0;
for (auto i : vec) {
sumx += i.first;
sumy += i.second;
}
int tot = (vec.size() == 0) ? 1 : vec.size();
return make_pair(sumx / tot, sumy / tot);
}
2.1.4 转换成二值图像
为了图像处理的便捷性,主要是在连线检测是否撞墙的时候,不希望有太多色彩斑斓的像素,为此,需要将BGR图像转换成二值图像。
转换成二值图像前,首先要转换成灰度图像。由于学过《数字图像处理》这门课程,所以脑海中一直漂浮着一条公式 \(Gray = R*0.299 + G*0.587 + B*0.114\)
随后转念一想,好像不对。opencv中有内置的将BGR图像转换成二值图像的函数,一般而言,内置函数的效率会更高。
cvtColor(image, image, COLOR_BGR2GRAY);
接着就是将灰度图转换成二值图像:
image = change2two(image);
据我所知,这部分其实也有内置函数。但由于在转换的过程中,一是我在函数中写了几个用于debug的打印部分,二是因为这副图像并不是严格的只有黑白红绿四种颜色,在墙体的边缘有着大量的灰色像素,因此这个函数是我手写完成的:
Mat change2two(const Mat& img) {
int row = img.rows, col = img.cols;
Mat image = img.clone();
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
int G = image.at<uchar>(r, c);
if (G < 230)
image.at<uchar>(r, c) = 0;
else
image.at<uchar>(r, c) = 255;
}
}
return image;
}
具体操作很简单,首先clone这副图像,然后遍历整个图像。根据观察, 我认为灰度值小于230的即为黑色部分,原因很简单,因为maze.png中在黑色墙体的边缘中有很多灰色像素,这些尽管更接近白色,但其本质上就是墙体的一部分,因此我认为其也是墙体。
2.1.5 腐蚀
由于小车不是质点,如果小车距离墙体太近,就会撞上墙体。因此不可避免地要对图像进行形态学处理。由于先前已经将图像转换成为了二值图像,因此,我们以小车作为结构元,对道路进行腐蚀(这个操作的逆操作是对墙体膨胀)。
int car_w = 15, car_h = 15;
image = myerode(image, car_w, car_h);
小车的大小在webots的仿真环境中为0.3 x 0.3。根据比例,maze.png在webots仿真环境中的大小为4.5 x 6.0,而maze.png的空间分辨率为600 x 800,因此转换关系为
\(1像素=0.0075米\)
根据转换关系,得到小车的大小为40 x 40。由于小车的坐标中心在小车的重心处,因此只需要保证小车的一边不会与墙体发生碰撞即可。因此,结构元的大小应该为20 x 20。然而事实上,用20 x 20的结构元腐蚀道路后,会发现根本找不到起点到终点的路径,因此采用一个折中的数量级,即15 x 15。实验证明,在大多数情况下,该大小的结构元腐蚀后的道路,既能够找到路径,也不会导致小车与墙体相撞。
腐蚀操作的具体实现为:对于每一个像素值为0的像素,以其为中心,将结构元内的所有像素值置为0。注意的是,这个操作需要两幅图像上完成。
Mat myerode(const Mat& img, int car_w, int car_h) {
int row = img.rows, col = img.cols;
Mat res = img.clone();
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
int G = img.at<uchar>(r, c);
if (G == 0) {
for (int i = max(0, r - car_w); i <= min(row - 1, r + car_w); i++)
for (int j = max(0, c - car_h); j <= min(col - 1, c + car_w); j++)
res.at<uchar>(i, j) = 0;
}
}
}
return res;
}
当然,腐蚀操作在opencv中也有内置函数,不适用的原因在遇到的困难部分有阐述。
2.1.6 统计道路的像素数
统计二值图像中像素值为255的像素的数量。
int cnt = getpixle(image);
具体操作也是遍历整个二值图像:
int getpixle(const Mat& img) {
int row = img.rows, col = img.cols;
int cnt = 0;
for (int r = 0; r < row; r++) {
for (int c = 0; c < col; c++) {
int G = img.at<uchar>(r, c);
if (G != 0 && G != 255)
puts("ERROR!");
if (G == 255)
cnt++;
}
}
return cnt;
}
该操作的目的是为了估计 PRM 算法需要撒点的数量。
步骤二 PRM算法
2.2.1 设置随机种子
srand(time(0));
2.2.2 在地图上随机撒点
随机撒点的原则是
- 点必须在道路上
- 不能有重点
为此,首先设定撒点的数目。由于连线的复杂度是平方级别的,因此撒点的数量不能太多;而如果撒的点的数量太少,则有可能点之间不存在一条从起点到终点的路径。根据上述的计算情况,道路像素有241473个,考虑每200个像素就撒一个点,因此撒1207个点。
int np = cnt / 200;
vector <pair<int, int>> point = getRandPoint(image, np, paint_image);
具体撒点的方法为,迭代1207次,每次找到一个合法的点,若不合法,则重新寻找,直到找到一个合法的点。
vector <pair<int, int>> getRandPoint(const Mat& image, int np, Mat& paint_image) {
map <pair<int, int>, int> exi;
vector <pair<int, int>> point;
int row = image.rows, col = image.cols;
for (int i = 0; i < np; i++) {
int x = rand() % row, y = rand() % col;
while (image.at<uchar>(x, y) == 0 || exi.find({ x, y }) != exi.end()) {
x = rand() % row, y = rand() % col;
}
point.push_back({ x, y });
exi[{x, y}] = 1;
}
return point;
}
实现上,使用一个哈希表exi记录已经出现过的点,每次产生新的点存进一个一维向量point中。
接着将起点和终点也放入向量当中。
point.push_back(s);
point.push_back(t);
2.2.3 连线
首先定义一些初始量:
int npoint = point.size();
int lineDist = 50;
其中,npoint表示撒点数量,lineDist表示距离阈值,即点之间的距离小于等于该阈值,则两点之间连边。
for (int i = 0; i < npoint; i++) {
for (int j = i + 1; j < npoint; j++) {
int dis = (int)sqrt(dist(point[i], point[j]));
if (dis <= lineDist && check(point[i], point[j], image)) {
e[i].push_back({ j, dis });
e[j].push_back({ i, dis });
}
}
}
这部分的实现原理为:对于任意两个点,若两点间的距离小于等于lineDist,且两点的连线直接没有墙体,则将两点连线。具体实现的时候,两点的连线采用邻接链表的形式。
具体展开检查部分,其逻辑结构如下:
int check(pair <int, int> a, pair <int, int> b, const Mat& image) {
if (a.first > b.first) swap(a, b);
int col = image.cols;
if (b.first == a.first) {
... // 当横坐标相等的时候
}
else {
... // 当横坐标不等的时候
}
return 1;
}
当横坐标不相等的时候,我们遍历横坐标,计算出两点连线对应的纵坐标。即已知$(x_a,y_a),(x_b,y_b)$,且满足$x_a<x_b$,那么需要判断的点为: \((x_i,y_i)=(x_i,y_a+\frac{y_b-y_a}{x_b-x_a}\times(x_i-x_a)),x_i\in(x_a,x_b)\) 由于坐标值为整数,因此将该计算出来的浮点数向上取整和向下取整的点都判断一遍。由此会出现一个像素点的偏差,但不影响结果。
double k = 1.0 * (b.second - a.second) / (b.first - a.first);
for (int i = a.first; i < b.first; i++) {
int j = a.second + (int)(1.0 * (i - a.first) * k);
if (j >= 0 && j < col && image.at<uchar>(i, j) == 0)
return 0;
if (j - 1 >= 0 && j - 1 < col && image.at<uchar>(i, j - 1) == 0)
return 0;
if (j + 1 >= 0 && j + 1 < col && image.at<uchar>(i, j + 1) == 0)
return 0;
}
从公式(3)中可以看出,为什么需要划分横坐标是否相等。当横坐标相等的时候,分母为0尽管不会被程序抛出错误,但是在实际连线的图像中,水平连线将会穿过墙体。因此,对于横坐标相等的情况,需要特殊计算,即对横坐标遍历的时候,只有唯一的纵坐标。
if (a.second > b.second) swap(a, b);
for (int i = a.second; i <= b.second; i++) {
if (image.at<uchar>(a.first, i) == 0)
return 0;
}
2.2.4 寻找最短路径
在该部分,我没有采用传统的A※算法,而采用了更加传统的迪杰斯特拉算法。由于点数比较少,采用迪杰斯特拉的复杂度更低。
迪杰斯特拉算法在其他课程中已经熟知,就不再赘述,其算法流程如下:
INITIALIZE-SINGLE-SOURCE $(G, s)$ $S=\varnothing$ $Q=G . V$ while $Q \neq \emptyset$ $u=\operatorname{EXTRACT}-\operatorname{MIN}(Q)$ $S=S \cup\lbrace u\rbrace$ for each vertex $v \in G \cdot A d j[u]$ $\operatorname{RELAX}(u, v, w)$
具体实现为:
void dijstra(const Mat& paint_image, vector <pair<int, int>> &point, int s, int t, int n) {
for (int i = 0; i < n; i++)
d[i] = 1e9;
d[s] = 0;
memset(Last, -1, sizeof(Last));
priority_queue <pair<int, int>> que;
que.push({ 0, s });
while (!que.empty()) {
int u = que.top().second;
que.pop();
for (auto i : e[u]) {
int v = i.first, to = i.second;
if (d[v] > d[u] + to) {
d[v] = d[u] + to;
que.push({ -d[v], v });
Last[v] = u;
}
}
}
vector <pair<int, int>> pat;
for (int i = t; i != s; i = Last[i]) {
int j = Last[i];
line(paint_image, Point(point[i].second, point[i].first), Point(point[j].second, point[j].first), Scalar(170, 0, 136), 2);
pat.push_back({ point[i].first, point[i].second });
}
pat.push_back({ point[s].first, point[s].second });
FILE* fp = fopen("path.txt", "w");
for (int i = pat.size() - 1; i >= 0; i--) {
printf("%d %d\n", pat[i].second, pat[i].first);
fprintf(fp, "%.6lf %.6lf\n", pat[i].second * 0.0075 - 2.25, (799 - pat[i].first) * 0.0075 - 3);
}
}
d[i]表示起点到i的最短路径;用一个堆存储当前已经访问的点集的距离和点的编号,采用堆结构优化使得复杂度降低为O(n log n);Last[i]表示到i号点的最短路径上,上一个点的编号;line函数用于画图;pat用于存储最短路径上点的坐标信息。
最后需要将最短路径经过的结点保存到一个文件当中,以便小车通过坐标信息找路。当然,在图像空间分辨率的坐标和在webots坐标系中的坐标是不一样的,存在一定的转换关系。我们知道,webots坐标系的坐标原点在图像的中心,因此转换关系如下:
\(x=x_p\times 0.0075-2.25,y=(799-y_p\times 0.0075)-3\)
步骤三 小车顶点行驶算法
2.3.1 导入小车
从homework3中导入小车,并将小车的初始位置放置在绿色圈圈的位置附近。注意,小车需要装在GPS。
2.3.2 读取路线点信息
FILE *fp = fopen("path.txt", "r");
double x, y;
queue <pair<double, double>> path;
while (~fscanf(fp, "%lf %lf", &x, &y)) {
path.push({x, y});
}
2.3.3 定点巡线
经过我一番深思熟虑,给定坐标,让小车沿直线到达给定的坐标,我认为有三种实现方式:
- 将路线绘制在地图当中,小车巡线形式;
- 采用纯跟踪算法;
- 采用 PID 算法。
方法一中,小车在巡线的过程中,会出现偏差,一不小心可能会偏离既定的路线。一旦离开路线的范围,很难才能返回既定的路线。因此,不考虑方法一。
纯跟踪算法的实现原理如下:
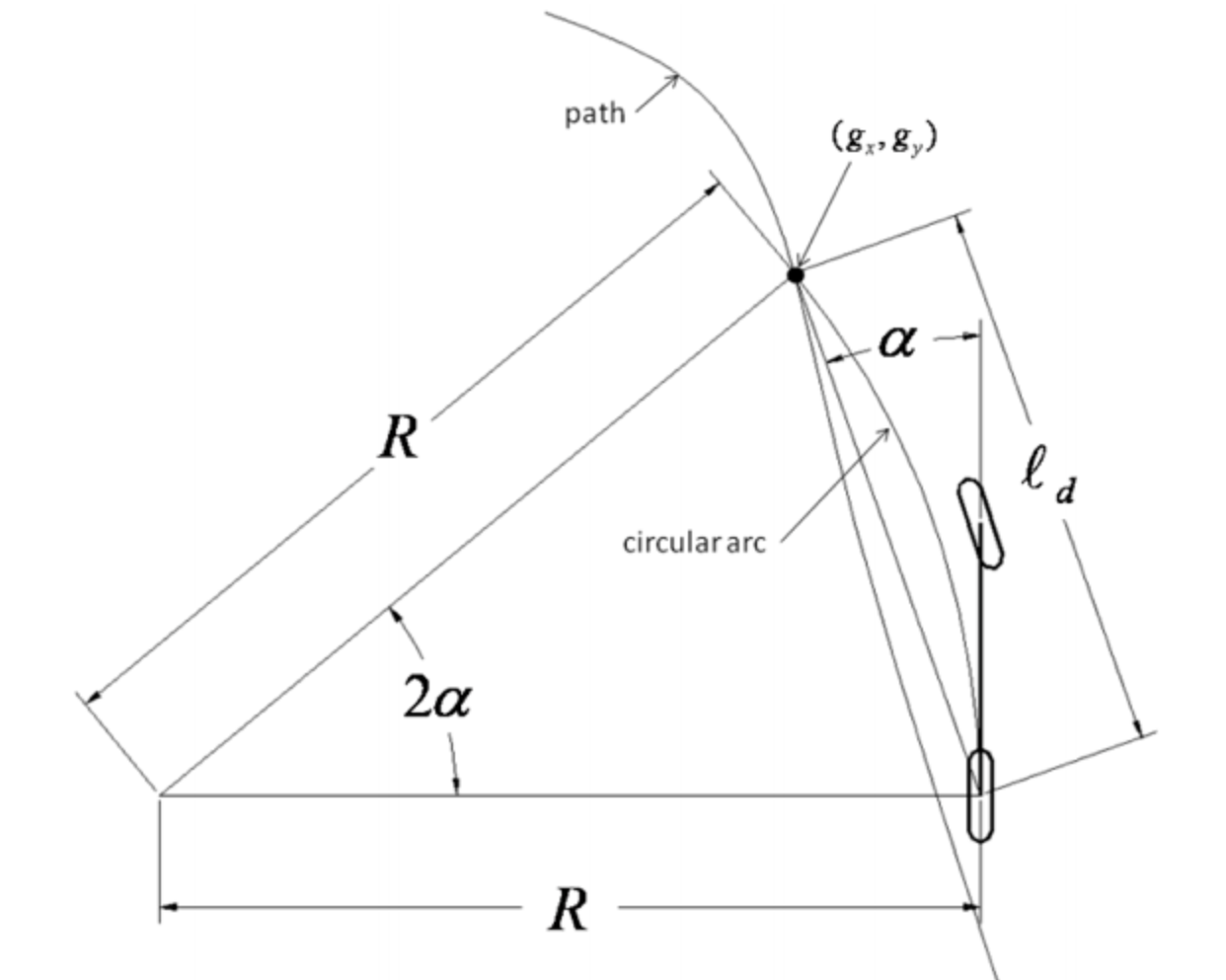
纯跟踪算法从大量的物理推导出发,推导过程比较复杂,由于本次实验的模型不需要这么复杂,我实现的算法中仅仅采取了其中的一点思想,因此不具体推导。
而 PID 算法是一种经典的控制算法,其含义为比例(proportional)、积分(integral)、微分(derivative)。我实现的小车定点移动算法,采用了 PID 和纯跟踪算法的一些思想。
假设小车当前坐标是$(x_0,y_0)$,小车的目标位置是$(x_1,y_1)$,行驶过程中保证小车的速度恒定,假设速度为$v$。将速度沿$x$轴和$y$轴正交分解,$x$轴的速度分量$v_x=\frac{x_0-x_1}{\sqrt{(x_0-x_1)^2+(y_0-y_1)^2}}v$,$y$轴的速度分量$v_y=\frac{y_0-y_1}{\sqrt{(x_0-x_1)^2+(y_0-y_1)^2}}v$。按照这两个速度分量,规定小车的起始角度并保持该角度不变,便可以通过控制速度分量方式控制小车前进。
double error = 0.1;
while (robot->step(timeStep) != -1) {
// 获取当前位置信息
double x = gps->getValues()[0], y = gps->getValues()[1];
// 获取目标点位置信息
double tx = path.front().first, ty = path.front().second;
// 在可允许误差范围内到达目标点
if (fabs(x - tx) <= error && fabs(y - ty) <= error) {
if (path.empty()) break;
continue;
}
double d = sqrt(sqr(x - tx) + sqr(y - ty));
if (x > tx) {
for (int i = 0; i < 4; i++)
speed1[i] = speed_backward[i] * (x - tx) / d;
} else {
for (int i = 0; i < 4; i++)
speed1[i] = speed_forward[i] * (tx - x) / d;
}
if (y > ty) {
for (int i = 0; i < 4; i++)
speed2[i] = speed_rightward[i] * (y - ty) / d;
} else {
for (int i = 0; i < 4; i++)
speed2[i] = speed_leftward[i] * (ty - y) / d;
}
for (int i = 0; i < 4; i++)
wheel[i]->setVelocity(speed1[i] + speed2[i]);
}
可以看到,由于小车具有四个速度分量,分别是前、后、左、右,因此需要分类讨论。
三 实验结果与分析
实验结果
算法寻找的最短路如下:

分析
该最短路线上有33个关键节点,数量在正常范围内。小车行驶过程稳定,经过测试正常。
当然小车的速度可以设置的很快,但是设那么快也没什么必要,仿真的时候倍速播放即可。
四 实验中的问题和解决方法
困难一
opencv中图像的坐标描述方式如下:
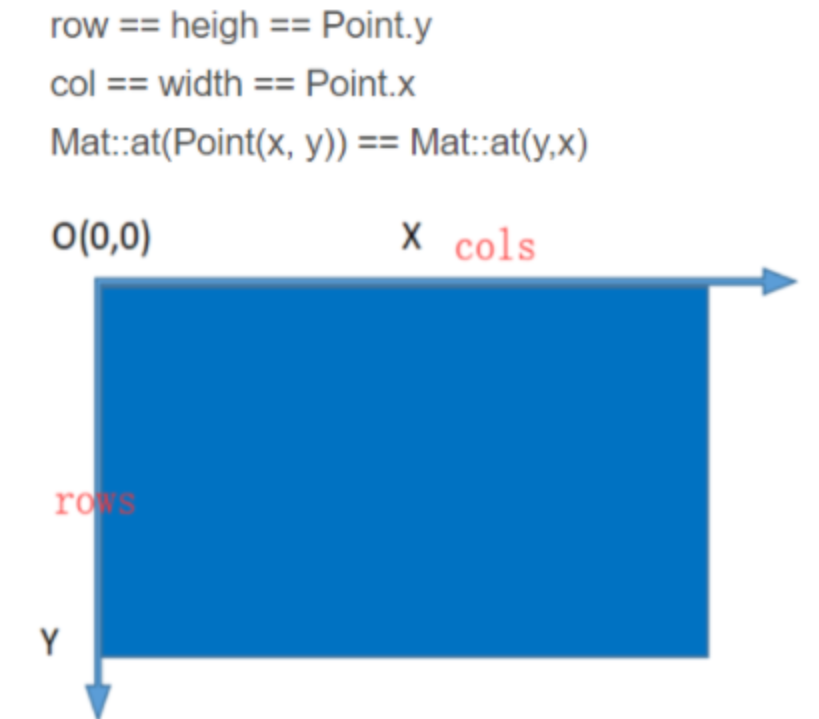
尽管学习过《数字图像处理》这门课程,我还是不能够理解为什么要这么设计图像的坐标读取方式。由于采用at和采用Point描述行和列的方式不一样,而且图像本身存储的方式就和我日常理解的不一样,因此在编写代码的过程中,我常常被搞得晕头转向。
困难二
个人感觉webots内置的c++编译器版本比较老旧,或者说是webots和c++搭配得不是特别完善,在代码中出现了一些诸如%lf写成了%d的时候,会使得3D渲染界面直接崩溃。我一开始以为是控制器或者是小车的问题,后来在控制变量法地调试下,才发现是代码的问题。
困难三
在我浏览的无数篇博文中,opencv的腐蚀操作均为:
int car_w = 15, car_h = 15;
Mat erodeStruct = getStructuringElement(MORPH_RECT, Size(car_w, car_h));
erode(image, image, erodeStruct);
但事实上,在vs中,这种写法过不了编译。我也不知道为什么,处理了很久都没有找到答案。于是我想到了一个很棒的办法——我可以自己写一个腐蚀函数。
还有一个问题就是,理论上腐蚀是需要一个大小为20的结构元的,但是那样找不到一条通路。
后来我改成10,出现了如下结果:

由于腐蚀得太多,使得路径的面积大幅度减少,在撒点数量不多的情况下,很容易找到一条比较长的路径。因此,采取一个折中的方式,将结构元的大小改为15,同时增加撒点的数量。
感想
其实我个人认为,本次实验的难点并不在于 PRM 算法本身。一是我其实并没有使用过opencv,在使用的过程中遇到了不少困难;二是得到关键路线点后,小车移动的算法设计存在一些困难。可能是我太笨了,一度想放弃摆烂。但是功夫不负有心人,总会有柳暗花明的时候,最终还是能够成功完成。