信道噪声特性仿真
产生信道高斯白噪声,设计带通滤波器,把白噪声处理为窄带高斯噪声。对滤波器输入输出的噪声的时域、频域特性进行统计分析,画出相关图形。
高斯白噪声
所谓高斯白噪声中的高斯是指概率分布是正态函数,而白噪声是指它的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。简单定义一下:如果一个噪声,它的瞬时值服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。
首先设置采样频率,采样的总时间,采样的时间点,样本的数量以及噪声功率。
fs = 1000; % 采样频率(Hz)
T_N = 1; % 总时间(s)
t = 1/fs : 1/fs : T_N; % 采样时间点
L = T_N * fs; % 样本数量
power = 3; % 噪声功率(dbw)
matlab中产生高斯白噪声很方便,可以直接使用wgn函数。语法描述:
y = wgn(m,n,p)产生一个m*n的白高斯噪声矩阵。p指定了y的在相对于a瓦特的分贝上能量。缺省的负载阻抗是1欧姆。
值得注意的是,p的单位的dbw,它与W的转换关系为:
\[p(\text{dBw})=10\log P(\text{W})\] 对此,可以直接产生高斯白噪声。
z = wgn(L, 1, power);
为了观察高斯白噪声的频率域图像,首先需要对其进行转换。
-
将噪声从时域转换到频率域。
fft_z = fft(z); % 快速傅里叶变换之后的噪声 -
获得单边频谱。
- fft的结果是关于采样频率的一半对称的,幅度需要除以采样点个数。
- 从双边谱到单边谱需要对非直流分量乘以2。
- 由于奈奎斯特采样定理,原信号的最大频率不会超过采样频率的一半。
fft_z = fft(z); % 快速傅里叶变换之后的噪声 P = abs(fft_z / L); % 取幅频特性,除以L P = P(1 : L/2+1); % 截取前半段 P(2:end-1) = 2 * P(2:end-1); % 单侧频谱非直流分量记得乘以2 f = fs * (0:(L/2)) / L; % 频率,最多到一半(奈奎斯特采样定理)
至此,可以生成高斯白噪声的时域图像和频率域图像:
% 时域图像
subplot(211)
plot(t, z)
title("高斯白噪声时域图像")
xlabel("时间(s)")
ylabel("幅度(v)")
% 频域图像
subplot(212)
plot(f, P)
title("高斯白噪声频域图像")
xlabel("频率(Hz)")
ylabel("幅度(v)")
图像如下:
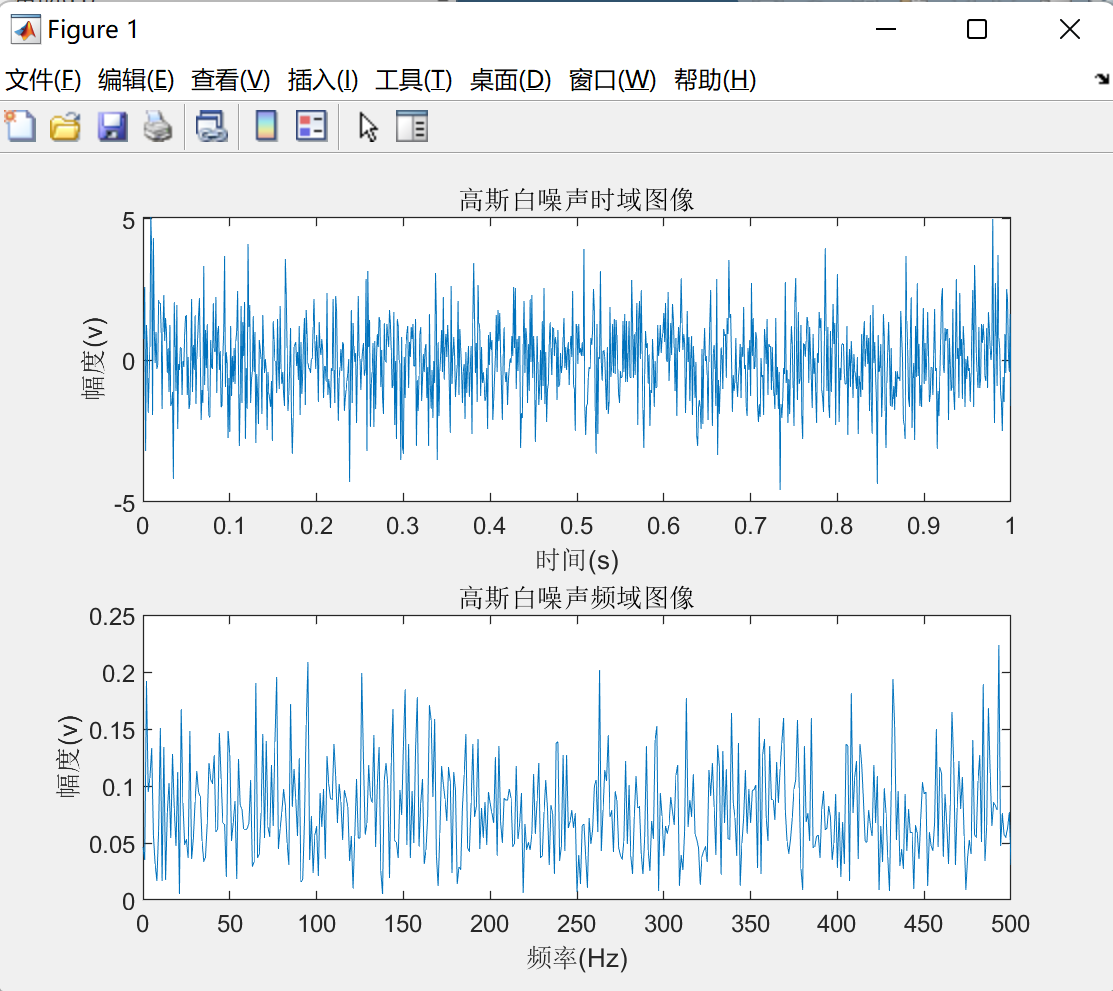
对其进行统计特性分析。分析其自相关函数和功率谱密度。理论上,高斯白噪声的功率谱密度服从均匀分布,幅度分布服从高斯分布。
功率谱密度: \(S_{n}(f)=\frac{N_{0}}{2}\) ,其中 \(\frac{N_{0}}{2}\) 表示双边功率谱密度。 自相关函数: \(R_{n}(\tau)=\frac{N_{0}}{2} \bullet \delta(\tau)\)
matlab提供了函数计算信号的自相关函数:
c = xcorr(x,‘option’)
“unbiased”为无偏的互相关函数估计;
% 自相关函数
subplot(211)
[Cmt, lags] = xcorr(z, 'unbiased');
plot(lags, Cmt);
title('高斯白噪声自相关函数');
同样的,matlab也提供了功率谱密度计算的函数:
[Pxx,f] = periodogram(x,window,nfft,fs)
periodogram是用来计算功率谱密度的,参数中,
X:所求功率谱密度的信号;
window:所使用的窗口,默认是boxcar,其长度必须与x的长度一致;
nfft:采样点数;
fs:采样频率。
% 功率谱密度
subplot(212)
window = boxcar(length(z)); % 矩形窗
[Pmt,f] = periodogram(z,window,L,fs); % 直接法
plot(f, 10 * log10(Pmt));
title('基带信号功率谱密度图');
xlabel('频率');
ylabel('功率');
得到图像如下:
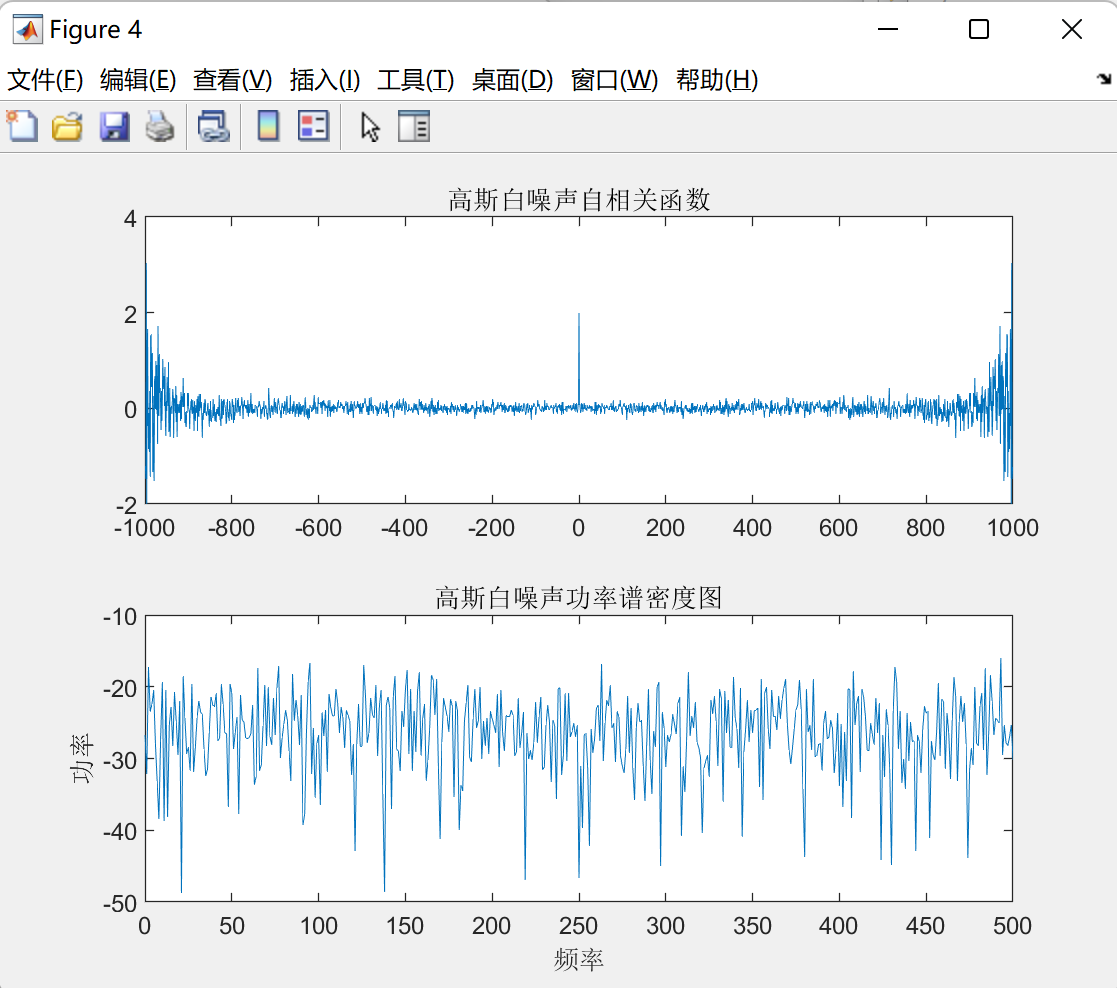
理论上,自相关函数应该是一个单位冲激函数和功率谱密度的乘积。我估计是仿真的时候会出现一些失真的情况,但大体上是符合高斯白噪声的统计特征。
带通滤波器
带通滤波器使用巴特沃斯滤波器。巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。因此,在做仿真时,信号会在第一个周期略微有些失真,但往后的幅频特性就非常的好。这是我们采用的原因之一。
matlab中有直接生成巴特沃斯滤波器的函数,描述如下:
[B,A]=butter(n,[Wn1 Wn2]) %Wn1和Wn2用空格隔开n 是滤波器的阶数,Wn1和Wn2通过的频带,Wn = 截止频率*2/采样频率。
用butter函数获得8阶巴特沃斯滤波器系数,带通范围100-200Hz。
[b,a]=butter(8, [300/(fs/2), 400/(fs/2)]); % 8阶巴特沃斯滤波器系数, 100-200Hz
matlab中有函数可以观察滤波器的特性,描述如下:
freqs(___)没有输出参数时,将在当前图形窗口中绘制幅度和相位响应与角频率的函数关系。
于是观察生成的滤波器的特性:
figure(2)
freqs(b, a) % 画滤波器特性曲线
得到如下图像:
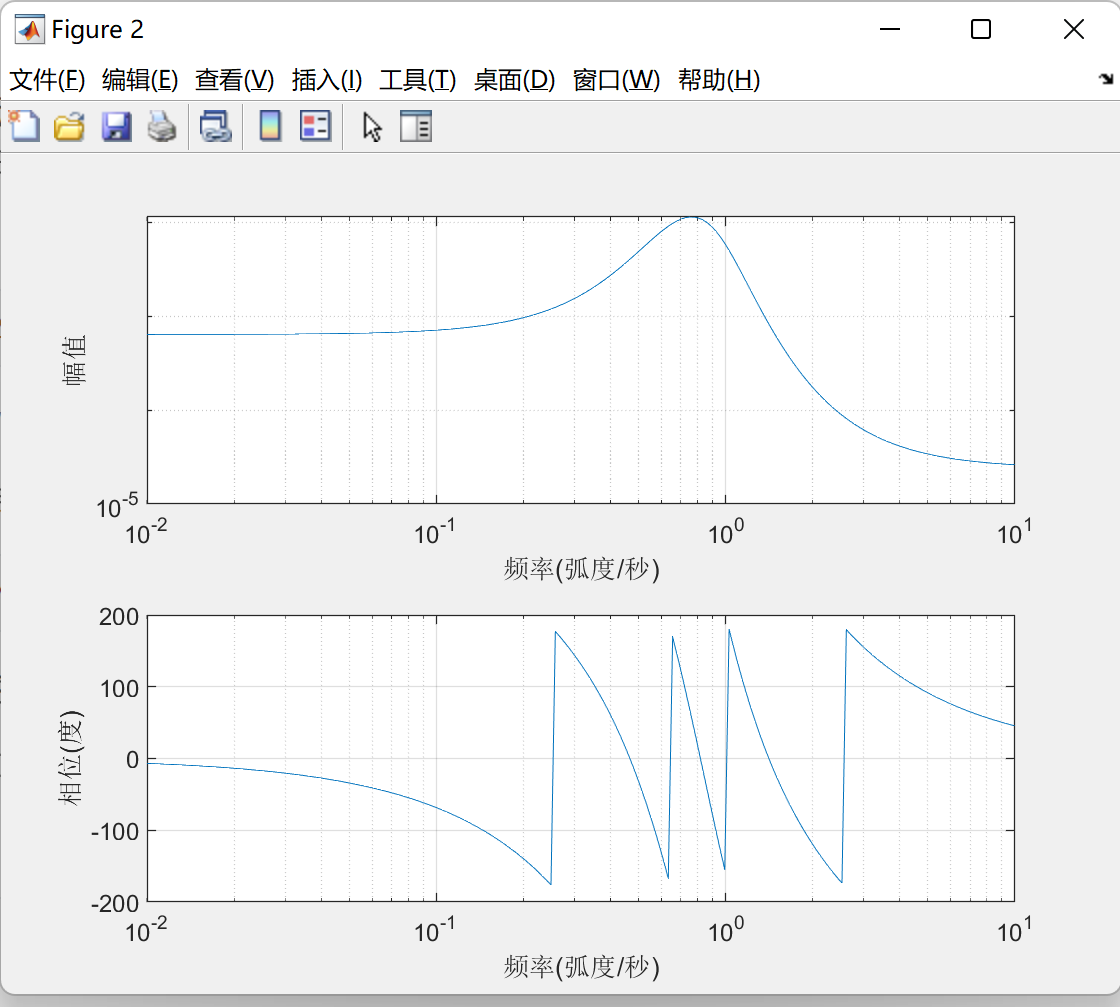
滤波
有了噪声函数和滤波器,就可以对高斯白噪声进行滤波:
lvbo_z=filter(b,a,z); % 滤波
接着做相同的频域转换处理:
fft_lvbo_z = fft(lvbo_z); % 傅里叶变换
P = abs(fft_lvbo_z / L); % 取幅频特性,除以L
P = P(1 : L/2+1); % 截取前半段
P(2:end-1) = 2 * P(2:end-1); % 单侧频谱非直流分量记得乘以2
绘制时域和频域图像:
% 时域图像
figure(3)
subplot(211)
plot((lvbo_z))
title("窄带高斯噪声时域图像")
xlabel("时间(Hz)")
ylabel("幅度(v)")
% 频域图像
subplot(212)
plot(f, P)
title("窄带高斯噪声频域图像")
xlabel("频率(Hz)")
ylabel("幅度(v)")
得到图像:
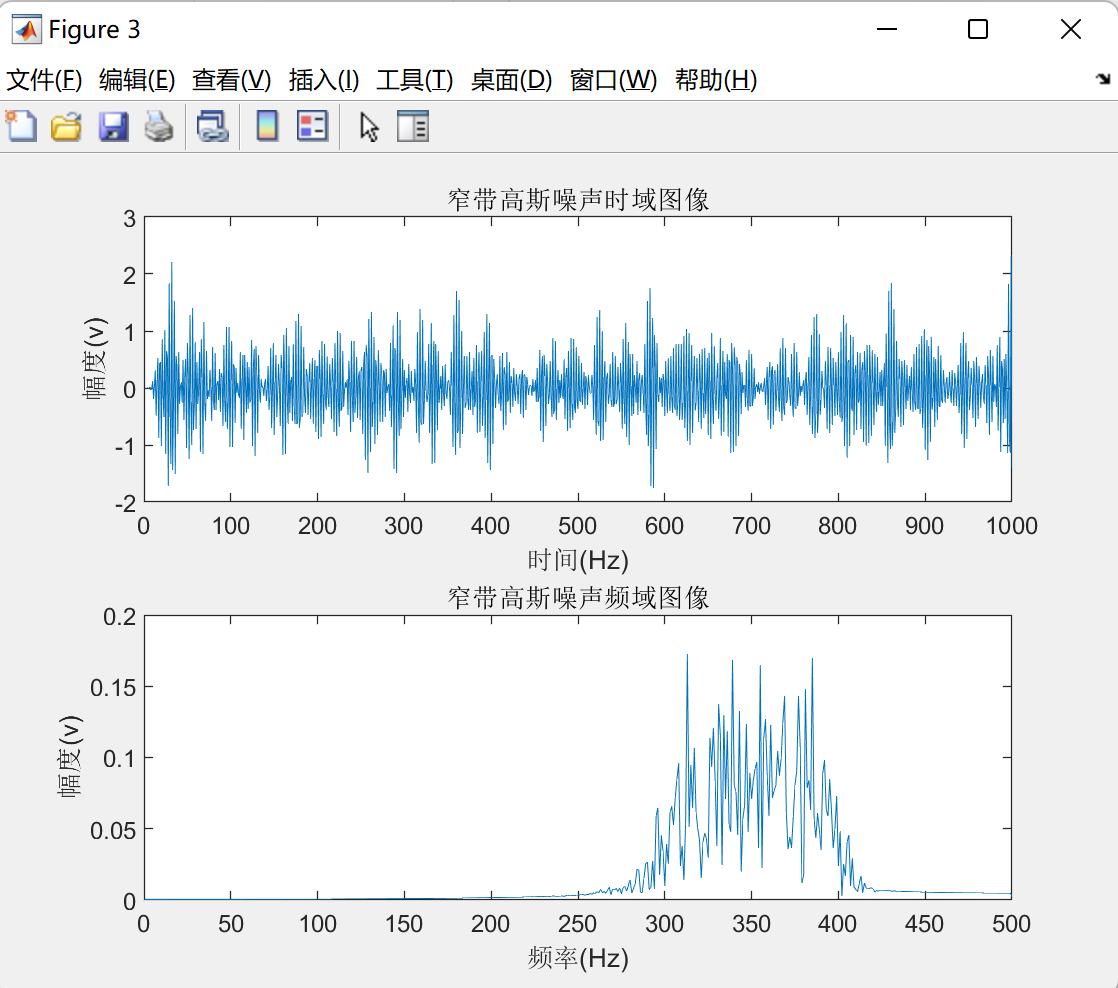
确实是滤波后的效果。
同样地,对其做统计特征分析,分析自相关函数和功率谱密度。
% 自相关函数
subplot(211)
[Cmt, lags] = xcorr(lvbo_z, 'unbiased');
plot(lags, Cmt);
title('高斯白噪声自相关函数');
% 功率谱密度
subplot(212)
window = boxcar(length(lvbo_z)); % 矩形窗
[Pmt,f] = periodogram(lvbo_z,window,L,fs); % 直接法
plot(f, 10 * log10(Pmt));
title('滤波后高斯白噪声功率谱密度图');
xlabel('频率');
ylabel('功率');
得到的结果如图所示:
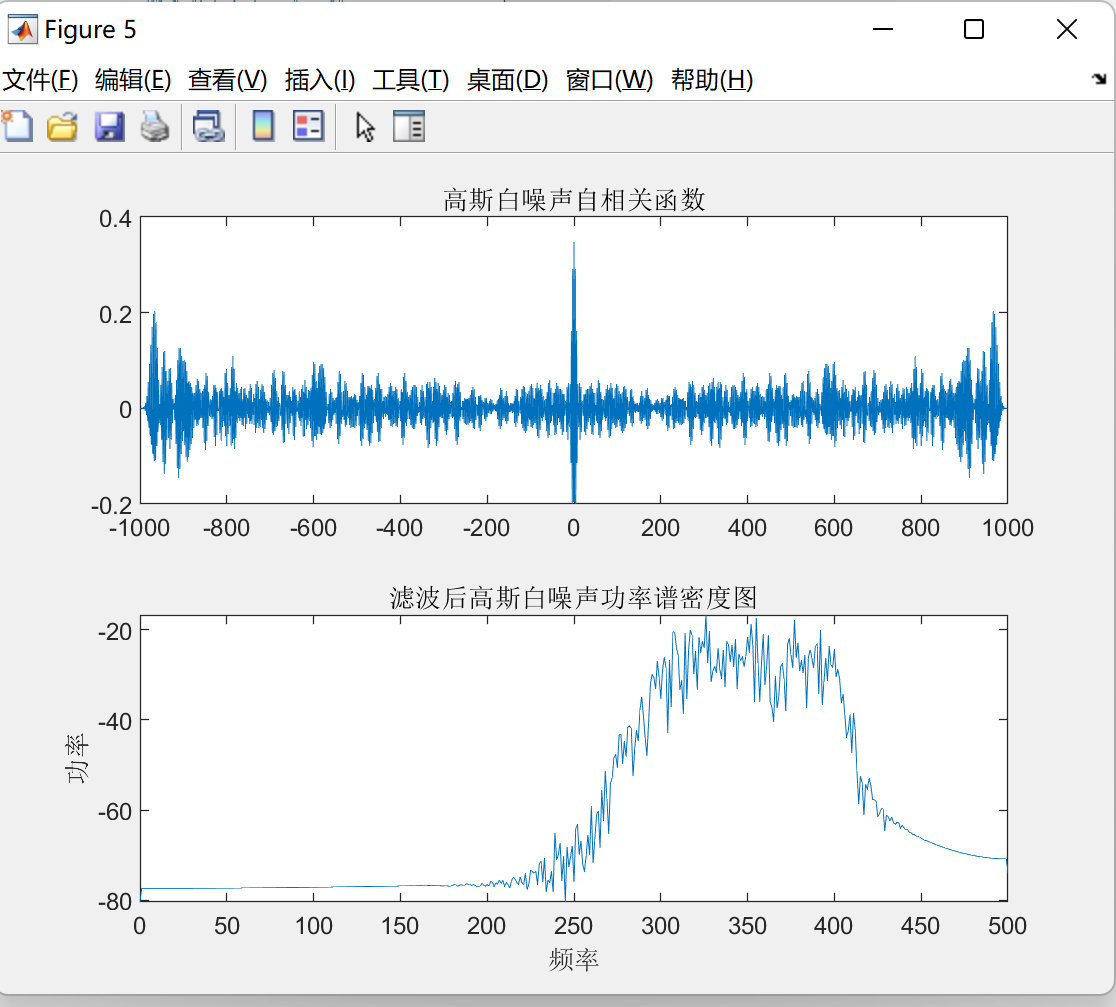
抛去失真的现象,大体上符合统计特征。
附件
完整代码
% 生成高斯白噪声
fs = 1000; % 采样频率(Hz)
T_N = 1; % 总时间(s)
t = 1/fs : 1/fs : T_N; % 采样时间点
L = T_N * fs; % 样本数量
power = 3; % 噪声功率(dbw)
z = wgn(L, 1, power);
% 时域图像
subplot(211)
plot(t, z)
title("高斯白噪声时域图像")
xlabel("时间(s)")
ylabel("幅度(v)")
% 频域图像
fft_z = fft(z); % 快速傅里叶变换之后的噪声
P = abs(fft_z / L); % 取幅频特性,除以L
P = P(1 : L/2+1); % 截取前半段
P(2:end-1) = 2 * P(2:end-1); % 单侧频谱非直流分量记得乘以2
f = fs * (0:(L/2)) / L; % 频率,最多到一半(奈奎斯特采样定理)
subplot(212)
plot(f, P)
title("高斯白噪声频域图像")
xlabel("频率(Hz)")
ylabel("幅度(v)")
figure(4)
% 自相关函数
subplot(211)
[Cmt, lags] = xcorr(z, 'unbiased');
plot(lags, Cmt);
title('高斯白噪声自相关函数');
% 功率谱密度
subplot(212)
window = boxcar(length(z)); % 矩形窗
[Pmt,f] = periodogram(z,window,L,fs); % 直接法
plot(f, 10 * log10(Pmt));
title('高斯白噪声功率谱密度图');
xlabel('频率');
ylabel('功率');
% 生成窄带高斯噪声
[b,a]=butter(8, [300/(fs/2), 400/(fs/2)]); % 8阶巴特沃斯滤波器系数, 100-200Hz
% 滤波器特性图像
figure(2)
freqs(b, a) % 画滤波器特性曲线
lvbo_z=filter(b,a,z); % 滤波
% 时域图像
figure(3)
subplot(211)
plot((lvbo_z))
title("窄带高斯噪声时域图像")
xlabel("时间(Hz)")
ylabel("幅度(v)")
% 频域图像
fft_lvbo_z = fft(lvbo_z); % 傅里叶变换
P = abs(fft_lvbo_z / L); % 取幅频特性,除以L
P = P(1 : L/2+1); % 截取前半段
P(2:end-1) = 2 * P(2:end-1); % 单侧频谱非直流分量记得乘以2
subplot(212)
plot(f, P)
title("窄带高斯噪声频域图像")
xlabel("频率(Hz)")
ylabel("幅度(v)")
figure(5)
% 自相关函数
subplot(211)
[Cmt, lags] = xcorr(lvbo_z, 'unbiased');
plot(lags, Cmt);
title('高斯白噪声自相关函数');
% 功率谱密度
subplot(212)
window = boxcar(length(lvbo_z)); % 矩形窗
[Pmt,f] = periodogram(lvbo_z,window,L,fs); % 直接法
plot(f, 10 * log10(Pmt));
title('滤波后高斯白噪声功率谱密度图');
xlabel('频率');
ylabel('功率');
参考资料
matlab帮助文档