作者的话:说实话,我没搞懂怎么解调,主要书上也没介绍。另外,那个统计分析好像看上去也不怎么对,希望有高人指点。
PM 调制与解调
根据调相的方法。以单频正弦信号为调制信号,仿真实现 PM 调制。并分析调制前后的时域、频域统计特征。基于仿真画出相应的图。
调制函数和载波
首先生成调制函数。设置信号的持续时间,仿真的取样间隔、抽样频率、时间向量。
%% 调制函数
t0 = 0.2; % 信号持续时间
ts = 0.001; % 取样间隔
fs = 1 / ts; % 抽样频率
t = [-t0 / 2 : ts : t0 / 2]; % 时间向量
df = 0.25; % 频率分辨率
m = sin(100 * t); % 调制信号
接着设置载波频率和偏差常数。
fc = 300; % 载波频率
kp = 0.1; % 偏差常数
调制理论
设一个载波可以表示成:
\[c(t)=A\cos\varphi(t)=A\cos(\omega_0t+\varphi_0)\]式中,$\varphi_0$为载波的初始相位;$\varphi(t)=\omega_0+\varphi_0$为载波的瞬时相位;$\omega_0=\text{d}\varphi(t)/\text{d}t$为载波的角频率。
载波的角频率$\omega_0$原本是一个常量。现在将被角度调制后的$\text{d}\varphi(t)/\text{d}t$定义为瞬时频率$\omega_i(t)$,即:
\[\omega_i(t)=\frac{\text{d}\varphi(t)}{\text{d}t}\]它是时间的函数。
由上式可以写出:
\[\varphi(t)=\int\omega_i(t)\text{d}t+\varphi_0\]可见,$\varphi(t)$是载波的相位。若使它随调制信号$m(t)$以某种方式变化,则称其为角度调制。若使相位$\varphi(t)$随$m(t)$线性变化,即令:
\[\varphi(t)=\omega_0t+\varphi_0+k_\text{p}m(t)\]式中,$k_p$是常数,则称其为相位调制。这样,已调信号的表示式为:
\[s_\text{p}(t)=A\cos\ [\omega_0t+\varphi_0+k_\text{p}m(t)]\]调制实验
经过理论分析后,得到调制信号如下:
u = cos(2 * pi * fc * t + 2 * pi * kp * m); % 调制信号
绘制其时域图像。
figure(1)
% 调制信号时域图
subplot(211)
plot(t, m(1 : length(t)))
axis([-0.1, 0.1 -1 1])
xlabel('时间')
title('调制信号时域图像')
% 已调信号时域图
subplot(212)
plot(t, u(1 : length(t)))
axis([-0.1, 0.1 -1 1])
xlabel('时间')
title('已调信号时域图像')
得到图像如下:
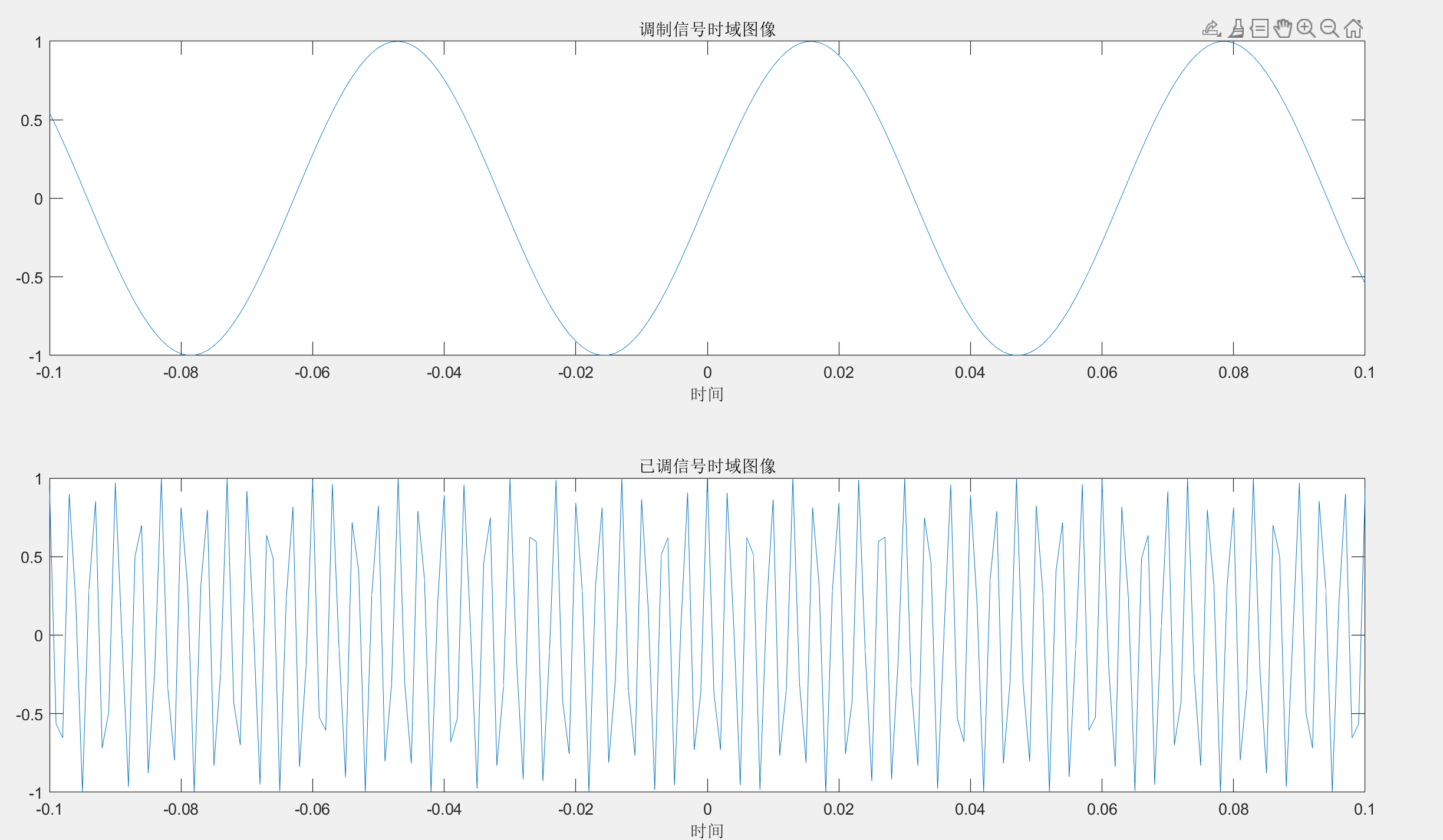
绘制其频谱图:
% 调制信号频谱图
figure(2)
[M, m, df1] = fftseq(m, ts, df); % 傅里叶变换
M = M / fs; % 缩放
f = [0 : df1 : df1 * (length(m) - 1)] - fs / 2; % 频率向量
[U, u, df1] = fftseq(u, ts, df); % 傅里叶变换
U = U / fs; % 缩放
% 调制信号频谱图
subplot(211)
plot(f, abs(fftshift(M)))
axis([-600 600 0 0.04])
xlabel('频率')
title('调制信号频谱图像')
% 已调信号频谱图
subplot(212)
plot(f, abs(fftshift(U)))
axis([-600 600 0 0.04])
xlabel('频率')
title('已调信号频谱图像')
其中,fftseq为fft的一个子函数,其实现为:
% 求傅里叶变换的子函数
function [M, m, df] = fftseq(m, ts, df)
fs = 1 / ts;
if nargin == 2
n1 = 0;
else
n1 = fs / df;
end
n2 = length(m);
n = 2 ^ (max(nextpow2(n1), nextpow2(n2))); % nextpow2(n)取n最接近的较大的2次幂
M = fft(m, n);
m = [m, zeros(1, n - n2)]; % 重构m信号
df = fs / n; % 重新定义频率分辨率
end
目的是为了重新构造fft后的信号和分辨率,使得更加便于图像的观测。
绘制得到的频谱图为:
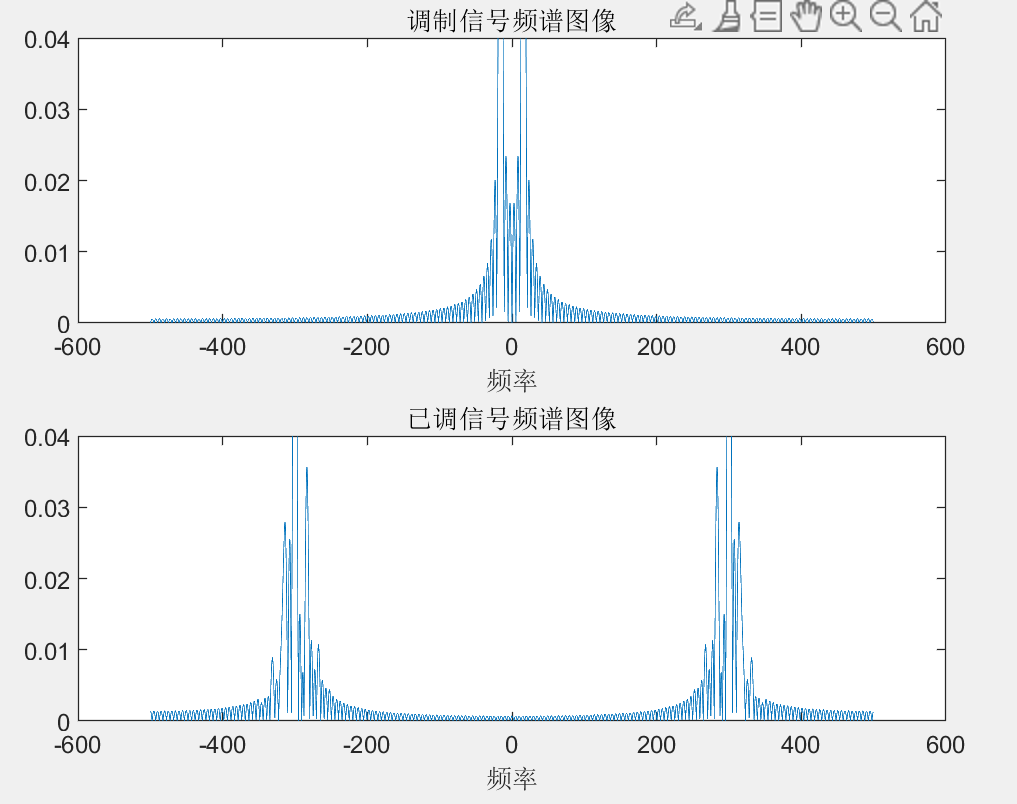
调制后形成相位偏移,整体上频谱图符合预期结果。
对调制信号和已调信号进行统计分析,分析其自相关函数和功率谱密度。
matlab提供了函数计算信号的自相关函数:
c = xcorr(x,‘option’)
“unbiased”为无偏的互相关函数估计;
% 自相关函数
figure(3)
% 调制信号自相关函数
[Cmt, lags] = xcorr(m, 'unbiased');
subplot(211);
plot(lags, Cmt);
title('调制信号自相关函数');
[Cut, lags] = xcorr(u, 'unbiased');
% 已调信号自相关函数
subplot(212);
plot(lags, Cut);
title('已调信号自相关函数');
同样的,matlab也提供了功率谱密度计算的函数:
[Pxx,f] = periodogram(x,window,nfft,fs)
periodogram是用来计算功率谱密度的,参数中,
X:所求功率谱密度的信号;
window:所使用的窗口,默认是boxcar,其长度必须与x的长度一致;
nfft:采样点数;
fs:采样频率。
% 功率谱密度
figure(4)
% 调制信号功率谱密度图
window = boxcar(length(m));
[Pm, f] = periodogram(m, window, length(t), fs);
subplot(211);
plot(f, 10 * log10(Pm));
title('调制信号功率谱密度图');
xlabel('频率');
ylabel('功率');
% 已调信号功率谱密度图
window = boxcar(length(u));
[Pu, f] = periodogram(u, window, length(t), fs);
subplot(212);
plot(f, 10 * log10(Pu));
title('已调信号功率谱密度图');
xlabel('频率');
ylabel('功率');
得到自相关函数和功率谱密度的图像如下所示:
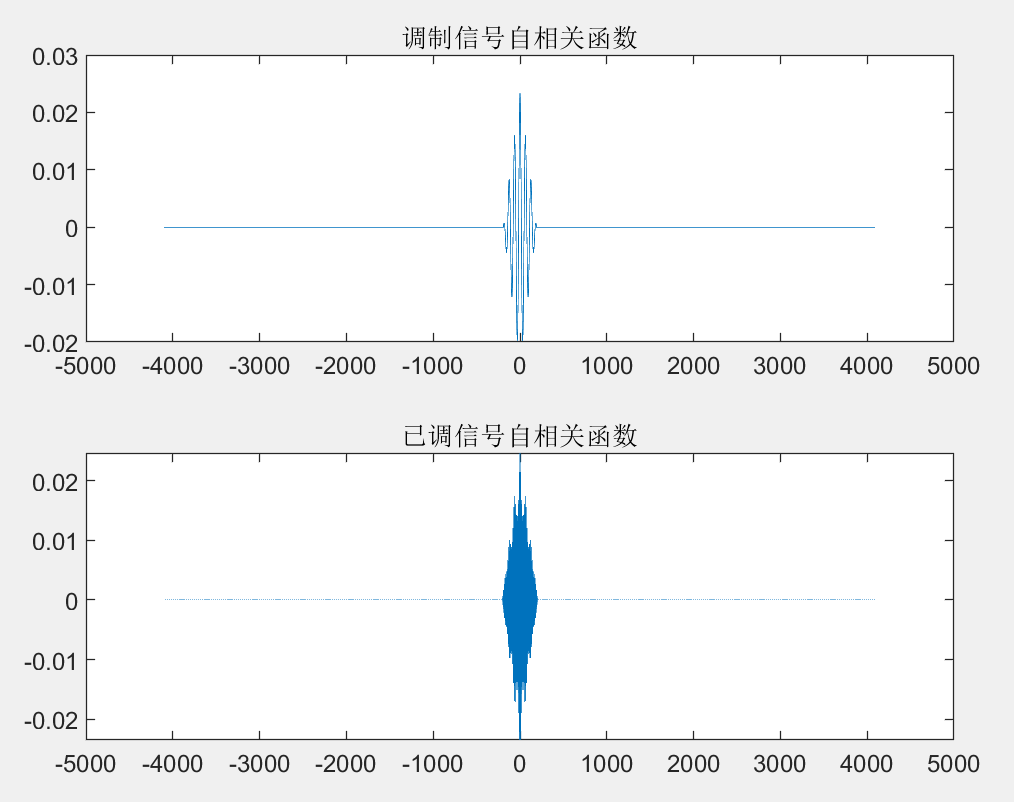
自相关函数符合预期结果。
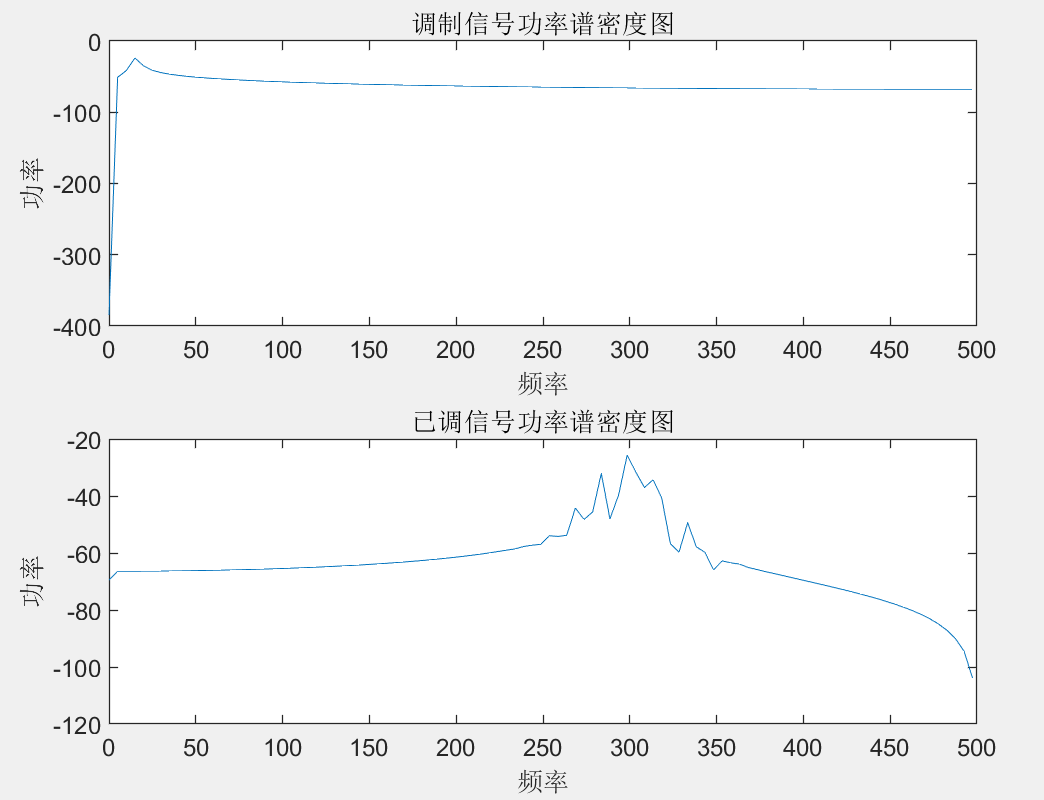
调制后,由于存在失真的情况,图像出现了一些偏差。但整体上符合预期结果。
附件
完整代码如下
%% fftseq.m
% 求傅里叶变换的子函数
function [M, m, df] = fftseq(m, ts, df)
fs = 1 / ts;
if nargin == 2
n1 = 0;
else
n1 = fs / df;
end
n2 = length(m);
n = 2 ^ (max(nextpow2(n1), nextpow2(n2))); % nextpow2(n)取n最接近的较大的2次幂
M = fft(m, n);
m = [m, zeros(1, n - n2)]; % 重构m信号
df = fs / n; % 重新定义频率分辨率
end
主函数:
%% 调制函数
t0 = 0.2; % 信号持续时间
ts = 0.001; % 取样间隔
fs = 1 / ts; % 抽样频率
fc = 300; % 载波频率
t = [-t0 / 2 : ts : t0 / 2]; % 时间向量
kp = 0.1; % 偏差常数
df = 0.25; % 频率分辨率
m = sin(100 * t); % 调制信号
%% 调制
u = cos(2 * pi * fc * t + 2 * pi * kp * m); % 调制信号
%% 画图
figure(1)
% 调制信号时域图
subplot(211)
plot(t, m(1 : length(t)))
axis([-0.1, 0.1 -1 1])
xlabel('时间')
title('调制信号时域图像')
% 已调信号时域图
subplot(212)
plot(t, u(1 : length(t)))
axis([-0.1, 0.1 -1 1])
xlabel('时间')
title('已调信号时域图像')
% 调制信号频谱图
figure(2)
[M, m, df1] = fftseq(m, ts, df); % 傅里叶变换
M = M / fs; % 缩放
f = [0 : df1 : df1 * (length(m) - 1)] - fs / 2; % 频率向量
[U, u, df1] = fftseq(u, ts, df); % 傅里叶变换
U = U / fs; % 缩放
% 调制信号频谱图
subplot(211)
plot(f, abs(fftshift(M)))
axis([-600 600 0 0.04])
xlabel('频率')
title('调制信号频谱图像')
% 已调信号频谱图
subplot(212)
plot(f, abs(fftshift(U)))
axis([-600 600 0 0.04])
xlabel('频率')
title('已调信号频谱图像')
% 自相关函数
figure(3)
% 调制信号自相关函数
[Cmt, lags] = xcorr(m, 'unbiased');
subplot(211);
plot(lags, Cmt);
title('调制信号自相关函数');
[Cut, lags] = xcorr(u, 'unbiased');
% 已调信号自相关函数
subplot(212);
plot(lags, Cut);
title('已调信号自相关函数');
% 功率谱密度
figure(4)
% 调制信号功率谱密度图
window = boxcar(length(m));
[Pm, f] = periodogram(m, window, length(t), fs);
subplot(211);
plot(f, 10 * log10(Pm));
title('调制信号功率谱密度图');
xlabel('频率');
ylabel('功率');
% 已调信号功率谱密度图
window = boxcar(length(u));
[Pu, f] = periodogram(u, window, length(t), fs);
subplot(212);
plot(f, 10 * log10(Pu));
title('已调信号功率谱密度图');
xlabel('频率');
ylabel('功率');
参考资料
《通信原理教程(第四版)》樊昌信.
matlab官方文档.