一 实验目标
绿色方块代表起始位置,红色方块代表目标位置,要求在已知地图全局信息的情况下,规划一条尽可能短的轨迹(采用快速扩展随机树算法),控制机器人从绿色走到红色。
给定了迷宫webots模型,地图的全局信息通过读取maze.png这个图片来获取。

二 实验内容与步骤
由于实际操作与实验四类似,因此,在实验四的基础上作出修改。在此,仅介绍 RRT 的具体实现,其他操作与实验四相同(由于小车的运动规划采用了物理的速度分量偏移模型,在路径点数较多的情况下,仍能够保证小车平稳行驶)。
在具体实现上,将 RRT 算法封装成为一个函数。
getRandomTree(image, paint_image, s, t);
其中 image 是经过灰度图转换、二值化、腐蚀后得到的图像,paint_image 是用于作画的原图像,s 是路径的起点,t 是路径的终点。
步骤一 初始化
首先对一些变量进行初始化,为了保证封装的完整性和可移植性,采用 vector 的形式代替数组。:
const int npoint = 1000; // 随机树的点数
const double epslion = 5; // 生长方向的概率控制
const double dtree = 18.0; // 扩展树扩展的步长
const double dMintree = 16.0; // 避免生长到已生长的距离阈值
srand(time(0)); //设置随机种子
int row = img.rows, col = img.cols; // 图像的行数和列数
vector <pr> res; // 用于存放最终最短路径的结点信息
vector <pr> point; point.push_back(s); // 用于存放随机树的结点信息
vector <double> d; d.push_back(0); // 用于存放随机树结点的距离信息
vector <int> fa; fa.push_back(0); // 用于存放随机树结点的父亲结点
int i; // 循环索引
步骤二 生成随机树
2.2.1 随机采样
首先要确定随机树扩展的方向。大部分情况下,我们希望随机树朝终点的方向生长;而存在一些情况,树朝终点方向生长会出现撞墙的情况,因此,考虑在地图上朝着随机的一个方向生长。因此,需要一个概率阈值的控制,基于地图是迷宫的考量,盲目向终点靠拢会经常出现撞墙,因此设置朝终点方向形式的概率为 50%。
在具体实现上,在每次选择生长方向时,有一定的概率会向着目标点延伸,也有一定的概率会随机在地图内选择一个方向延伸一段距离。
// pr 是 pair <int, int> 的宏定义
/* 返回值是地图上的一个点
* row 是地图的行数
* col 是地图的列数
* t 是终点
*/
pr getToward(int row, int col, pr t) {
int et = rand() % 10;
pr to;
if (et < epslion)
to = t;
else
to = make_pair(rand() % row, rand() % col);
return to;
}
2.2.2 生长点选择
生长点选择与目标点距离最近的一个点,采用遍历所有点的方式实现。当然我有一种设想,对每一行的所有点建立一个队列,这样查询和插入的时间都变成了 log 级别的。但是想想,点数本来就不多,遍历所有点的复杂度也不高,因此没有实现。
// out : id,同时需要得到生长点的索引信息
pr minDist(const vector <pr>& point, pr to, int &id) {
pr closeP; double Min = 1e18; // closeP 为与目标点距离最近的一个点,Min 为最短距离
int rid = 0;
for (auto p : point) {
double d = dist(p, to);
if (d < Min) {
Min = d;
closeP = p;
id = rid;
}
rid++;
}
return closeP;
}
2.2.3 计算随机树新节点
通过生长点和方向,通过计算生长方向的方向向量,得到新的树节点。具体步骤为:
- 计算方向向量
- 计算向量模长,得到单位向量
- 向量正交分解,得到 x 轴方向向量和 y 轴方向向量
- 当前坐标 + 单位正交方向向量 * 生长距离 = 新节点坐标
pr getNewP(pr a, pr b) {
int x = b.first - a.first, y = b.second - a.second;
double d = dist(a, b);
int nx = a.first + (int)(1.0 * x * dtree / d), ny = a.second + (int)(1.0 * y * dtree / d);
pr newP = make_pair(nx, ny);
return newP;
}
2.2.4 判断新节点合法性
判断新结点是否合法有三个衡量指标,假设新节点为$(x,y)$:
- 新坐标在地图中
- 新的树边不会与墙体发生碰撞
- 新的点不在已经生长的区域内
第一个条件,只需要判断$x \times y$是否在$[0, row)\times [0,col)$中即可。
// out = 0 表示不合法,out = 1 表示合法,下同理
bool checkOK(pr p, int row, int col) {
if (p.first < 0 || p.first >= row)
return 0;
if (p.second < 0 || p.second >= col)
return 0;
return 1;
}
第二个条件也很简单,在实验四中已经实现,直接调用即可。
第三个条件,具体实现为:新点与现有的所有点的距离大于某个判断阈值。
bool checkExist(pr newP, const vector <pr> point) {
int cnt = 0;
for (auto i : point) {
double d = dist(newP, i);
if (d < dMintree)
cnt++;
}
if (cnt <= 1)
return 1;
return 0;
}
新点与现有的所有点的距离小于某个判断阈值的点的数量小于等于一即为合法,因为该点与其父亲的距离就小于这个判断阈值。
最终,如果三个条件都通过,则将新节点加入随机树当中,并执行下一轮,否则返回2.2.1。
2.2.5 终止条件
由于我们每次延伸的距离是固定的,所以并不能保证最后一次延伸能够刚好到达终点的位置,更可能的情况是在终点周围来回跳动。因此我们设定一个阈值,假如本次延伸的新点与终点的距离小于这个阈值,我们就认为已经规划成功。
if (dist(newP, t) < dMintree) {
succeed!
end the loop;
}
步骤三 打印路径
由于树上结点只有一个父亲,当第一次访问到终点的时候,迭代结束。因此,从终点开始,不断访问当前结点的父亲,即可得到规划的路径。将该路径写入path.txt当中,放入实验四中的小车模型当中,即可完成实验。
步骤四 修改控制器算法
2.4.1 修改控制器代码
算法同上次实验,区别在于去除了 if 的部分。
double d = sqrt(sqr(x - tx) + sqr(y - ty));
for (int i = 0; i < 4; i++)
speed1[i] = speed_backward[i] * (x - tx) / d;
for (int i = 0; i < 4; i++)
speed2[i] = speed_rightward[i] * (y - ty) / d;
for (int i = 0; i < 4; i++)
wheel[i]->setVelocity(speed1[i] + speed2[i]);
在本次实验中,经过测试,在仿真环境中,PID 控制的小车会产生很严重的抖动,不如开环控制的平稳。具体的闭环控制见期末大作业的代码。
三 实验结果与分析
实验分析
在 RRT 中,对参数的调整格外重要,包括但不限于步长和迭代次数。
当步长设置为 5,迭代次数 1000 次的时候,即随机树的树边的长度为 5 个像素值。
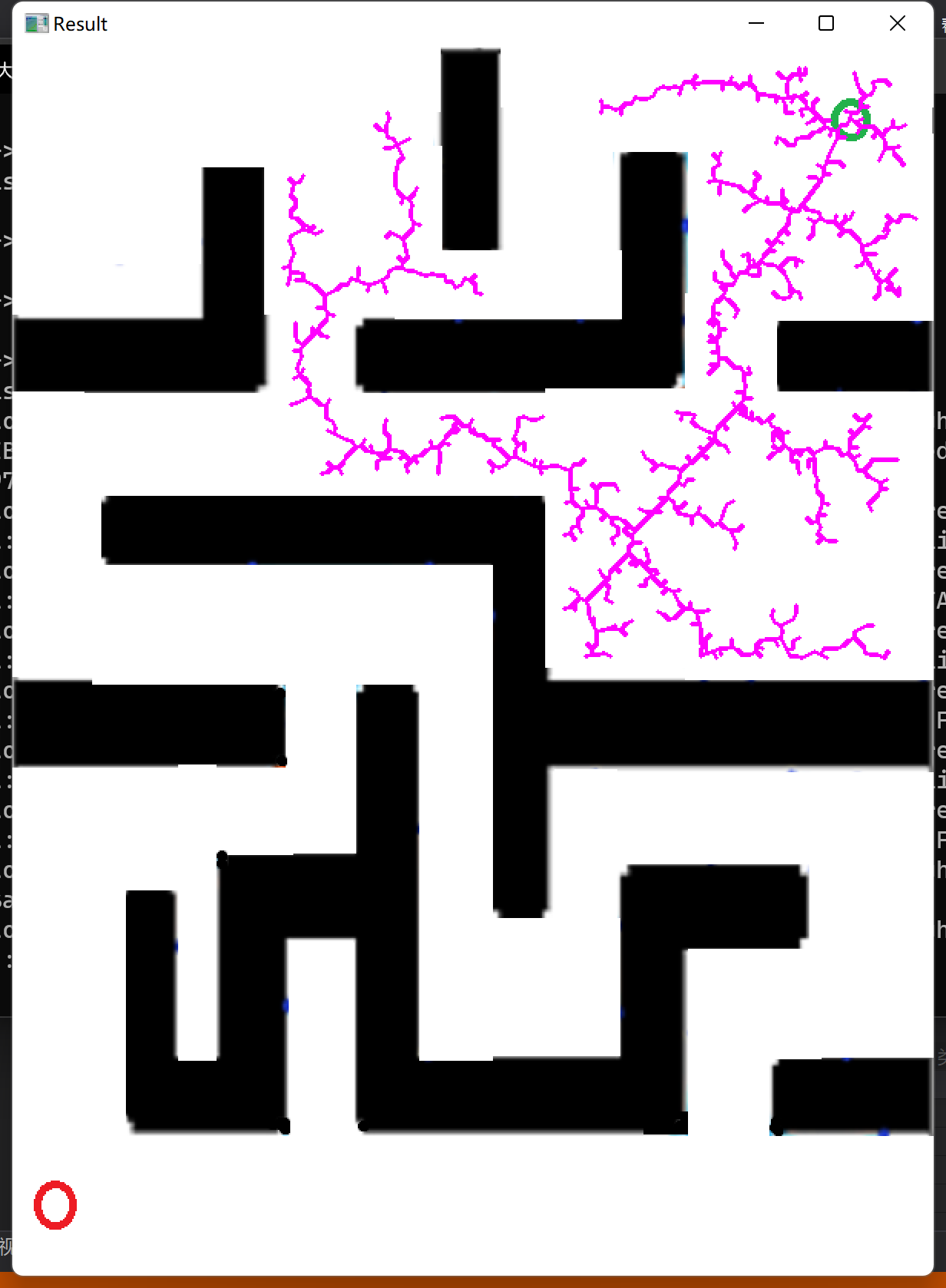
可以发现随机树生长的部分还不到图像的一半。
保持迭代轮数,扩大步长到 8:

图像勉强搜索到一半。
扩大步长到 10,扩到迭代轮数到 1300:

随机树已经初步找到规划路线了。
再次扩大迭代轮数到 1600,保持步长为 10。

规划的路线已经误入歧途了,说明了 RRT 算法有很强的随机性。
保持步长,扩大迭代轮数到 2600。

可以发现点更加密集了,但是仍搜索不到终点,而且计算的时间比较长。我个人认为,点比较密集的原因在于由于步长比较小,导致距离阈值也比较小,因此很容易导致新结点认为撒点的地方仍未被探索,导致比较密集;而点到达不了终点,是因为每次有 50% 的概率在地图上随机撒点,当随机树扩展到一定程度的时候,未探索区域的面积减小,被随机到的概率也会减小,因此如果没有找到一条正确的路径,很有可能会在歧途上徘徊很久;而计算时间比较长,是因为每次判断新结点是否合法的时候,需要遍历所有树节点,而树节点的数量一直在增加,使得计算时间成平方级增长。
因此我改变了策略,增长步长到 18,而减小迭代轮数为 1000。
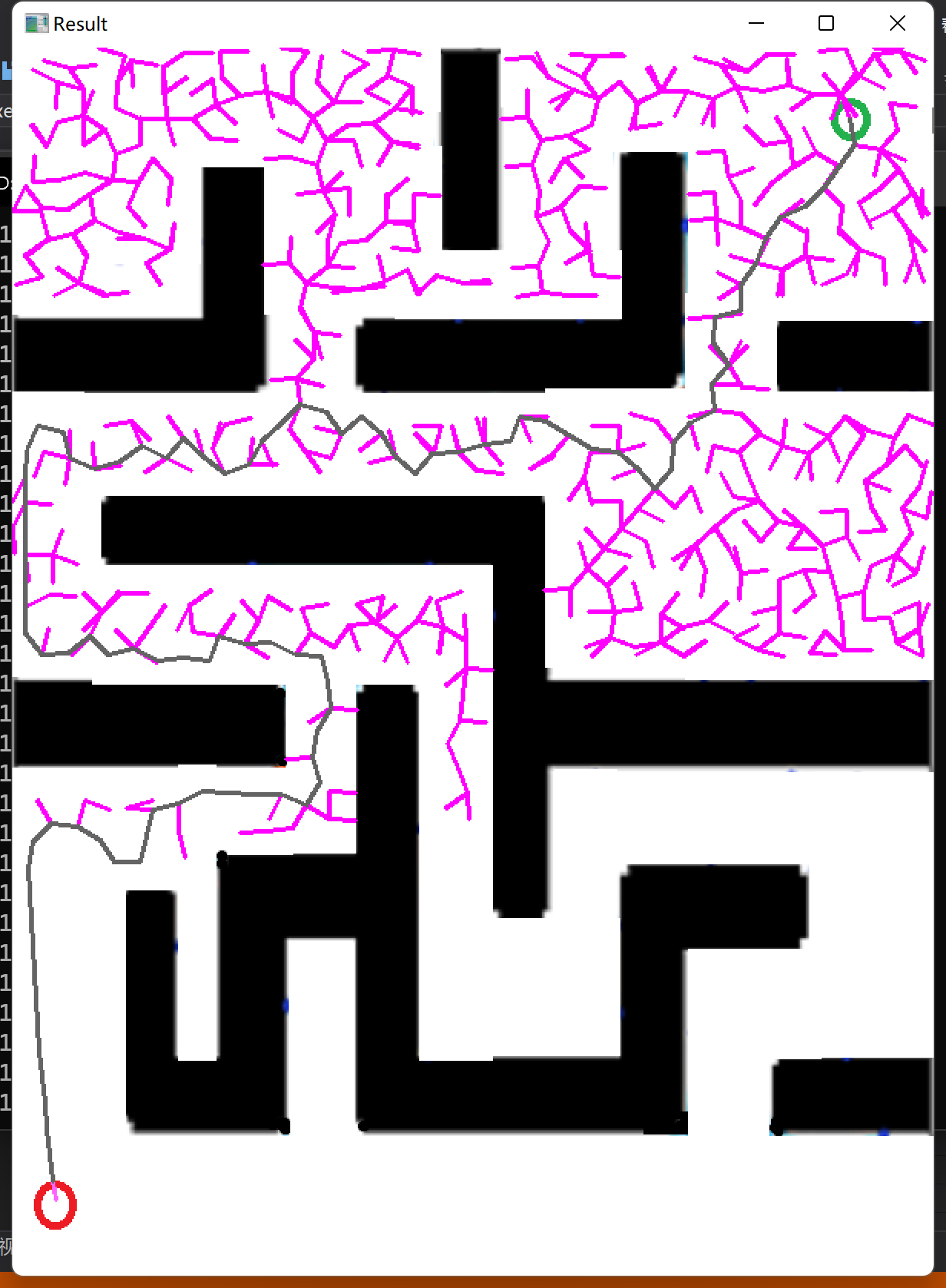
惊喜地发现已经规划出一条比较合理的路线。而实际上,直到访问到终点,只迭代了 426 轮。因此得出结论,步长控制不能设置太短。
其实可以发现,由于在 RRT 中,已经探索过的区域不会再进行探索,因此最终的效果不及 PRM。
实验结果
最终得到的规划路线(深绿色太丑了,我换了一种颜色):

由于小车采用逻辑层控制,不需要小车进行巡线,所以路线不需要平滑。逻辑层控制本来行驶就很平滑。