Abstract
讨论了高斯低通滤波器的原理,并实现了高斯低通滤波器:能够指定生成的二维函数的大小$M\times N$和高斯函数中心的二维位置。
Technical discussion
在这里探讨二维高斯低通滤波器,下面用GLPF表示高斯低通滤波器。
先给出滤波器的二维形式:
\[H(u,v)=e^{-D^2(u,v)/2\sigma^2} \tag1\]其中,$D(u,v)$是距频率矩形中心的距离,$\sigma$是关于中心的拓展度的度量。通过令$\sigma=D_0$,滤波器的表示形式变为:
\[H(u,v)=e^{-D^2(u,v)/2D^2_0}\tag2\]式中,$D_0$是截止频率。当$D(u,v)=D_0$时,GLPF下降到其最大值的0.607处。
GLPF的傅里叶反变换也是高斯的,这意味着通过式(1)或者式(2)的IDFT得到的空间高斯滤波器将没有振铃。
Discussion of results
Lowpass Filtering
(a) Implement the Gaussian lowpass filter in Eq. (4.3-7). You must be able to specify the size, M x N, of the resulting 2D function. In addition, you must be able to specify where the 2D location of the center of the Gaussian function.
具体步骤为:
-
给定一幅大小为$M\times N$的输入图像
f(x,y),得到填充参数P和Q。默认选择P=2M,Q=2N。 -
对
f(x,y)添加必要数量的0,形成大小为$P\times Q$的填充后的图像$f_p(x,y)$。 -
用$(-1)^{2(u_0x/P+v_0y/Q)}$乘以$f_p(x,y)$,移到$(u_0,v_0)$。
-
计算来自步骤3的图像的DFT,得到
F(u,v)。 -
生成一个实的、对称的滤波函数
H(u,v),其大小为$P\times Q$,中心在$(u_0,v_0)$处。用阵列相乘形成乘积$G(u,v) = H(u,v)F(u,v)$;即$G(i,k)=H(i,k)F(i,k)$。 -
得到处理后的图像:
\[g_p(x,y)=\lbracereal[\mathcal{F}^{-1}[G(u,v)]]\rbrace(-1)^{2(u_0x/P+v_0y/Q)}\] -
通过从$g_p(x,y)$的左上象限提取$M\times N$区域,得到最终处理结果
g(x,y)。
(b) Download Fig. 4.11(a) [this image is the same as Fig. 4.18(a)] and lowpass filter it to obtain Fig. 4.18(c).
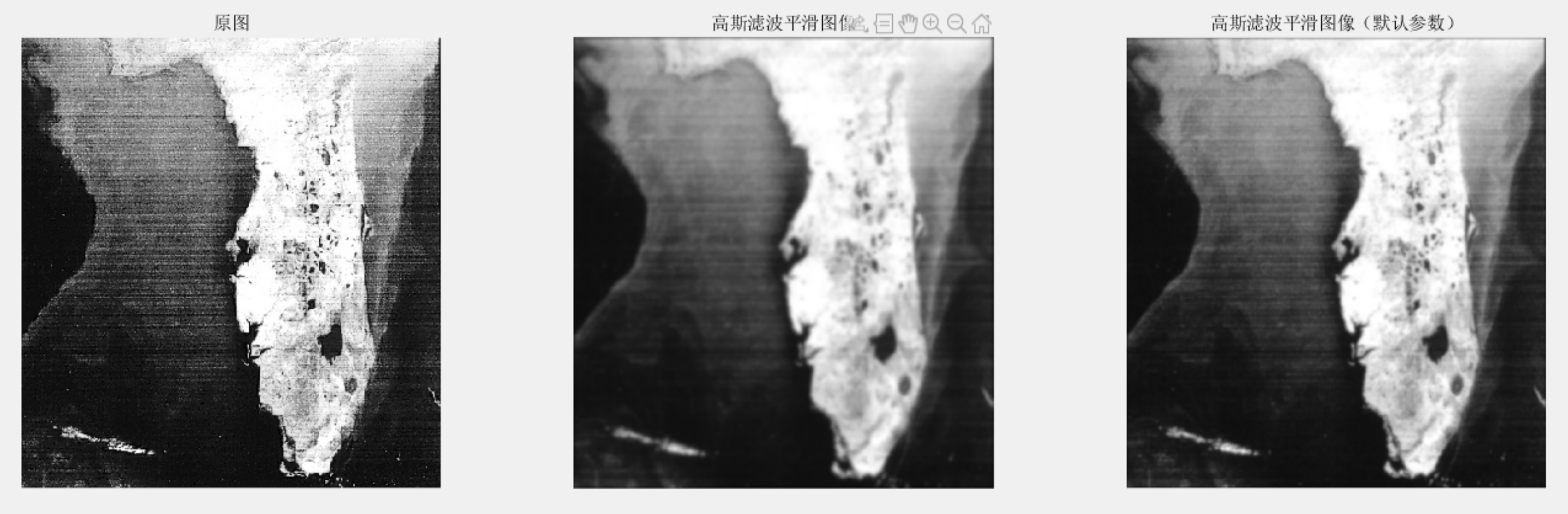
- $D_0=100$,滤波器大小为原图像两倍,滤波器中心为图像的中心

验证正确性。
- $D_0=100$,滤波器大小为原图像
1200 x 1200,滤波器中心为(600,600)

比较滤波器大小的影响:滤波器窗口大小不同,处理的图像分辨率不一样。窗口大看到的分辨率小,窗口小看到分辨率大。所以窗口大就会导致细节丢失,而窗口小会留下细节,但是噪声也会被误认为细节。所以发现,中间的图像平滑度并没有后者高。
- $D_0=80(middle),D_0=120(right)$,滤波器大小为原图像两倍,滤波器中心为图像的中心
比较截止频率:当信号频率低于这个截止频率时,信号得以通过;当信号频率高于这个截止频率时,信号输出将被大幅衰减。这个截止频率即被定义为通带和阻带的界限。也就是说,截止频率越低,平滑效果更好。
Innovation points
实现更加规范化,也更具有通用性。
通过设置不同的参数,比较得到滤波器大小和截止频率的意义。
Appendix
高斯低通滤波器
function [g] = GaussianLowPassFilter(f, D0, P, Q, u0, v0)
% 高斯低通滤波器
% f 是输入图像
% D0 是截止频率
% P 和 Q 是滤波器的大小
% u0 和 v0 是滤波器的中心
% 1.给定一幅大小为 M x N 的输入图像f(x,y),得到填充参数 P 和 Q
% 这里的缺省参数是P = 2M, Q = 2N, u0 = P / 2, v0 = Q / 2
[m,n] = size(f);
f = mat2gray(f, [0 255]);
if nargin == 2
P = 2 * m;
Q = 2 * n;
u0 = P / 2;
v0 = Q / 2;
end
% 2.对f(x, y)添加必要数量的0,形成大小为P x Q的填充后的图像fp(x, y)
fp = zeros(P, Q);
fp(1 : m, 1 : n) = f(1 : m, 1 : n);
% 3.用(-1)^[2 * (u0 * x / P + v0 * y / Q)]乘以fp(x, y)移到(u0, v0)
cx = 2 * u0 / P;
cy = 2 * v0 / Q;
for x = 1 : m
for y = 1 : n
fp(x, y) = double(fp(x, y) * (-1) ^ (cx * x + cy * y));
end
end
% 4.计算来自步骤3的图像的DFT,得到F(u,v)
F = fft2(fp, P, Q);
% 5.生成一个实的、对称的滤波函数H(u, v),其大小为P x Q,中心在(u0, v0)处
% 用阵列相乘形成乘积G(u, v) = H(u, v)F(u, v);即G(i, k) = H(i, k)F(i, k)
H = zeros(P, Q);
for u = 1 : P
for v = 1 : Q
D = (u - u0) ^ 2 + (v - v0) ^ 2;
H(u, v) = exp((-D) / (2 * D0 ^ 2));
end
end
G = H .* F;
% 6.得到处理后的图像
gp = ifft2(G);
gp = real(gp);
for x = 1 : m
for y = 1 : n
gp(x, y) = double(gp(x, y) * (-1) ^ (cx * x + cy * y));
end
end
% 7.通过从gp(x,y)的左上象限提取 M * N 区域,得到最终处理结果g(x,y)
g(1 : m, 1 : n) = gp(1 : m, 1 : n);
主函数
f = imread("another.tif");
g = GaussianLowPassFilter(f, 100, 1570, 1464, 785, 732);
h = GaussianLowPassFilter(f, 100);
figure
subplot(1, 3, 1)
imshow(f)
title('原图')
subplot(1, 3, 2)
imshow(g)
title('高斯滤波平滑图像')
subplot(1, 3, 3)
imshow(h)
title('高斯滤波平滑图像(默认参数)')