自然语言处理

NLP的一些问题

自然语言处理

Posted by Birdie on May 2, 2022

Lecture 1: Introduction

掌握

自然语言处理(NLP)的概念、挑战、常见应用

概念：

NLP 是一门通过可计算的方法研究转换、分析、处理和“理解”自然语言的学科，是计算机科学和语言学的交叉学科。

挑战：

  1. 歧义（词汇歧义，词性歧义，结构歧义）
  2. 未知的语言现象（新的术语人名地名，旧词新用，新的语言用法）

应用：

人机交互（计算机回答系统）、搜索引擎、机器翻译、信息提取和推理、文本生成、知识图谱、生成摘要、情感分析

文本预处理(text processing)的步骤和方法

步骤：

tokenizing words（分词）

方法：

有监督学习的序列模型，得到 subword 标记

  1. 字节对编码（有一个结束标记space）

image-20220103063301325

  1. unigram语言模型标记

    $P(w_1w_2…w_n)=\Pi_iP(w_i)$

  2. wordpiece

步骤：

normalizing word（合并大小写，统一时态语态，提取词根）

方法：

人为定义规则

步骤：

Sentence Segmentation（分句）

方法：

采用基于规则的方法

机器学习的方式学习一个分类器

了解

自然语言处理和人工智能及机器学习的关系

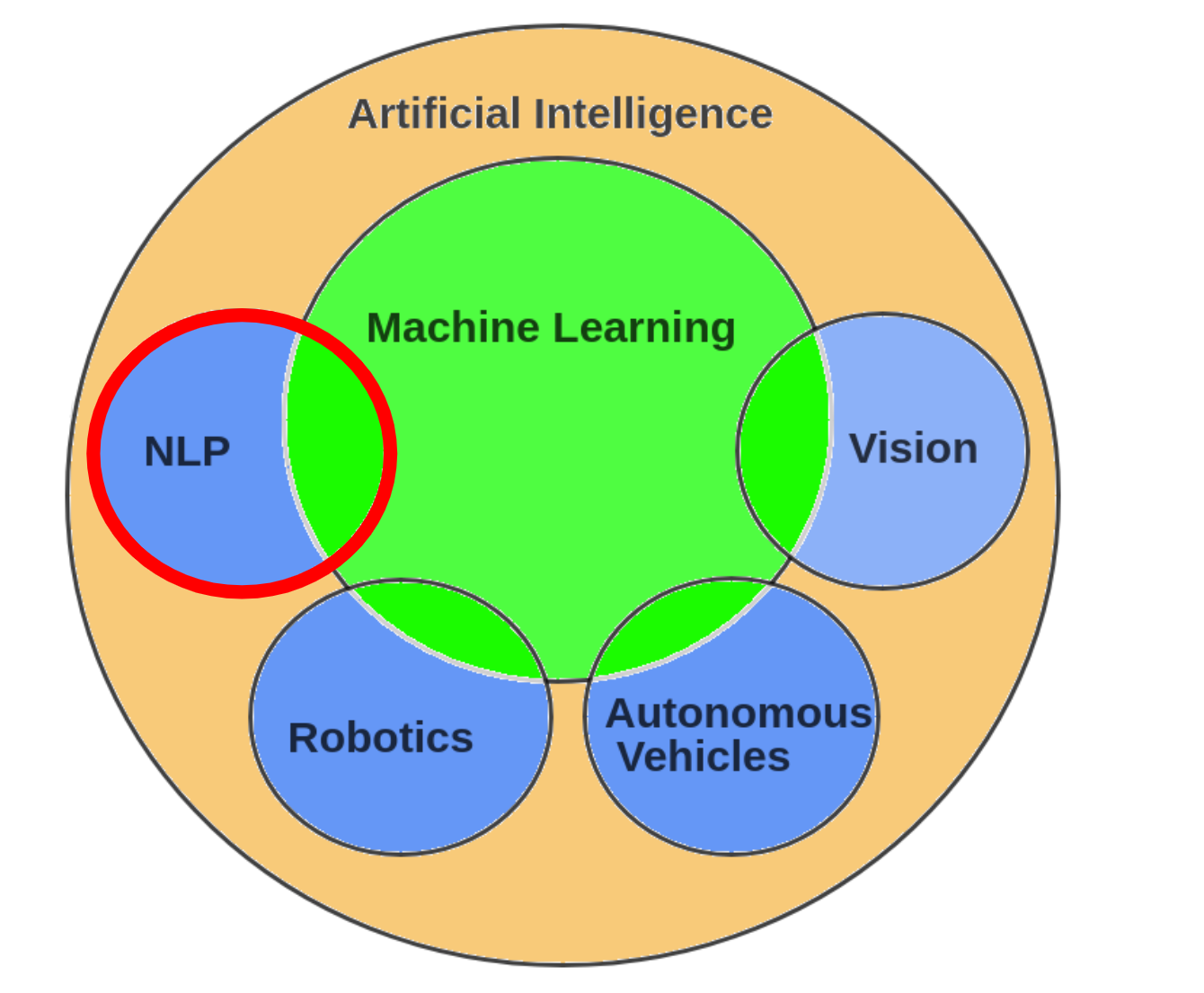
image-20220103062424852

自然语言处理的不同发展阶段

  • 第一阶段(地上爬)：统计机器学习为代表
  • 第二阶段(爬上第一阶梯)：word2vec为代表
  • 第三阶段(爬上第二阶梯)：bert为代表（2018）

Lecture 2: N-gram Language Model

掌握

语言模型(language model)的概念和目的

概念：

计算给定历史的序列中下一个单词的概率

$P(W) $ or $P(w_n w_1,w_2,…,w_{n-1})$

目的：

计算一个句子或单词序列的概率$P(W) = P(w_1,w_2,w_3,w_4,w_5,…,w_n)$

基于n-gram和极大似然估计的语言模型计算方法

n-gram

\[P(w_i|w_1,w_2,...,w_{i-1})\approx P(w_i|w_{i-n+1},w_{i-n+2},...,w_{i-1})\] \[P(w_1w_2...w_n)=\Pi_iP(w_i)\]

极大似然估计

\[P(w_i|w_{i-1})=\frac{\text{count}(w_{i-1},w_i)}{\text{count}(w_{i-1})}\]

了解

语言模型的评估(evaluation)

两个模型 A 和 B，放进一个任务，执行任务（预测下一个词语），比较准确度

比较逆频率perplexity，用词数归一化

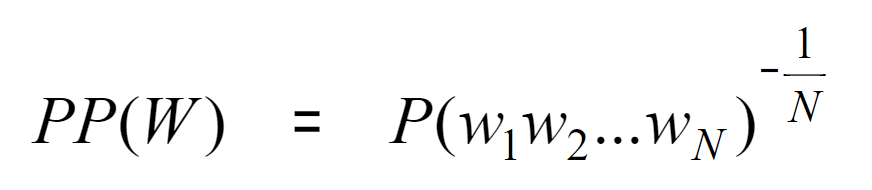
image-20220103065508174

谁更低模型更好

语言模型的平滑(smoothing)

前者最大似然估计，后者拉普拉斯平滑，防止概率为0

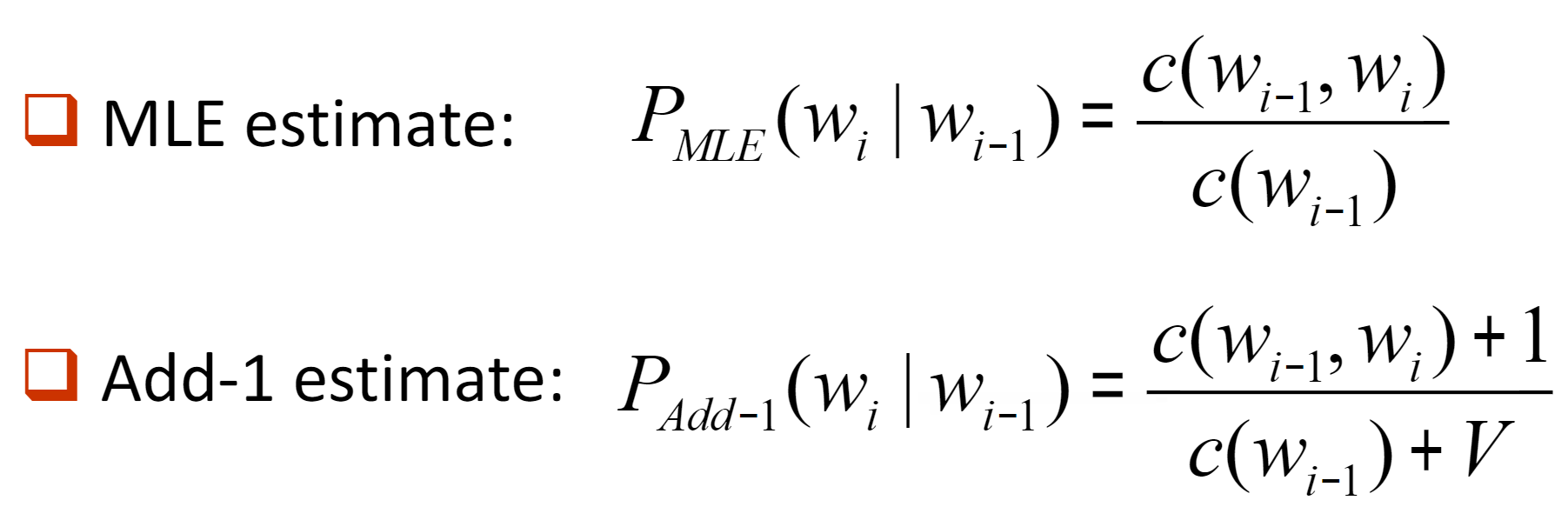
image-20220103065935427

Lecture 3: Text Classification

掌握

文本分类(text classification)任务的定义和意义

定义：

​ 输入

  • 文章$d$
  • 一个集合的类别$C={c_1,…,c_j}$

​ 输出：一个预测分类$c\in C$

意义：

​ 情感分析、垃圾邮件检测、作者身份识别、语言识别、类别主题流派分类

朴素贝叶斯分类器(Naive Bayes Classifier)的原理与训练方法

原理：

\[\begin{aligned} c_{M A P} &=\underset{c \in C}{\operatorname{argmax}} P(c \mid d) \\ &=\underset{c \in C}{\operatorname{argmax}} \frac{P(d \mid c) P(c)}{P(d)} \\ &=\underset{c \in C}{\operatorname{argmax}} P(d \mid c) P(c) \\ &=\underset{c \in C}{\operatorname{argmax}} P(x_1,x_2,...,x_n \mid c) P(c) \end{aligned}\]

$P(c)$是训练集中类别$c$出现的概率

\[P\left(x_{1}, \ldots, x_{n} \mid c\right)=P\left(x_{1} \mid c\right) P\left(x_{2} \mid c\right) P\left(x_{3} \mid c\right) \ldots P\left(x_{n} \mid c\right)\]

即

\[c_{N B}=\underset{c \in C}{\operatorname{argmax}} P\left(c_{j}\right) \prod_{x_{i} \in X} P\left(x_{i} \mid c\right)\]

而连乘会导致精度爆炸，两边取log

\[c_{\mathrm{NB}}=\underset{c_{j} \in C}{\operatorname{argmax}}\left[\log P\left(c_{j}\right)+\sum_{i \in \text { positions }} \log P\left(x_{i} \mid c_{j}\right)\right]\]

训练方法：

监督机器学习

输入：

  • 文章$d$
  • 一个集合的类别$C={c_1,…,c_j}$
  • $m$个手动标签的数据集$(d_1,c_1)…(d_m,c_m)$

输出：学习到的分类器$f:d\to c$

平滑

在最大似然估计的方法下，防止概率为0，做拉普拉斯平滑

\[\begin{aligned} \hat{P}\left(w_{i} \mid c\right) &=\frac{\operatorname{count}\left(w_{i}, c\right)+1}{\sum_{w \in V}(\operatorname{count}(w, c)+1)} \\ &=\frac{\operatorname{count}\left(w_{i}, c\right)+1}{\left(\sum_{w \in V} \operatorname{count}(w, c)\right)+|V|} \end{aligned}\]

未知词

对于出现在测试集中但不出现在训练集中的词语，我们将其忽略

停用词

出现频率非常高的词语

按照频率排序，取频率最高的10到50个词语为停用词，删除

但是停用词不影响朴素贝叶斯算法

了解

基于朴素贝叶斯实现情感分析(sentiment analysis)

词语出现比词语频率更重要

将词语出现的次数固定为1，使用二值朴素贝叶斯

Lecture 4: Vector Semantics & Embeddings (I)

掌握

词向量的动机与意义

动机：

  • 对于训练中未出现过的词语，传统方法无法进行预测

  • 得到词语之间的相似度，可以生成相似的未出现过的词语

意义：

词向量能够在计算机中表示，同时能够表征词语之间的关系。

用TF-IDF获取词向量和文本向量的方法

假设词语为$t$，文档为$d$：

总计算式：$w_{t,d}=tf_{t,d}\times idf_t$

词频率：$tf_{t,d}=count(t,d)$

实际计算：$tf_{t,d}=\text{log}_{10}(count(t,d)+1)$

$df_t$是$t$出现的文档数

$idf_t=log_{10}\frac{N}{df_t}$

基于TF-IDF计算词语/文本相似度的方法

计算两个TF-IDF的：

  • 点积（越大越相似）

  • cos（1相似，-1相反，0正交）

比较相似性。

了解

词义(word meaning)

一词多义，同义词，词语的相似性，词语的相关性，反义词，语境，词语的情感色彩

警觉度（高兴程度）、唤醒度（强度）、支配度（控制度）

signifier (symbol) <=> signified (idea or thing)

词义的想法是把 meaning 视为事物的代表

基于互信息(mutual information)获取词向量的方法

\[PMI(w_1,w_2)=log\frac{p(w_1,w_2)}{p(w_1)p(w_2)}\] \[\operatorname{PPMI}\left(\text { word }_{1}, \text { word }_{2}\right)=\max \left(\log _{2} \frac{P\left(\text { word }_{1}, \text { word }_{2}\right)}{P\left(\text { word }_{1}\right) P\left(\text { word }_{2}\right)}, 0\right)\]

image-20220104162642183

Lecture 5: Vector Semantics & Embeddings (II)

掌握

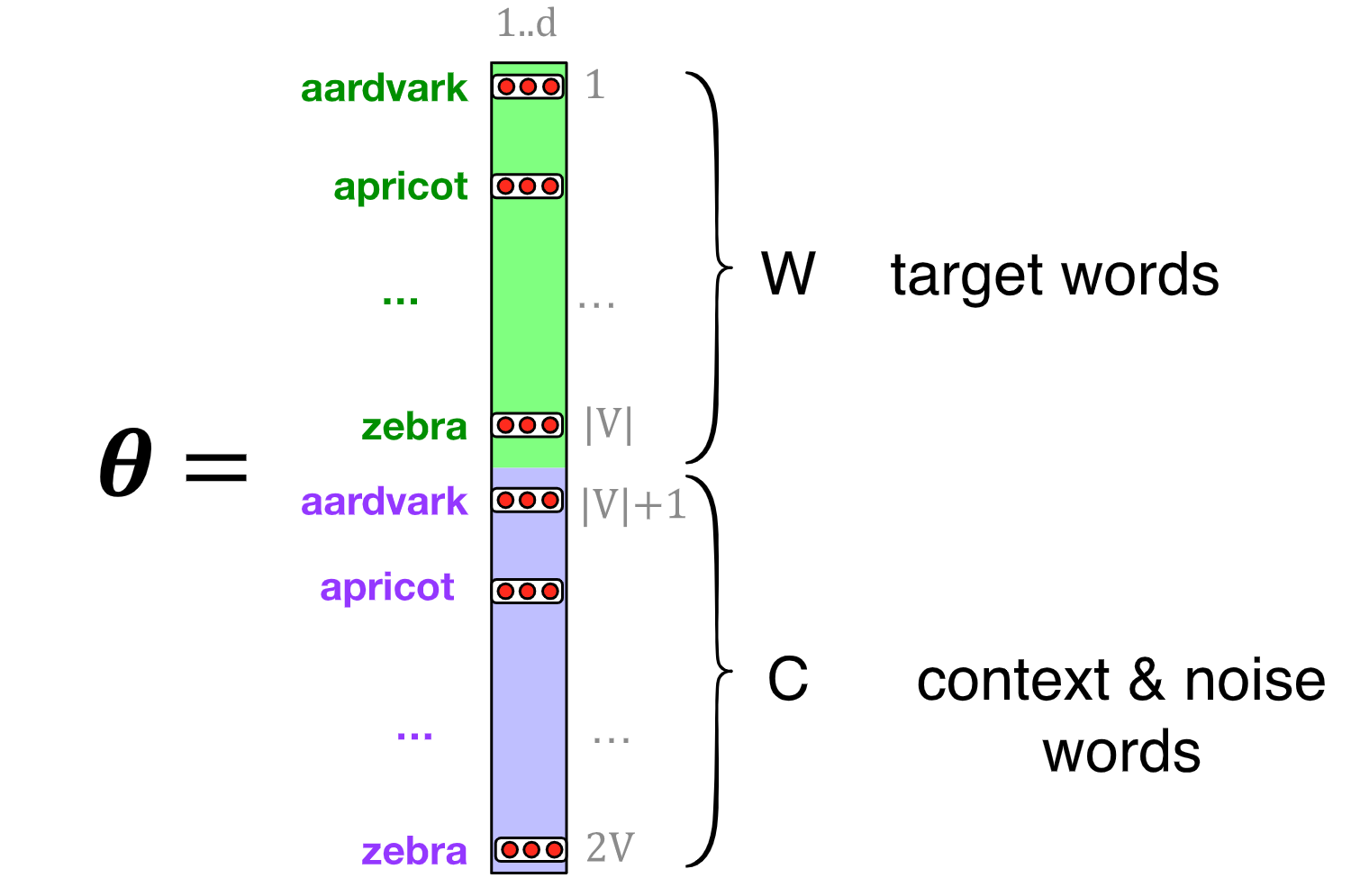
Word2Vec模型计算词向量的原理

思想：采用预测而不是计数

训练一个二值预测任务上的分类器（词语是否在bank的附近），但是不关心任务本身，只需要学习到的分类器的权重作为词向量

核心思想是采用自监督的方式，将词语出现在bank附近作为监督学习的答案，不需要人工标记

  1. 将目标词 t 和相邻的上下文词 c 视为正样本。
  2. 随机采样词典中的其他词语作为负样本。
  3. 训练一个逻辑回归分类器用于分辨两种样本。
  4. 使用学习到的权重作为词向量。

完成后，两个词语的相似度正比于两个向量的点积

Word2Vec模型的训练方法

给定一组正负训练实例（取一个语料库，将同时出现的词对作为正例；将不同时出现的词对作为反例；），以及一组初始嵌入向量。

学习的目标是调整这些词向量，使得我们：

  • 最大化目标词的相似度，从正数据中提取的上下文词对$(w, c_{pos})$
  • 最小化从负数据中提取的$(w, c_{neg})$对的相似性。

损失函数，采用随机梯度下降

\[\begin{aligned} L_{\mathrm{CE}} &=-\log \left[P\left(+\mid w, c_{\text {pos }}\right) \prod_{i=1}^{k} P\left(-\mid w, c_{\text {neg }_{i}}\right)\right] \\ &=-\left[\log P\left(+\mid w, c_{\text {pos }}\right)+\sum_{i=1}^{k} \log P\left(-\mid w, c_{\text {neg }_{i}}\right)\right] \\ &=-\left[\log P\left(+\mid w, c_{\text {pos }}\right)+\sum_{i=1}^{k} \log \left(1-P\left(+\mid w, c_{\text {neg }_{i}}\right)\right)\right] \\ &=-\left[\log \sigma\left(c_{\text {pos }} \cdot w\right)+\sum_{i=1}^{k} \log \sigma\left(-c_{\text {neg }_{i}} \cdot w\right)\right] \end{aligned}\]

更新方法为

\[\begin{aligned} c_{\text {pos }}^{t+1} &=c_{\text {pos }}^{t}-\eta\left[\sigma\left(c_{\text {pos }}^{t} \cdot w^{t}\right)-1\right] w^{t} \\ c_{\text {neg }}^{t+1} &=c_{\text {neg }}^{t}-\eta\left[\sigma\left(c_{\text {neg }}^{t} \cdot w^{t}\right)\right] w^{t} \\ w^{t+1} &=w^{t}-\eta\left[\left[\sigma\left(c_{\text {pos }} \cdot w^{t}\right)-1\right] c_{\text {pos }}+\sum_{i=1}^{k}\left[\sigma\left(c_{\text {neg }_{i}} \cdot w^{t}\right)\right] c_{\text {neg }_{i}}\right] \end{aligned}\]

最后结果$w_i+c_i$

Word2Vec中负采样(negative sampling)的原理和目的

原理：

随机采样词典中的其他词语作为负样本，训练分类器分辨无关词语的能力。

目的：

  1. 在随机梯度下降中

    • 第一个问题，我们每次只对窗口中出现的几个单词进行升级，但是在计算梯度的过程中，我们是对整个参数矩阵进行运算，这样参数矩阵中的大部分值都是0。
    • $\operatorname{softmax}\left(u_{o}^{T} v_{c}\right)=p(o \mid c)=\hat{y}{o}=\frac{e^{u{o}^{T} v_{c}}}{\sum_{w=1}^{W} e^{u_{w}^{T} v_{c}}}$，分母需要把窗口中所有单词的“得分”都算出来再求和，效率低下

    因此，采用负采样可以解决这两个问题：仅对K个参数进行采样，且用sigmoid代替softmax

  2. 保证了模型训练的效果，其一模型每次只需要更新采样的词的权重，不用更新所有的权重，那样会很慢，其二中心词其实只跟它周围的词有关系，位置离着很远的词没有关系，也没必要同时训练更新

了解

词向量的属性(properties)

  1. 平行四边形的类比关系

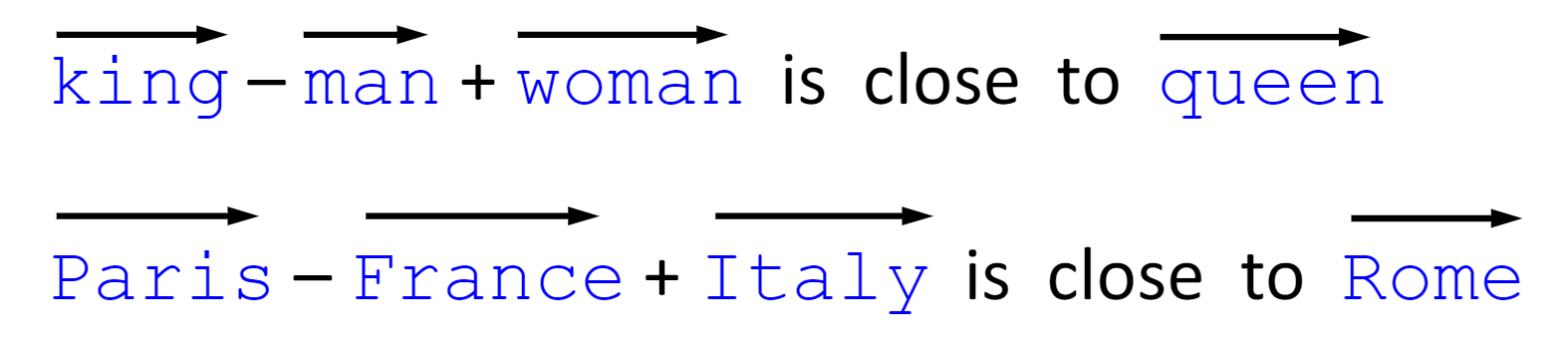
image-20220105215128177

  1. 随着时间的推移变化

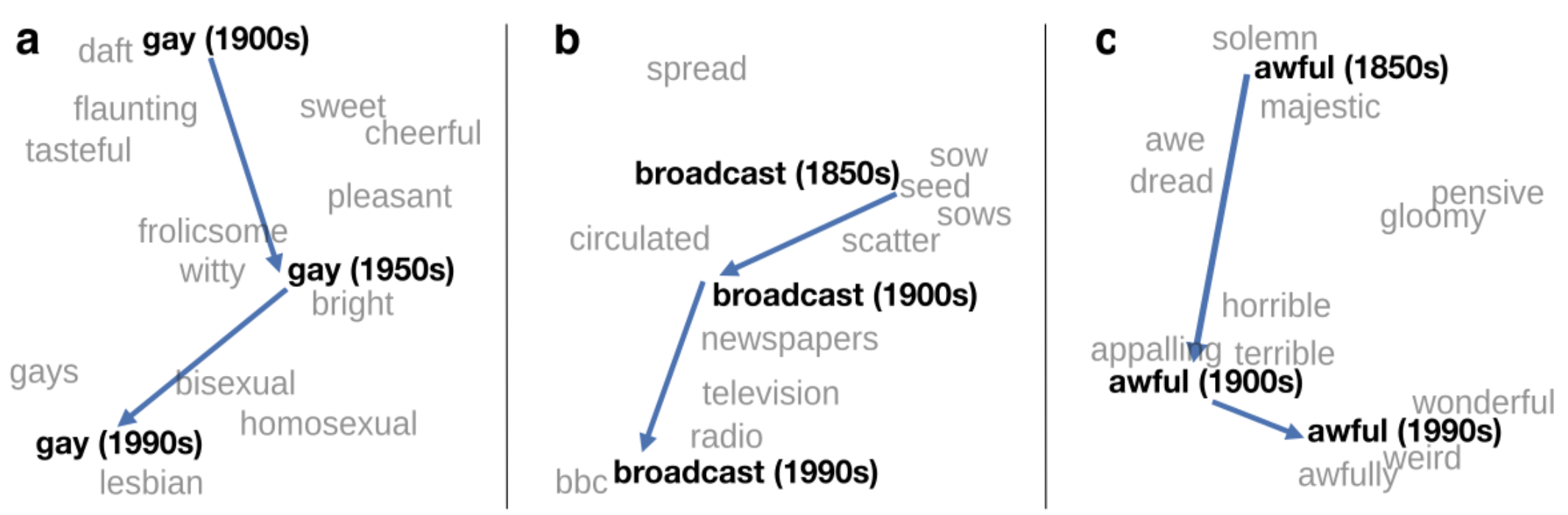
image-20220105215410536

  1. 反应了文化关系

image-20220105215438252

Word2Vec中skip-gram的原理

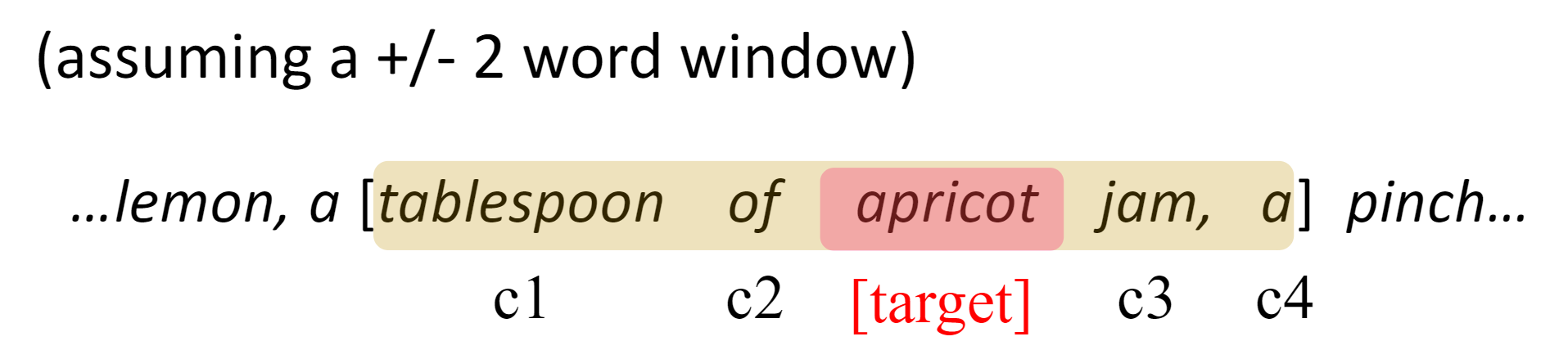
image-20220105211910517

目标是训练一个分类器对于给定的pair：(target, c)

然后计算每一个pair的概率

\[P(+|w,c)\\ P(-|w,c)=1-P(+|w,c)\]

由于两个词语的相似度正比于点积，我们将使用逻辑回归中的 sigmoid 将其转换为概率

\[\begin{aligned} P(+\mid w, c) &=\sigma(c \cdot w)=\frac{1}{1+\exp (-c \cdot w)} \\ P(-\mid w, c) &=1-P(+\mid w, c) \\ &=\sigma(-c \cdot w)=\frac{1}{1+\exp (c \cdot w)} \end{aligned}\]

对于一个中心词，有若干个上下文(context word)

\[\begin{aligned} P\left(+\mid w, c_{1: L}\right) &=\prod_{i=1}^{L} \sigma\left(c_{i} \cdot w\right) \\ \log P\left(+\mid w, c_{1: L}\right) &=\sum_{i=1}^{L} \log \sigma\left(c_{i} \cdot w\right) \end{aligned}\]

总结，对于中心词w和上下文窗口中的词语列表c，通过词向量计算相似度，对于所有的词语都算一遍。

image-20220105213003854

Lecture 6: Neural Language Modeling

掌握

如何通过神经网络计算语言模型

输入采用滑动窗口（n-gram），网络输出一个词典大小的向量，代表预测该词语的条件概率。

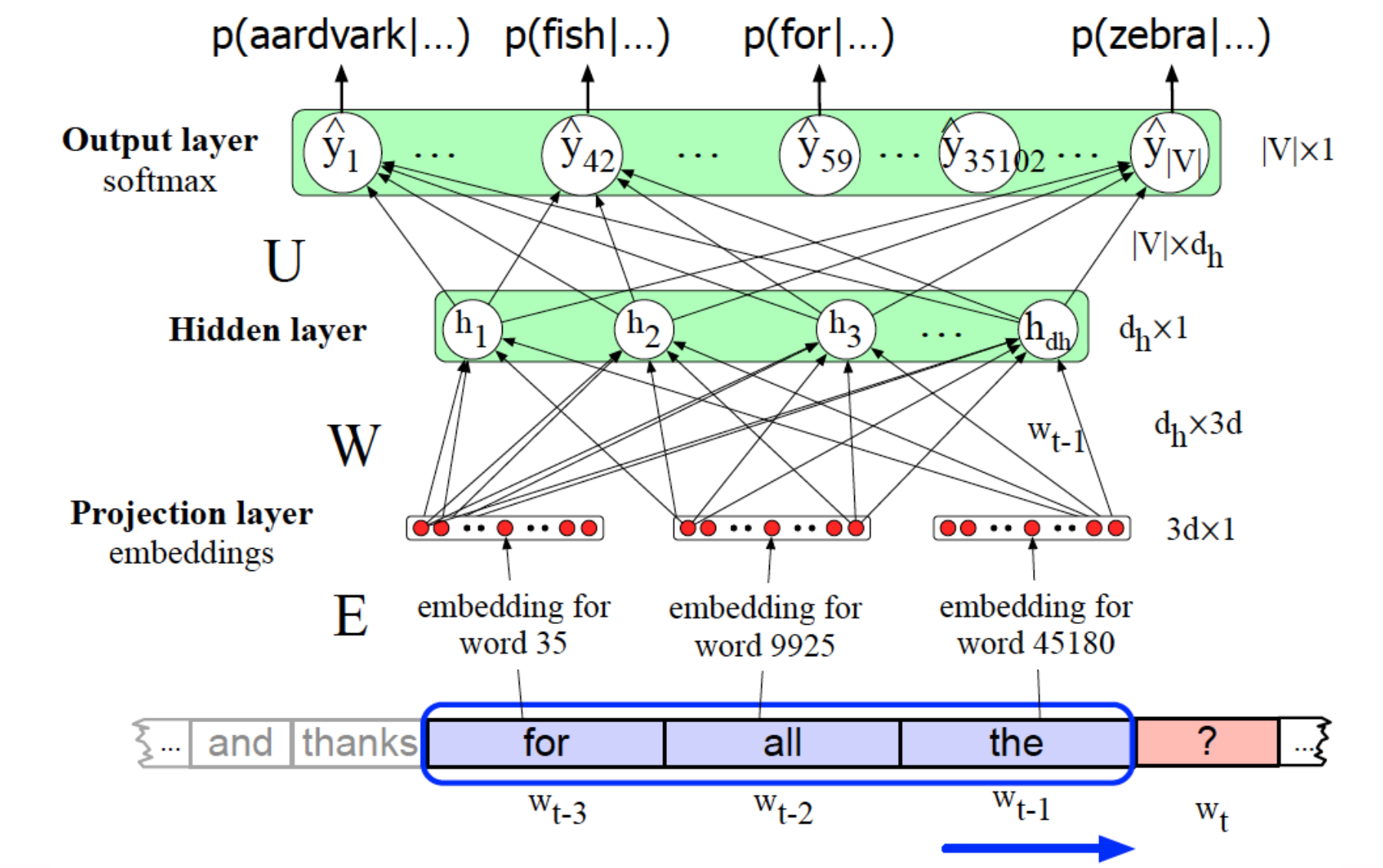
image-20220105220813822

相比n-gram，神经语言模型的优势

  • 深度学习的真正力量来自于从数据中学习特征的能力，而不是使用人工设计的特征进行分类
  • 神经网络模型可以使用词向量之间的相似性来概括和预测句子，而n-gram在训练集中未出现的词组无法进行预测

了解

计算图(computation graphs)

计算图表示计算数学表达式的过程。

由于损失仅在网络的最末端计算，给定一个计算图和其中所有函数的导数，我们可以自动计算损失相对于这些早期权重的导数。

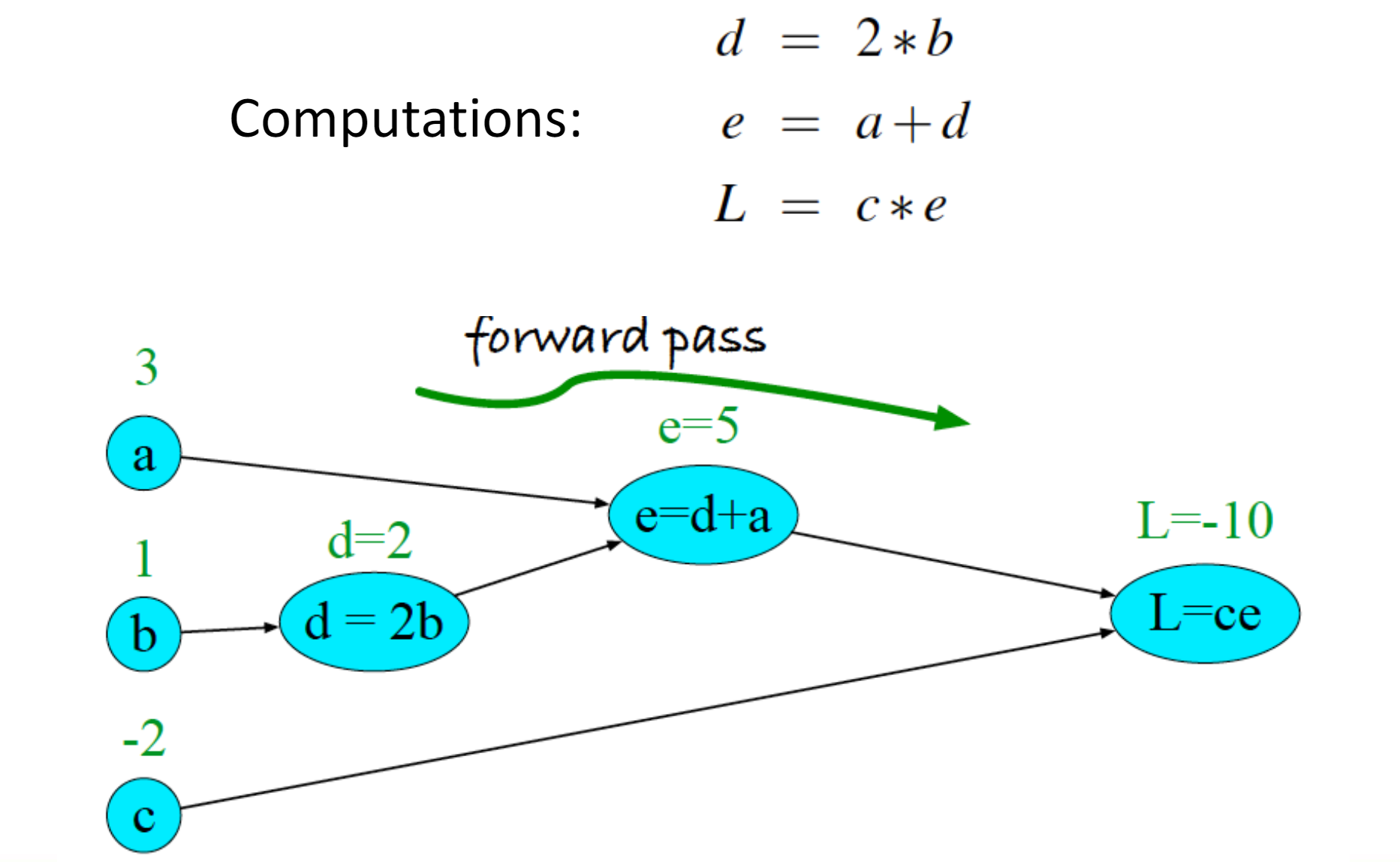
image-20220105221457889

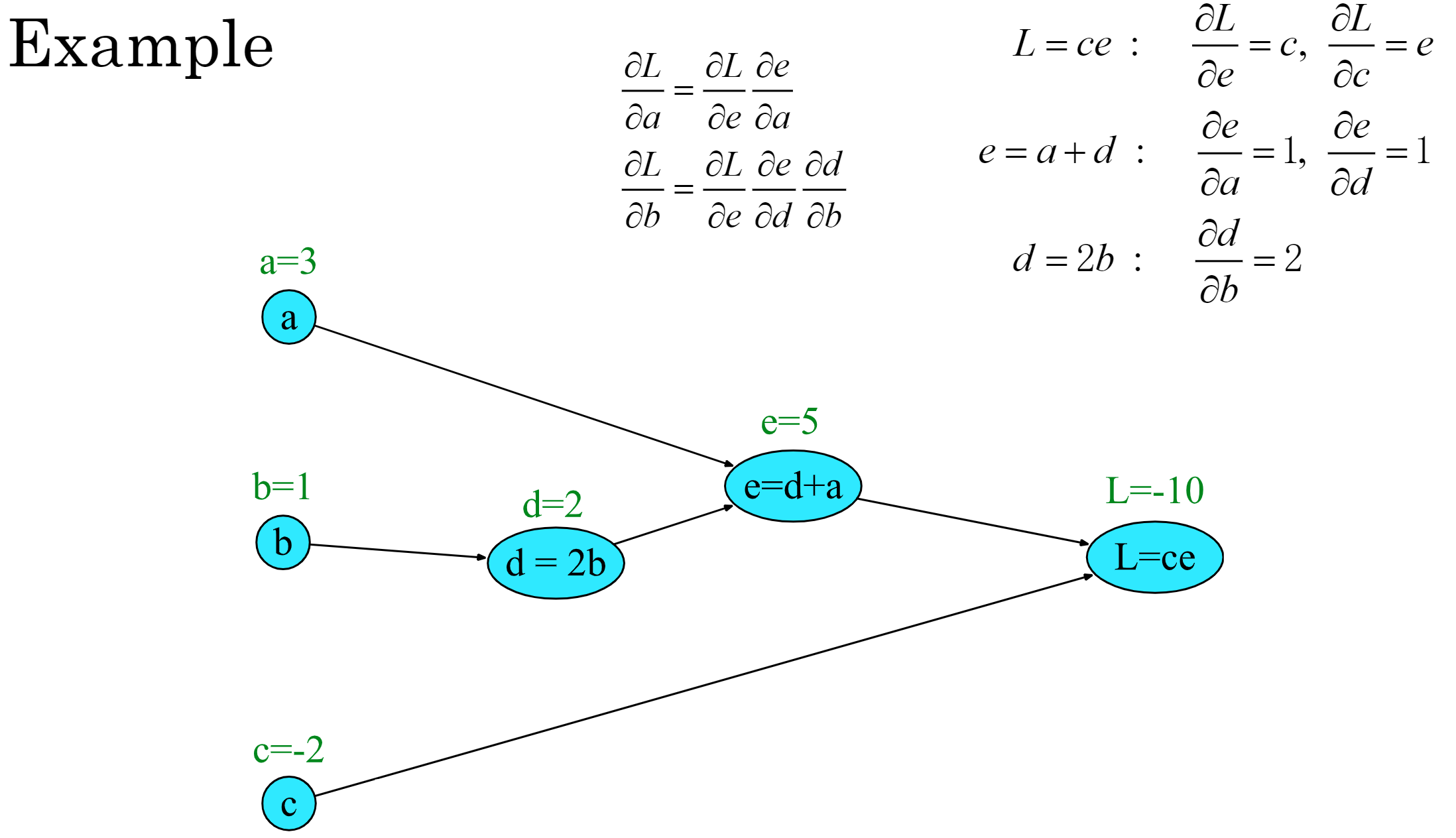
image-20220105221617513

反向微分(backward differentiation)

损失函数

\[\begin{aligned} L_{\mathrm{CE}}(\hat{y}, y) &=-\log p(y \mid x)=-[y \log \hat{y}+(1-y) \log (1-\hat{y})] \\ &=-[y \log \sigma(w \cdot x+b)+(1-y) \log (1-\sigma(w \cdot x+b))] \end{aligned}\]

image-20220105221212270

image-20220105221337465

Lecture 7: Part of Speech and Named Entities

掌握

什么是词性标注(Part of Speech tagging)及意义

概念

注释句子中的每个单词的词性。

  • colsed class 类别由给定语言的一组固定的小的语法功能词组成。
  • open class 类别有大量的单词，很容易发明新的。

意义

对很多NLP任务有用：

  • 解析：词性标注可以改进句法解析
  • 机器翻译：形容词和名词的重新排序（比如从西班牙语到英语）
  • 情感任务：可能想要区分形容词或其他词性
  • 文本到语音（我们如何发音“lead”或“object”？）

或语言或语言分析计算任务

  • 在研究语言变化时需要控制词性，比如创造新词，或者意义转移
  • 或在测量意义相似性或差异时

什么是命名实体识别(Named Entity tagging)及意义

概念

命名实体在其核心用法中是指可以用专有名称引用的任何事物。

最常见的4个标签：人、地点、组织机构、地缘政治实体。

通常是多词短语。

可扩展到非实体：日期、时间、价格等。

意义

  • 情感分析：消费者对特定公司或个人的情绪？
  • 问答：回答有关实体的问题？
  • 信息提取：从文本中提取有关实体的事实。

了解

如何实现词性标注

通常假设一个单独的初始标记化过程来分离和/或消除标点符号的歧义，包括检测句子边界。

监督机器学习：

  • Hidden Markov Models
  • Conditional Random Fields
  • Neural sequence models
  • Large Language Models 微调

所有这些都需要一个手工标记的训练集。

如何实现命名实体识别

采用BIO标记：

  • B 词组开头

  • I 词组内部

  • O 不属于词组

具体方法同词性标注。

Lecture 8: Constituency Parsing

掌握

什么是句法结构(syntax structure)

句法结构指的是词与词之间相互联系、相互作用的方式。

一个具体的句法结构通常称为一个结构体。

什么是成分句法(constituency structure)

短语结构语法，表示句子的成分（即主语谓语宾语等）。

基于上下午无关文法

  1. 词性标注
  2. 单词组合成带有类别的短语
  3. 短语可以递归组合成更大的短语

（成分）句法解析是识别句子并为其分配（成分）结构的任务。

什么是上下文无关文法(context-free grammars)及作用

概念：

上下文无关文法取名为“上下文无关”的原因就是因为字符 V 总可以被字串 w 自由替换，而无需考虑字符 V 出现的上下文。 一个形式语言是上下文无关的，如果它是由上下文无关文法生成的（条目 上下文无关语言 ）。

image-20220108171710255

作用：

用于成分句法的最广泛使用的形式系统。

构建出语法分析树，用于成分句法。

概率上下文无关文法(Probabilistic Context-free Grammar)的意义

R 中每一条边都有概率。

image-20220108172459243

提高了上下文无关文法的准确性，一定程度上解决了上下文无关文法无法纠错的缺点。

了解

如何得到概率上下文无关文法中每条规则(rule)的概率

有一个treebank，即规则（树边）库。

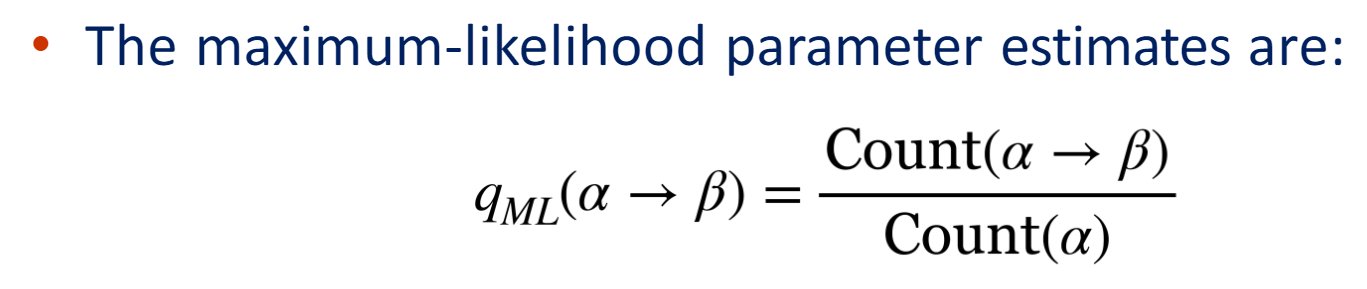
image-20220108172923838

如何计算整棵成分句法树的概率

对于所有树边，求其概率的乘积，选择概率最高的解析。

CKY算法和词汇化概率上下文无关文法(Lexicalized PCFGs)

CKY算法

使用兄弟树将tree变成二叉树

在树上进行区间动态规划：

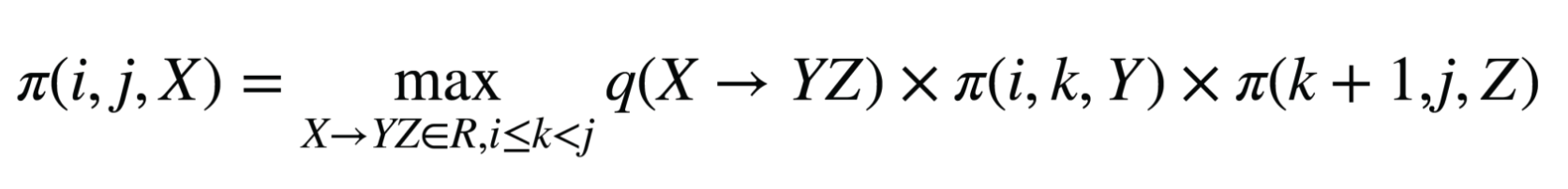
image-20220108173123763

词汇化概率上下文无关文法

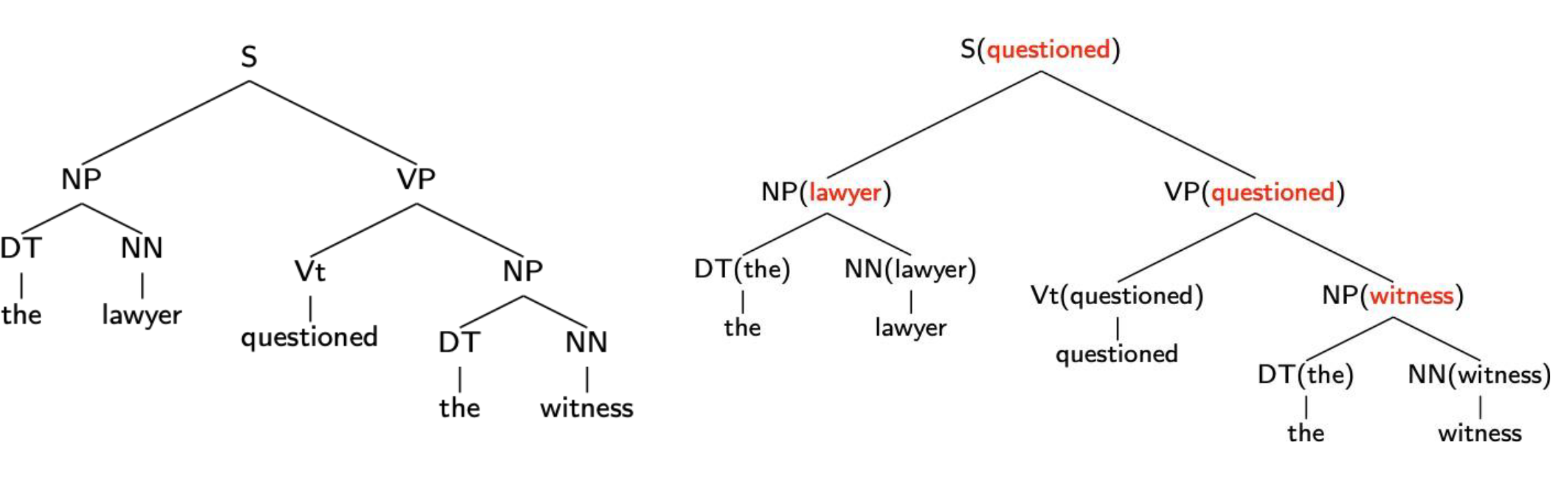
核心思想：给树结点增加词条。

每个上下文无关规则都有一个特殊的子节点，它是规则的头部（语法中的核心思想）。

image-20220108173425775

Lecture 9: Constituency Parsing

掌握

什么是依存句法解析(dependency parsing)

依存分析仅根据单词和一组相关联的、在这些单词之间保持的与头部相关的语法关系来描述句子的句法结构。

  • 有且只有一个词语(ROOT，虚拟根节点，简称虚根)不依存于其他词语。
  • 除此之外所有单词必须依存于其他单词。
  • 每个单词不能依存于多个单词。
  • 如果单词 A 依存于 B，那么位置处于 A 和 B 之间的单词 C 只能依存于 A、B 或 AB 之间的单词。

依存句法(dependency structure)和成分句法(constituency structure)的区别

依存句法分析更多的是关注句子中单词之间的依存关系，而成分句法分析则是将句子拆解为更小的部分 (短语)进行理解。

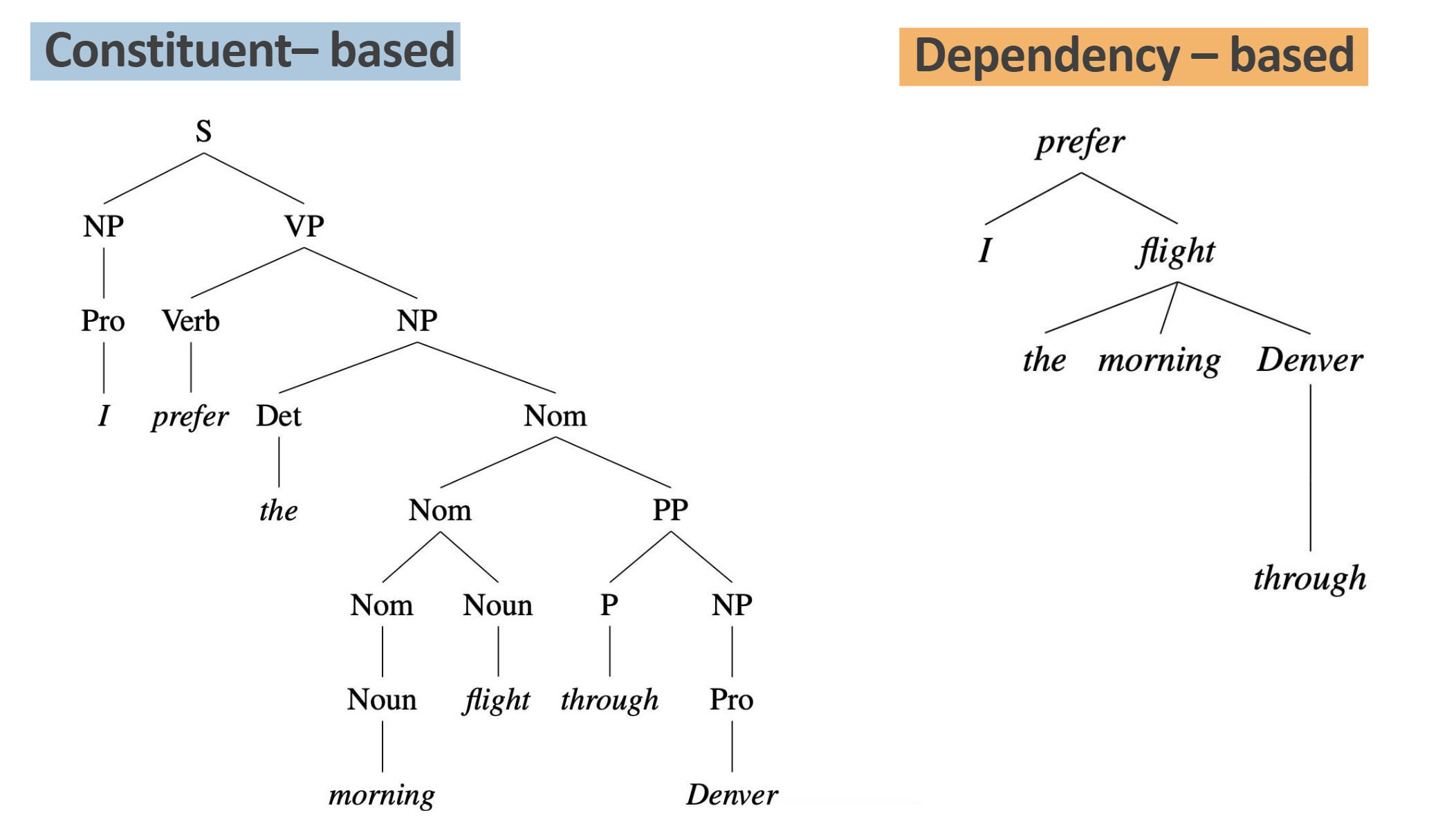
image-20220109144055466

相比成分句法，依存句法有什么优势

  • 依存关系没有对应于短语成分的节点。相反，它们直接编码通常隐藏在短语结构解析中的信息。

  • 依赖解析能够更好地处理具有相对自由词序的语言。

  • 依赖关系近似于单词和参数之间的语义关系，这对于许多应用程序很有用

    • 问答
    • 信息提取

了解

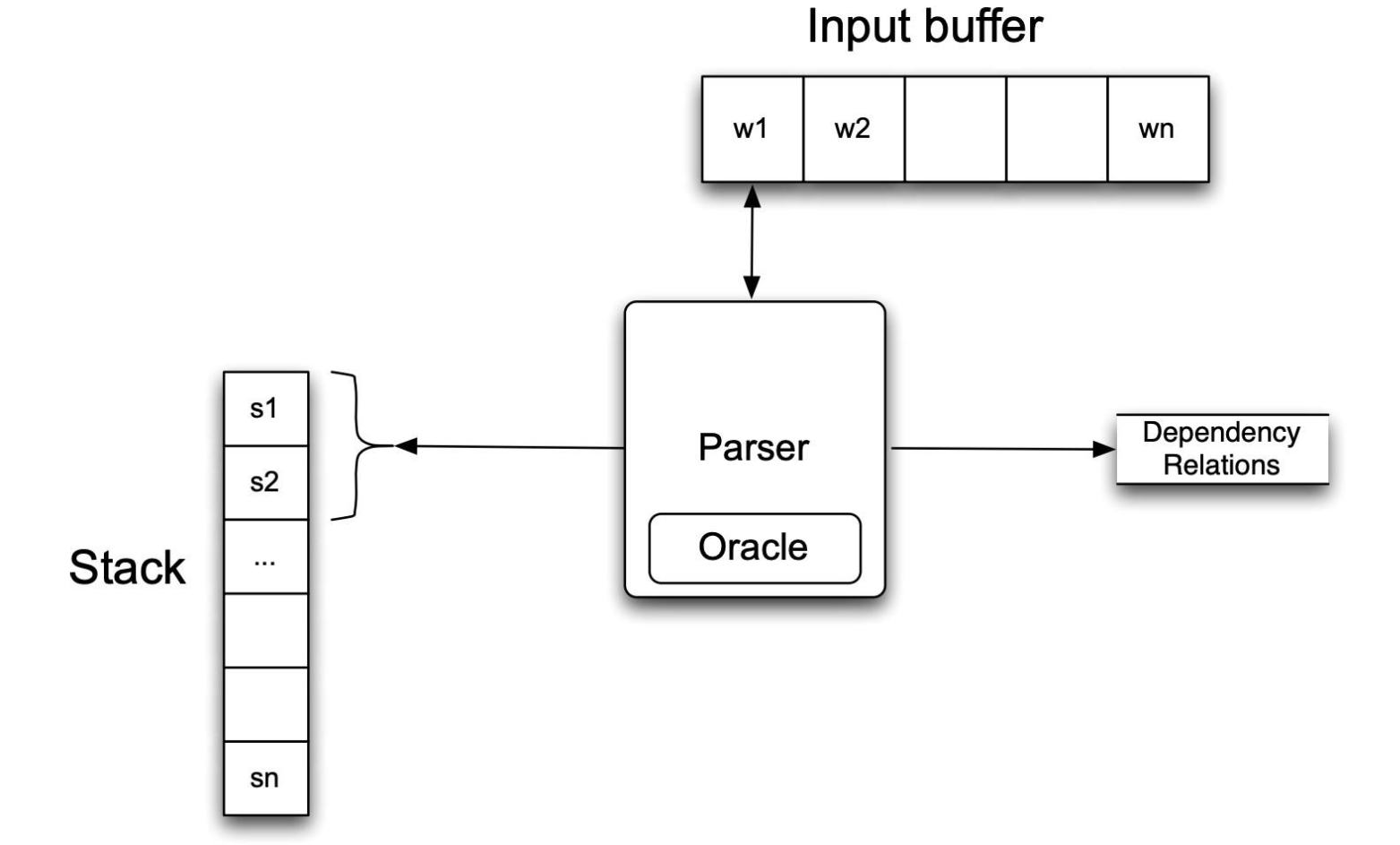
Transition-Based依存句法解析方法

思想：贪心。

基于转换的解析中的一个关键元素是配置的概念，它由堆栈、单词的输入缓冲区和一组表示依赖树的关系组成。

image-20220109145103884

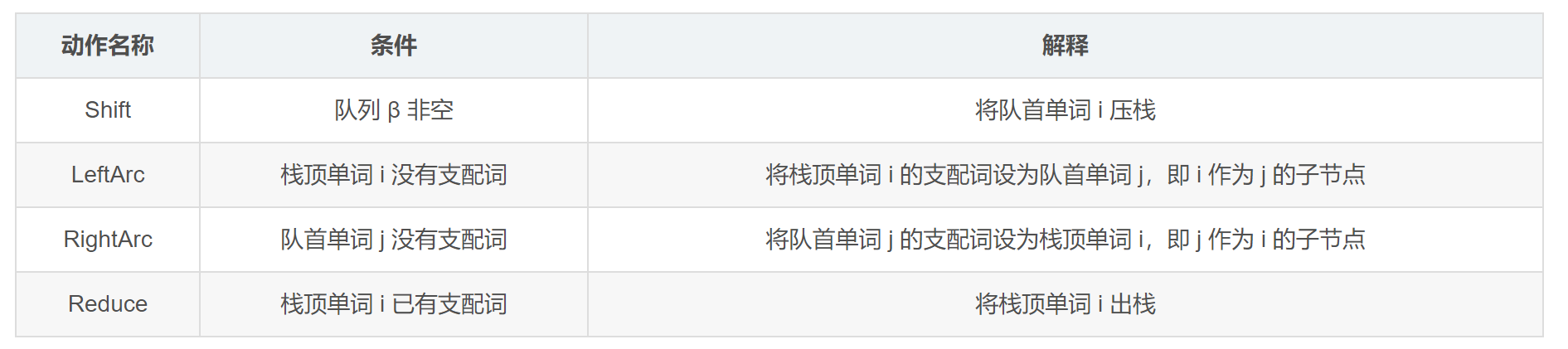
image-20220109145138957

采用有监督的机器学习。

训练数据：通过运行算法来模拟解析器的操作，并依靠新的训练预言机为每个连续操作提供正确的转换运算符。

训练过程：

  1. leftarc是对的就leftarc
  2. 否则rightarc是对的就rightarc
  3. 不然就shift

缺点：无法纠错。

解决方法：beam search。

Lecture 10: Statistical Machine Translation

掌握

机器翻译(Machine Translation, MT)的概念

机器翻译 (MT) 是将句子从一种语言（源语言）翻译成另一种语言（目标语言）的句子的任务。

统计机器翻译(Statistical Machine Translation, SMT)的原理

核心：从数据中学习概率模型。

image-20220109150348007

词对齐(word alignment)的概念和计算方法

概念：

源语言到目标语言的映射，是一对多的关系。

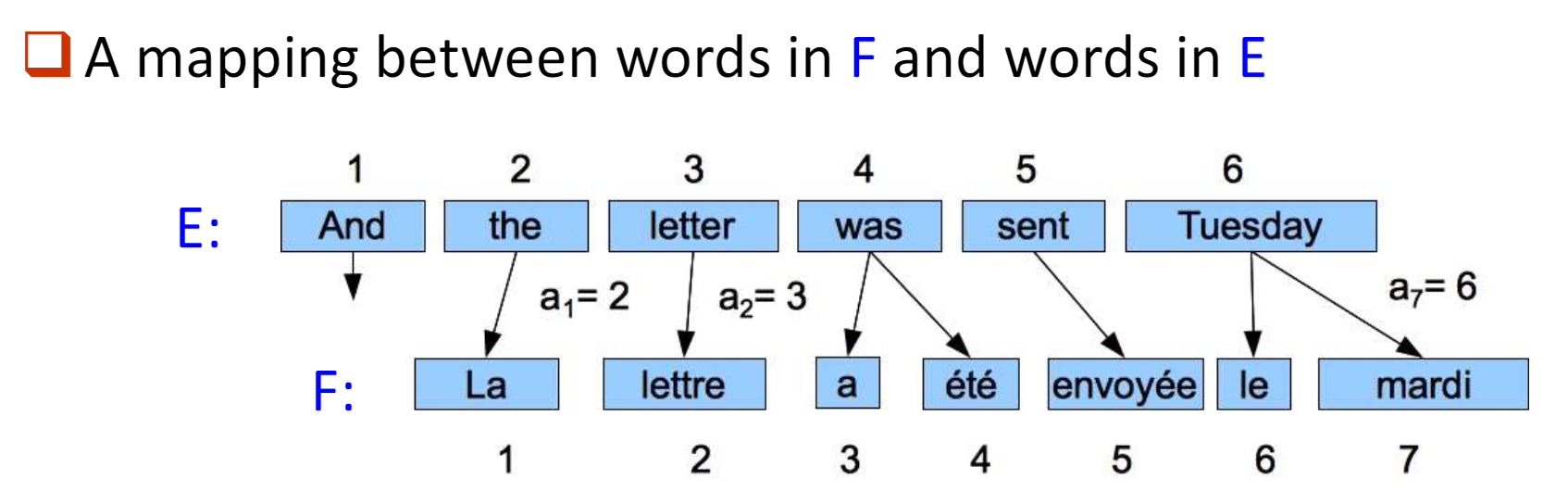
image-20220109150803968

计算方法：

\[P(F \mid E)=\sum_{A} P(F, A \mid E)\]

机器翻译评价指标(BLEU)的原理和方法

原理：

  • 翻译结果在目标语言中，更加清晰、可读和自然；
  • 翻译结果更加准确；
  • 翻译结果能够包含源语言中更多的表达信息；

如果神经机器翻译的结果和专业的人工翻译的结果越接近，那么翻译的效果就越好。“接近”的程度是通过计算翻译结果中词语和短语对人工翻译结果的命中度来评价的，也就是说BLEU的核心是对翻译结果准确度的度量。

方法：

计算 n-gram正确数 与 n-gram 总数的比值

  • n-gram正确数：同时出现在翻译结果和人工翻译结果中的n-gram数量
  • n-gram总数：在翻译结果中出现的n-gram总数

注意是共享的数量，即每次出现只能算作一次

\[\text{count-in-reference}_{clip}=\text{min}(count,max\_ref\_count)\]

表达式：

\[\text { precision }_{n}=\frac{\sum_{C \in \text { corpus } \mathrm{n}-\text { gram } \in C} \text { count-in-reference }_{\text {clip }}(\mathrm{n}-\text { gram })}{\sum_{C \in \text { corpus } \mathrm{n}-\text { gram } \in C} \text { count }(\mathrm{n}-\text { gram })}\]

如果产生的句子比较段，那么其BLEU值就会比较高。同样的，我们引入一个惩罚因子，这个惩罚因子使得译文在保证上述条件的情况下， 需要和人工翻译结果的长度匹配。具体计算如下：

\[\text { brevity-penalty }=\min \left(1, \frac{\text { output-length }}{\text { reference-length }}\right)\]

$\text { output-length }$是机器翻译结果的长度，$\text { reference-length }$是人工翻译结果的长度。我们最终计算的BLEU结果需要乘上该惩罚因子。最终计算公式为：

\[\mathrm{BLEU}-n=\min \left(1, \frac{\text { output-length }}{\text { reference-length }}\right) \prod_{i=1}^{n} \text { precision }_{i}\]

了解

IBM Model 1

生成模型：将翻译过程分解为更小的步骤。

IBM 1 只使用词法翻译。

生成过程：

image-20220109151306095

image-20220109151323737

image-20220109151338868

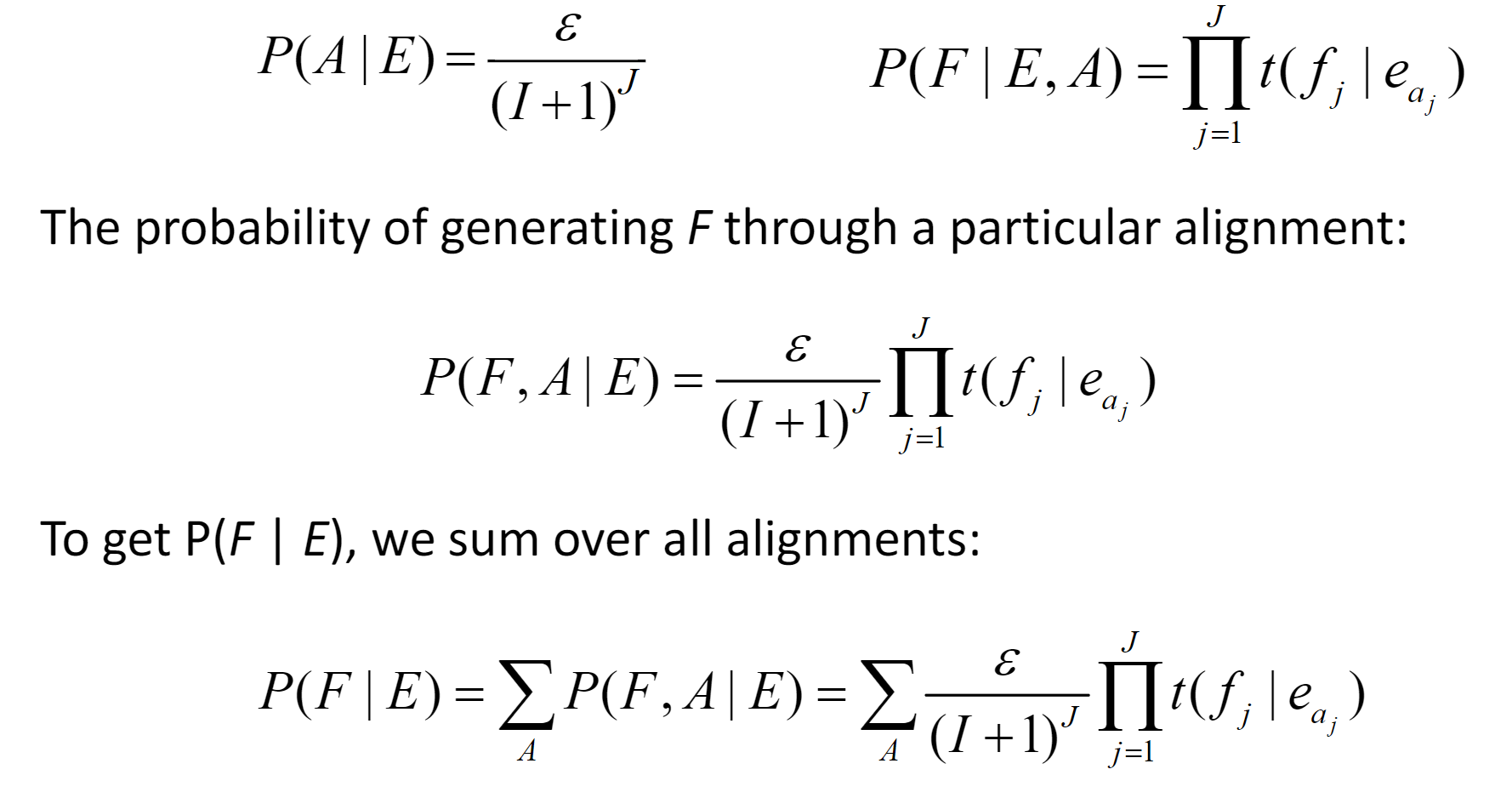
image-20220109151349477

Lecture 11: Neural Machine Translation

掌握

循环神经网络(Recurrent Neural Networks, RNN)的概念、原理、优缺点

概念：

用于处理序列数据的神经网络。

原理：

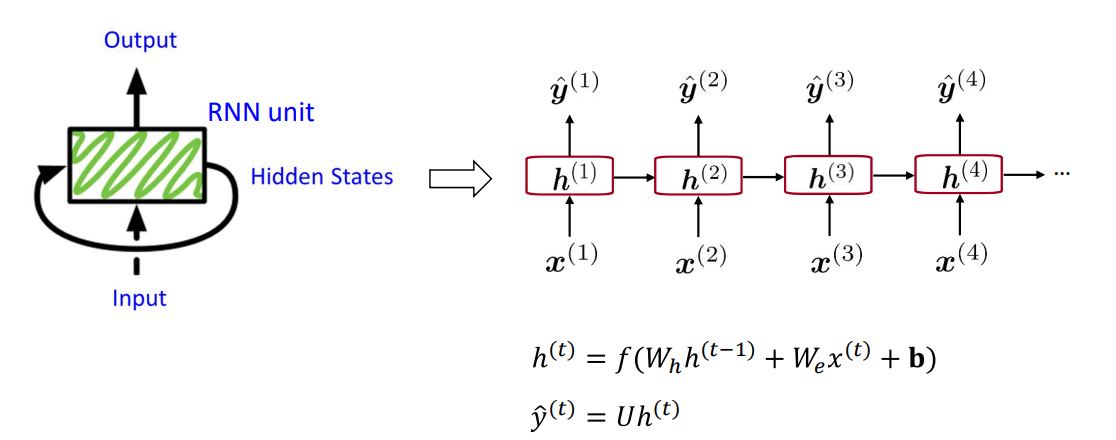
image-20220110205916334

所有的RNN单元共享相同的参数。

优点：

  • 可以输入任意长度的序列
  • 可以访问以前任何时间的信息
  • 对于长输入，模型大小不变
  • 共享权重

缺点：

  • 循环计算过程很慢
  • 事实上，当序列比较长的时候，很难获取序列相隔较远部分的信息

如何训练循环神经网络(Recurrent Neural Networks, RNN)

  1. 得到一个输入序列$x^{(1)},…,x^{(T)}$
  2. 将每个序列逐个输入RNN，并计算每个time step的输出概率
  3. 使用交叉熵计算每个time step的损失
    • 基于预测结果 $\hat{\boldsymbol{y}}^{(t)}$ 和真实的词语表示 $y^{(t)}$
\[J^{(t)}(\theta)=C E\left(\boldsymbol{y}^{(t)}, \hat{\boldsymbol{y}}^{(t)}\right)=-\sum_{w \in V} \boldsymbol{y}_{w}^{(t)} \log \hat{\boldsymbol{y}}_{w}^{(t)}\]
  1. 计算每一步的平均损失
\[J(\theta)=\frac{1}{T}\sum_{t=1}^{T}J^{(t)}(\theta)\]

神经机器翻译(Neural Machine Translation, NMT)的原理

采用一个端到端的神经网络去实现机器翻译。

这种神经网络架构称为序列到序列模型，包括了两个RNN。

序列到序列模型是一个条件概率模型，$x$是源语言，$y$是预测的下一个单词，计算$P(y x)$：
\[P(y \mid x)=P\left(y_{1} \mid x\right) P\left(y_{2} \mid y_{1}, x\right) P\left(y_{3} \mid y_{1}, y_{2}, x\right) \ldots P\left(y_{T} \mid y_{1}, \ldots, y_{T-1}, x\right)\]

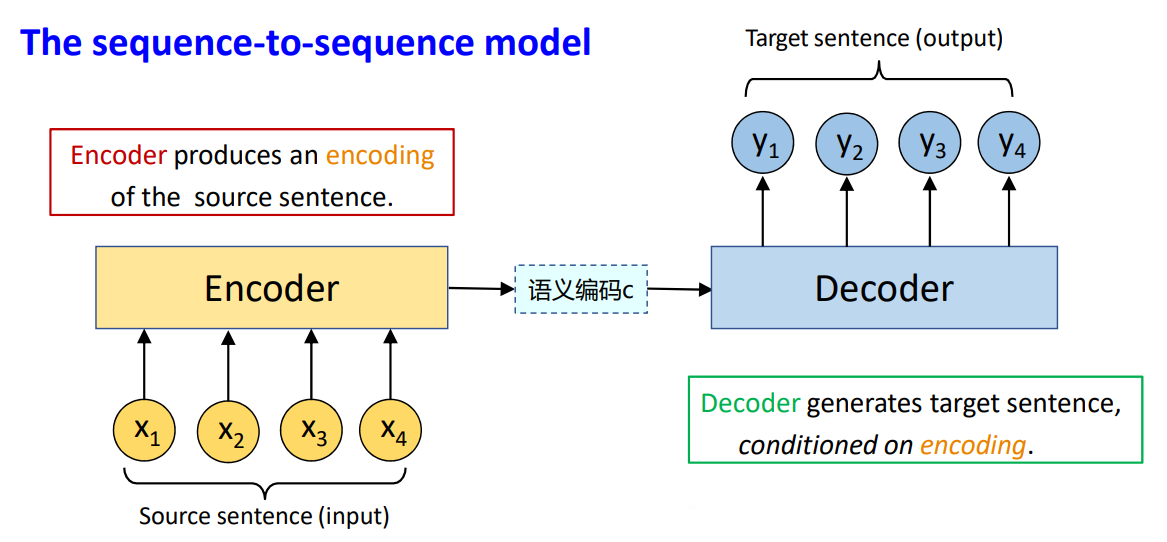
image-20220110211419182

和统计机器翻译相比，神经机器翻译的优缺点

​ 与传统的基于统计的机器翻译相比，神经机器翻译有很多优点：

  • 更好的性能：翻译结果更加清晰、可读、自然，更好地利用上下文的信息；
  • 只有单个神经网络，用于优化端到端模型；没有需要单独优化的子组件；
  • 需要更少的人力资源：无特征工作，对所有语言使用相同的方法。

​ 当然，与传统的基于统计的机器翻译相比，神经机器翻译也有一些缺点：

  • 神经机器翻译缺乏可解释性，即很难去进行调试；
  • 神经机器翻译很难进行控制：无法提供一些简单的特例和一些翻译的指引，也存在一些安全问题。

神经机器翻译的训练方法

准备一个平行语料库。

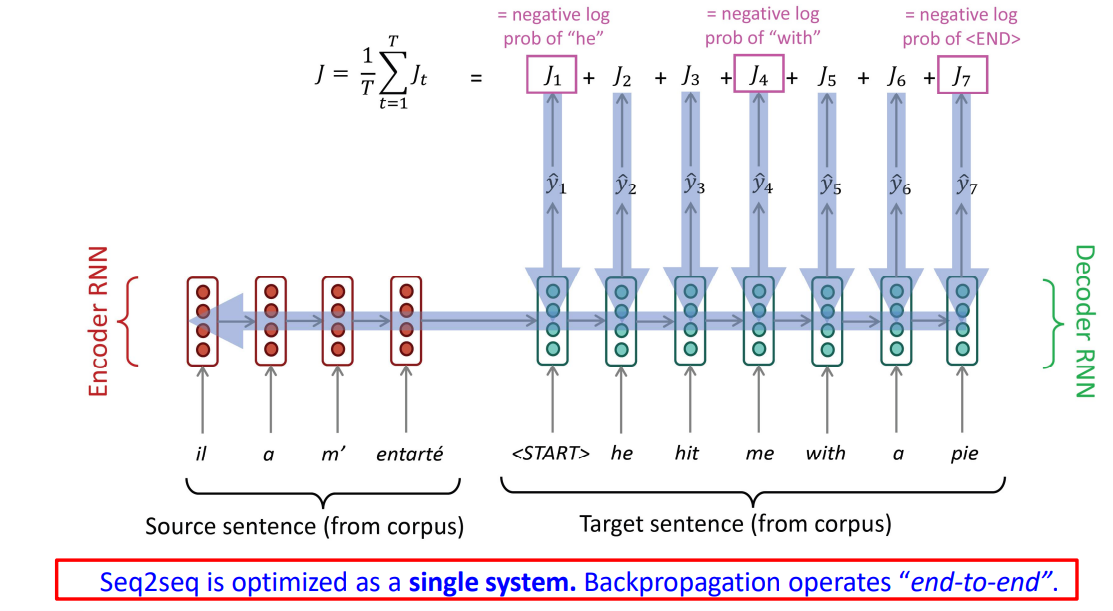
image-20220110211844656

Free-running和teacher-forcing方法的原理和不同

​ free-running模式即为，在解码器中

  • 训练过程中：当前状态的输入为上一个状态预测的结果
  • 测试过程中：当前状态的输入为上一个状态预测的结果

​ free-running模式就会产生的两个问题：模型的收敛速度会很慢，使得模型不稳定。

​ teacher-forcing模式即为，在解码器中

  • 训练过程中：当前状态的输入为上一个状态在训练集中正确的结果
  • 测试过程中：当前状态的输入为上一个状态预测的结果

​ teacher-forcing模式解决了free-running模式出现的问题，不仅模型收敛得更快，而且模型更加稳定。但是这又导致了新的问题，由于训练过程中，总是通过正确的结果进行训练，模型不具备纠正错误的能力，也就是说，模型对这种错误不具备鲁棒性。

神经机器翻译的解码方法：贪婪(greedy)和束搜索(beam search)

解码器解码出来一个词典大小的向量，每个元素表示翻译成该词语的概率。

贪婪

贪心地选取概率最大的单词。

image-20211230145450951

​ 当我们翻译出“a”的时候，实际上已经出现了翻译错误了，而我们是无法进行撤销操作的，这样就会导致错误的结果。

束搜索

核心思想：在解码器的每一步上，保留k个最可能的翻译结果。

目标是最大化分数：

\[\operatorname{score}\left(y_{1}, \ldots, y_{t}\right)=\log P_{\mathrm{LM}}\left(y_{1}, \ldots, y_{t} \mid x\right)=\sum_{i=1}^{t} \log P_{\mathrm{LM}}\left(y_{i} \mid y_{1}, \ldots, y_{i-1}, x\right)\]

为了避免长度更短的翻译结果更占优，修正模型：

\[\frac{1}{t} \sum_{i=1}^{t} \log P_{\mathrm{LM}}\left(y_{i} \mid y_{1}, \ldots, y_{i-1}, x\right)\]

结束条件

在贪心的策略中，编码出<end>即为序列编码结束。

而在beam search的过程中，在当前时间步中，最优的$k$个序列中，也可能已经出现了结束标记，这个时候，我们需要将这些序列保存为最终的待选答案之一，并将$k$的大小减小1，续进行计算，直到$k$的大小为0。

注意力机制(attention)

​ 普通的RNN模型存在两个问题：

  1. 把整个输入序列$\mathbf{X}$压缩到一个固定长度的语义编码$c$，忽略了输入序列的长度，当输入句子长度很长，特别是比训练集中最初的句子长度还长时，模型的性能急剧下降。
  2. 把输入序列$\mathbf{X}$编码成一个固定的长度，对于句子中每个词都赋予相同的权重，这样做是不合理的，比如，在机器翻译里，输入的句子与输出句子之间，往往是输入一个或几个词对应于输出的一个或几个词。因此，对输入的每个词赋予相同权重，这样做没有区分度，往往使模型性能下降。

​ 解决这个问题最好的方法，就是引进attention。使用了attention后，seq2seq模型翻译的时候会再看一遍整个句子的状态，这样就解决了遗忘的问题。attention还会告诉decoder应该关注encoder的哪些状态，这样就能解决第二个缺点。

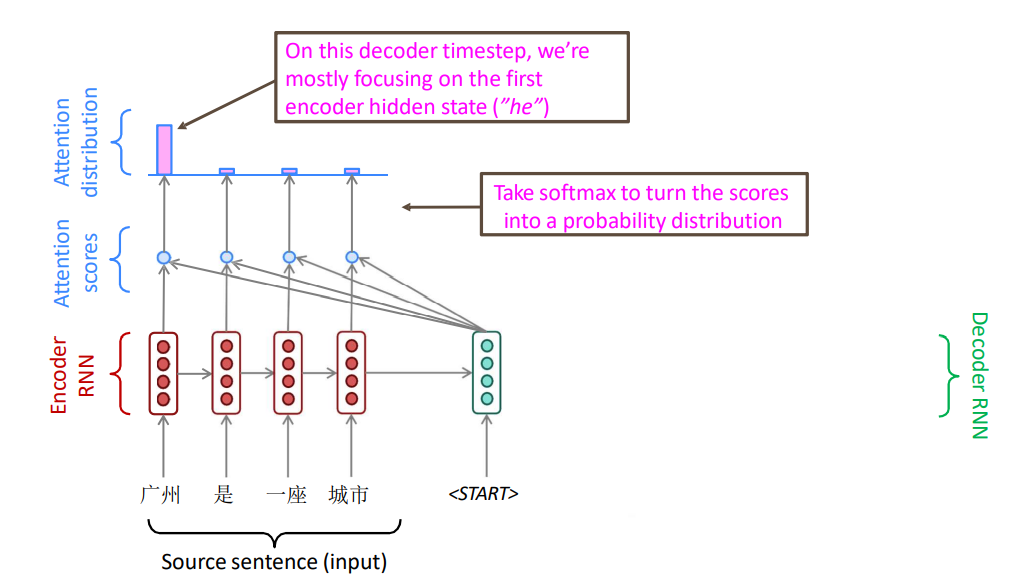
image-20220110212529953

我们将解码器当前的输入$x^{(i)}$与编码器每一步的编码结果$\mathbf{Y}$做点积，得到当前输入对编码器每个状态编码信息的注意力权重（当然计算方法有很多，这里介绍的是点积模型）。因此，对于当前输入，我们得到该输入对于源句子每个词语的注意力权重$\hat{y}^{(i)}$，最后对所有$\mathbf{Y}$做一次softmax操作，即将所有的$\hat{y}^{(i)}$进行归一化，使得$\sum\hat{y}^{(i)}=1$。

\[\operatorname{softmax}(z)=\left[\frac{\exp \left(z_{1}\right)}{\sum_{i=1}^{k} \exp \left(z_{i}\right)}, \frac{\exp \left(z_{2}\right)}{\sum_{i=1}^{k} \exp \left(z_{i}\right)}, \ldots, \frac{\exp \left(z_{k}\right)}{\sum_{i=1}^{k} \exp \left(z_{i}\right)}\right]\]

​ 归一化后，我们就得到该输入的注意力分布情况。注意力分布可以解释为在上下文查询时，第 i 个信息受关注的程度。那么，我们最后的编码输入即为，所有隐向量与注意力分布的加权平均。公式表达如下：

​ 编码器的隐状态 $h_{1}, \ldots, h_{N} \in \mathbb{R}^{h}$。

​ 在时间 $t$，解码器隐状态 $s_{t} \in \mathbb{R}^{h}$ 。

​ 我们得到每一步的注意力分数为 $e^{t}$ ：

\[\boldsymbol{e}^{t}=\left[\boldsymbol{s}_{t}^{T} \boldsymbol{h}_{1}, \ldots, \boldsymbol{s}_{t}^{T} \boldsymbol{h}_{N}\right] \in \mathbb{R}^{N}\]

​ 对注意力分数进行softmax操作得到注意力分布每一步的 $\alpha^{t}$，其中$\sum a^t=1$

\[\alpha^{t}=\operatorname{softmax}\left(\boldsymbol{e}^{t}\right) \in \mathbb{R}^{N}\]

​ 我们使用 $\alpha^{t}$ 对编码器隐状态做加权平均，得到 $\boldsymbol{a}_{t}$：

\[\boldsymbol{a}_{t}=\sum_{i=1}^{N} \alpha_{i}^{t} \boldsymbol{h}_{i} \in \mathbb{R}^{h}\]

​ 最后将 $\boldsymbol{a}{t}$ 跟解码器隐状态进行合并， $\left[\boldsymbol{a}{t} ; \boldsymbol{s}_{t}\right] \in \mathbb{R}^{2 h}$ ，后面的操作跟普通RNN模型相同。

了解

神经机器翻译的实现

​ 无

CATALOG
    FEATURED TAGS
    神经网络 机器学习 机器人 webot 通信原理 并行计算 信息安全 自然语言处理 数据库 数字图像处理 软件工程 编译原理 强化学习 数字电路 proteus 计算机组成原理 VIVADO JAVA 论文阅读 组合优化 NIPS