1 实验目的
回顾一学期所学的知识,尤其是逻辑表达式的化简、组合逻辑设计以及移位寄存器芯片的使用。
2 实验要求
(1)BCD码与“余1码”的相互转换。
(2)输入不合法码要报错。
(3)四位代码由拨号开官输入,BCD码送7段数码管显示,余1码送发光二极管显示。
3 实验思路
(1)转换部分逻辑表达式的设计
不妨假设$A$、$B$、$C$、$D$为四位BCD码,$1$、$2$、$3$、$4$为四位余1码。
它们间的转换关系用真值表的形式表现如下:
| A | B | C | D | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
根据真值表的对应关系,可以画出卡诺图。有一点技巧,在BCD码转换余1码的卡诺图中,由于输入$10$到$15$是不合法的,因此可以将它们作为冗余项加入卡诺图中;同样的,在余1码转换BCD码的时候,输入$11$到$15$以及$0$,也是不合法的,同样可以作为冗余项,以达到化简的目的。在以下卡诺图中,用$1$表示原本的$SOP$表达式,$x$作为添加的冗余项。
对$1$:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | ||||
| 01 | 1 | |||
| 11 | x | x | x | |
| 10 | 1 | 1 |
对$2$:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | |||
| 01 | 1 | 1 | 1 | |
| 11 | x | x | x | |
| 10 | x |
对$3$:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 1 | ||
| 01 | 1 | 1 | ||
| 11 | x | x | ||
| 10 | 1 | x |
对$4$:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 1 | ||
| 01 | 1 | 1 | ||
| 11 | x | x | ||
| 10 | 1 | x |
对$A$:
| 01\23 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | ||||
| 01 | ||||
| 11 | x | x | x | |
| 10 | 1 | x | 1 |
对$B$:
| 01\23 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | x | |||
| 01 | 1 | 1 | 1 | |
| 11 | x | x | x | |
| 10 | 1 |
对$C$:
| 01\23 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | |||
| 01 | 1 | 1 | ||
| 11 | ||||
| 10 | 1 |
对$D$:
| 01\23 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | 1 | ||
| 01 | 1 | 1 | ||
| 11 | x | x | ||
| 10 | 1 | x |
因此得出结论:
$1=A\bar{C}+BCD$
$2=B(\bar{C}+\bar{D})+\bar{B}CD$
$3=\bar{A}(C\oplus D)+AD$
$4=\bar{D}$
$A=13+14$
$B=23+24+\bar{2}\bar{3}\bar{4}$
$C=\bar{1}34+\bar{3}\bar{4}(1\oplus 2)$
$D=\bar{4}$
(2)输入检测
(2).1 BCD码检测
对于BCD码,$10$到$15$是不合法的输入,画出卡诺图如下:
| AB\CD | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | ||||
| 01 | ||||
| 11 | 1 | 1 | 1 | 1 |
| 10 | 1 | 1 |
即$X=AC+AB$
(2).2 余1码检测
对于余1码,$11$到$15$以及$0$是不合法的输入,画出卡诺图如下:
| 01\23 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 00 | 1 | |||
| 01 | ||||
| 11 | 1 | 1 | 1 | 1 |
| 10 | 1 |
即$X=12+134+\bar{1}\bar{2}\bar{3}\bar{4}$
(3)串行输入
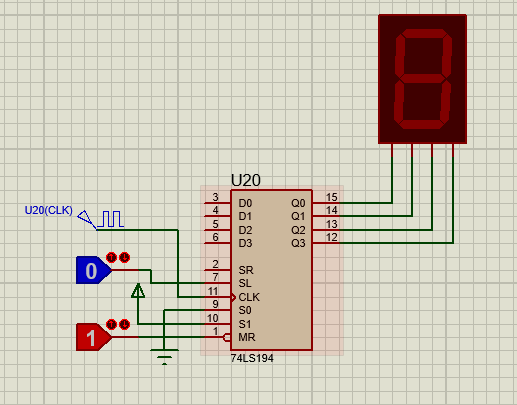
使用74LS194芯片,即移位寄存器作为串行输入。在SL端加入串行输入,S0和S1置为0和1表示右移。使用方法为在每个时钟上升沿到来前更改SL的输入。
4 实验步骤
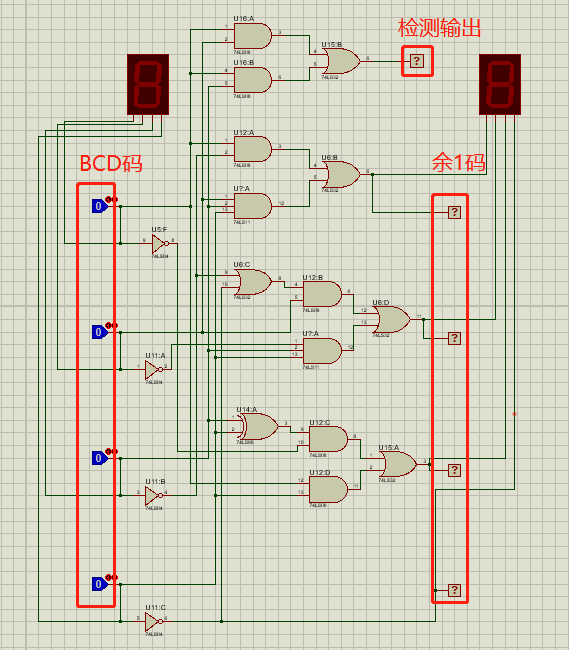
(1)BCD码转余1码电路
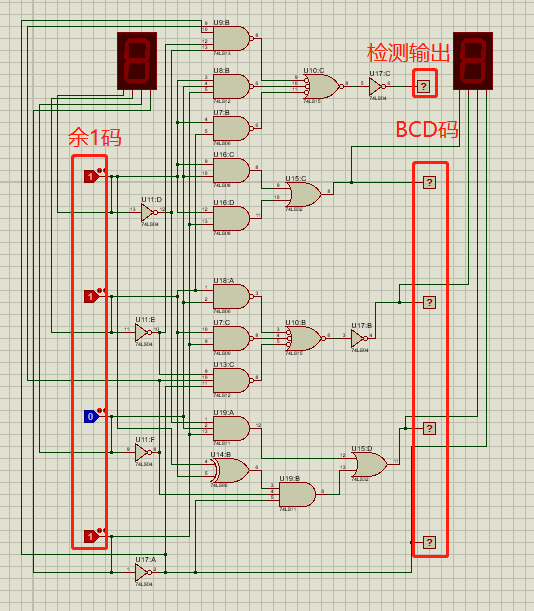
(2)余1码转BCD码
(3)串行输入
5 实验结果
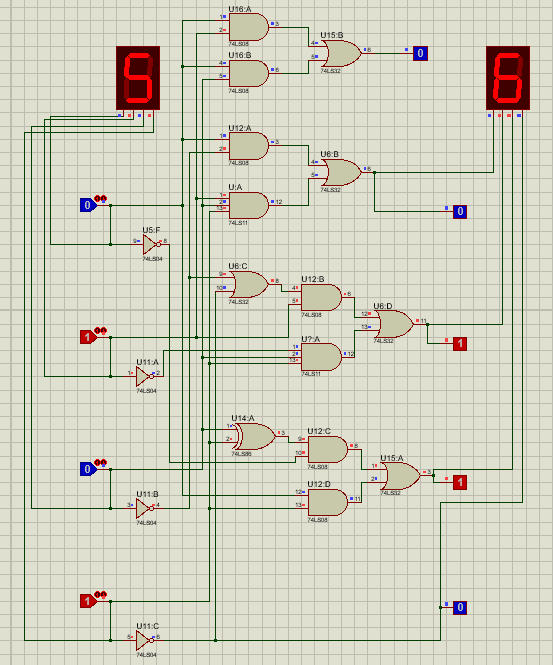
5.1 BCD码转换测试
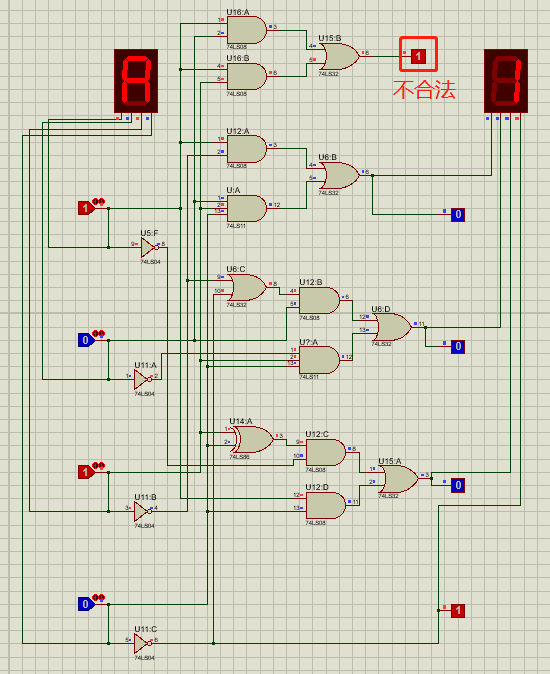
输入5,输出6,显示输入合法。
输入12,显示不合法。
5.2 余1码转换
输入7,输出6,显示合法。
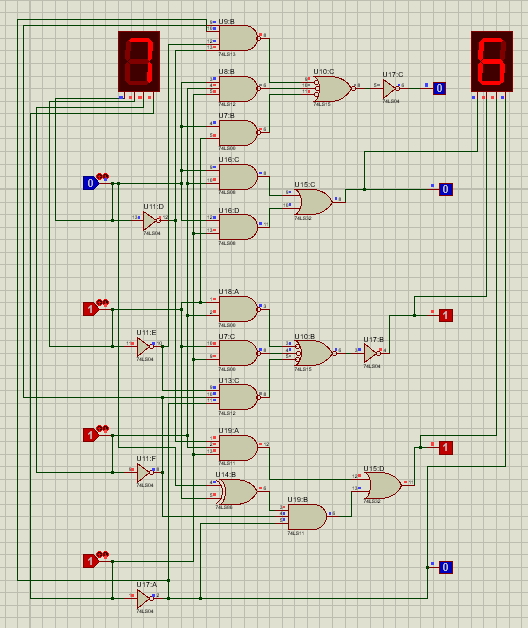
输入0,显示不合法。
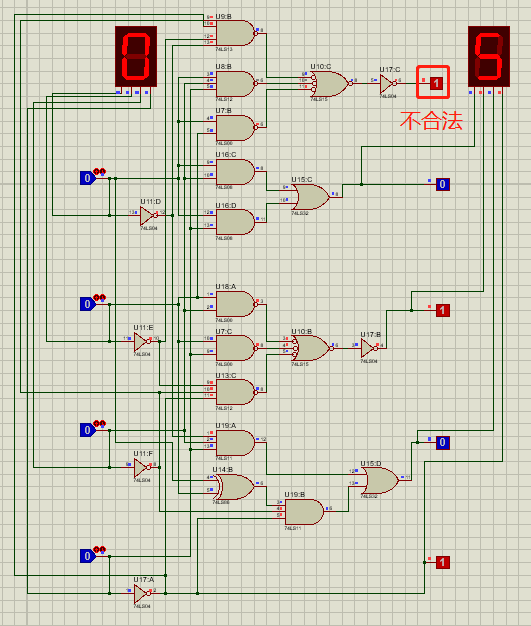
注:由于并行输入仅需要将输入上述的输入部分更改成并行输入模块(上一部分已实现),其他电路均一致,故没有展示。
6 实验感想
其实在实验过程中,我还实现了另外一个电路。
BCD码转余1码其实就是实现加1的过程,反之也是差不多的。因此,对整个电路只需要实现四个半加器即可完成电路转换。
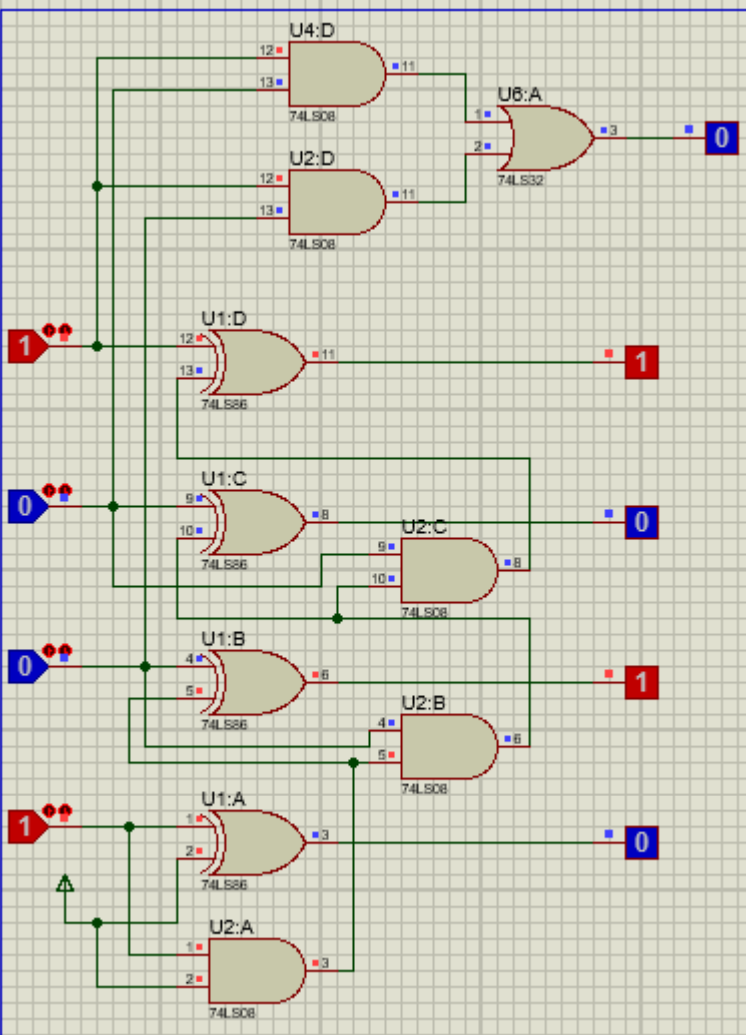
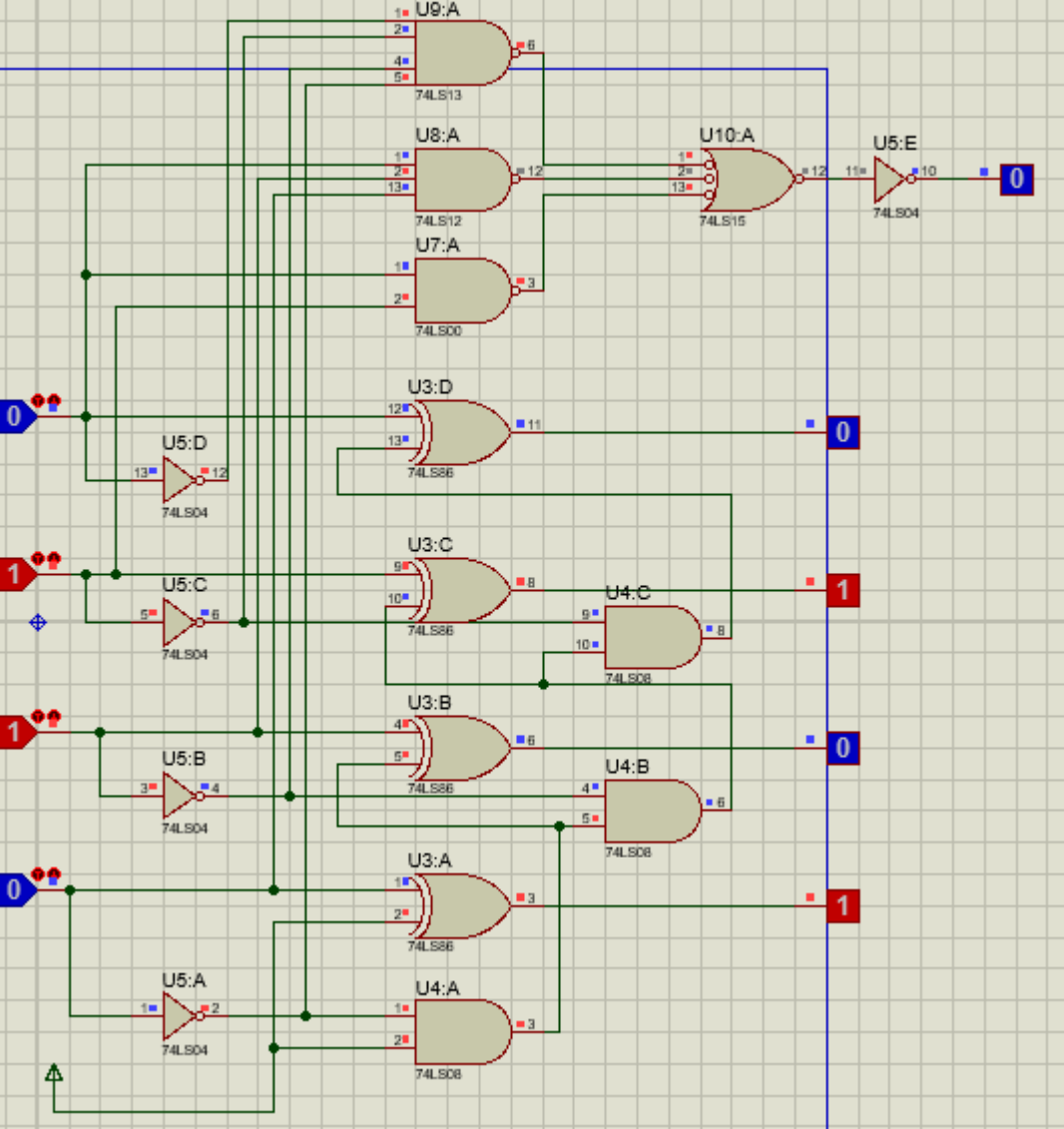
但本着严谨的学习态度,以及领悟老师想考核的内容,还是将其更改为更加复杂和繁琐的逻辑门和组合电路设计。
通过本学期数字电路实验课的学习,我学习到了很多知识,我掌握了proteus以及vivado相关软件的使用,对很多元器件的引脚和特性都已经非常熟悉,我还学会了如何把子电路封装成一个元器件,我学会了如何把8*8点阵做成16*16点阵,我学会了做多谐振荡器、节拍发射器等等。刚接触这门课的实验的时候,总是怕自己做不好实验,怕自己做的实验得不到想象中的效果,在不断的学习过程中,随着助教和老师的讲解,我学会的越来越多,做的实验也越来越得心应手,自己出错搞不懂的问题也会在群里询问,和亲切友好的大佬同学和助教老师进行讨论和交流,同一种实验每次都能学习到很多种不同的思想,自己学会的也越来越多。每次做实验都是对理论知识的一种复习和掌握,随着实验做得越来越得心应手和擅长,我对于理论知识的理解也是越来越深刻,不管是化简卡诺图还是列表达式,我的能力都大大加强,虽然我还有着粗心大意的毛病,做实验经常连错线,化简表达式也时不时简化错,但是每一次的错误都让我下一次更加的仔细认真。把自己的实验电路一点点完善,一点点做完,就像是看着自己的孩子渐渐长大一样,有趣又欣慰,看着自己设计的电路实现了它应有的功能,哪怕不是最好最简便的设计,但是过程中的满足感不言而喻。