实验环境
操作系统: Windows 11
Python:Python 3.8.6
matlab:MATLAB2021b
处理器:AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz
实验1 一范数规范化最小二乘
1.1 问题描述
考虑一个 20 节点的分布式系统。节点 $i$ 有线性测量 $b_i=A_ix+e_i$,其中 $b_i$ 为 10 维的测量值,$A_i$ 为 10ⅹ300 维的测量矩阵,$x$ 为 300 维的未知稀疏向量且稀疏度为 5,$e_i$ 为 10 维的测量噪声。从所有 $b_i$ 与 $A_i$ 中恢复 $x$ 的一范数规范化最小二乘模型如下:
\[\min \frac{1}{2}\|A_1x-b_1\|_2^2 +…+\frac{1}{2}\|A_{20}x-b_{20}\|_2^2 +p\|x\|_1\]其中 $p$ 为非负的正则化参数。请设计下述分布式算法求解该问题:
1、邻近点梯度法;
2、交替方向乘子法;
3、次梯度法;
在实验中,设 $x$ 的真值中的非零元素服从均值为 0 方差为 1 的高斯分布,$A_i$ 中的元素服从均值为 0 方差为 1 的高斯分布,$e_i$ 中的元素服从均值为 0 方差为 0.2 的高斯分布。对于每种算法,请给出每步计算结果与真值的距离以及每步计算结果与最优解的距离。此外,请讨论正则化参数 $p$ 对计算结果的影响。
1.2 算法设计
1.2.1 邻近点梯度法
对于该问题,目标函数
\[f_0(x)=\frac{1}{2}\|A_1x-b_1\|_2^2 +…+\frac{1}{2}\|A_{20}x-b_{20}\|_2^2 +p\|x\|_1\]$f_0$ 可以分为两个部分
\[f_0(x) = s(x)+r(x)\\\]其中
\[\begin{aligned} s(x) &= \frac{1}{2}\|A_1x-b_1\|_2^2 +…+\frac{1}{2}\|A_{20}x-b_{20}\|_2^2\\ r(x) &= p\|x\|_1 \end{aligned}\]$s(x)$ 为 $f_0(x)$ 中可微且易求导的部分,而 $r(x)$ 为 $f_0(x)$ 中不可微但易求邻近点投影的部分。
邻近点梯度法可以写成
\[\begin{aligned} x^{k+\frac{1}{2}} &= x_k + \alpha\triangledown s(x^k)\\ x^{k+1} &= \arg\min r(x) + \frac{1}{2\alpha}\|x-x^{k+\frac{1}{2}}\|_2^2 \end{aligned}\]其中,$\alpha$ 为步长。光滑部分的梯度为
\[\triangledown s(x) = \sum_{i=1}^{20} A_i^T(A_ix^k+b_i)\]带入具体的目标函数,有
\[\begin{aligned} x^{k+\frac{1}{2}} &= x_k + \alpha\sum_{i=1}^{20} A_i^T(A_ix^k+b_i)\\ x^{k+1} &= \arg\min p\|x\|_1 + \frac{1}{2\alpha}\|x-x^{k+\frac{1}{2}}\|_2^2 \end{aligned}\]考虑如何求 $\arg\min p|x|_1 + \frac{1}{2\alpha}|x-x^{k+\frac{1}{2}}|_2^2$,由于 $p|x|_1$ 不可微,那么对该表达式求次梯度,有
\[\begin{aligned} x^{k+1} &= \arg\min p\|x\|_1 + \frac{1}{2\alpha}\|x-x^{k+\frac{1}{2}}\|_2^2 \\ &= \arg\min p\sum_{i=1}^{20}|x_i| + \frac{1}{2\alpha}\sum_{i=1}^{20}(x_i-x_i^{k+\frac{1}{2}})^2 \\ &= \forall i\arg\min p|x_i| + \frac{1}{2\alpha}(x_i-x_i^{k+\frac{1}{2}})^2 \end{aligned}\]此时 $x$ 的每一维都是独立的,对于第 $i$ 维,最优性条件为:$∃$次梯度=0。分类讨论:
-
当$x_i>0$,最优性条件为
\[p+\frac{1}{\alpha}(x_i-x_i^{k+\frac{1}{2}})=0\]即
\[x_i=x_i^k-p\alpha\]那么当 $x_i^k - p\alpha > 0$时,有
\[x_i = x_i^k - p\alpha\] -
当$x_i<0$,最优性条件为
\[-p+\frac{1}{\alpha}(x_i-x_i^{k+\frac{1}{2}})=0\]即
\[x_i=x_i^k+p\alpha\]那么当 $x_i^k + p\alpha > 0$时,有
\[x_i = x_i^k + p\alpha\] -
当$x_i=0$,最优性条件为
\[0\in [-p+\frac{1}{\alpha}(x_i-x_i^{k+\frac{1}{2}}), p+\frac{1}{\alpha}(x_i-x_i^{k+\frac{1}{2}})]\]由于$x_i=0$,那么当 $x_i^k \in [-p\alpha,p\alpha]$时,有
\[x_i = 0\]
1.2.2 交替方向乘子法
交替方向乘子法用于有约束优化问题。对于如下问题
\[\min f_1(x)+f_2(y)\\ s.t. Ax+By=0\]其增广拉格朗日函数为
\[L_c(x,y,\lambda)=f_1(x)+f_2(x)+\lambda(Ax+By)+\frac{c}{2}\|Ax+By\|^2\]其中,$c$ 是一个大于 0 的常数。
交替方向乘子法表示为
\[\begin{aligned} (x^{k+1},y^{k+1}) &= \arg\max_{x,y} L_c(x,y,\lambda^k) \\ \lambda^{k+1} &= \lambda^k+c(Ax^{k+1}+By^{k+1}) \end{aligned}\]将更新函数解耦合后,有
\[\begin{aligned} x^{k+1} &= \arg\max_{x} L_c(x,y^k,\lambda^k) \\ y^{k+1} &= \arg\max_{y} L_c(x^{k+1},y,\lambda^k) \\ \lambda^{k+1} &= \lambda^k+c(Ax^{k+1}+By^{k+1}) \end{aligned}\]原问题是无约束优化问题,需要转换为有约束优化问题,令
\[\begin{aligned} &f_i(x)=\frac{1}{2}\|A_ix-b_i\|_2^2\\ &g(x)=p\|x\|_1 \end{aligned}\]那么原问题可转化为
\[\begin{aligned} & \min\sum_{i=1}^{20}f_i(x_i)+g(z) \\ & s.t. \forall i\ x_i=z \end{aligned}\]其增广拉格朗日函数为
\[L_c(\lbrace x_i\rbrace,z,\lbrace\lambda_i\rbrace)=\sum_{i-1}^{20}f_i(x_i)+g(z)+\sum_{i=1}^{20} \lambda_i(x_i-z)+\frac{c}{2}\sum_{i=1}^{20}\|x_i-z\|^2\]由此可以看出该问题不适合使用增广拉格朗日法。采用交替方向乘子法得到更新如下:
\[\begin{aligned} x_i^{k+1} &= \arg\min_{x_i} L_c(x_i,z^k,\lambda_i^k) \\ z^{k+1} &= \arg\min_{z} L_c(\lbrace x_i^{k+1}\rbrace,z,\lbrace\lambda_i^k\rbrace) \\ \lambda_i^{k+1} &= \lambda_i^k+c(x_i^{k+1}-z^{k+1})\ \forall i \end{aligned}\]带入增广拉格朗日函数,并去掉无关的项,有
\[\begin{aligned} x_i^{k+1} &= \arg\min_{x_i} f_i(x_i)+\lambda_i^kx_i+\frac{c}{2}\|x_i-z^k\|^2 \\ z^{k+1} &= \arg\min_{z} g(z)-\sum_{i=1}^{20}\lambda_i^kz+\frac{c}{2}\sum_{i=1}^{20}\|x_i^{k+1}-z\|^2 \\ \lambda_i^{k+1} &= \lambda_i^k+c(x_i^{k+1}-z^{k+1})\ \forall i \end{aligned}\]-
对于 $x_i^{k+1}$,最优性条件为
\[\triangledown_{x_i}(f_i(x_i)+\lambda_i^kx_i+\frac{c}{2}\|x_i-z^k\|^2)=0\]即
\[A_i^T(A_ix_i-b_i)+\lambda_i^k+c(x_i-z^k)=0\]可得
\[x_i^{k+1}=(A_i^TA_i+cI)^{-1}(cz^k+A_i^Tb_i-\lambda_i^k)\] -
对于 $z^{k+1}$,由于 $g(z)$ 不可微,因此最优性条件为:$∃$次梯度=0。$z$ 中的每一维独立,对于每一维单独考虑。考虑第 $j$ 维:
(1)当 $z_j>0$,最优性条件为
\[p-\sum_{i=1}^{20}\lambda_{i,j}^k+c\sum_{i=1}^{20}(z_j-x_{i,j}^{k+1})=0\] 由于 $c$ 是大于 0 的常数,即当
\[\sum_{i=1}^{20}\lambda_{i,j}^k-p+c\sum_{i=1}^{20}x_{i,j}^{k+1}>0\] 有
\[z_j^{k+1}=\frac{\sum_{i=1}^{20}\lambda_{i,j}^k-p+c\sum_{i=1}^{20}x_{i,j}^{k+1}}{20c}\](2)当 $z_j<0$,最优性条件为
\[-p-\sum_{i=1}^{20}\lambda_{i,j}^k+c\sum_{i=1}^{20}(z_j-x_{i,j}^{k+1})=0\] 由于 $c$ 是大于 0 的常数,即当
\[\sum_{i=1}^{20}\lambda_{i,j}^k+p+c\sum_{i=1}^{20}x_{i,j}^{k+1}>0\] 有
\[z_j^{k+1}=\frac{\sum_{i=1}^{20}\lambda_{i,j}^k+p+c\sum_{i=1}^{20}x_{i,j}^{k+1}}{20c}\](3)其他情况下,$z_j=0$。
1.2.3 次梯度法
对目标函数
\[f_0(x)=\frac{1}{2}\|A_1x-b_1\|_2^2 +…+\frac{1}{2}\|A_{20}x-b_{20}\|_2^2 +p\|x\|_1\]由于目标函数不可微,令 $g_0(x)$ 为 $f_0(x)$ 的次梯度。
次梯度法的更新形式为
\[x^{k+1}=x^{k}-\alpha^{k}g_0(x^k)\]-
目标函数中,最小二乘部分 $\frac{1}{2}|A_1x-b_1|2^2 +…+\frac{1}{2}|A{20}x-b_{20}|_2^2$ 可微,其次梯度等于梯度,可写成
\[\sum_{i=1}^{20} A_i^T(A_ix^k+b_i\] -
一范数部分中,令$r(x)=p|x|_1$ ,$r(x)$ 的次梯度为
\[\partial r(x_i)=\left\lbrace\begin{aligned} -p,x_i<0\\ +p,x_i>0\\ [-p,p],x_i=0 \end{aligned} \right.\]
两者相加即为 $g_0(x)$。
对于步长 $\alpha^{k}$,一般使用递减步长。可证明,当
\[\alpha^{k}=\frac{1}{\sqrt{k+1}}\]其中 $k$ 为计算的轮数,收敛速度可达 $O(\frac{\log k}{\sqrt{k}})$ 的量级。
1.3 数值实验
该部分包含具体的代码分析以及实验结果。
1.3.1 生成数据
生成向量和矩阵(generator.m)。
%% 生成 A, x, b 和 e
n = 20; % 节点个数
% 生成 x 向量
x = zeros(300, 1); % 生成一个全零向量
index = randi(300, 1, 5); % 生成5(稀疏度)个填充位置
for i = 1 : 5
x(index(i)) = normrnd(0,1); % 将5个位置用(0, 1)的高斯分布填充
end
% 生成 A, e并计算b
A = zeros([n, 10, 300]); % 初始化A的大小为20x10x300
e = zeros([n, 10]); % 初始化e的大小为20x10
b = zeros([n, 10]); % 初始化b的大小为20x10
for i = 1 : n
Ai = normrnd(0, 1, [10, 300]); % 生成10x300的(0, 1)高斯分布矩阵
ei = normrnd(0, 0.2, [10, 1]); % 生成10x1的(0, 0.2)高斯分布向量
bi = Ai * x + ei; % 计算bi
A(i,:,:) = Ai;
e(i,:) = ei;
b(i,:) = bi;
end
%% 保存
save('A.mat','A')
save('b.mat','b')
save('x.mat','x')
设置常量(三个算法计算前的设置)。
%% 常量设置
n = 20; % 节点个数
epochs = 10000; % 迭代轮数
c = 0.001; % 步长
p = 0.1; % 正则化参数
xsize = 300; % x维度的大小,后面频繁用到
load('A.mat');
load('b.mat');
load('x.mat');
1.3.2 邻近点梯度法
xk = zeros([xsize, 1]); % 初始化x^(0),以全零向量作为起点
storgeXk = zeros([xsize, epochs]); % 存储每一轮迭代计算的x^(k),其中第一维为向量,第二维为迭代轮数
% 数组第一维不能超过300维, 因此迭代轮数放在第二维
for k = 1 : epochs % 迭代轮数
% 计算 x^(k+1/2) = x^k - c * sum delta S
sumDeltaS = 0; % 20个最小二乘梯度的和
for i = 1 : n % 假的20个节点的分布式计算
Ai = reshape(A(i,:,:), 10, xsize); % 获取Ai
bi = reshape(b(i,:), 10, 1); % 获取bi
deltaS = Ai' * (Ai * xk - bi); % 计算最小二乘的梯度
sumDeltaS = sumDeltaS + deltaS; % 累加和
end
xk12 = xk - alpha * sumDeltaS; % 更新x^(k+1/2)
% 计算 x^(k+1) = argmin p\|x\|1 + (1\2alpha) \|x-x^(k+1/2)\|^2
for i = 1 : xsize % 对于每一维单独考虑
% 三种情况情况的分类讨论,等于0的情况由于初始值为0,不需要额外考虑
if xk12(i) - alpha * p > 0
xk(i) = xk12(i) - alpha * p;
elseif xk12(i) + alpha * p < 0
xk(i) = xk12(i) + alpha * p;
end
end
storgeXk(:,k) = xk; % 存储该轮的计算结果
end
1.3.3 交替方向乘子法
%% 预处理,计算一些在迭代过程中反复使用的常量,这些常量计算一次即可
pre = zeros([n, xsize, xsize]); % 20个(Ai^T * Ai + c * I) ^ -1
ATb = zeros([n, xsize]); % 20个A^T * b
for i = 1 : n % 20个节点
% 计算 (A^T * A + C * I) ^ -1
Ai = reshape(A(i,:,:), 10, xsize); % 取出Ai
bi = reshape(b(i,:), 10, 1); % 取出bi
I = eye(xsize); % 单位矩阵
pre(i, :, :) = (Ai' * Ai + c * I) ^ -1;
% 计算 A^T * b
ATb(i, :) = Ai' * bi;
end
%% 迭代计算
xk = zeros([n, xsize]); % 20个xi^(k)
zk = zeros([xsize, 1]); % z^(k)
lambdak = zeros([n, xsize]); % 20个lambda^k
storgeZk = zeros([xsize, epochs]); % 存储 z^(k), z^(k)是最终的优化目标
for k = 1 : epochs
% 计算 xi^(k+1) = (Ai^T * Ai + c * I)^-1 * (c * z^k + A^T * b - lambdai^k)
for i = 1 : n
prei = reshape(pre(i, :, :), xsize, xsize); % 取出(Ai^T * Ai + c * I) ^ -1
ATbi = reshape(ATb(i, :), xsize, 1); % 取出A^T * b
lambdaik = reshape(lambdak(i,:), xsize, 1); % 取出lambdai^k
xk(i,:) = prei * (c * zk + ATbi - lambdaik);
end
% 计算 z^(k+1) = argmin g(z) - sum lambdai^k * z + (c/2) sum \|xi^(k+1) - z\|^2
sumlambdak = reshape(sum(lambdak, 1), xsize, 1); % n个lambdai^k的和
sumxk = reshape(sum(xk, 1), xsize, 1); % n个x^(k+1)的和
for j = 1 : xsize % 次梯度,每个维度单独算
% 三种情况情况的分类讨论
if sumlambdak(j) - p + c * sumxk(j) > 0 % zj > 0
zk(j) = (sumlambdak(j) - p + c * sumxk(j)) / (n * c);
elseif sumlambdak(j) + p + c * sumxk(j) < 0 % zj < 0
zk(j) = (sumlambdak(j) + p + c * sumxk(j)) / (n * c);
else % zj = 0
zk(j) = 0;
end
end
% 计算 lambdai^(k+1) = lambdai^k + c(xi^(k+1) - z^(k+1))
for i = 1 : n
lambdak(i, :) = lambdak(i, :) + c * (xk(i, :) - reshape(zk, 1, xsize));
end
% 存储第k轮的计算结果
storgeZk(:,k) = zk;
end
1.3.4 次梯度法
alphak = alpha; % 初始化alpha^(0)
xk = zeros([xsize, 1]); % 初始化x^(k)为全零向量
storgeXk = zeros([xsize, epochs]); % 存储 x^(k), 数组第一维不能超过300维
for k = 1 : epochs % 迭代轮数
% 计算 sum AT(Ax-b)
subgradient1 = zeros([xsize, 1]);
for i = 1 : n
% \|Aix - bi\|^2 的次梯度
Ai = reshape(A(i, :), 10, xsize); % 取出Ai
bi = reshape(b(i, :), 10, 1); % 取出bi
subgradient1 = subgradient1 + Ai' * (Ai * xk - bi);
end
% p\|x\| 的次梯度
xgradient = zeros([xsize, 1]);
for j = 1 : xsize % 对每一维单独考虑
if xk(j) == 0 % xj=0
xgradient(j) = rand() * 2 - 1; % [-1, 1]上的随机数
else % xj = sign(xj)
xgradient(j) = sign(xk(j));
end
end
xgradient = p * xgradient(:);
% 更新x^(k+1)
xk = xk - alphak * (subgradient1 + xgradient);
% 更新alpha^(k+1)
alphak = alpha / sqrt(k + 1);
% 存储第k轮的计算结果
storgeXk(:,k) = xk;
end
1.3.5 画图并比较
dis2opt = zeros(epochs);
dis2real = zeros(epochs);
for i = 1 : epochs
dis2opt(i) = norm(storgeXk(:,i) - storgeXk(:,epochs), 2); % 与最优解的距离
dis2real(i) = norm(storgeXk(:,i) - x, 2); % 与真值的距离
end
hold on
plot(dis2opt);
plot(dis2real);
xlabel('epoch');
ylabel('distance');
title('Adjacent Point Gradient'); % 方法的名称
legend('distence to opt', 'distence to real');
1.3.6 实验结果
一些参数的设置如下
| 参数名称 | 值 | 含义 |
|---|---|---|
| epochs | 10000 | 迭代轮数 |
| c \ alpha | 0.001 | 步长 |
| p | 0.1 | 正则化参数 |
以上为标准测试样例。具体的参数设置比较将在1.4中阐述。
邻近点梯度法
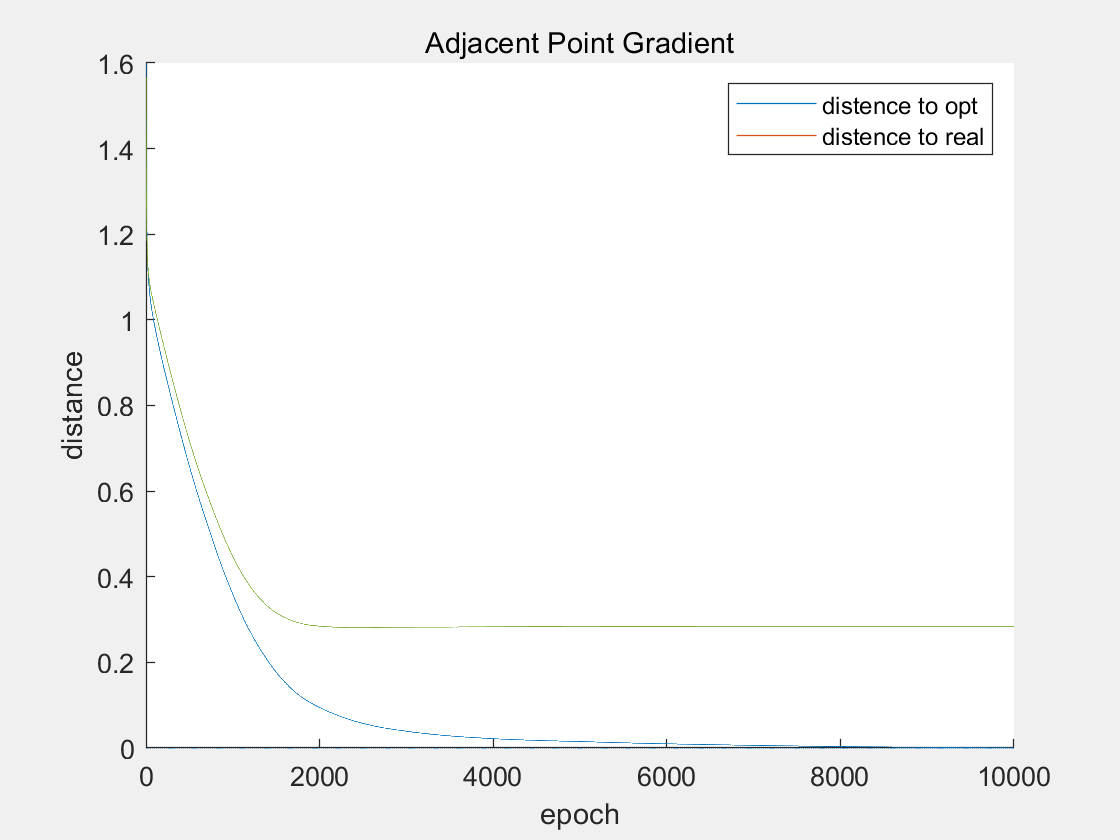
10000个epoches,历时 1.622360 秒。
交替方向乘子法
10000个epochs的图像由于抖动太大失真,具体可查看附件。
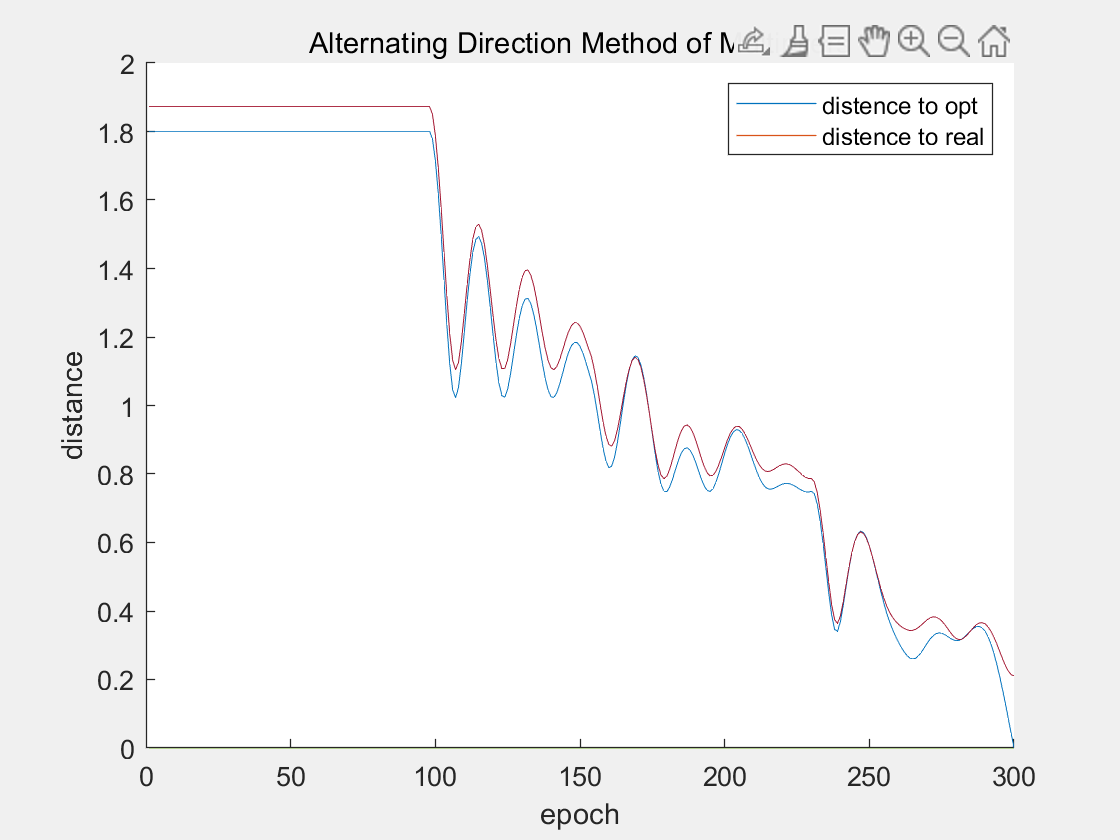
10000个epoches,历时 36.748212 秒。
次梯度法
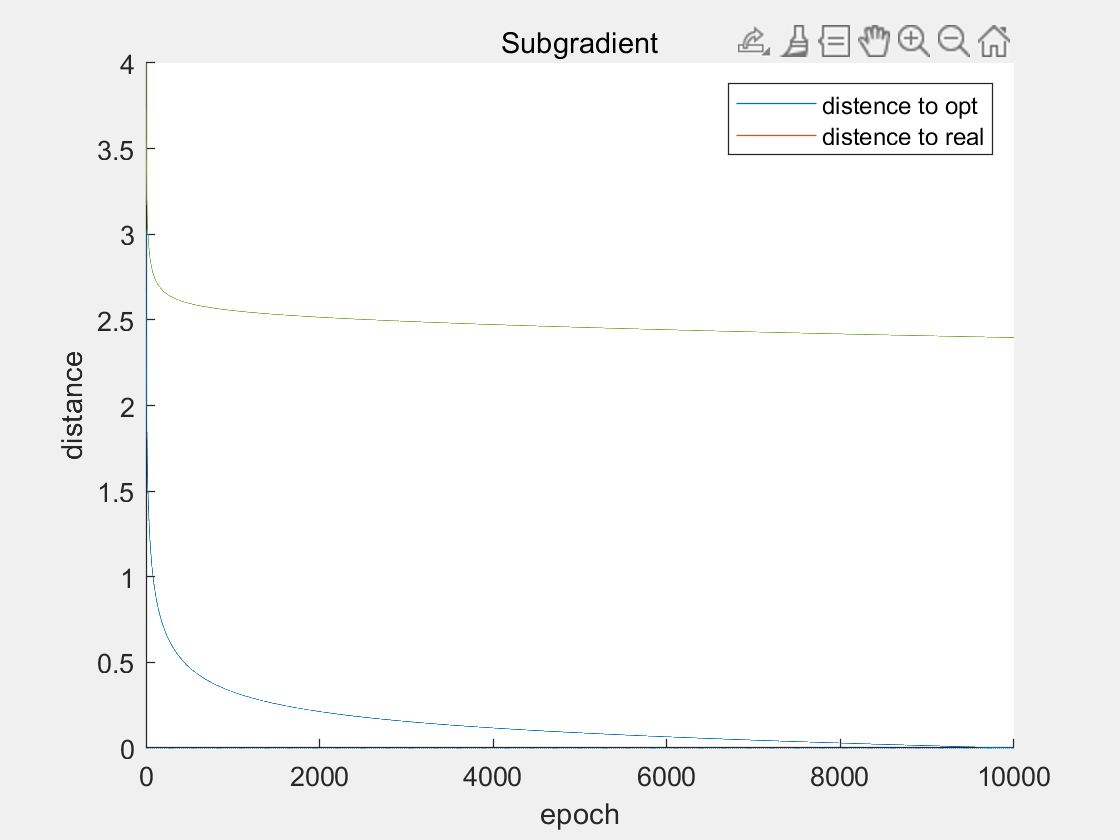
10000个epoches,历时 1.485966 秒。
1.4 结果分析
1.4.1 三种方法的比较



收敛性
在计算10000个epochs后,邻近点梯度法和交替方向乘子法均已收敛,而且均收敛在0.3附近。而次梯度法虽然也能够收敛,但是却收敛在2.5附近。
从理论上看,次梯度法在合适的步长下,能够收敛。但是缺点在于,次梯度法的计算结果会在最优解附近震荡,震荡的区间大小与步长有关。因此,从实验结果可以看出,在二范数的加持下,次梯度法求出的解与最优解的距离收敛到2.5左右,这与次梯度法本身以及步长密切相关。
而邻近点梯度法可以写成
\[x^{k+1}=x^k-\alpha\triangledown s(x^k)+\alpha\partial r(x^{k+1})\]其把次梯度的显式表示变为了隐式表示,从而使得解的收敛性更好。交替方向乘子法的收敛性也有有效的证明。
收敛速度
从收敛速度上来看,交替方向乘子法 优于 邻近点梯度法 优于 次梯度法。
在步长为 $\alpha^k=\frac{1}{\sqrt{k+1}}$ 时,次梯度法的收敛速度为 $O(\frac{\log k}{\sqrt{k}})$ 级别的,是次线性的收敛速度。
而邻近点梯度法在取合适的步长时,是线性的收敛速度。交替方向乘子法的收敛速度很难从理论上证明,但从效果上看,收敛速度也是很快的。
计算复杂度
同样执行10000个epochs,邻近点梯度法、交替方向乘子法、次梯度法分别历时 1.622360 秒、36.748212 秒、1.485966 秒。
抛开预处理、矩阵和向量的加减法、常量乘矩阵等复杂度不高的计算,比较三个方法的计算复杂度。
| 矩阵向量乘次数/轮 | 矩阵乘法次数/轮 | 10000轮用时 | |
|---|---|---|---|
| 邻近点梯度法 | 40 | 0 | 1.622360 秒 |
| 交替方向乘子法 | 20 | 0 | 36.748212 秒 |
| 次梯度法 | 40 | 0 | 1.485966 秒 |
乍一看好像交替方向乘子法的运算量更小。但是问题在于,$x$ 的每一轮更新为
\[x_i^{k+1}=(A_i^TA_i+cI)^{-1}(cz^k+A_i^Tb_i-\lambda_i^k)\]虽然已经将 $(A_i^TA_i+cI)^{-1}$ 预处理,但是每一轮计算的时候仍需要将该矩阵提取出来。这部分花费了36s中35s的时间,抛出这部分,其实三个算法的复杂度是大致相同的。
1.4.2 正则化系数
该部分使用邻近点梯度法进行比较,标准化系数如1.3.6所示。


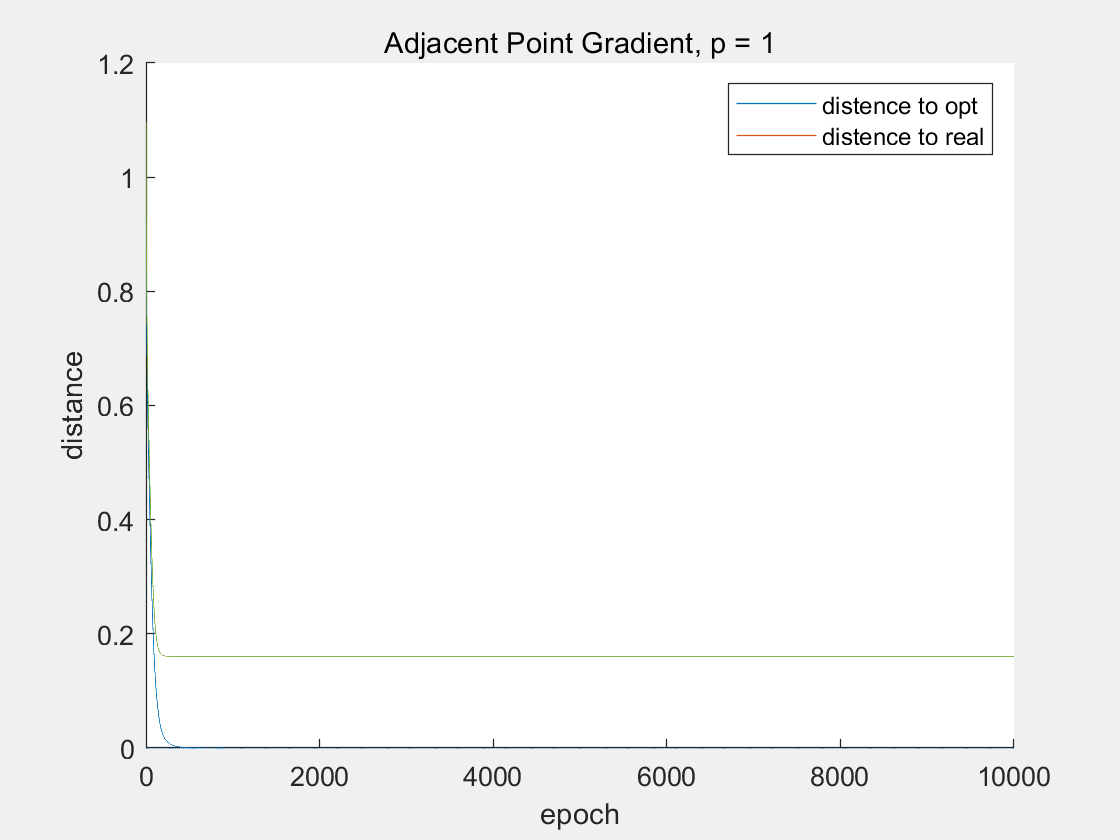
当 $p$ 越大时,实际收敛速度是越快的。这样比较无法看出有效结论。比较最优解的二范数和最优解的稀疏度(向量中0的个数)。
| p | 最优解的二范数 | 最优解的稀疏度 |
|---|---|---|
| 0.01 | 3.9584 | 0 |
| 0.1 | 3.9583 | 11 |
| 1 | 1.2594 | 21 |
| 10 | 1.2272 | 111 |
直观上看,当 $p$ 越大时,一范数对目标函数的影响也越大,因此最优解会朝着 0 向量的方向烟花。
对于一范数规范化最小二乘,已知一个结论,当正则化系数 $p>p_{max}$ 的时候,最优解必然为0。
可以简单证明,当
\[p_{max} = \max\lbrace\sum_{i=1}^{20}|A_{i,j}^Tb_i|\rbrace\]时,最优解必然为0。其中,$j$ 表示矩阵 A 的第 $j$ 列。因此,当 $p$ 越大时,最优解的稀疏度会越大,最优解的二范数会越小。
1.4.3 步长
该部分使用邻近点梯度法进行比较,标准化系数如1.3.6所示。

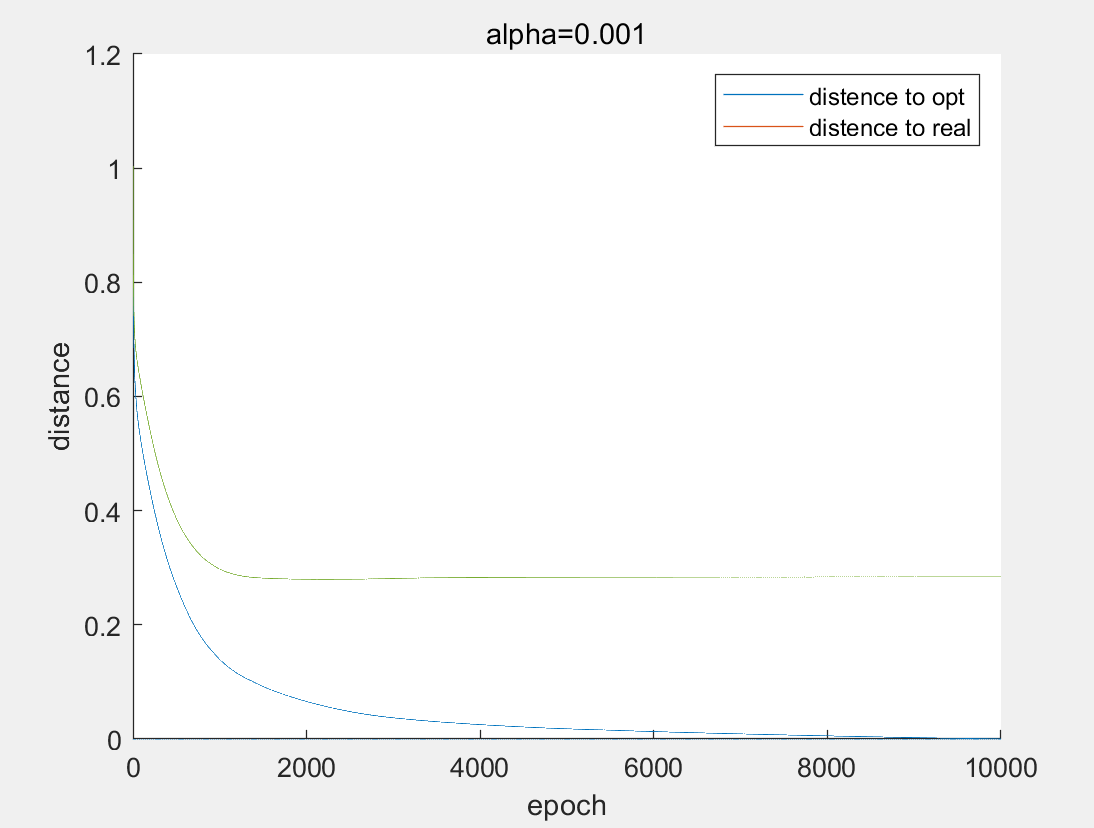

当步长为0.0001的时候,由于步长比较小,当迭代计算10000轮后,算法才慢慢开始收敛。
当步长为0.001的时候,步长设置比较合适,当迭代计算1000轮左右,算法已经开始收俩。
当步长为0.01的时候,由于步长太大,算法完全不收敛,发散到非常大的地方。
实验2 MNIST数据集分类
2.1 问题描述
请设计下述算法,求解 MNIST 数据集上的分类问题:
1、梯度下降法;
2、随机梯度法;
3、随机平均梯度法 SAG(选做)。
对于每种算法,请给出每步计算结果在测试集上所对应的分类精度。对于随机梯度法,请讨论 mini-batch 大小的影响。可采用 Logistic Regression 模型或神经网络模型。
2.2 算法设计
2.2.1 网络设计
对于图像处理,一般使用卷积神经网络。MNIST是一个很简单的数据集,图片大小为28x28,因此使用普通的卷积神经网络就能取得不错的效果。
网络的基本结构为两层的卷积层和一层的全连接层。
第一层的卷积层如下所示:
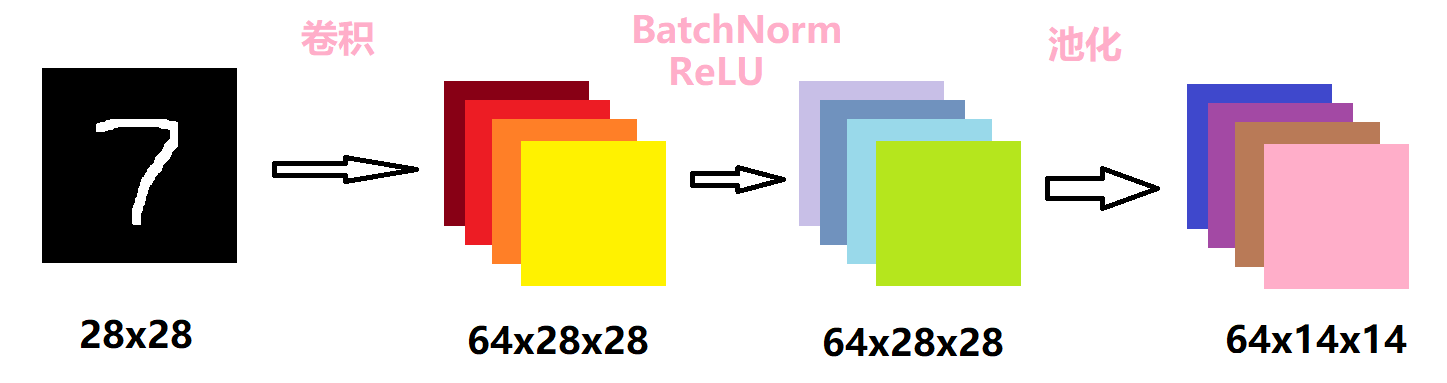
首先对原图像做一个卷积核大小为3的卷积操作。由于输入的图片是黑白图片,只有一个通道,因此卷积的输入通道为1,输出通道为64。设置了padding为1,而卷积核的大小是3,因此输出的维度会和输入的维度相同。
接着对卷积的结果做归一化操作后,经过一个ReLU激活函数,这两步不会改变数据的维度。选择ReLU的原因很简单,由于数据集很简单,而该激活函数本身的计算很简单,节约了计算成本。
最后再做一个kernel大小为2的池化操作,设置步长为2,因此数据大小会缩小一半。池化层的作用主要是下采样,可以降维、去除冗余信息、对特征进行压缩、简化网络复杂度、减小计算量、减小内存消耗等等。简单来说,就是减少计算量。
# net.py
# 第一层卷积层
self.conv1 = Sequential(
nn.Conv2d(in_channels=1, out_channels=64, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
接着再堆叠一层卷积层。
# net.py
# 第二卷积层
self.conv2 = Sequential(
nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(128),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
步骤是类似的,输入的维度是64x14x14,输出维度为128x7x7。
堆叠多层卷积层的原因是,则随着层次加深,提取的信息也愈加复杂、抽象。可以理解为,神经元一层一层的堆积后,对图片内容的理解会更加抽象和深刻。
最后需要经过一个全连接层,将这128x7x7维度的信息转换成我们需要的输出标签。具体的结构如下:
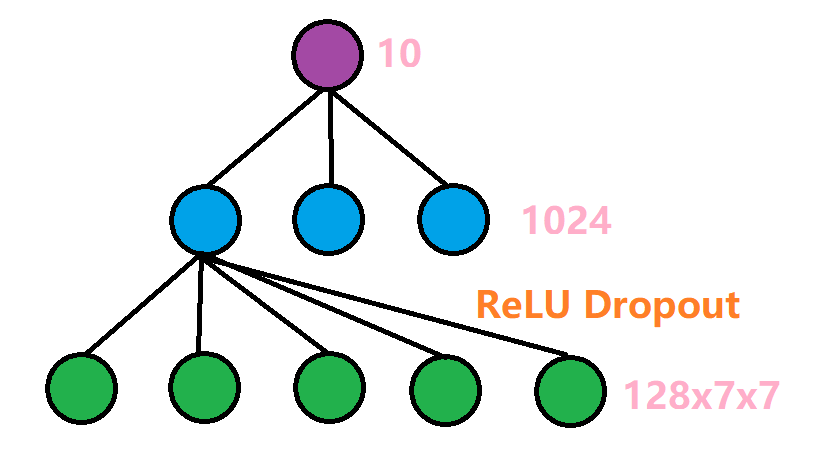
先由一个线性传播层,将128x7x7的信息转化为维度为1024的隐藏层,再经过ReLU激活函数,以及Dropout操作。Dropout操作是会随机选择一些单元丢弃,我们设置的概率为0.5,也就是会丢弃一般的信息,目的是为了防止过拟合。
# net.py
# 全连接层
self.dense = Sequential(
nn.Linear(7 * 7 * 128, 1024),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(1024, 10)
)
最后,将这三层网络堆叠起来,并重写一个前向传播函数,即可实现该网络结构。
# net.py
# 正向传播
def forward(self, x):
x1 = self.conv1(x)
x2 = self.conv2(x1)
x = x2.view(-1, 7 * 7 * 128)
x = self.dense(x)
return x
2.2.2 梯度下降法
梯度下降法表示为
\[x^{k+1}=x^k-\alpha^k\frac{1}{N}\sum_{i=1}^{N}\triangledown f_i(x^k)\]其中,$\alpha$ 表示步长。在本实验中,梯度的方向表现为损失函数,这里使用交叉熵函数:
\[\triangledown f_i(x)=-y_i\log \hat{y_i}\]其中,$y_i$ 为标签值,$\hat{y_i}$ 为预测值。
梯度下降法,即将所有训练数据使用梯度下降法进行训练。
if method == 'GD':
dataloader_train = DataLoader(dataset=data_train, batch_size=len(data_train)) # 训练集装载
dataloader_test = DataLoader(dataset=data_test, batch_size=len(data_test)) # 数据集装载
也就是说,加载数据集时,一个batch的大小为整个训练集。这样一次训练能够将所有数据进行梯度下降,并更新参数。
2.2.3 随机梯度法
随机梯度法表示为
\[x^{k+1}=x^k-\alpha^k\triangledown f_{i_k}(x^k)\]其中,$i_k$ 是第 $k$ 时刻选择的样本。那么,将训练数据划分为若干样本,每个样本的大小为 batch_size。
if method == 'SGD' or method == 'SAG':
dataloader_train = DataLoader(dataset=data_train, batch_size=batch_size, shuffle=True)
dataloader_test = DataLoader(dataset=data_test, batch_size=len(data_test), shuffle=True)
此时,使用 SGD 优化器便可实现随机梯度法。
if method == 'GD' or method == 'SGD':
optimizer = torch.optim.SGD(cnn.parameters(), lr=lr)
2.2.4 随机平均梯度法
随机平均梯度法的表达形式为
\[\begin{aligned} x^{k+1} &= x^k-\alpha\frac{1}{N}\sum_{i=1}^{N}y_{i_k}\\ y_{i_k} &= \left\lbrace \begin{aligned} \triangledown f_i(x^k)\ &,\text{if}\ i=i^k\\ y_{i_{k-1}}\ &,\text{其他} \end{aligned} \right. \end{aligned}\]此时,使用 ASGD 优化器便可实现随机梯度法。
if method == 'SAG':
optimizer = torch.optim.ASGD(cnn.parameters(), lr=lr)
2.3 数值实验
2.3.1 构建数据集及数据预处理
数据预处理
导入数据集的方式有很多。最简单的一种就是直接调用PyTorch封装好的函数。因为PyTorch里包含了 MNIST, CIFAR10 等常用数据集,调用 torchvision.datasets 即可把这些数据由远程下载到本地,下面给出MNIST的使用方法:
torchvision.datasets.MNIST(root, train=True, transform=None, target_transform=None, download=False)
- root 为数据集下载到本地后的根目录,包括 training.pt 和 test.pt 文件
- train,如果设置为True,从training.pt创建数据集,否则从test.pt创建。
- download,如果设置为True, 从互联网下载数据并放到root文件夹下
- transform, 一种函数或变换,输入PIL图片,返回变换之后的数据。
- target_transform 一种函数或变换,输入目标,进行变换。
因此,简单地使用datasets.MNIST即可导入训练集和测试集。
# 训练集导入
data_train = datasets.MNIST(root='data/', transform=transform, train=True, download=True)
# 数据集导入
data_test = datasets.MNIST(root='data/', transform=transform, train=False)
当然我觉得这么做很没有意思,我想自己看看这数据集是什么内容。于是我直接下载了该数据集,得到如下文件:

既然要手工处理,那首先得把二进制文件转换成既方便存储,又方便读取,我们还能够看得懂的文件,那么csv格式当仁不让。因此,实现了一个函数,用于读取二进制文件,并写入csv文件。
# utils.py
def convert(img_file, label_file, out_file, n):
'''
用于将数据集和标签转换成csv格式
img_file 数据集的路径
label_file 标签的路径
out_file 需要存储的csv的路径
'''
if os.path.isfile(out_file):
return
f = open(img_file, "rb")
l = open(label_file, "rb")
o = open(out_file, "w")
f.read(16)
l.read(8)
images = []
print("Generator " + out_file + " ...")
for i in tqdm(range(n)):
image = [ord(l.read(1))]
for j in range(28 * 28):
image.append(ord(f.read(1)))
images.append(image)
for image in images:
o.write(",".join(str(pix) for pix in image) + "\n")
f.close()
o.close()
l.close()
csv中的每一行都代表一个数据,其中第一维是标签,后面的28x28维是数据,也就是图片的像素值。csv的格式如下:
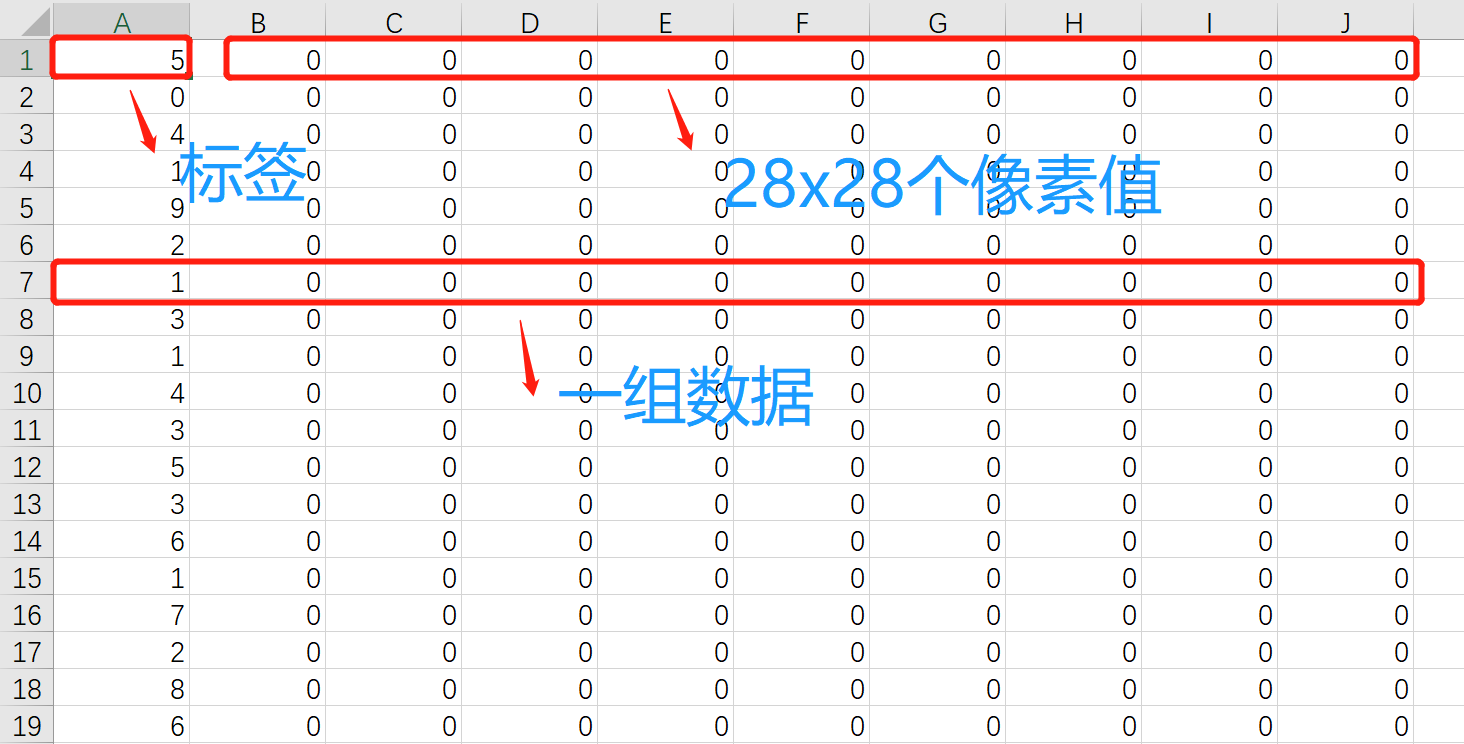
然后将数据集和测试集都进行转换:
# predata.convert_data()
convert(train_images_path, train_labels_path, data_path, 60000)
convert(test_images_path, test_labels_path, test_path, 10000)
得到如下结果:

接下来,我们可以采样一个数据,看看图片的内容。
# utils.py
def sample_data(source):
'''
用于采样一个数据集
source 数据集路径(csv)
'''
csv_file = csv.reader(open(source))
for content in csv_file:
content = list(map(float, content))
feature = content[1:785]
return feature
然后展示该图片:
# predata.convert_data()
feature = sample_data(data_path)
b = np.array(feature).reshape(28,28)
img = Image.fromarray(np.uint8(b))
img.show()
可以看到,由于是28x28的图片,图片非常小:
构建数据集
Pytorch提供了许多方法使得数据读取和预处理变得很容易。
torch.utils.data.Dataset是代表自定义数据集方法的抽象类,通过继承这个抽象类来定义数据集。一般来说,只需要定义__len__和__getitem__这两个方法就可以。
而通过继承torch.utils.data.Dataset的这个抽象类,定义好数据类后,我们需要通过迭代的方式来取得每一个数据,但是这样很难实现取batch,shuffle或者多线程读取数据,所以pytorch还提供了一个简单的方法来做这件事情,通过torch.utils.data.DataLoader类来定义一个新的迭代器,用来将自定义的数据读取接口的输出或者PyTorch已有的数据读取接口的输入按照batch size封装成Tensor,后续只需要再包装成Variable即可作为模型的输入。
因此, 我们首先需要定义两个Dateset,分别表示训练集和测试集:
# predata.py
class data_train(Dataset):
'''
train dataset
'''
def __init__(self):
self.x = load_data(data_path)
def __getitem__(self, idx):
assert idx < len(self.x)
return self.x[idx]
def __len__(self):
return len(self.x)
class data_test(Dataset):
'''
test dataset
'''
def __init__(self):
self.x = load_data(test_path)
def __getitem__(self, idx):
assert idx < len(self.x)
return self.x[idx]
def __len__(self):
return len(self.x)
其中,加载数据的部分如下:
# utils.py
def load_data(source):
csv_file = csv.reader(open(source))
data = []
for content in csv_file:
content = list(map(float, content))
feature = torch.tensor(content[1:785]).reshape(1,28,28)
feature = feature / 255 * 2 - 1
label = int(content[0])
data.append((feature, label))
return data
其中有很关键的一步,就是对数据进行归一化处理。由于输入像素的值域是0到255,而实际上我们希望数据服从均值为0,方差维1的分布。因此,手动实现了一个很简陋的归一化操作。当然,torchvision.transforms中有一个非常方便的方法可以处理:
transform = transforms.Compose([
transforms.ToTensor(), # 把数据转换为张量(Tensor)
transforms.Normalize( # 标准化,即使数据服从期望值为 0,标准差为 1 的正态分布
mean=[0.5, ], # 期望
std=[0.5, ] # 标准差
)
])
至此,数据集加载的整个流程已经完成。
# minist.py
convert_data() # 将数据集转换成csv
data_train = data_train() # 训练集导入
data_test = data_test() # 数据集导入
dataloader_train = DataLoader(dataset=data_train, batch_size=64, shuffle=True) # 训练集装载
dataloader_test = DataLoader(dataset=data_test, batch_size=64, shuffle=True) # 数据集装载
数据集加载完成后,我们可以浏览一下加载的数据,进行简单的核查:
# minist.py
images, labels = next(iter(dataloader_train))
img = make_grid(images)
img = img.numpy().transpose(1, 2, 0)
mean = [0.5, 0.5, 0.5]
std = [0.5, 0.5, 0.5]
img = img * std + mean
print([labels[i] for i in range(16)])
plt.imshow(img)
plt.show()
还原得到如下图像:
2.3.2 参数优化
参数优化
实例化网络后,首先进行GPU优化。使用GPU能显著提高训练速度。
# minist.py
cnn = CNN()
if torch.cuda.is_available(): # 判断是否有可用的 GPU 以加速训练
cnn = cnn.cuda()
接着设置损失函数。损失函数我们使用分类任务中最常用的交叉熵损失函数。
# minist.py
loss_F = nn.CrossEntropyLoss() # 设置损失函数为 CrossEntropyLoss(交叉熵损失函数)
2.3.3 训练和测试
整体训练和测试的框架为:
for epoch in range(epochs):
# 训练
# 测试
# 打印信息
这种架构能够直观地反应出,每次训练后的效果变化。
训练
首先我们设置训练的epoch的数量为10,学习率为0.01。
# env.py
epochs = 10
batch_size = 64
lr = 0.001
接下来结合代码进行解析:
# minist.py
# 训练
running_loss = 0.0 # 一个 epoch 的损失
running_correct = 0.0 # 一个 epoch 中所有训练数据的准确率
print("Epoch [{}/{}]".format(epoch, epochs)) # 打印当前的进度 当前epoch/总epoch数
for data in tqdm(dataloader_train): # 遍历每个数据,并使用tqdm反应训练进度
X_train, y_train = data # data是一个tuple,第一维是训练数据,第二维标签
X_train, y_train = get_Variable(X_train), get_Variable(y_train) # 将数据变成pytorch需要的变量
outputs = cnn(X_train) # 将数据输入进入网络,得到输出结果
_, pred = torch.max(outputs.data, 1) # 输出的结果是一个大小为10的数组
# 我们获取最大值和最大值的索引,后者表示预测结果
optimizer.zero_grad() # 梯度置零
loss = loss_F(outputs, y_train) # 计算输出结果和标签损失
loss.backward() # 根据梯度反向传播
optimizer.step() # 根据梯度更新所有的参数
running_loss += loss.item() # 累计全局的损失
running_correct += torch.sum(pred == y_train.data) # 计算准确率
测试
测试的操作和训练大同小异,直接获取测试集的数据,输入网络中得到结果,并与实际的标签进行比较。由于和训练部分类似,不做具体赘述。
# minist.py
# 测试
testing_correct = 0.0
for data in dataloader_test:
X_test, y_test = data
X_test, y_test = get_Variable(X_test), get_Variable(y_test)
outputs = cnn(X_test)
_, pred = torch.max(outputs, 1)
testing_correct += torch.sum(pred == y_test.data)
最后打印训练信息:损失值(反应训练的效果)、训练集准确度、测试集准确度。
# 打印信息
print("Loss: {:.4f} Train Accuracy: {:.4f}% Test Accuracy: {:.4f}%".format(
running_loss / len(data_train),
100 * running_correct / len(data_train),
100 * testing_correct / len(data_test))
)
之所以需要打印训练集准确度,通过对比测试集准确度,可以观察是否出现过拟合或者是网络设计不当的情况发生。
2.4 结果分析
2.4.1 梯度下降法
训练了3个epochs,模型基本收敛。三个epochs的交叉熵损失值、训练集准确度、测试集准确度如下:
Loss: 0.1747 Train Accuracy: 95.4383% Test Accuracy: 96.5700%
Loss: 0.0900 Train Accuracy: 97.6267% Test Accuracy: 97.7500%
Loss: 0.0797 Train Accuracy: 98.1067% Test Accuracy: 97.6100%
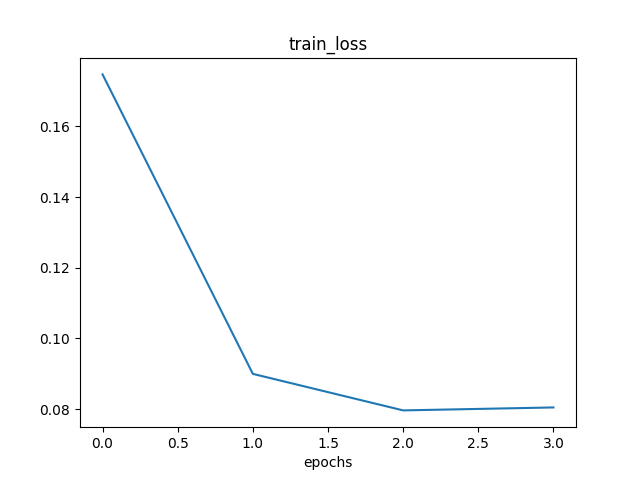
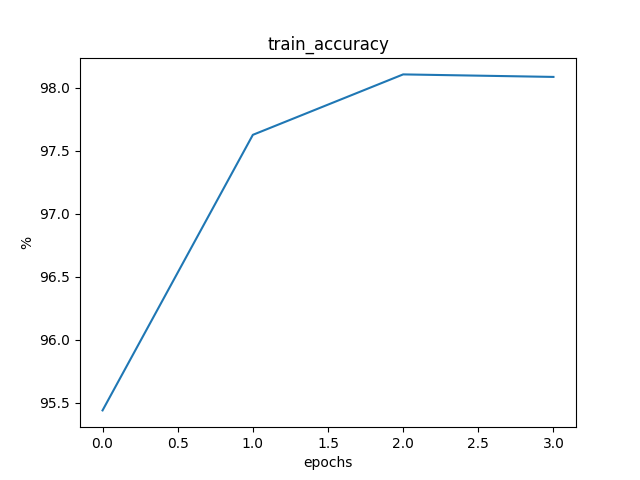
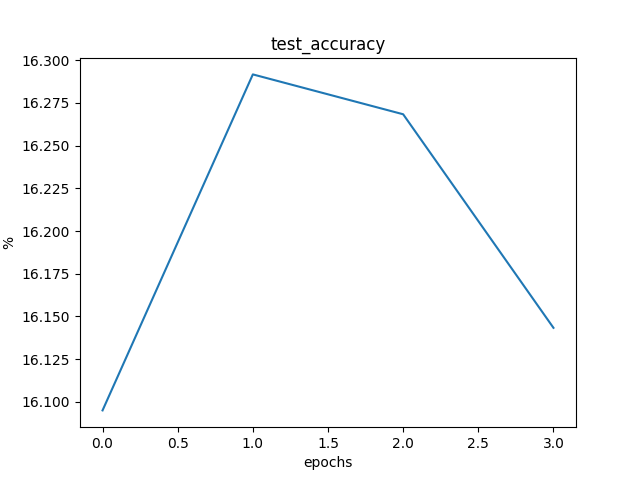
平均一个epoch的训练时间为 2:23:07。
2.4.2 随机梯度法
训练了 5000 个 epochs,模型收敛。对比了 mini-batch 大小分别为 32 和 64 的交叉熵损失值、训练集准确度、测试集准确度。具体的每个 epoch 的训练情况和比较转至 2.4.4 。
mini-batch为32的训练结果
训练至稳定状态,每 500 个 epochs 的训练信息如下:
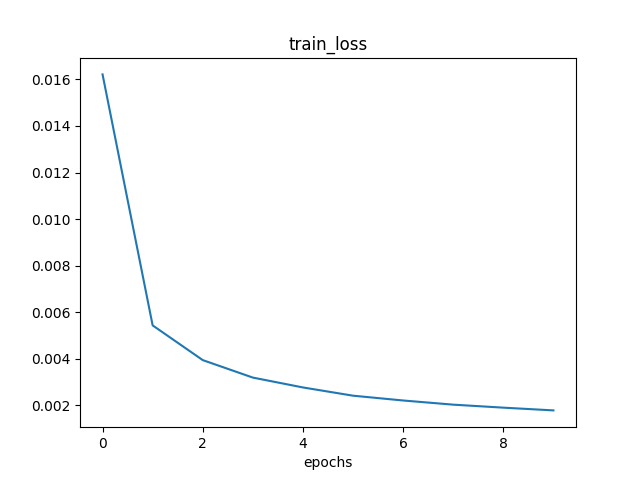
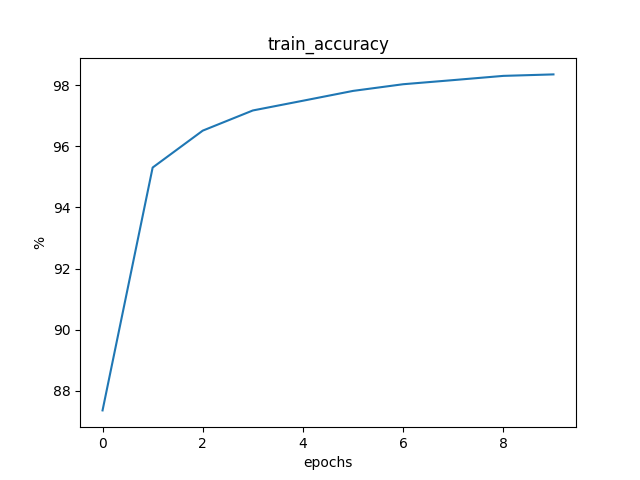
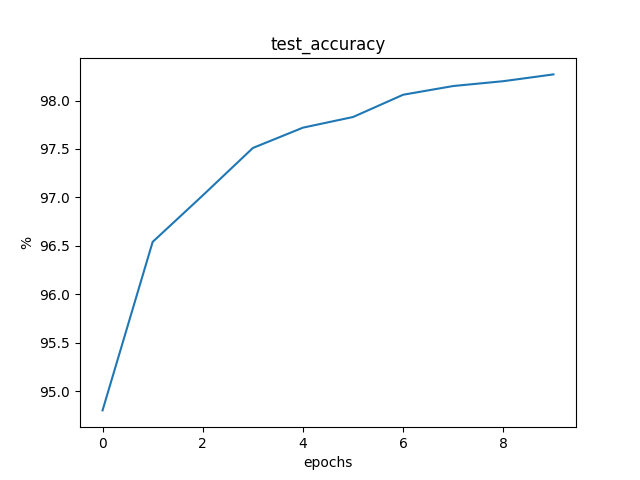
Loss: 0.0159 Train Accuracy: 87.6167% Test Accuracy: 94.7400%
Loss: 0.0055 Train Accuracy: 95.2383% Test Accuracy: 96.3200%
Loss: 0.0040 Train Accuracy: 96.5100% Test Accuracy: 97.1400%
Loss: 0.0032 Train Accuracy: 97.0883% Test Accuracy: 97.5800%
Loss: 0.0028 Train Accuracy: 97.4517% Test Accuracy: 97.8500%
Loss: 0.0025 Train Accuracy: 97.8000% Test Accuracy: 98.0300%
Loss: 0.0023 Train Accuracy: 97.9567% Test Accuracy: 97.9100%
Loss: 0.0021 Train Accuracy: 98.1033% Test Accuracy: 98.1900%
Loss: 0.0019 Train Accuracy: 98.2200% Test Accuracy: 98.4000%
Loss: 0.0018 Train Accuracy: 98.3533% Test Accuracy: 98.2700%
平均一个epoch的训练时间为 0.61s。
mini-batch为64的训练结果
训练至稳定状态,每 250 个 epochs 的训练信息如下:
Loss: 0.0115 Train Accuracy: 82.6217% Test Accuracy: 92.7500%
Loss: 0.0040 Train Accuracy: 93.3767% Test Accuracy: 94.8700%
Loss: 0.0029 Train Accuracy: 95.2083% Test Accuracy: 95.9600%
Loss: 0.0023 Train Accuracy: 96.0800% Test Accuracy: 96.6000%
Loss: 0.0020 Train Accuracy: 96.6150% Test Accuracy: 96.9600%
Loss: 0.0018 Train Accuracy: 96.8883% Test Accuracy: 97.3500%
Loss: 0.0016 Train Accuracy: 97.1967% Test Accuracy: 97.4200%
Loss: 0.0014 Train Accuracy: 97.4283% Test Accuracy: 97.5400%
Loss: 0.0013 Train Accuracy: 97.6300% Test Accuracy: 97.6600%
Loss: 0.0013 Train Accuracy: 97.7417% Test Accuracy: 97.8000%
平均一个epoch的训练时间为 1.332s。
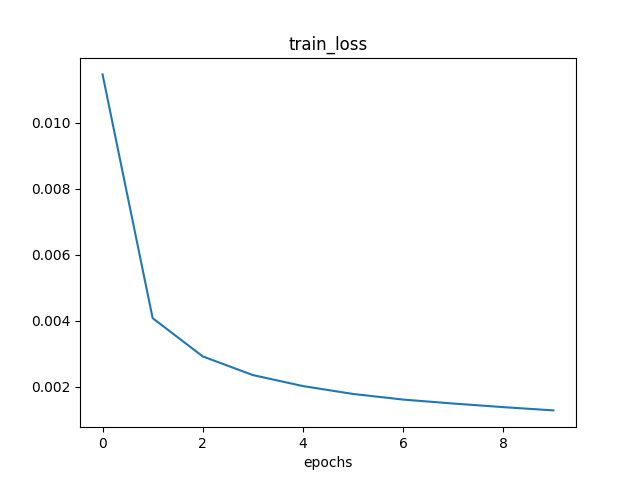

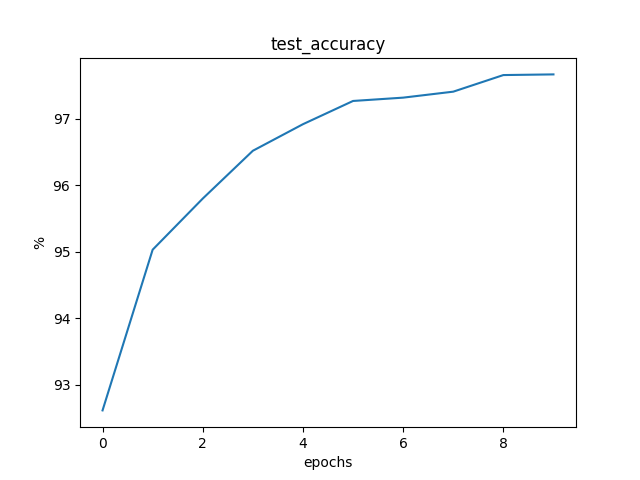
2.4.3 随机平均梯度法
训练了10个epochs,模型收敛。对比了mini-batch大小分别为32和64的交叉熵损失值、训练集准确度、测试集准确度。具体的每个 epoch 的训练情况和比较转至 2.4.4 。
mini-batch为32的训练结果
训练至稳定状态,每 500 个 epochs 的训练信息如下:
Loss: 0.0160 Train Accuracy: 87.6083% Test Accuracy: 94.7200%
Loss: 0.0056 Train Accuracy: 95.1817% Test Accuracy: 96.3200%
Loss: 0.0040 Train Accuracy: 96.3950% Test Accuracy: 96.8800%
Loss: 0.0033 Train Accuracy: 96.9900% Test Accuracy: 97.4800%
Loss: 0.0029 Train Accuracy: 97.3883% Test Accuracy: 97.7600%
Loss: 0.0025 Train Accuracy: 97.7717% Test Accuracy: 97.8200%
Loss: 0.0023 Train Accuracy: 97.8883% Test Accuracy: 98.0700%
Loss: 0.0021 Train Accuracy: 98.1150% Test Accuracy: 97.9900%
Loss: 0.0020 Train Accuracy: 98.1833% Test Accuracy: 98.2300%
Loss: 0.0018 Train Accuracy: 98.3167% Test Accuracy: 98.1700%
平均一个epoch的训练时间为 0.662s。
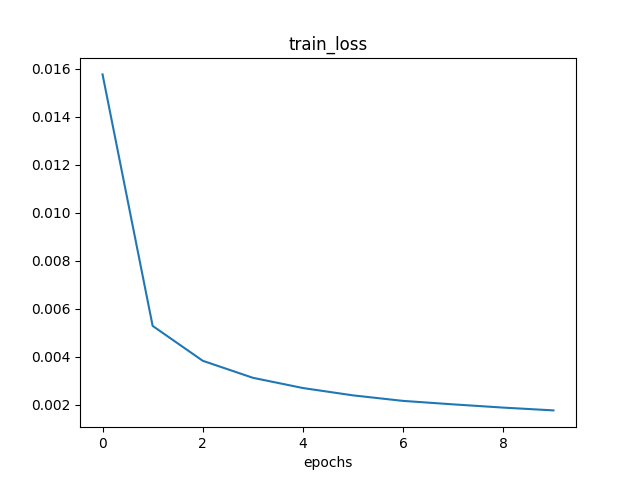
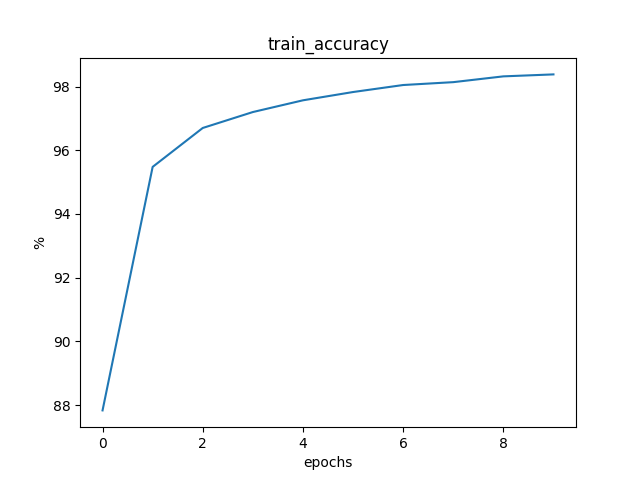
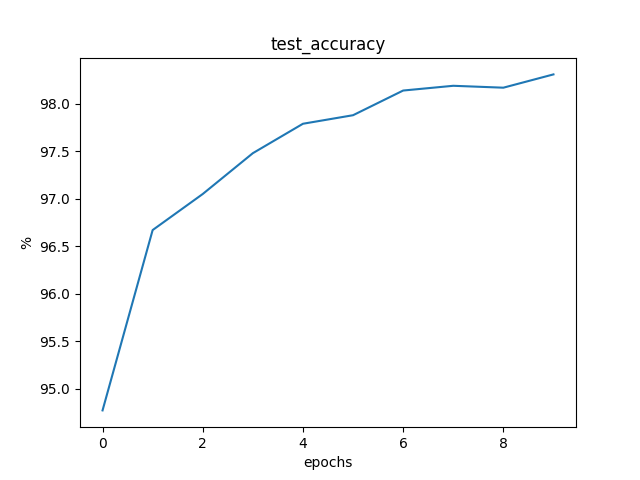
mini-batch为64的训练结果
训练至稳定状态,每 250 个 epochs 的训练信息如下:
Loss: 0.0117 Train Accuracy: 82.7167% Test Accuracy: 92.3200%
Loss: 0.0042 Train Accuracy: 93.1033% Test Accuracy: 94.6500%
Loss: 0.0030 Train Accuracy: 94.8617% Test Accuracy: 95.8700%
Loss: 0.0024 Train Accuracy: 95.8033% Test Accuracy: 96.2600%
Loss: 0.0021 Train Accuracy: 96.2750% Test Accuracy: 96.7100%
Loss: 0.0018 Train Accuracy: 96.7317% Test Accuracy: 97.1200%
Loss: 0.0016 Train Accuracy: 97.1117% Test Accuracy: 97.3200%
Loss: 0.0015 Train Accuracy: 97.3133% Test Accuracy: 97.4700%
Loss: 0.0014 Train Accuracy: 97.4900% Test Accuracy: 97.5000%
Loss: 0.0013 Train Accuracy: 97.6783% Test Accuracy: 97.5800%
平均一个epoch的训练时间为 1.22s。
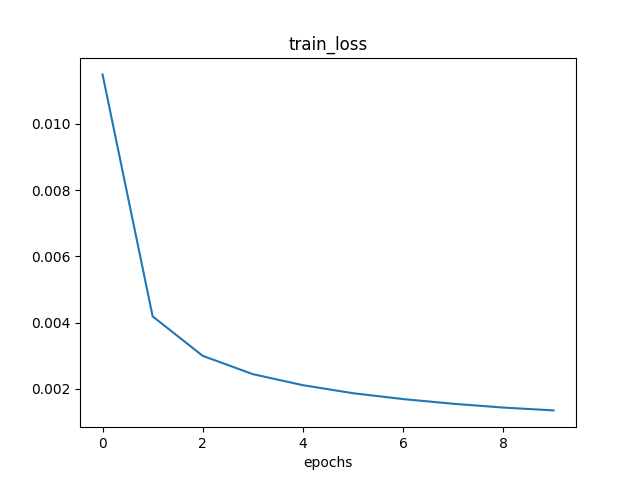
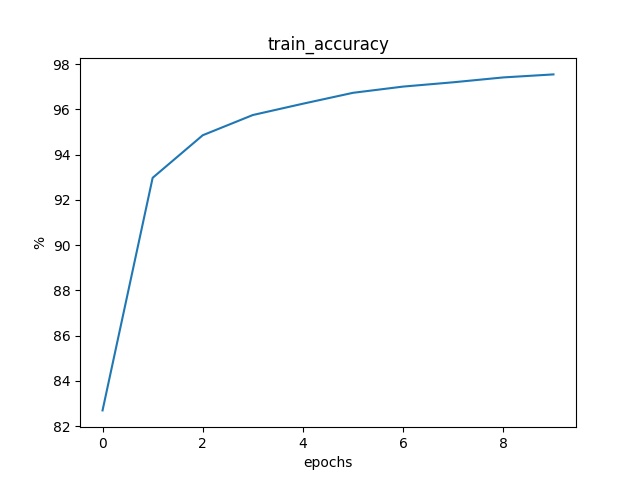

2.4.4 比较
训练时间
| 梯度下降法 | 随机梯度法 | 随机平均梯度法 | |
|---|---|---|---|
| 平均训练时间(epoch/s) | 2:23:07 | 跟batch大小有关 | 跟batch大小有关 |
大小为 32 的 mini-batch 的训练时间小于 1s。
可以看到,由于梯度下降法需要对所有训练数据进行计算,其训练时间要远大于后两者。而后两者算法的训练时间差别不大,在一个合理的波动范围中,符合预期。
| mini-batch | 32(500 epochs) | 64(250 epochs) |
|---|---|---|
| 随机梯度法 | 05:05 | 06:33 |
| 随机平均梯度法 | 05:31 | 06:05 |
当 mini-batch 变大时,每次计算的大小变大,因此训练时间也变长了,符合预期。
准确度
| 梯度下降法 | 随机梯度法 | 随机平均梯度法 | |
|---|---|---|---|
| 测试集准确度(平稳状态) | 97.6100% | 98.2700% | 98.1700% |
注:随机梯度法与随机平均梯度法的mini-batch大小为32。
| mini-batch | 32 (500 epochs) | 64 (250 epochs) |
|---|---|---|
| 随机梯度法 | 98.2700% | 97.8000% |
| 随机平均梯度法 | 98.1700% | 97.5800% |
理论上,当 mini-batch 变大时,每次计算的大小变大,训练的准确度也会上升了。实际上,当 mini-batch 大小为 64 的准确度达到 mini-batch 为 32 的训练准确度时,只花费了一半的训练轮数。因此,实际上随着训练轮数的增多,大小为 64 的 mini-batch 经过充分训练后可以达到 99% 以上的准确度。
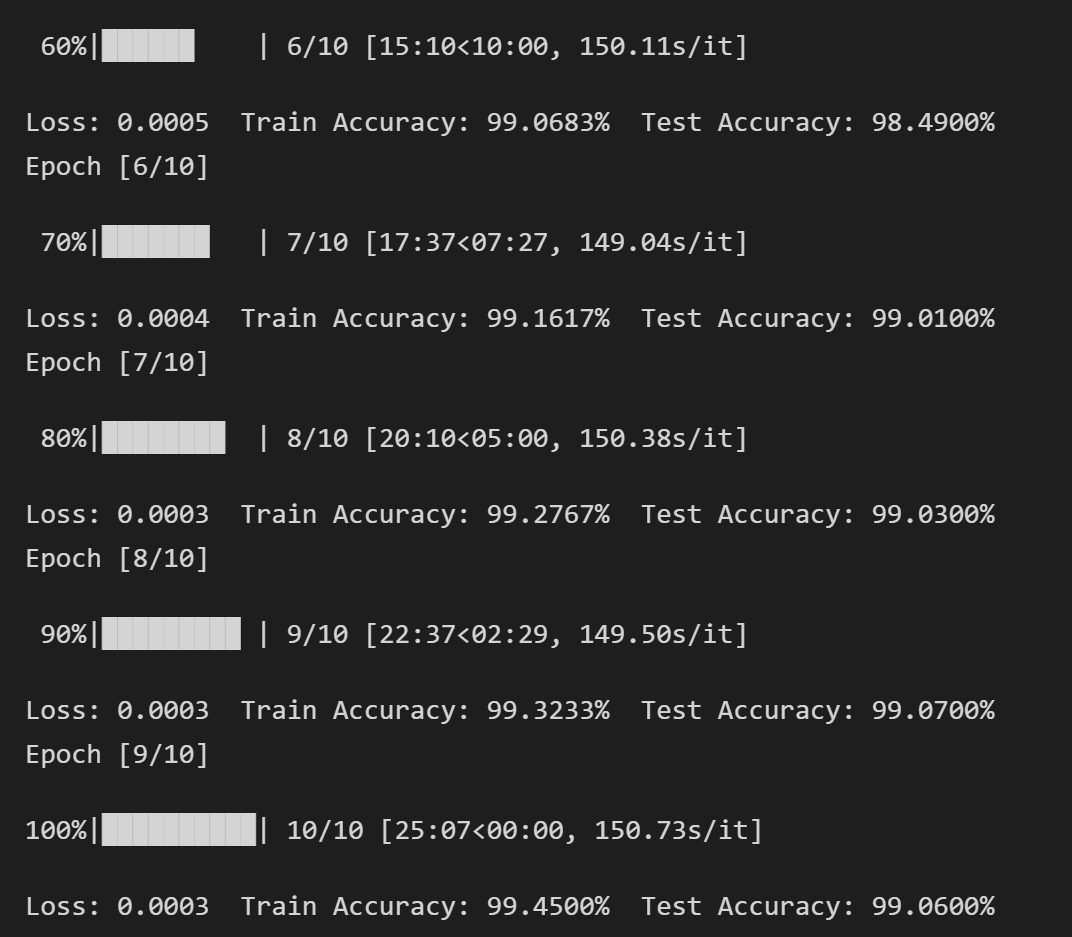
mini-batch 的影响
理论上
- 当batchsize太小时,相邻mini-batch间的差异太大,会造成相邻两次迭代的梯度震荡比较严重,不利于网络模型收敛;
- 当batchsize变大时,相邻mini-batch中的差异越小,梯度震荡会比较小,在一定程度有利于模型的收敛;
- 但是当batchsize极端大时,相邻mini-batch中的差异过小,两个相邻的mini-batch的梯度就没有区别,整个训练就按照一个方向一直走,容易陷入到局部最优。
实验中,抛开训练轮数看,训练 100 个 epochs 测试 mini-batch 对实验结果的影响。
具体每一轮的训练结果见 result\output_{method}_{batch_size}_100.txt。
| 算法 \ mini-batch | 1 | 32 | 128 |
|---|---|---|---|
| 随机梯度法 | 31.7100% | 69.7400% | 73.5800% |
| 随机平均梯度法 | 41.9800% | 70.2200% | 71.7900% |
可以看到,只训练 100 个 epochs
- 横向对比:当 mini-batch 越大的时候,训练的数据更多,测试集的准确度就越高。
- 纵向对比:由于随机平均梯度法使用了上一轮训练的信息进行梯度更新,因此其准确度会高于随机梯度法。
实验结果都在理论范围中。