BQ-NCO Bisimulation Quotienting for Efficient Neural Combinatorial Optimization

BQ-NCO:高效神经组合优化的双模拟分法（Bisimulation Quotienting不知道中文怎么翻译）

来自Naver Labs Europe

摘要

尽管基于神经的组合优化方法在端到端启发式学习中取得了成功，但分布外泛化仍然是一个挑战。在本文中，我们提出了一种新的组合优化问题(cop)作为马尔可夫决策过程(mdp)的公式，它有效地利用了cop的共同对称性来提高分布外鲁棒性。从一种构造方法的直接MDP公式出发，我们引入了一种基于MDP中的双模拟商(BQ)的通用方法来减少状态空间。然后，对于具有递归性质的cop，我们专门进行了双模拟，并展示了简化状态如何利用这些问题的对称性并促进MDP求解。我们的方法是有原则的，我们证明了所提议的BQ-MDP的最优策略实际上解决了相关的cop。我们举例说明了我们的方法在五个经典问题:欧几里得和非对称的旅行推销员，有能力的车辆路线，定向和背包问题。此外，对于每个问题，我们为bqmdp引入了一个简单的基于注意力的策略网络，我们通过模仿来自单个分布的小实例的(接近)最优解来训练它。我们在合成基准和现实基准上为五个cop获得了最新的最先进的结果。值得注意的是，与大多数现有的神经方法相比，我们学习的策略在没有任何额外搜索过程的情况下，对比训练期间看到的更大的实例表现出出色的泛化性能。我们的代码可在:url。

贡献

总而言之，我们的贡献如下：

我们提出了一个通用的和原则性的框架，可以在最低要求的情况下推导出任何COP的直接MDP;
我们提出了一种通过以对称为中心的双模拟引用来减少直接MDPs的方法，并定义了递归cop类的显式双模拟;
我们为bqmdp设计了一个适当的基于变压器的架构，仅对TSP(欧几里得和非对称版本)，CVRP, OP和KP进行了轻微的调整;
我们在这五个问题上实现了最先进的泛化性能，显著优于其他基于神经的构造方法。

CO as a MDP

定义了一个COP为，

\[\min_{x\in X}f(x)\]

$X$ 是有限非空可行解，$f$ 是目标函数。

解空间

解空间定义为 $(\mathcal{X},\circ,\epsilon,\mathcal{Z})$

$\mathcal{X}$ 是所有部分解的集合
$\circ$ 表示一种运算，$x\circ y$ 表示部分解 $x$ 的后面拼接部分解 $y$
$\epsilon$ 表示空解
$\mathcal{Z}\subset\mathcal{X}$ 表示一步解的集合

$\mathcal{X}$ 的任何元素都有有限正数的阶跃分解:

\[\forall x\in{\mathcal X},0<|\lbrace z_{1:n}\in{\mathcal Z}^{n}:x=z_{1}\circ\cdots\circ z_{n}\rbrace|<\infty.\]

直接MDP

直接MDP $\mathcal{M}_{(f,X)}$，

state space：$\bar{X}=\lbrace x{\in}{\mathcal X}:\exists y{\in}{\mathcal X},x{\circ}y{\in}X\rbrace$
action space：$\mathcal{Z}\cup\lbrace\epsilon\rbrace$
转移：

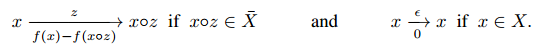
箭头上方表示动作，箭头下方表示奖励

$\mathcal{F}_{\mathcal{X}}$ 为 $(f,X)$ 实例的集合。

直接MDP满足三个性质：

动作有限
对于任何状态总存在一个可行动作
涉及阶跃作用的过渡次数是有限的

作者证明了这个直接MDP的完备性。

Bisimulation Quotienting

状态信息和对称性

作者观察，随着解的构造过程的推进，状态信息会越来越多，而动作空间会越来越小，这使得状态信息的复杂性和决策的复杂性不匹配（如构造TSP，已有解越来越长，包含的信息越来越多，但动作选择却越来越简单）。

因此，作者构造了一个规约算子

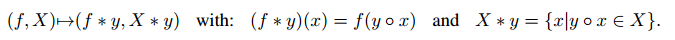
事实上，$(f\ast y,X\ast y)$ 是给定部分解 $y$ 后的尾部子问题。在TSP中，相当于给定了一个前缀解$y$，$y$的最后一个节点是$e$，尾部子问题相当于找到从$e$开始到仓库的一条路径。这样使得，只要子问题的尾部是$e$，且未访问的节点集合是一样的，那么问题就是对称的。

Bisimulation Quotiented MDP

根据规约算子，构造规约MDP $\mathcal{M}$：

状态空间：$\mathcal{F}_{\mathcal{X}}$
动作空间：$\mathcal{Z}\cup\lbrace\epsilon\rbrace$
转移

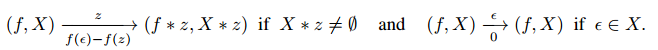
映射

\[\Phi_{(f,X)}{:}\bar{X}\mapsto\mathcal{F}_{\mathcal{X}}\]

是 $\mathcal{M}$ 和 $\mathcal{M}_{(f,X)}$ 的bisimulation（应该是叫做双模拟）。

形式上，$\mathcal{M}$ 通过双模拟与直接MDP的商同构，因此称为双模拟商(BQ-)MDP（Bisimulation Quotiented (BQ-)MDP）。

作者证明了BQ-MDP的完备性。

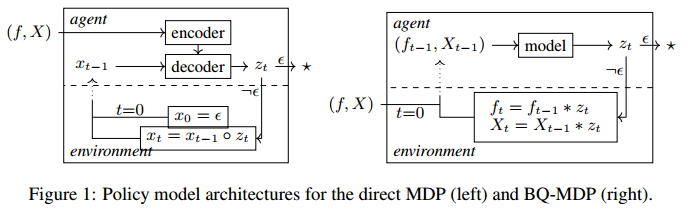
在模型结构上的作用

虽然直接和BQ-MDP在解决其相关COP方面是等同的，但它们的实际解释导致了重大差异。在直接MDP中，单独学习每个特定于实例的MDP是没有意义的。相反，学习基于输入实例的通用MDP，类似于目标条件强化学习。一个典型的策略模型架构由一个编码器和一个解码器组成，编码器负责计算输入实例的嵌入，解码器采用实例嵌入和当前的部分解决方案来计算下一个动作(图1左)，例如注意力模型或PointerNetworks。在轨迹的rollout中，编码器只需要调用一次，因为实例在整个rollout过程中不会更改。对于BQ-MDP，整个解空间只学习了一个无条件的MDP。该模型可以更简单，因为编码器和解码器之间的区别消失了(图1右)。另一方面，在rollout的每一步都必须将整个模型应用到一个新的输入实例。

实例参数化和递归

为了实现BQ-MDP，一个关键要求是 $(f\ast y,X\ast y)$ 可以在与 $(f, X)$ 相同的参数空间中表示。事实上，对于满足尾部递归属性的COP来说就是这样：在对实例应用了许多构造步骤之后，剩余的尾部子问题本身就是原始COP的一个实例。这是CO中一个非常常见的性质，特别是包括动态规划的最优性原则：所有适合动态规划的问题都满足尾递归性质。对于这些尾递归cop，双模拟只是将部分解映射到它所引起的尾子问题实例。

作者举例了背包问题和path-TSP（最短路径问题）。

策略学习

网络架构

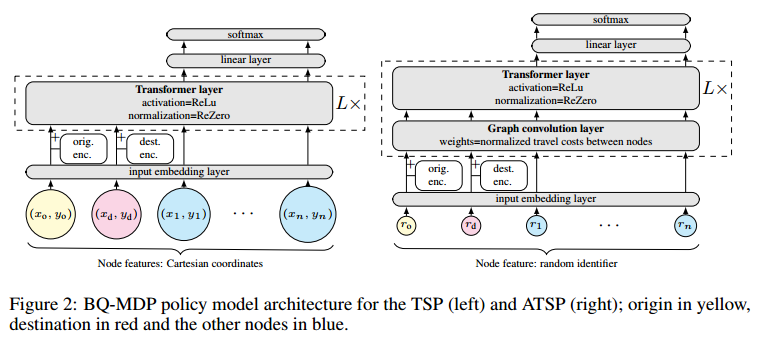
左侧是TSP，右侧是非对称TSP，$r_i$ 表示节点的标识嵌入。

轨迹生成

监督学习，交叉熵损失。

文章提到TSP和VSP可能的解不止一个，有一些是甚至是对称的，因此最优解不是直接以轨迹的形式出现的，即构造步骤的序列。

文章还提到固定轨迹解的任何子序列都可以解释为子实例的解。请注意，这些子实例在大小和节点分布上都是不同的，因此通过对它们进行训练，我们隐含地鼓励模型在大小和节点分布上都能很好地工作，并且比在训练期间没有看到这些变化时泛化得更好。

以上是省流版，感觉我没太搞懂，原文如下：

轨迹生成。我们通过模仿专家轨迹来训练我们的模型，使用交叉熵损失。这些轨迹是从预先计算的(接近)最优解中提取的，用于相对较小和固定大小的实例。即使对于困难的问题，我们也利用了这样一个事实，即通常可以有效地解决小实例(例如使用MILP求解器)。当然，学到的政策的质量将在更大的、因此更具挑战性的情况下进行评估。请注意，最优解不是直接以轨迹的形式出现的，即构造步骤的序列。虽然提案2保证任何解决方案都存在一个轨迹，但它通常不是唯一的。在TSP中，最优旅行对应于两个可能的轨迹(一个与另一个相反)。在CVRP中，每个子游类似地对应两个可能的轨迹，并且子游的不同顺序导致不同的轨迹。我们注意到这个最终顺序对性能有影响(见附录E.3)。另一方面，固定轨迹解的任何子序列都可以解释为子实例的解。请注意，这些子实例在大小和节点分布上都是不同的，因此通过对它们进行训练，我们隐含地鼓励模型在大小和节点分布上都能很好地工作，并且比在训练期间没有看到这些变化时泛化得更好。

复杂度

对于规模为 $N$ 的问题，模型的复杂度是 $O(N^3)$，使用的transformer的复杂度是 $O(N^2)$。复杂度的瓶颈在Transformer。

实验评估

问题：TSP、CVRP、OP、ATSP，附录中还有背包。

在100规模上训练，泛化到100、200、500、1k上评估，有合成数据集和标准数据集。

参数

9层Transformer，每层12个注意力头，监督学习，交叉熵损失。

TSP的解来自Concorde求解器，ATSP和CVRP是LKH，op是EA4OP启发式，数据集大小100w。

提到了上述没说明白的有多个解的问题，对每个实例，他提取了实例中的一些子节点构成子问题，得到了增强数据集。

为了从该数据集中采样轨迹，我们注意到，在TSP的情况下，最优巡回的任何子路径也是相关path-TSP子问题的最优解，因此适用于我们的path-TSP模型。因此，我们通过首先采样4到n之间的数字n(少于4个节点的path- tsp问题是平凡的)来形成小批量，然后从初始解集中采样长度为n的子路径。在每个epoch，我们从每个解中采样一个子路径。通过对最优解的所有可能中缀的子序列进行采样，我们自动得到一个增强的数据集，而以前的一些模型必须明确地为其设计模型。我们对CVRP、OP和KP使用了类似的采样策略。形成大小为1024的批次，并训练模型500次。我们使用Adam作为优化器，初始学习率为7.5e−4，每50次迭代衰减0.98。

baseline

与以下方法进行了比较:OR-Tools[37]、LKH[17]和Hybrid Genetic Search (HGS) for CVRP[44]作为SOTA非神经方法;DIFUSCO+2opt、at - gcn +MCTS和SGBS混合方法;AM、TransformerTSP、MDAM、POMO、DIMES和syn - nco是基于深度学习的构建方法。

结果

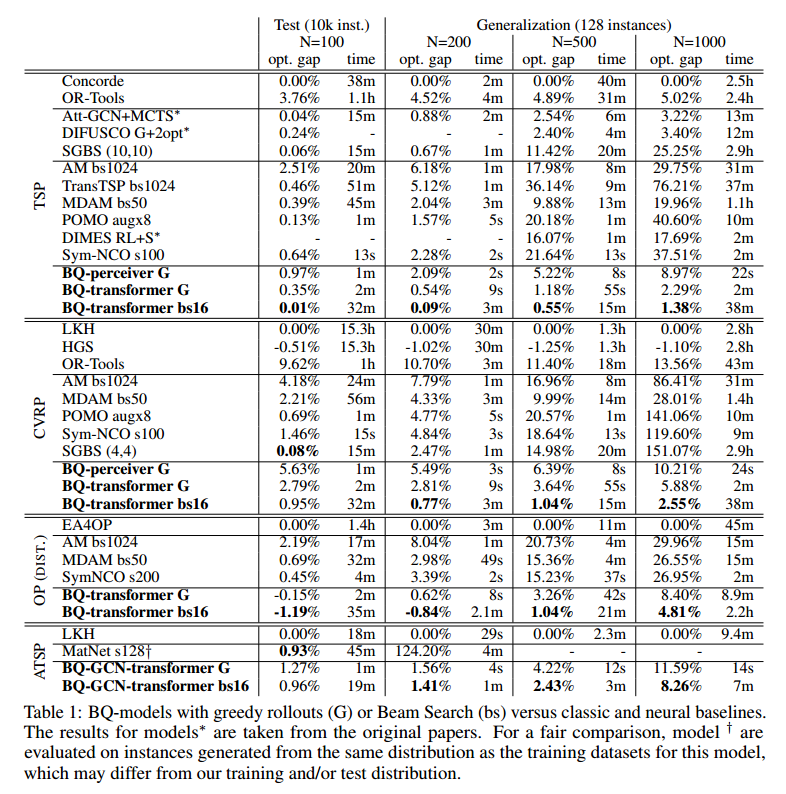
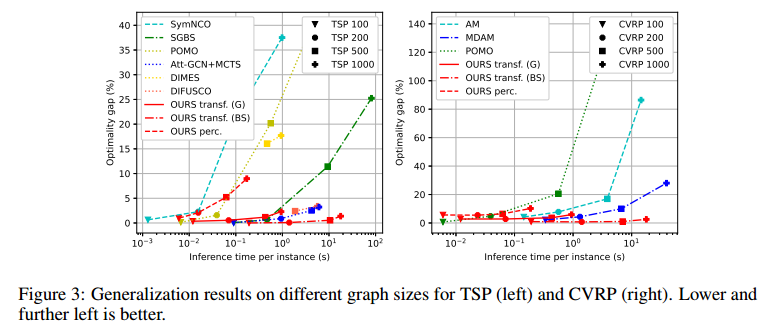
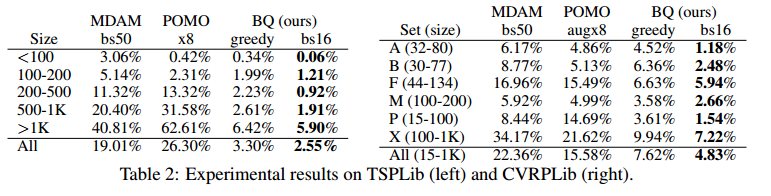
泛化性能很好，运行时间尚可。

总结

对于很容易确保解的可行性的问题还不错，但是对于约束比较多的问题就有挑战性。

将框架从确定性cop扩展到随机cop将特别有趣。

附录没看，附录里面特别多东西。