Winner Takes It All: Training Performant RL Populations for Combinatorial Optimization
赢家通吃:训练用于组合优化的高性能RL种群
来自InstaDeep
摘要
将强化学习(RL)应用于组合优化问题是有吸引力的,因为它不需要专家知识或预先解决的实例。然而,由于其固有的复杂性,期望智能体在一次推理中解决这些(通常是NP-)难题是不现实的。因此,领先的方法通常实现额外的搜索策略,从随机抽样和波束搜索到显式微调。在本文中,我们论证了学习一组互补策略的好处,这些策略可以在推理时同时推出。为此,我们介绍Poppy,一个简单的群体训练程序。Poppy没有依赖于预定义的或手工制作的多样性概念,而是引入了一种无监督的专业化,其目标仅仅是最大化群体的表现。我们证明Poppy产生了一组互补策略,并在四个流行的NP-hard问题上获得了最先进的RL结果:TSP、CVRP、0-1背包和作业车间调度。
省流
直接看3.2。
1 介绍
神经改进方法这种增量搜索不能快速访问非常不同的解决方案,并且需要手工编写过程来定义合理的操作空间。
神经构造方法在单次构造中效果不好,所以通常结合搜索策略。
作者提出了一种构造方法Poppy,该方法使用具有适当不同策略的代理群体来改进对硬CO问题解空间的探索。单个代理的目标是在整个问题分布中表现良好,因此必须做出妥协,而总体可以学习一组启发式方法,以便在任何给定的问题实例上只有其中一个必须表现良好。
挑战:(i) 训练一群智能体是昂贵的,并且难以扩展,(ii)训练的群体应该有提出不同解决方案的互补策略,以及(iii)鉴于缺乏与典型CO问题的性能相一致的明确行为标记,训练方法不应该在策略集内强加任何手工制作的多样性概念。
挑战(i)可以通过在整个种群中共享大部分计算来解决,只专门化轻量级策略头以实现代理的多样性。此外,这可以在预训练模型的基础上完成,我们可以克隆模型来产生种群。挑战(ii)和(iii)是通过引入一个RL目标来共同实现的,该目标旨在将代理专门用于问题分布的不同子集。具体来说,作者推导了一种针对群体水平目标的策略梯度方法,该方法对应于只训练在每个问题上表现最好的智能体。这在直觉上是合理的,因为在一个实例上训练一个代理,而另一个代理已经有更好的性能,这并没有提高总体在给定问题上的性能。
贡献总结如下:
-
我们鼓励使用种群来解决CO问题,作为一种有效的方法来探索不能通过单次推理可靠地解决的环境。
-
我们提出了一个新的培训目标,并提出了一个实用的培训程序,以鼓励绩效驱动的多样性(即不使用明确的行为标记或其他外部监督的有效多样性)。
-
我们在旅行推销员(TSP)、有能力车辆路径(CVRP)、0-1背包(KP)和作业车间调度(JSSP)四个CO问题上对Poppy进行了评估。在这四个问题中,Poppy始终优于所有其他基于强化学习的方法。
2 相关工作
ML for CO
- 利用典型CO问题(例如起始位置和旋转)的底层对称性,通过实例增强来实现改进的训练和推理性能。
- 使用了一种分层策略,其中播种者提出候选解决方案,由修订者逐位改进。
- 使用共享编码器和独立解码器训练多个策略。
- 给定当前解选择本地算子(2-opt)的策略。
- 通过随机采样学习策略来生成多样化的轨迹集,可能会使用额外的束搜索、蒙特卡罗树搜索、动态规划、主动搜索或模拟引导搜索。
基于群体的强化学习
- 使用以一组目标为条件的单一策略作为无监督技能发现的隐性群体。
- 显式存储一组不同的策略参数展开。
基于群体的强化学习的缺点之一是成本昂贵。
3 方法
3.1 背景和动机
RL表示
从分布 $\mathcal{D}$ 中采样出一个CO实例 $\rho$,包含了 $N$ 个节点。MDP如下:
-
状态 $\mathcal{S}$ :轨迹 $\tau_t=(x_1,\cdots,x_t)\in \mathcal{S}, x_i\in \rho$
-
动作 $a\in\mathcal{A}\subseteq \rho$
-
转移 $\tau_{t+1}=T(\tau_t,a)=(x_1,\cdots,x_t,a)$
-
奖励 $R:\mathcal{S}^\ast\to\mathbb{R}$
-
策略 $\theta$ :从概率分布 $\pi_\theta(\cdot\mid\rho,\tau_t)$ 选择一个动作,目标是最大化
梯度
\[\nabla_\theta J(\theta)=\mathbb{E}_{\rho\sim\mathcal{D}}\mathbb{E}_{\tau\sim\pi_{\theta},\rho}(R(\tau)-b_{\rho})\nabla_{\theta}\operatorname{log}(p_{\theta}(\tau))\]其中
\[p_{\theta}(\tau)=\prod_{t}\pi_{\theta}(a_{t+1}\mid\rho,\tau_{t})\]$b_\rho$ 是baseline。
动机
表述了多智能体比单智能体要好。
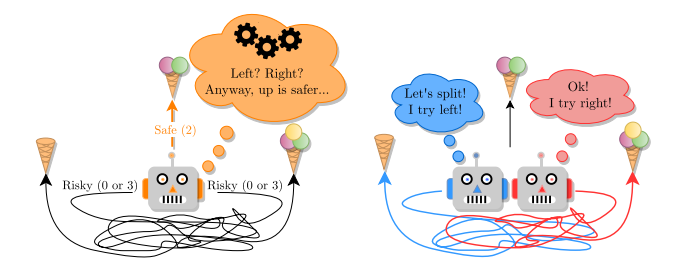
图1:在这个环境中,向上的路径总是通向中等奖励,而左右的路径是复杂的,任何一条路径都可能以相同的概率通向低奖励或高奖励。左图:一个被训练以最大化其预期奖励的智能体趋向于选择安全向上的道路,因为最优行为的计算量太大,因为它需要解决迷宫。右:2智能体群体总是可以选择左右两种路径,从而获得最大的奖励
我们用图1中的例子来说明训练人口的好处。在这个环境中,有三个操作:左、右和上。向上会导致中等奖励,而向左/向右则会导致低/高或高/低奖励(在每个情节开始时,配置的概率是相等的)。至关重要的是,左右路径错综复杂,因此代理不能轻易地从观察中推断出哪条路径会带来更高的奖励。然后,对于计算有限的智能体来说,最好的策略是总是向上,因为保证的中等奖励(2勺)高于猜测左或右的预期奖励(1.5勺)。相比之下,群体中的两个主体可以朝相反的方向前进,并且总是能找到最大的回报。有两个惊人的观察结果:(i)智能体不需要表现最优才能使总体表现最优(一个智能体获得最大奖励),以及(ii)每个个体智能体的表现比单智能体的情况更差。
3.2 Poppy
Poppy的组成部分:一个鼓励代理专业化的RL目标(RL objective encouraging agent specialization),以及一个利用预训练策略的有效训练过程。
假如有 $K$ 个策略 $\lbrace\pi_1,\cdots,\pi_K\rbrace$,群体目标是
\[J_{\mathrm{pop}}(\theta_{1},\ldots,\theta_{K})\doteq\mathbb{E}_{\rho\sim\mathcal{D}}\mathbb{E}_{\tau_{1}\sim\pi_{\theta_{1}},\ldots,\tau_{K}\sim\pi_{\theta_{K}}}\max\left[R(\tau_{1}),\ldots,R(\tau_{K})\right],\]梯度是
\[\nabla J_{\mathrm{pop}}(\theta_{1},\theta_{2},\ldots,\theta_{K})=\mathbb{E}_{\rho\sim\mathcal{D}}\mathbb{E}_{\tau_{1}\sim\pi_{\theta_{1}},\ldots,\tau_{K}\sim\pi_{\theta_{K}}}(R(\tau_{i})-R(\tau_{i^{\ast\ast}}))\nabla\log p_{\theta_{i^{\ast}}}(\tau_{i^{\ast}}),\]$\tau_{i^{\ast}}$ 是最优解,$\tau_{i^{\ast\ast}}$ 次最优解。这个梯度可以简单理解成,当最优解被移除后,性能变成了次优解,因此梯度是最优解减去次优解。
附录中有证明。
如果 $\theta_1=\theta_2=\cdots=\theta_K$,有
\[\nabla J_{\mathrm{pop}}(\theta)=\mathbb{E}_{\rho\sim\mathcal{D}}\mathbb{E}_{\tau_{1}\sim\pi_{\theta},\ldots,\tau_{K}\sim\pi_{\theta}}(R(\tau_{i^{\ast}})-R(\tau_{i^{\ast\ast}}))\nabla\log p_{\theta}(\tau_{i^{\ast}}),\]方法如下

训练分为两个阶段:
- 单智能体训练
- 克隆多个智能体训练
整体框架为
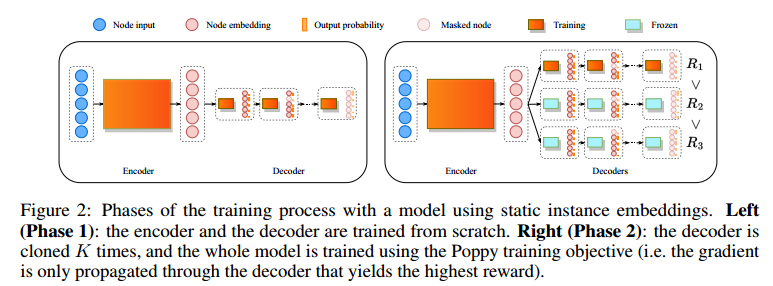
左图单智能体,右图多智能体。
为了减少总体内存,共享编码器。
实验
问题:TSP、CVRP、KP(背包)、JSSP
规模:100
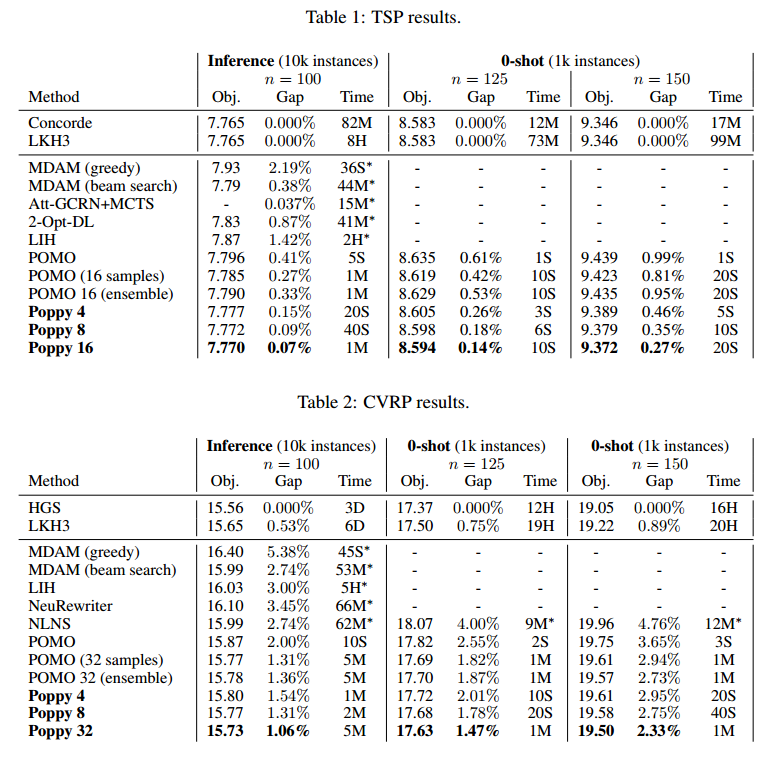
TSP和CVRP结果
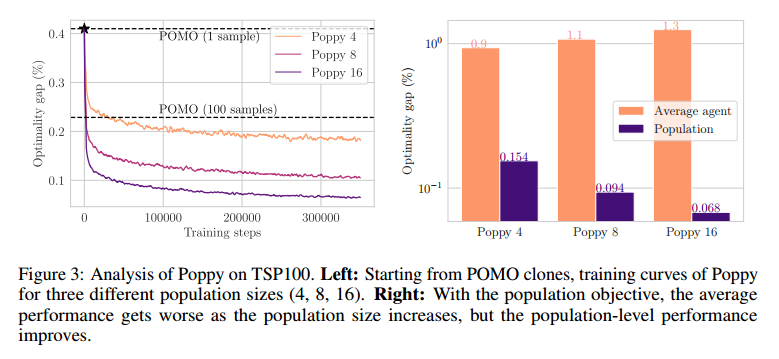
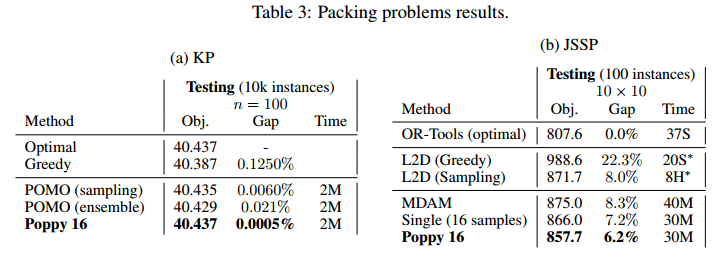
KP和JSSP结果
总结
将单目标多智能体引入RL。
但效果好像挺一般的。