Deep Reinforcement Learning for the Electric Vehicle Routing Problem With Time Windows
文章原文:https://ieeexplore.ieee.org/document/9520134
发表在2022 IEEE Transactions on Intelligent Transportation Systems
来自:多伦多大学、西伦敦大学等
题外话
这篇论文应该是第一篇用强化学习做EVRPTW,我没有调研过,不过我看着挺像的
我看最近几年还是有一些用启发式方法如分支定界、列生成做EVRPTW,甚至还有多目标的
我其实没有认真看这篇文章,只是作为CVRP的导入。
问题描述
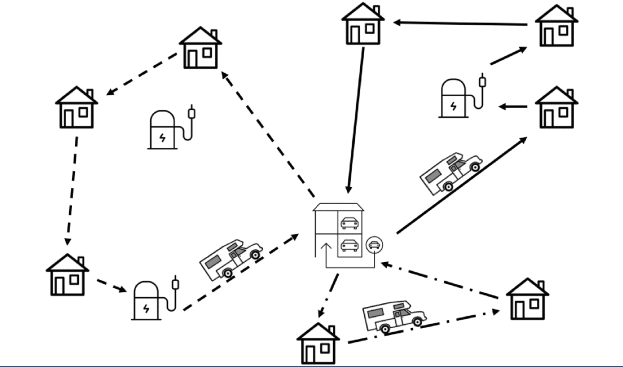
有三类节点:客户节点 $V_c$,充电站 $V_s$ 和仓库 $V_d$。
每个节点表示为 $X_i^t=(x_i,z_i,e_i,l_i,d_i^t)$
- $x_i,z_i$ 是二维平面坐标
- $e_i,l_i$ 是时间窗口,时间窗口最大范围是 $[0, T]$
- $d_i^t$ 表示在 $t$ 时刻车辆到节点 $i$ 的剩余需求
全局变量 $G^t=\lbrace\tau^t,b^t,ev^t\rbrace$
- $\tau^t$ 表示当前时间
- $b^t$ 表示当前电量
- $ev^t$ 表示有多少台车还在运行
一条轨迹 $\lbrace0,3,2,0,4,1,0\rbrace$ 表示两台电车的轨迹,一条是 $\lbrace0,3,2,0\rbrace$,另一条是 $\lbrace0,4,1,0\rbrace$。
强化学习表示
-
状态是 $X^t$ 和 $G^t$
-
动作是 $y^t$ 表示当前轨迹选择的一个节点,动作空间是 $Y^t$,终止时刻是$t_m$
-
策略是 $P(y^{t+1}\mid X^t,G^t,Y^t)$
-
转移
-
系统时间转移
\[\tau^{t+1}=\begin{cases}\max(\tau^t,e_{y^t})+s+w(y^t,y^{t+1}),&\mathrm{if~}y^t\in V_c\\\tau^t+re(b^t)+w(y^t,y^{t+1}),&\mathrm{if~}y^t\in V_s\\w(y^t,y^{t+1}),&\mathrm{if~}y^t\in V_d&\end{cases}\]如果 $t$ 时刻在客户节点,$\max(\tau^t,e_{y^t})$ 表示还没到 $y^t$ 的时间窗口起点就等待,$s$ 是服务时间,$w(y^t,y^{t+1})$ 是从 $y^t$ 到 $y^{t+1}$ 的旅行时间;如果 $t$ 时刻在充电,$re(b^t)$ 表示电量从 $b^t$ 到充满需要的时间; 如果当前时刻在仓库,意味是一辆新的车,只有 $w(y^t,y^{t+1})$。
-
电量转移
\[b^{t+1}=\begin{cases}b^t-f(y^t,y^{t+1}),&\mathrm{if~}y^t\in V_c\\B-f(y^t,y^{t+1}),&\mathrm{otherwise}&\end{cases}\]$f(y^t,y^{t+1})$ 是从 $y^t$ 到 $y^{t+1}$ 的电量消耗;从充电桩出发和从仓库出发都是满电的。
-
剩余车数和剩余需求
\[\begin{aligned} &ev^{t+1}= \left.\left\lbrace\begin{array}{ll}ev^t-1,&\mathrm{if~}y^t\in V_d\\ev^t,&\mathrm{otherwise}\end{array}\right.\right. \\ &d_i^{t+1}= \left.\left\lbrace\begin{matrix}0,&y^t=\mathrm{i}\\d_i^t,&\mathrm{otherwise}\end{matrix}\right.\right. \end{aligned}\]车数有限,一次需求全部解决
-
-
奖励:假设最终的路线是 $Y^{t_{m}}=\lbrace y^{0},y^{1},\ldots,y^{t_{m}}\rbrace^{k}$,奖励定义为
\[r(Y^{t_m})=-\sum_{t=1}^{t_m}w(y^{t-1},y^t)+\beta_1\max\lbrace-ev^{t_m},0\rbrace+\beta_2S(Y^{t_m})+\beta_3\sum_{t=0}^{t_m}\max\lbrace-b^t,0\rbrace\]- 第一部分是目标函数,总行驶距离越短越好,后面三个部分是惩罚,$\beta_{123}$ 都是负常数
- 第二部分是约束使用电车的数量不超标,超标了要惩罚
- 第三部分是约束尽可能少去充电,实在不行再去,作者说不加这个车会一直往充电桩跑
- 第四部分是约束尽可能不要透支电量
- 结论:这是软约束,不是硬约束
方法
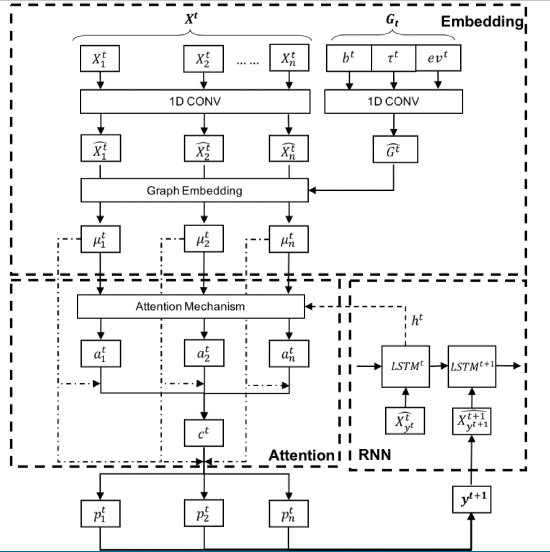
朴素的构造式强化学习,Transformr框架,编码器是self-attention,解码器是LSTM
解码器的mask机制
- 客户节点已经服务过了,或者载不下了就不去(我看他状态里面也没说车有容量上限)
- 电量不够去,或者去了不够回家
- 违反时间窗口终点约束
- 去了就无法在 T 时刻回家
- 如果当前在仓库,而且所有节点都服务完毕,就都不去
伪代码

值得思考的点
ECVRPTW,当然还有更复杂的,就是可以多次服务同一个节点,因为装不完分开装- 我搜这个问题的时候看到另一篇文章,不过我没有点进去看,他研究的是充电是否需要充满:https://www.mdpi.com/1996-1073/15/1/285
- 使用迭代改进式的方法