Ensemble-based Deep Reinforcement Learning for Vehicle Routing Problems under Distribution Shift
配送移位下基于集成的车辆路径问题深度强化学习

摘要
虽然在独立同分布情况下表现良好,但大多数现有的VRP神经方法在分布变化的情况下难以泛化。为了解决这个问题,我们提出了一种基于集成的vrp深度强化学习方法,该方法学习一组不同的子策略来应对不同的实例分布。特别是,为了防止参数收敛到同一参数,我们通过利用随机初始化的Bootstrap来强制子策略之间的多样性。此外,我们还通过在训练过程中利用正则化术语来明确追求子政策之间的不平等,以进一步增强多样性。实验结果表明,我们的方法在各种分布的随机生成实例上都能优于目前最先进的神经基线,并且在TSPLib和CVRPLib的基准实例上也有良好的泛化效果,证实了整个方法和各自设计的有效性。
贡献
- 经验证明,一个简单的类似子策略集合导致求解具有分布移位的vrp的性能有限。
- 提出了一种基于集成的深度强化学习(EL-DRL),其基于集成的策略梯度允许多个子策略学习协作地利用各自分布上的优势。通过将不同的损失信号分配给子策略并基于不等式度量应用正则化来促进多样性。
- EL-DRL在各种分布的实例上自适应地训练子策略,并且无需手动指定实例类或组即可灵活地训练每个子策略。
- 将POMO作为EL-DRL中的子模型,用于在各种分布的合成和基准实例上解决旅行推销员问题(TSP)和有能力车辆路线问题(CVRP)。结果验证了EL-DRL具有良好的交叉分布泛化性。
相关工作
-
VRP的深度学习方法
-
深度集成学习(Deep Ensemble Learning)
没听过这个概念,遂去调研了一番
集成学习:通过构建并结合多个学习器来完成学习任务
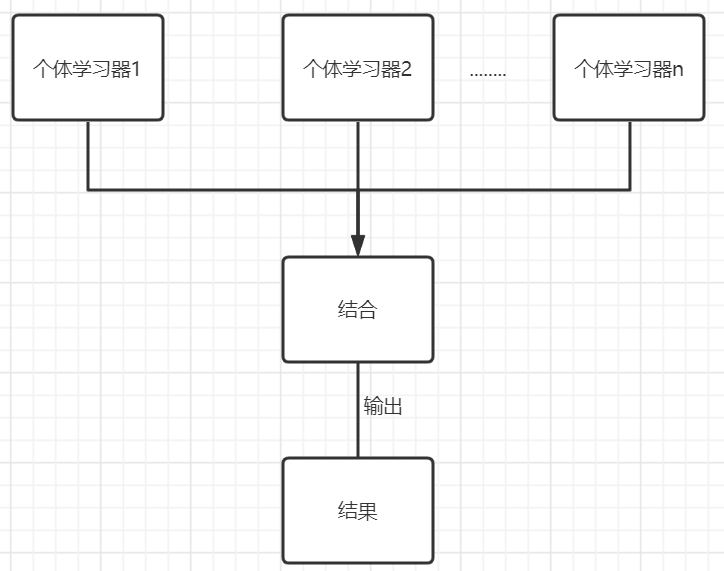
同质:个体学习器是同一个类型(一般是用这个)
异质:学习器包含不同类型
个体分类器需要满足
- 具有一定的性能,起码不能比随机差
- 个体分类器之间要有差异,不能都一样,多样性
分类:
- Boosting:个体学习器之间存在强依赖,需要串行
- Bagging:我个人认为只是单纯的并行
- Stacking:一些神经方法
Boosting
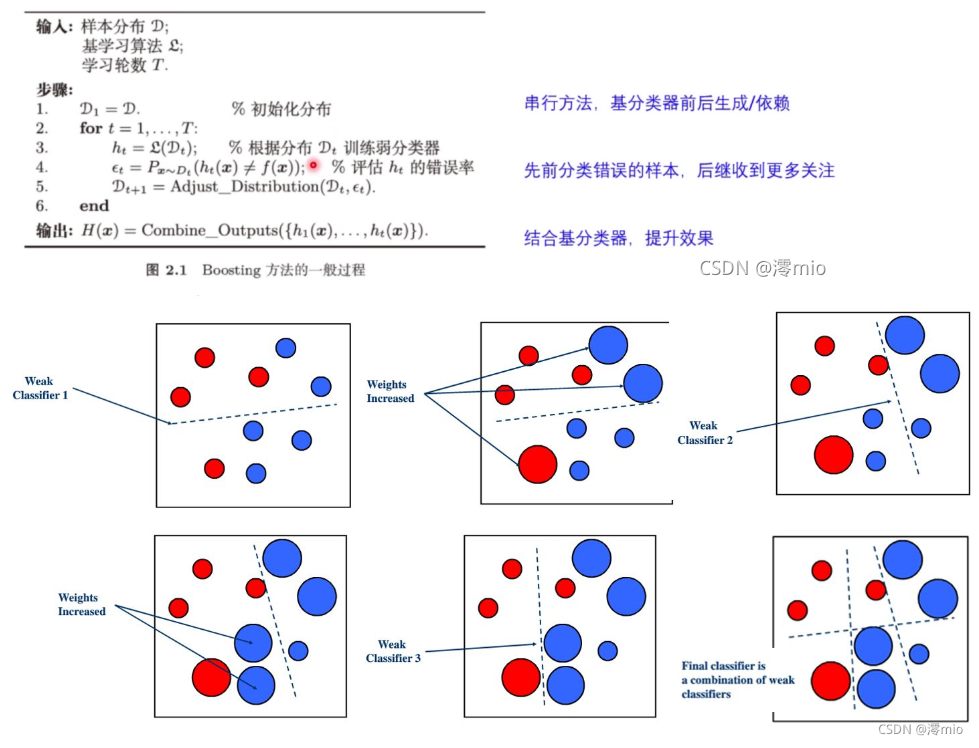
Bagging
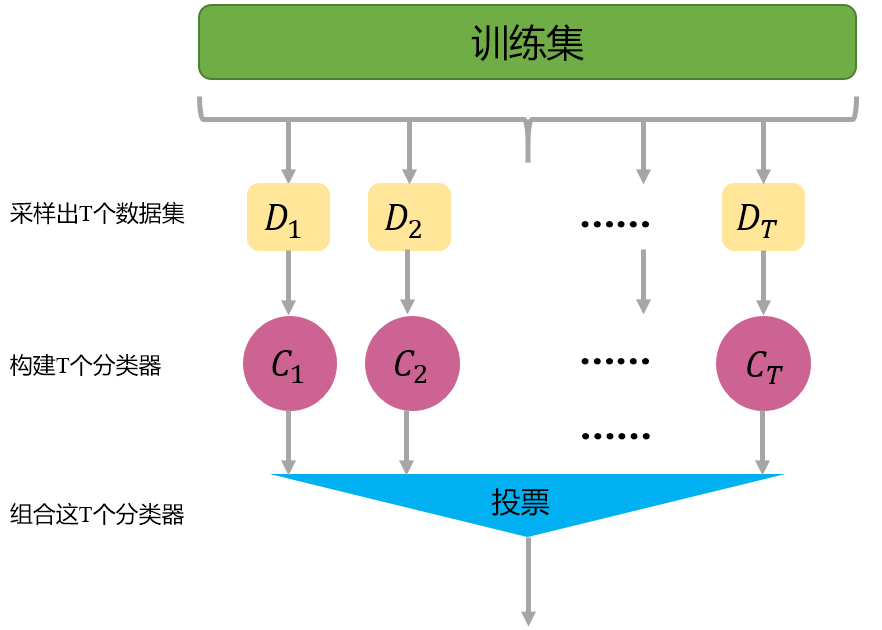
综述:https://arxiv.org/pdf/2104.02395.pdf
译文:https://zhuanlan.zhihu.com/p/465127883
参考资料:https://blog.csdn.net/qq_52358603/article/details/121106562
-
MDAM
MDAM利用配备多个解码器的AM来解决vrp,每个解码器对应于集成学习中的一个子模型。
encoder-decoder框架,强化学习
编码器:GNN
解码器:
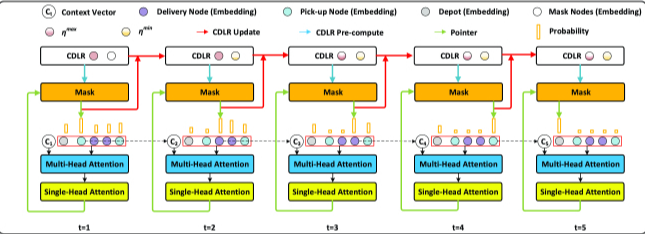
第一个注意力层通过多头机制计算上下文嵌入,该机制可使模型整合来自不同子空间的信息。第二层利用单头机制计算选择节点的概率。
论文:https://dl.acm.org/doi/10.1145/3546952
-
L2I
计算开销大
方法
基于集成的策略梯度
EL-DRL基于一个猜想,在基于集成的学习范式中,神经网络参数的高相似性与较差的性能相关。
在POMO的基础上构建EL-DRL,但是这个方法是通用的,也可以在提起神经启发式方法上面适配。
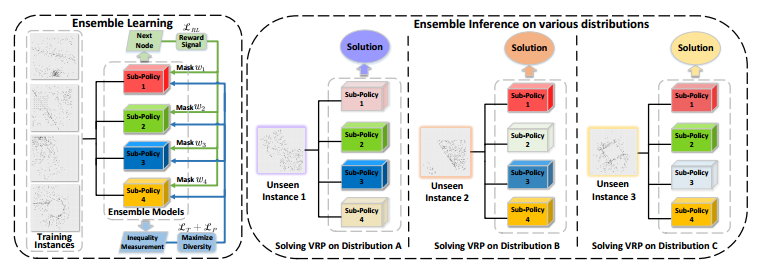
EL-DRL结构:它使用各自的屏蔽奖励(强化损失)信号和不等式正则化来训练子策略以最大化多样性。在推理过程中,子策略通过利用它们在不同分布上的优势进行协同。不同程度的透明度表明每个子政策在得出解决方案时的贡献不同。
具体来说,配备了 $M$ 个子策略网络,每个策略网络都是一个POMP。策略网络可以表示成 $\pi_\theta$,对于一个大小为 $N$ 的实例,一个策略网络可以得到一组解的轨迹, $\lbrace\tau^1,\tau^2,\cdots,\tau^N\rbrace$ ,并且可以得到其奖励 $R(\tau^i)$。对于一个策略网络,其强化学习的目标是
\[\mathcal{L}=\mathbb{E}_{\tau^1 \sim \pi_\theta} R\left(\tau^1\right) \mathbb{E}_{\tau^2 \sim \pi_\theta} R\left(\tau^2\right) \ldots \mathbb{E}_{\tau^N \sim \pi_\theta} R\left(\tau^N\right)\]那么对于 $M$ 个子策略网络,其目标是
\[\nabla \mathcal{L}(\theta \mid s) \approx \frac{1}{N M} \sum_{i=1}^N \sum_{m=1}^M\left(R\left(\tau_m^i\right)-b(s)\right) \nabla \log \pi_\theta^m\left(\tau_m^i \mid s\right)\]其中,$\pi_\theta^m\left(\tau_m^i \mid s\right)$ 是第 $m$ 个策略网络在给出 $s$ 的状态下,选择动作 $\tau_m^i$ 的概率。
但是这样会导致一个问题,由于所有子策略获得相同的奖励,结构也是类似的,因此很可能会导致参数收敛相同。
解决办法,采用随机初始化的Bootstrap来训练子策略网络集合,通过两种措施促进子网络的多样性:
-
初始化时具有不同的随机参数的解码器,初始多样性
-
不同的强化损失信号,即在对于每个策略网络,将一个服从参数 $\beta\in(0,1)$ 的伯努利分布的二进制掩码 $w_i^m$ 应用到奖励函数上,得到
\[\nabla \mathcal{L}_{R L}(\theta \mid s) \approx \frac{1}{N M} \sum_{i=1}^N \sum_{m=1}^M w_m^i\left(R\left(\tau^i\right)-b(s)\right) \nabla \log \pi_\theta^m\left(\tau^i \mid s\right)\]其中,baseline是
\[b(s)=\frac{1}{N M} \sum_{i=1}^N \sum_{m=1}^M R\left(\tau_m^i\right)=\frac{1}{N} \sum_{i=1}^N R\left(\tau^i\right)、\]
通过正则化增强多样性
为了提高策略网络的多样性,作者利用正则化来鼓励子策略网络的显示多样性。
-
利用Theil指数
在经济学中,Theil指数用来表示区域经济差异状况,数值越大则差异程度越大
Theil指数在损失函数中表现为
\[\mathcal{L}_T=\frac{1}{M} \sum_{m=1}^M \frac{x_m}{\mu} \ln \frac{x_m}{\mu}\]其中,$x_m$ is the $\ell^2$-norm of $\theta_m$ and $\mu$ is the mean of all $\ell^2$-norms.
-
共识优化原理,施加惩罚阻止所有子策略收敛到同一个值
\[\mathcal{L}_P=\sum_{m=1}^M\left\|\bar{\theta}-\theta^m\right\|^2\]where $\bar{\theta}$ is the mean of the parameters for all sub-policies.
最后,损失函数会变成
\[\nabla \mathcal{L} \approx \mathcal{L}_{R L}(\theta \mid s)-\alpha_1 \mathcal{L}_T-\alpha_2 \mathcal{L}_P\]在推理阶段,EL-DRL通过旋转对每个输入实例进行扩充,并从所有节点的每个节点开始,协同贪婪地产生多条轨迹。最终解被指定为所有采样轨迹中的最佳解。
实验
数据集:合成TSP和CVRP实例、benchmark TSPLib和CVRPLib
baseline:注意力模型(AM),多重最优策略优化(POMO),多解码器注意力模型(MDAM), POMO分布鲁棒优化(DROP),硬度自适应课程(HAC)和自适应多分布知识蒸馏(AMDKD)
实现:一个编码器和四个解码器
训练集大小:720w,测试姐大小:2000 x 5
实验结果
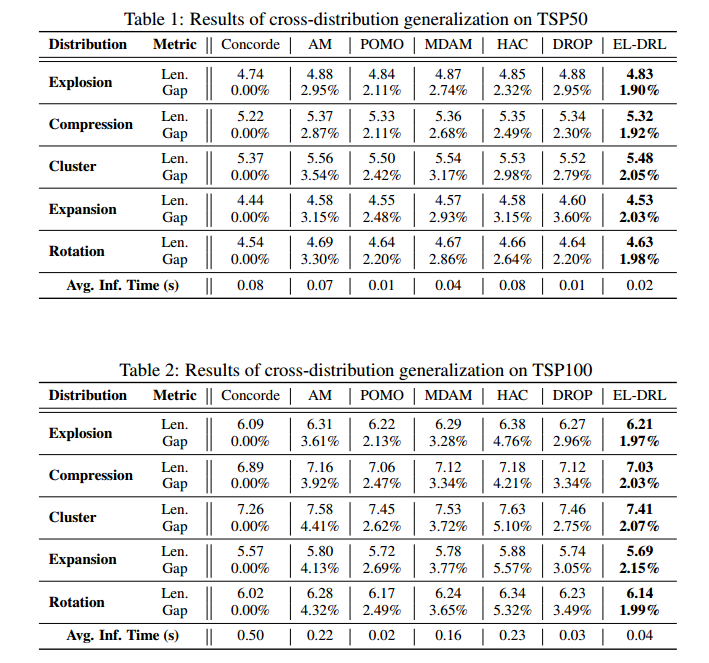
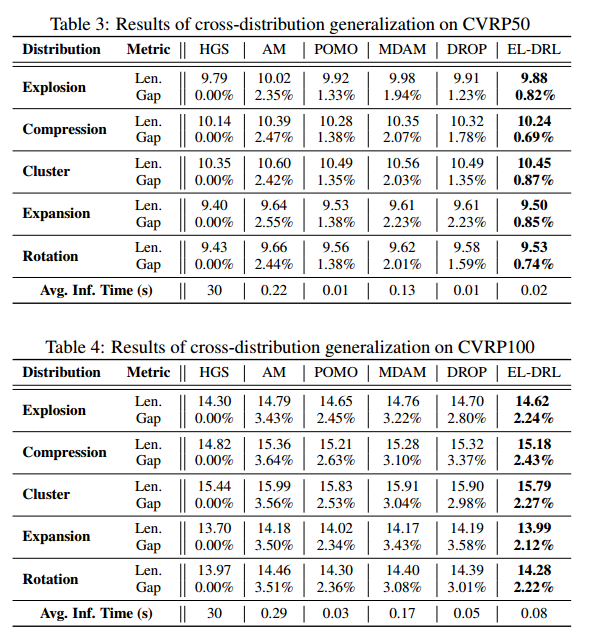
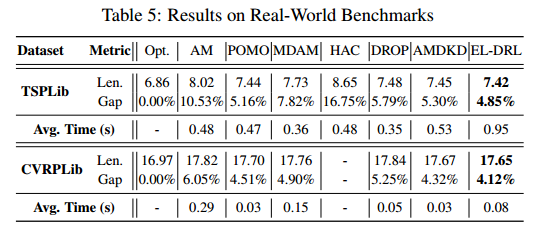
泛化性能比其他方法要好
消融实验
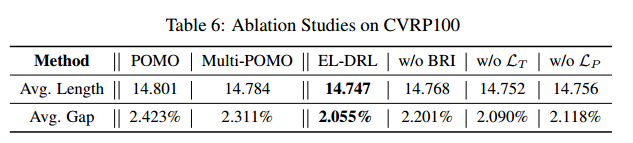
单个POMO、四个POMP(EL-DRL就是四个POMP)
EL-DRL、EL-DRL去除随机初始化、EL-DRL去除 $\mathcal{L}_T$、EL-DRL去除 $\mathcal{L}_P$
限制
处理大规模问题不太行,主要是因为POMO处理大规模本身就不太行。
展望:
- 探索分支算法来解决大规模问题
- 引入稀疏性来提升计算的效率
- 增强可解释性,进一步加强子模型之间的协作
- 推广到非路径的组合优化