DeepACO Neural-enhanced Ant Systems for Combinatorial Optimization
DeepACO:用于组合优化的神经增强蚁群系统

代码:https://github.com/henry-yeh/DeepACO
摘要
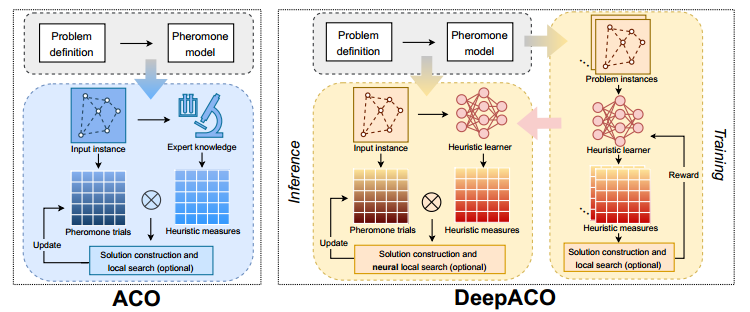
蚁群优化算法是一种元启发式算法,已成功地应用于各种组合优化问题。传统上,针对特定问题定制蚁群算法需要知识驱动的启发式专家设计。在本文中,我们提出了DeepACO,这是一个利用深度强化学习来自动化启发式设计的通用框架。DeepACO增强了现有蚁群算法的启发式度量,并在未来的蚁群算法应用中省去了繁琐的人工设计。作为一种神经增强型元启发式算法,DeepACO在使用单个神经模型和一组超参数的情况下,在8个cop上的表现始终优于同类的蚁群算法。作为一种神经组合优化方法,DeepACO在规范路由问题上的表现优于或等同于特定问题的方法。我们的代码可以在https://github.com/henry-yeh/DeepACO上公开获得。
介绍
自然界中的蚂蚁系统是自我学习的。它们利用化学信号和环境线索来定位并将食物送回蚁群。蚂蚁留下的信息素痕迹表明食物来源的质量和距离。信息素轨迹的强度随着蚂蚁数量的增加而增加,由于蒸发而减少,形成了一个自我学习的觅食系统。
蚁群算法部署一群人工蚂蚁,通过重复的解构建和信息素更新来探索解空间。通过特定实例的信息素跟踪和特定问题的启发式措施,探索偏向于更有前途的领域。信息素轨迹和启发式测量都表明解决方案成分的前景如何。通常,信息素轨迹对所有解决方案组件进行统一初始化,并在解决实例时学习。相反,启发式措施是基于对问题的先验知识预先定义的,为复杂的cop设计适当的启发式措施是相当具有挑战性的。
挑战:
- 需要额外的努力,使蚁群算法的灵活性降低;
- 启发式测度的有效性严重依赖于专家知识和人工调优;
- 考虑到缺乏可用的专家知识,为研究较少的问题设计启发式测量可能特别具有挑战性。
本文提出了一种通用的神经增强型蚁群算法DeepACO,并解决了上述局限性。DeepACO增强了现有蚁群算法的启发式度量,并在未来的蚁群算法应用中省去了繁琐的人工设计。它主要包括两个学习阶段。
- 第一阶段通过跨COP实例训练神经模型来学习从实例到启发式度量的特定问题映射。
- 第二阶段在学习测度的指导下,学习实例特定信息素轨迹,同时用蚁群算法求解实例。在第一阶段学习到的启发式度量通过偏向解结构和引导局部搜索(LS)逃避局部最优而被纳入蚁群算法(第二学习阶段)。
DeepACO提供了覆盖路由、分配、调度和子集问题的八种cop的有效神经增强,是我们所知评估最广泛的NCO技术。
作为人工智能算法的神经增强版,DeepACO在使用单个神经模型和一组超参数的情况下,只需要几分钟的训练,就能在8个cop上持续优于同类算法。作为一种NCO方法,在规范路由问题上,DeepACO比最先进的(SOTA)和特定问题的NCO方法表现得更好或更具竞争力,同时更易于推广到其他cop。据我们所知,我们是第一个利用深度强化学习(DRL)来指导蚁群算法元启发式进化的人。
贡献:
- 提出DeepACO,一个神经增强的蚁群算法元启发式算法。它加强了现有的蚁群算法,并在未来的蚁群算法应用中省去了费力的人工设计。
- 提出了三种扩展的DeepACO实现来平衡探索和开发,这通常可以应用于基于热图的NCO方法。
- 验证了DeepACO在八个cop中始终优于其ACO同行,同时表现优于或等同于特定问题的NCO方法。
相关工作
- NCO,神经组合优化
- 分为端到端和混合方法,DeepACO属于后者
- 端到端方法学习自回归解的构造或者热图生成,以便后续基于采样的解码,方法包括:better-aligned神经架构、改进的训练范例、advanced solution pipelines、broader applications。构造后可以通过迭代和其他算法进一步改进。
- 混合算法包含神经学习在启发式中做出决策或者生成热图来辅助启发式:要么让神经网络在算法循环中做出决策,要么一次性生成热图用于辅助后续算法。
- 学习边缘分数和节点惩罚来指导LKH-3的搜索过程:Combining deep learning model with linkernighan-helsgaun heuristic for solving the traveling salesman problem.
- 训练神经模型来预测路由问题中的有希望的边,为动态规划提供了神经促进:Deep policy dynamic programming for vehicle routing problems.
- 训练小规模GNN为大型TSP实例构建热图,并将热图馈送到蒙特卡罗树搜索中以改进解决方案:Generalize a small pre-trained model to arbitrarily large tsp instances
- 利用神经模型在导引局部搜索TSP中产生regret:Graph neural network guided local search for the traveling salesperson problem.
- 蚁群算法
- ML-ACO:Boosting ant colony optimization via solution prediction and machine learning.
蚁群算法的预备知识
COP模型
COP模型包括:
- 搜索空间 $S$ 定义了一组离散决策变量 $X_i,i=1,\cdots,n$,其中每个决策变量 $X_i$ 取自一个有限集合 $D_i=\lbrace v_i^1,\cdots,v_i^{\mid D_i\mid}\rbrace$
- 决策变量必须满足的一组约束 $\Omega$
- 目标函数 $f\rightarrow \mathbb{R}_0^+$ 求最小值
COP的一个可行解 $s$ 是所有满足 $\Omega$ 的决策变量的完整assignment
信息素模型
(有点抽象,没看懂)
COP模型定义了蚁群算法的信息素模型。不是一般性,信息素模型是一个以决策变量为节点,以解分量为边的构造图。每个解分量 $c_{ij}$,表示值 $v_i^j$ 对决策变量 $X_i$ 的分配,与他的信息素尝试 $\tau_{ij}$ 和启发式测度 $\eta_{ij}$ 相关联。$\tau_{ij}$ 和 $\eta_{ij}$ 都与解中包含 $c_{ij}$ 的可能性相关。通常,蚁群算法会统一初始化和迭代更新信息素,预先定义和修正启发式测度。
举个例子,在TSP中,$c_{ij}$ 表示解中是否包含 $i$ 到 $j$ 这条边,$\tau_{ij}$ 可以表示成 $i$ 到 $j$ 的距离的倒数。
构造解和局部搜索(可选)
在 $\tau_{ij}$ 和 $\eta_{ij}$ 的偏置下, 人工蚂蚁通过遍历构造图可以构造出一个解 $s=\lbrace s_t\rbrace_{t=1}^n$。如果 $t$ 时刻蚂蚁在节点 $i$,此时已经有一个局部解 $s_{<t}=\lbrace s_t\rbrace_{t=1}^{t-1}$,蚂蚁选择 $j$ 作为下一个目的地的概率可以表示成
\[\left.P(s_t|s_{<t},\rho)=\left\lbrace \begin{array}{ll} \frac{\tau_{ij}^\alpha\cdot\eta_{ij}^\beta}{\sum_{c_{il}\in\boldsymbol{N}(s_{<t})}\tau_{il}^\alpha\cdot\eta_{il}^\beta} &\text{if}\quad c_{ij}\in\boldsymbol{N}(s_{<t}),\\ 0 &\text{otherwise.} \end{array} \right.\right.\]其中,$\rho$ 是一个实例,$N(s_{<t})$ 是局部可行解的集合,$\alpha,\beta$ 是控制参数,一般都设置为1。
生成完整解的概率模型为
\[P(s|\boldsymbol{\rho})=\prod_{t=1}^{n}P(s_{t}|\boldsymbol{s}_{<t},\boldsymbol{\rho}).\]构造解后,可以用局部搜索来优化。
信息素更新
解构建完成后,信息素更新过程对解进行评价,并对信息素轨迹进行相应调整,即优质解中各组分的信息素轨迹增加,劣质解中各组分的信息素轨迹减少。具体的更新规则可能因所使用的ACO变体而异。
方法
参数化启发式空间
引入了一个启发式学习器,是一个具有可训练参数 $\theta$ 的GNN。这个启发式学习器会将一个输入的COP实例 $\rho$ 映射到一个启发式测度 $\eta_\theta(\rho)$。他包含了与每个解分量 $c_{ij}$ 相关的非负实数 $\eta_{ij;\theta}$。该部分的偏置项计算为,
\[P_{\eta_\theta}(s|\boldsymbol{\rho})=\prod_{t=1}^{n}P_{\eta_\theta}(s_{t}|\boldsymbol{s}_{<t},\boldsymbol{\rho}).\]Local search interleaved with neural-guided perturbation
一方面,局部搜索是短视的,很容易陷入局部最优。
另一方面,由于COP很复杂,仅学习启发式测度是不够的,因此可以选择应用局部搜索来优化构造的解。
因此提出了NLS,不知道怎么翻译了。
基于这些考虑,我们在算法1中提出了LS与神经引导摄动(简称NLS)交织。NLS以较低的目标值为目标,与神经引导的扰动相交叉,使学习到的最优值偏置。在每次迭代中,第一阶段利用LS重复改进解决方案,直到(潜在地)达到局部最优。第二阶段利用LS稍微扰动局部最优解,以获得更高的累积启发式度量。
Based on these considerations, we propose LS interleaved with neural-guided perturbation (NLS for short) in Algorithm 1. NLS interleaves LS aiming for a lower objective value and neural-guided perturbation biasing the learned optima. In each iteration, the first stage utilizes LS to repeatedly refine a solution until (potentially) reaching local optima. The second stage utilizes LS to slightly perturb the locally optimal solution toward gaining higher cumulative heuristic measures.
算法的流程

(我不是很懂这个第六行具体怎么计算,从TSP角度来看 $\frac{1}{\eta_{ij;\theta}}=dis_{ij}$,越小越好)
启发式训练学习器
启发式学习器 $\theta$ 将实例 $\rho$ 映射到他的启发式度量 $\eta_\theta$。将构造解和NLS精化构造接的期望目标值都最小化
\[\mathrm{minimize}\quad\mathcal{L}(\boldsymbol{\theta}|\boldsymbol{\rho})=\mathbb{E}_{\boldsymbol{s}\sim P_{\boldsymbol{\eta}_{\theta}}(\cdot|\boldsymbol{\rho})}[f(\boldsymbol{s})+Wf(NLS(\boldsymbol{s},f,+\infty))],\]其中 $W$ 是平衡两个部分的一个系数。目标函数的第一个部分鼓励直接构造最优解,但是往往很难学习;第二个部分鼓励构造适合NLS去搜索的解,但由于第二个部分的方差很小,直接使用第二部分会导致训练效率很低。NLS本身不涉及梯度。
按照上式构建蚁群系统,信息素固定为1以确保无偏估计。Reinforcement的梯度为
\[\nabla\mathcal{L}(\theta|\rho)=\mathbb{E}_{\boldsymbol{s}\sim P_{\boldsymbol{\theta}}(\cdot|\rho)}[((f(\boldsymbol{s})-b(\boldsymbol{\rho}))+W(f(NLS(\boldsymbol{s},f,+\infty))-b_{NLS}(\boldsymbol{\rho})))\nabla_{\boldsymbol{\theta}}\log P_{\boldsymbol{\eta}\boldsymbol{\theta}}(\boldsymbol{s}|\boldsymbol{\rho})]\]其中 $b(\rho)$ 和 $b_{NLS}(\rho)$ 是构造解和NLS精化解的平均目标函数值。
我个人的一点想法:
\[\mathrm{minimize}\quad\mathcal{L}(\boldsymbol{\theta}|\boldsymbol{\rho})=\mathbb{E}_{\boldsymbol{s}\sim P_{\boldsymbol{\eta}_{\theta}}(\cdot|\boldsymbol{\rho})}[f(\boldsymbol{s})],\]如果目标函数变成这样,就是没有NLS的部分,这不就是普通的构造法吗,那个启发式测度,就是一个概率向量吧?
感觉好像只是引入了一个蚁群的概念
更好的探索
进一步提出三种扩展设计
多头解码器
Multihad DeepACO在GNN上实现了 $m$ 个解码器,旨在生成不同的启发式措施。
$m$ 个解码器单独计算损失,并加入额外的KL散度
\[\mathcal{L}_{KL}(\boldsymbol{\theta}|\boldsymbol{\rho})=-\frac{1}{m^{2}n}\sum_{k=1}^{m}\sum_{l=1}^{m}\sum_{i=1}^{n}\sum_{j=1}^{|\boldsymbol{D}_{i}|}\tilde{\boldsymbol{n}}_{ij;\boldsymbol{\theta}}^{k}\log\frac{\tilde{\boldsymbol{\eta}}_{ij;\boldsymbol{\theta}}^{k}}{\tilde{\boldsymbol{\eta}}_{ij;\boldsymbol{\theta}}^{l}},\]其中,上头加波浪线表示归一化。
在推理阶段,Multihead DeepACO在各自的MLP解码器引导下部署m个蚁群,而整个蚁群共享同一组信息素轨迹。
KL散度,Kullback-Leibler divergence,用来衡量两个模型之间的差距
KL散度源于信息论,先给出熵的定义
\[H=-\sum_{i=1}^Np(x_i)\log p(x_i)\]其中,$p(x_i)$ 表示 $x_i$ 出现的概率,也就是说 $p$ 是一个概率分布。
现在要比较两个概率分布 $p,q$。KL散度即为
\[D_{KL}(p\mid\mid q)=\sum_{i=1}^Np(x_i)(\log p(x_i)-\log q(x_i))\]本质上,KL散度是两个概率分布模型之间对数差的期望,可以表示成
\[D_{KL}(p\mid\mid q)=E[\log p(x_i)-\log q(x_i)]\]在平时使用中,KL散度一般写成
\[D_{KL}(p\mid\mid q)=\sum_{i=1}^Np(x_i)\log\frac{p(x_i)}{q(x_i)}\]KL散度越小,表示差异越小。
值得注意的是,KL散度不是距离,是非对称的。比较 $D_{KL}(p\mid\mid q)$ 和 $D_{KL}(r\mid\mid q)$ 可以衡量 $p,r$ 哪个更接近 $q$,但是比较 $D_{KL}(p\mid\mid q),D_{KL}(r\mid\mid q),D_{KL}(p\mid\mid r)$ 三个之间的数值关系是没有意义的。
Top-k 熵损失
熵损失激励agent保持其行为的多样性。它通常用作正则化器,以鼓励探索并防止过早收敛到次优策略。然而,在COP上下文中,大多数解决方案组件远不是下一步解决方案构建的合理选择。鉴于此,在上面目标函数损失是应用了Top-k 伤损失,形式为
\[\mathcal{L}_H(\boldsymbol{\theta}|\boldsymbol{\rho})=\frac{1}{n}\sum_{i=1}^n\sum_{j\in\mathcal{K}_i}\bar{\boldsymbol{\eta}}_{ij;\boldsymbol{\theta}}\log(\bar{\boldsymbol{\eta}}_{ij;\boldsymbol{\theta}}).\]其中,$\mathcal{K}i$ 是包含决策变量 $X_i$ 的top k个解分量的集合。$\bar{\boldsymbol{\eta}}{ij;\boldsymbol{\theta}}$ 表示归一化。
模仿损失
如果有专家设计的启发式测度,可以加入额外的模仿损失,使启发式学习器学习专家损失。优点
- 作为正则化维持探索
- 学习专家知识
$\tilde{\boldsymbol{\eta}}_{ij}^\ast$ 表示归一化的专家设计的启发式测度。
实验
实验设置
我们在8个典型的cop问题上对DeepACO进行了评估,包括旅行商问题(TSP)、有能力车辆路线问题(CVRP)、定向问题(OP)、计奖旅行商问题(PCTSP)、顺序排序问题(SOP)、单机总加权延迟问题(SMTWTP)、资源约束项目调度问题(RCPSP)和多背包问题(MKP)。它们涵盖了路由、分配、调度和子集COP类型。
DeepACO作为增强的ACO算法
在这一部分中,我们不使用NLS,并将W设为0进行训练。它只需要几分钟的训练就可以提供大量的神经增强。另一方面,对于DeepACO来说,额外的推理时间可以忽略不计。例如,TSP100的响应时间小于0.001秒。
基本蚁群算法的DeepACO
我们基于三个基本的蚁群算法元启发式实现DeepACO:蚂蚁系统、Elitist蚂蚁系统和MAX-MIN蚂蚁系统(三个SOTA蚂蚁系统)。实验结果验证了DeepACO可以带来的通用神经增强。
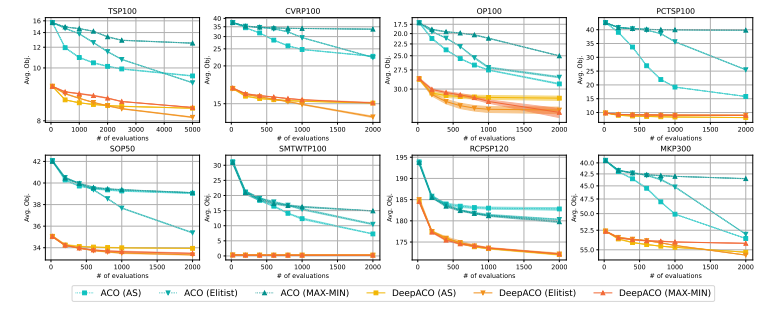
(附件中有更详细的数据比较和具体的定义)
DeepACO for advanced ACO algorithms
将DeepACO应用于自适应精英蚂蚁系统(AEAS),这是一种具有特定问题适应性的新型蚁群算法。实验结果标明,DeepACO表现出明显更好的性能。鉴于此,作者认为利用DeepACO设计新的ACO SOTAs是有希望的。
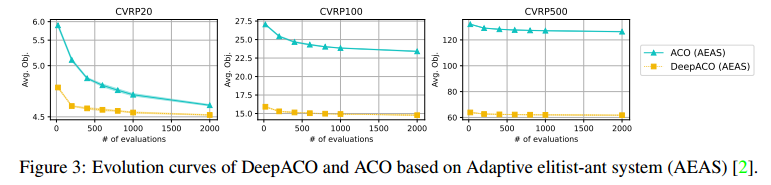
不同信息素模型的DeepACO
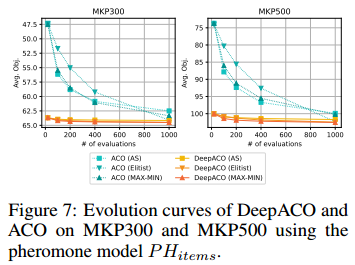
蚁群算法可以有不同的信息素模型。比如单个节点的信息素模型和连续多个节点的信息素模型。文章指出,只需要加一个MLP就可以把单个节点的信息素拓展到连续多个节点的信息素模型。
在多重背包问题MKP上探究,只用单个节点的信息素模型已经优于ACO。
验证了DeeoACO能够很容易拓展不同的信息素模型。
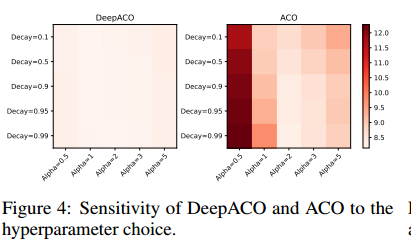
对超参数选择有更好的鲁棒性
两个重要的超参数,控制解构造转移概率的 Alpha 和控制信息素更新的 Decay。在TSP100上评估,颜色越浅表示方差越小,表明了DeepACO对超参数有更强的鲁棒性。作者认为数据驱动的训练可以省去高要求的超参数调优专家知识。
DeepACO as an NCO method
在路由问题上
$W$ 设置为9。
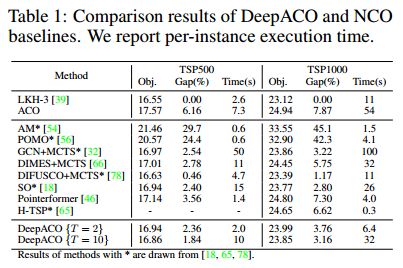
上述的方法大多针对TSP设计的,而DeepACO是一个通用的元启发式方法,虽有差距,但已经很有竞争力了。
消融实验:(1)只用LS并用更多迭代;(2)用随机扰动不用那个 $\eta$ 扰动;(3)$W=0$
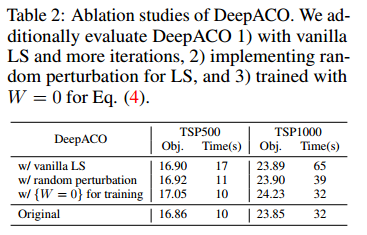
对热图更好地探索
加入上述所说的三个扩展设计,解码器用4个头,top-K设置为4.
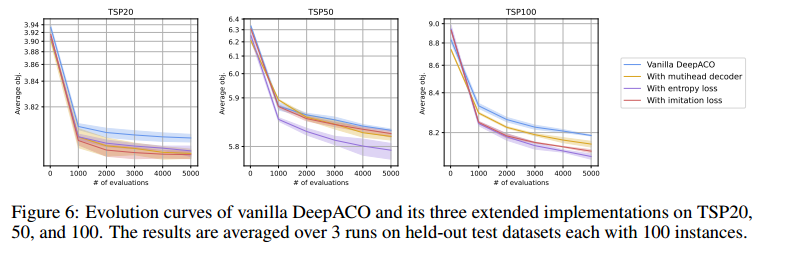
在小规模的TSP20、50、100上表现更好,因为小规模的COP通常需要更多地探索。
增强热图解码与信息素更新
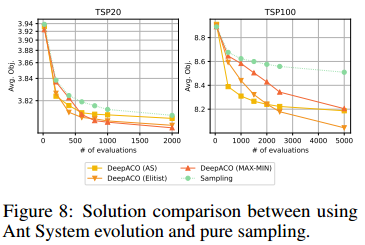
展示了用信息素自学习比直接纯采样要优秀。
总结
限制:
-
将所有学习到的启发式信息压缩到启发式度量的n × n矩阵中,DeepACO可能受到限制。
-
不包含局部搜索组件时效果不好。
未来:研究3D或者动态启发式。