论文阅读 组合优化 NIPS

Learning to Search Feasible and Infeasible Regions of Routing Problems with Flexible Neural k-Opt

NIPS23 k-opt learn to imporve + mask优化不可行探索 + 双流解码器

Posted by Birdie on January 21, 2024

Learning to Search Feasible and Infeasible Regions of Routing Problems with Flexible Neural k-Opt

用柔性神经k-Opt学习搜索路由问题的可行和不可行区域

image-20240120180037015

开源：https://github.com/yining043/NeuOpt

摘要

在本文中，我们提出了神经k-Opt (NeuOpt)，一个新的路由问题的学习搜索(L2S)求解器。它学习基于定制的动作分解方法和定制的循环双流解码器来执行灵活的k-opt交换。作为规避纯可行性掩蔽方案，实现可行和不可行区域自主探索的开创性工作，我们随后提出了导引不可行区域探索(Guided infeasible Region exploration, ire)方案，该方案为NeuOpt策略网络补充了与可行性相关的特征，并利用奖励塑造更有效地引导强化学习。此外，我们为NeuOpt配备了动态数据增强(D2A)，以便在推理过程中进行更多样化的搜索。在旅行商问题(TSP)和有能力车辆路线问题(CVRP)上的大量实验表明，我们的NeuOpt不仅显著优于现有的(基于掩码的)L2S求解器，而且比学习构造(L2C)和学习预测(L2P)求解器显示出优越性。值得注意的是，我们提供了关于神经解算器如何处理VRP约束的新视角。我们的代码是可用的:https://github.com/yining043/NeuOpt。

介绍

learning-to-construct (L2C), learning-tosearch (L2S), and learning-to-predict (L2P)

  • L2C，快，但难以逃脱局部最优解
  • L2P，擅长预测关键信息，如边缘热图，但对于大规模实例缺乏通用性，无法处理TSP以外的VRP约束
  • L2S，慢

目前的L2S大多利用较小的k-opt（k=2,3），部分原因是难以有效处理较大的k。

为了解决这个问题，作者引入了Neural k-opt (NeuOpt)，能够处理任何k≥2的k-opt。具体来说，它采用了一种定制的动作分解方法，将复杂的k-opt交换简化并分解为一系列基本动作(S-move, I-move和E-move)，其中I-move的数量决定了具体执行的k-opt动作的k。这样的设计使得kopt交换可以很容易地逐步构建，更重要的是，它为深度模型提供了显式和自动确定适当k的灵活性。这进一步使得不同的k值可以在不同的搜索步骤中组合，在粗粒度(较大k)和细粒度(较小k)搜索之间取得平衡。相应地，作者设计了一个循环双流(RDS)解码器来解码这种动作分解，该解码器由循环网络和两个互补的解码流组成，用于上下文建模和注意力计算，从而捕获移除边缘和添加边缘之间的强相关性和依赖性。

现在的L2S用mask将搜索空间限制在可行区域，作者引入了一种新的引导不可行区域探索（GIRE）的方案。GIRE有四个优势：

  • 避免了对ground-truth动作掩模的非简单计算
  • 促进了在更有希望的可行性边界上的搜索
  • 它连接(可能是孤立的)可行区域，帮助摆脱局部最优并发现通往更好解决方案的捷径
  • 它强制明确意识到VRP约束

文献回顾

  • L2C：RNN、GNN、AM、POMO、EAS、SGBS
  • L2S：NeuRewriter、NLNS、guide 2-opt、DAC-Att，长时间搜索效果仍然不如POMO和EAS
  • L2P：GNN+beam search、GLS、DIFUSCO
  • 可行性满足：mask，传统求解器中可能会违反约束有一定的好处

预备知识和记号

  • vrp记号

  • 传统的k-opt启发式

    • 调整原解中的k条边变成新的k条边

    • LK算法（LKH采用的算法）通过几个标准缩小搜索范围，作者采用了其中一个原则，叫做顺序交换原则

    • 定义顺序交换标准：对于 $i=1,\cdots,k$， 被移除的边 $e_i^{\text{out}}$ 和新加入的边 $e_i^{\text{in}}$ 共享一个端点，$e_i^{\text{in}}$ 和 $e_{i+1}^{\text{out}}$ 也必须是。

    • Moreover, the LK algorithm considers scheduling varying k values in a repeated ascending order, so as to escape local optima by varying search neighbourhoods.

      此外，LK算法考虑以重复升序调度变化的k值，从而通过改变搜索邻域来逃避局部最优。

      这是作者采用的第二个原则，本文的算法也是基于LK的这两个原则，这个没看懂

    • Helsgaun在开源的LKH求解器中实现了LK算法，增加了非顺序交换和边缘候选集。然后升级为LKH-2，利用更一般的k-opt交换、分而治之策略等。最新版本LKH-3通过惩罚违反约束的行为，进一步解决了受约束的vrp，使其成为一种通用且强大的求解器，可作为神经方法的基准。

    • 目前最先进的混合遗传搜索求解器HGS也是用的k-opt

Neural k-opt(NeuOpt)

三个挑战：

  • 对于任意 $k\geq 2$，求解器应该是通用的，使用统一的公式和框架
  • 在考虑移除边和添加边之间的强相关性和依赖性的同时，对复杂动作空间进行连贯的参数化
  • 它应该动态调整k，以平衡粗粒度(较大k)和细粒度(较小k)的搜索步骤

公式化

引入一种新的分解方法，使用三个基本移动的组合来构建k-opt：starting move、intermediate move、ending move，缩写成：S-move、I-move、E-move，其中k对应了确定 I-move 的数量。

S-move

第一步是要移除一条边 $e^{\text{out}}(x_a\rightarrow x_b)$，使得TSP的解从一个环变成一条两个端点为 $x_a,x_b$ 的链。S-move只在动作开始的时候执行，可以表示成 $S(x_a)$。因为如果 $x_a$ 被指定，那么 $x_b$ 是唯一确定的。称源节点 $x_a$ 叫做anchor node，来计算 node rank。

node rank定义为，在原本的TSP环中，$x_u(x_u\in\mathcal{V})$ 到 $x_a$ 最少经过的边数，表示为 $\Gamma(a,u)$。

I-move

假设 $x_i,x_j$ 是当前这条TSP链的两个端点。为了避免连续的 I-move 之间的冲突，定义了新加入的边 $e^{\text{in}}(x_u\rightarrow x_v)$ 之间的顺序条件

  • $x_u$ 必须要有更低的 node rank，比如 $x_u=x_i$
  • $x_v$ 的 node rank 必须大于 $x_i,x_j$，即 $\Gamma(a,i)<\Gamma(a,j)<\Gamma(a,v)$

步骤

  1. 移除 $e^{\text{out}}(x_v\rightarrow x_w)$
  2. 翻转 $x_v$ 和 $x_j$ 之间所有边的方向
  3. 加入 $e^{\text{in}}(x_u,x_v)$

给定 $x_v$ 可以确定当前 I-move 的全部操作，记作 $I(x_v)$

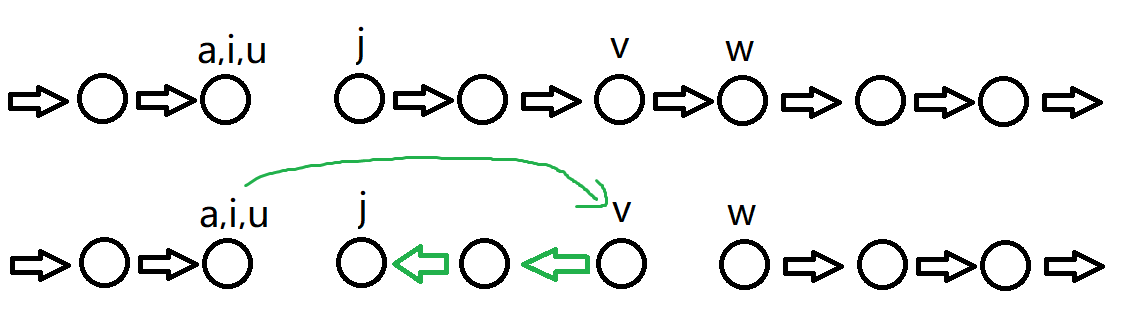
image-20240121204643236

E-move

最后只需要将这条链变成环即可。

如果 I-move 的条件2松动成 $\Gamma(a,j)\leq \Gamma(a,v)$，那么 E-move 可以变成一个 general I-move，记作 $I’(x_j)$ 或者 $E(x_j)$。

MDP

  • state：$s_t=\lbrace\mathcal{G},\tau_t,\tau_t^{\text{bsf}}\rbrace$，表示实例、当前时刻解、到当前时刻为止的最优解
  • action：$a_t=\lbrace\Phi_k(x_k),k=1,\cdots,K\rbrace$，其中 $\Phi_1$ 是 S-move，后面的全是 I-move，最后一个可能是 general I-move，E-move视作转移的时候自动添加
  • reward：$r_t=f(\tau_t^{\text{bsf}})-\min[f(\tau_{t+1}),f(\tau_t^{\text{bsf}})]$

值得注意的是，为了保证action一定长度是 K，动作可以是空

Recurrent Dual-Stream（RDS）decoder

NeuOpt是encoder-decoder结构的策略网络。

编码器和N2S是一样的，只是NFEs的全连接层变成了一个MLP。

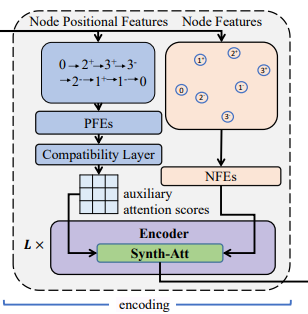
image-20240121211534308

动作分解的GRUs

\[\pi_{\theta}(a\mid s)=P_{\theta}(\Phi_{1}(x_{1}),\Phi_{2}(x_{2}),\ldots,\Phi_{K}(x_{K})\mid s)=\prod_{\kappa=1}^{K}P_{\theta}^{\kappa}(\Phi_{\kappa}\mid \Phi_{1},..,\Phi_{\kappa-1},s)\]

$P_\theta^{k}$ 是一个用GRU（比LSTM更简单的门控循环单元）实现的概率分布模型，输入的编码器的嵌入 $h_i$ 和历史动作 $\lbrace\Phi_1,\cdots,\Phi_{\kappa-1}\rbrace$

原本的GRU的隐藏层状态 $q^\kappa$ 是从 $q^{\kappa-1}$ 继承过来，并用输入 $o^\kappa$ 作为偏置。但现在为了考虑容纳更多的上下文信息，引入了两个流 $\mu,\lambda$。

\[q_\mu^\kappa=\text{GRU}\left(o_\mu^\kappa,q_\mu^{\kappa-1}\right),q_\lambda^\kappa=\text{GRU}\left(o_\lambda^\kappa,q_\lambda^{\kappa-1}\right)\]

其中，$q_\mu^0=q_\lambda^0=\frac{1}{N}\sum_{i=1}^Nh_i$

对偶流上下文模型

$\mu$ 是 move 流，$\lambda$ 是 edge 流。

简单来说，$\mu$ 的输入是上一个动作的节点，即 $o_\mu^\kappa=h_{\kappa}$，即上一个 $\Phi_{\kappa-1}(x_{\kappa-1})$ 的信息。

$\lambda$ 的信息是边的信息，即 $o_{\lambda}^\kappa=h_{i_\kappa}$，即当前解的源节点。

计算方面也是采用注意力机制：

\[\begin{aligned}\mu_{\kappa}&=\text{Tanh}\left((q_{\mu}^{\kappa}W_{\mu}^{\text{Query}} + h W _ { \mu }^{\textbf{Key}} ) + ( q _ { \mu }^{\kappa}W_{\mu}^{\text{Query}^{\prime}})\odot(hW_{\mu}^{\text{Key}^{\prime}})\right)W_{\mu}^{O},\\\lambda_{\kappa}&=\text{Tanh}\left((q_{\lambda}^{\kappa}W_{\lambda}^{\text{Query}} + h W _ { \lambda }^{\textbf{Key}} ) + ( q _ { \lambda }^{\kappa}W_{\lambda}^{\text{Query}^{\prime}})\odot(hW_{\lambda}^{\text{Key}^{\prime}})\right)W_{\lambda}^{O},\end{aligned}\]

推理时候的动态数据增强

连续若干轮都没有找到更好的解的时候，即陷入局部最优，就进行数据增强。

引导不可行区域探索（GIRE）

可行区域通常是碎片化的孤岛。神经解算器中的掩蔽通常将搜索限制在可行区域，这可能导致搜索轨迹效率低下或无法找到全局最优解。

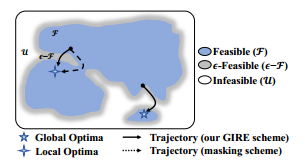
image-20240121214728905

CVRP的搜索空间

$\mathcal{F}$ 是满足TSP且满足容量约束的解的集合；

$\mathcal{U}$ 是满足TSP但不满足容量约束的解的集合；

$\epsilon-\mathcal{F}\subseteq\mathcal{U}$ 是容量违规百分比不超过 $\lambda$ 的解集。

功能补充

GIRE在策略网络中补充了 违反指标（Violation Indicator，VI）和勘探统计（Exploration Statistics，ES），已识别特定的约束违规行为并了解正在进行的探索行为。

VI 记录了当前解决方案中特定的不可行的部分，对于CVRP，使用两个二元变量分别表示访问特定节点之前或之后的累计容量是否超过容量限制。

ES 提供了正在探索行为的统计数据，定义

\[\mathcal{H}_t:=\left\{\left(\tau_{t^{\prime}} \rightarrow \tau_{t^{\prime}+1}\right)\right\}\mid_{t^{\prime}=t-T_{\text {his }}} ^{t-1}\]

作为最近 $T_{\text{his}}$ 步转换的集合。ES特征 $\mathcal{J}_t$ 由 $\mathcal{H}_t$ 导出的估计可行性转移概率组成，包括

\[P\left(\tau \in \mathcal{U}, \tau^{\prime} \in \mathcal{U}\right), P\left(\tau^{\prime} \in \mathcal{F} \mid \tau \in \mathcal{U}\right), P\left(\tau^{\prime} \in \mathcal{U} \mid \tau \in \mathcal{F}\right), P\left(\tau^{\prime} \in \mathcal{F} \mid \tau \in \mathcal{F}\right)\]

，以及一个二元指标表示当前解的可行性。为了使策略网络依赖这些ES特征，引入了两个超网络 $\text{MLP}_{\mu}$ 和 $\text{MLP}_{\lambda}$，以 $\mathcal{J}_{t}$ 为输入，生成上述对偶流上下文模型中的 $W_{\mu}^O, W_{\lambda^O}$。网络结构是（9 x 8 x d）以减少计算成本。

奖励塑造

奖励表示为

\[r_t^{\mathrm{GIRE}}=r_t+\alpha \cdot r_t^{\mathrm{reg}}+\beta \cdot r_t^{\text {bonus }}\]

$r_t$ 是原始奖励，$r_t^{\text {reg }}$ 负责调解计算探索行为，$r_t^{\text {bonus }}$ 鼓励在 $\epsilon-\mathcal{F}$ 探索，$\alpha,\beta=0.05$。

\[\begin{gathered} r_t^{\mathrm{reg}}=-\mathbb{E}\left[r_t\right] \times\left[\mathbb{H}\left[P_t(\mathcal{U} \mid \mathcal{U}]\right)+\mathbb{H}\left[P_t(\mathcal{F} \mid \mathcal{F})\right]\right] \\ \mathbb{H}[P]=\operatorname{Clip}\left\{1-c_1 \log _2\left[c_2 \pi e P(1-P)\right], 0,1\right\}, c_1=0.5, c_2=2.5, \end{gathered}\]

其中， $P_t(\mathcal{U} \mid \mathcal{U})=$ $P\left(\tau^{\prime} \in \mathcal{U} \mid \tau \in \mathcal{U}\right)$ and $P_t(\mathcal{F} \mid \mathcal{F})=P\left(\tau^{\prime} \in \mathcal{F} \mid \tau \in \mathcal{F}\right)$ :

这是一个熵测度概率，熵测度 $\mathbb{H}[P]$ 在 P 过高或者过低的时候施加更大的惩罚。

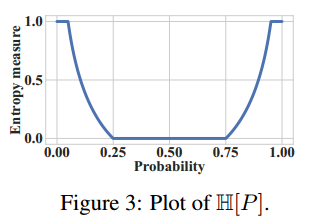
image-20240121220701845

$r_t^{\text {bonus }}$ 和 $r_t$ 的计算方法一样，只是定义域不同。

实验

对比实验

k=4

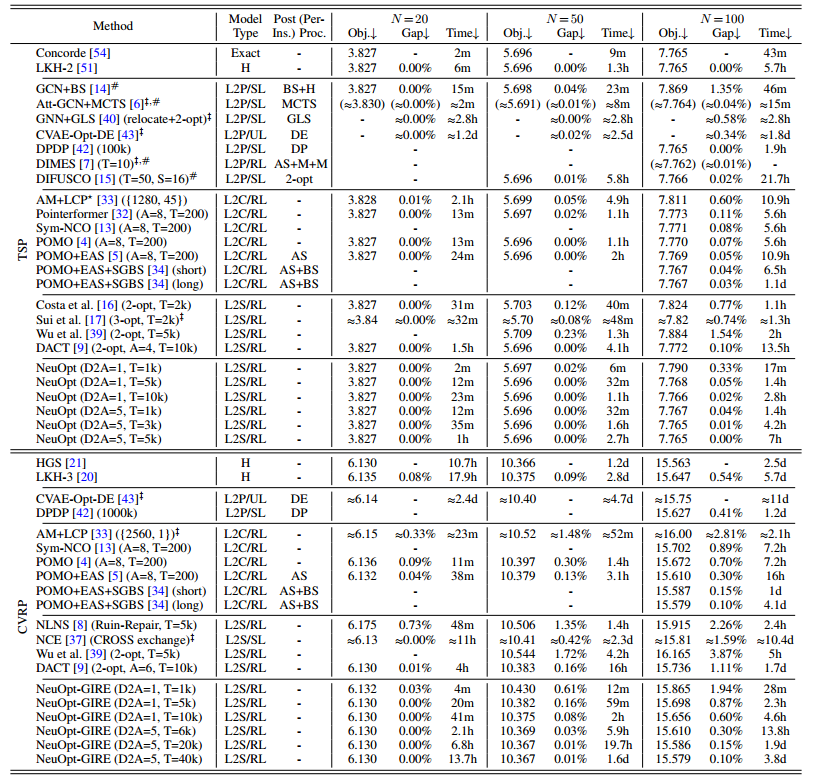
image-20240121220814472

POMP+EAS+SGBS是SOTA

TSP结果：

  • 跟L2P比：时间更快，解更准确，比最好的DIFUSCO要好
  • 跟L2C比，虽然小规模不如SOTA但比大多数要好，在TSP100上已经超过了SOTA。
  • 跟L2S比，时间快乐一倍

CVRP结果：

  • L2P做不了CVRP
  • 比L2C（SOTA）更快更好
  • 比L2S快

第一个在CVRP上超过LKH3的L2S求解器。

还与同样结构的DACT进行了比较

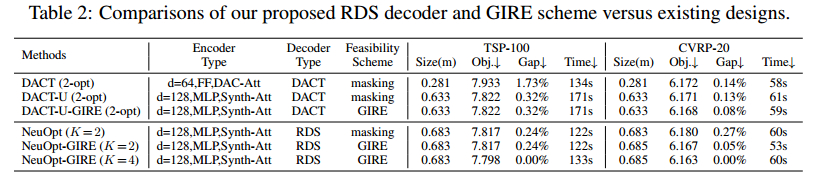
image-20240122140343444

消融实验

消 RDS decoder

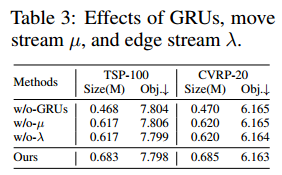
image-20240122140445029

有用，但感觉用处不大

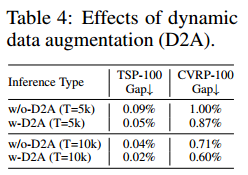
消 D2A 推理

image-20240122140656675

消 GIRE

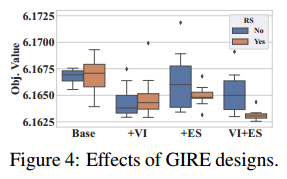
image-20240122140850163

在CVRP-20上对NeuOpt进行培训期间，我们考察了包括或排除违规指标(VI)、探索统计(ES)和奖励塑造(RS)的情景，并使用了它们的八种组合。我们在图4中为每个场景绘制了8次训练中获得的最佳目标值的箱形图。

我们可以得出结论:1)无论RS是否存在，补充VI都能持续提高训练效果;2)只有当RS存在时，ES的补充才会带来改善;3)我们完整的ire设计(VI+ES+RS)产生最低的客观值，并表现出卓越的稳定性。

消 basis moves

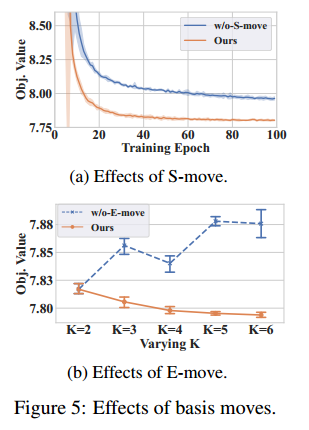
image-20240122141033727

上图，移除学习 S-move 采用随机选择，下图，只执行固定的 E-move

上图标明了 S-move 还是需要学习的，下图反应了 K 自适应变化的好处。

泛化实验

在标准数据集TSPLib和CVRPLlib上评估泛化。

image-20240122141324497

AMDKD 是 POMO 通过知识蒸馏来提高泛化性。

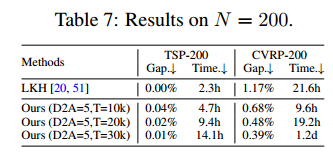
可扩展性：现有的L2S没法训练规模为200的CVRP，但ours可以直接找到最优解

image-20240122141524313

超参数学习

k

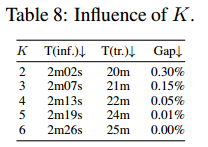
image-20240122141627949

k 越大，推理时间越久，但效果更好

GIRE 的参数

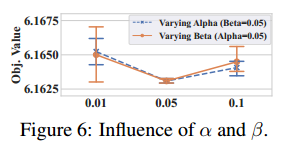
image-20240122141725501

总结和限制

大规模不如L2P，因此

  • 采用分治策略
  • 通过热图预测减少搜索空间
  • 采用可扩展的编码器
  • 用高度优化的CUDA重构代码

此外，还可以

  • 将 IRE 应用到更多 VRP 约束上
  • 集成 EAS
  • 增强不同大小、分布的泛化能力
CATALOG
    FEATURED TAGS
    神经网络 机器学习 机器人 webot 通信原理 并行计算 信息安全 自然语言处理 数据库 数字图像处理 软件工程 编译原理 强化学习 数字电路 proteus 计算机组成原理 VIVADO JAVA 论文阅读 组合优化 NIPS