Unsupervised Learning for Solving the Travelling Salesman Problem

求解旅行商问题的无监督学习

来自康奈尔大学

摘要

我们提出了一种用于解决旅行商问题(TSP)的无监督学习框架UTSP。我们使用代理损失来训练图神经网络(GNN)。GNN输出一个热图，表示每条边成为最优路径一部分的概率。然后，我们应用局部搜索来生成基于热图的最终预测。我们的损失函数由两部分组成:一部分推动模型寻找最短路径，另一部分作为路径应该形成哈密顿回路的约束的代理。实验结果表明，该方法优于现有的数据驱动的TSP启发式算法。我们的方法既具有参数效率，也具有数据效率:与强化学习或监督学习方法相比，该模型只需要约10%的参数数量和0.2%的训练样本。

介绍

精确算法：Concorde Applegate的割平面法，迭代求解TSP的线性规划松弛

启发式方法：LKH helsgan

POMO、元学习、SL+扩散模型、SL+热图+beam search

模型

作者以无监督学习(UL)的方式构建了一个数据驱动的TSP启发式算法，并以非自回归的方式生成热图。构造了一个包含两部分的代理损失函数：一部分鼓励GNN找到最短路径，另一部分作为约束的代理，即路径应该是所有节点上的哈密顿环。

代理丢失使我们能够更新模型，而不必解码完整的解决方案。这有助于缓解RL中遇到的稀疏奖励问题，从而避免不稳定的训练或缓慢的收敛。
UTSP方法不依赖于标记数据。这有助于模型避免在SL中遇到的昂贵的注释问题，并显著减少时间成本。UTSP模型，我们能够直接在更大的实例上训练我们的模型。

该模型将坐标作为GNN的输入。两个节点之间的距离决定了邻接矩阵中边的权值。训练完GNN后，使用局部搜索将热图转换为有效的路径。通过比较固定图大小高达1000个节点的TSP案例来评估UTSP的性能。注意到UTSP从根本上不同于RL，后者也可以被认为是无监督的。虽然强化学习需要马尔可夫决策过程(MDP)，并且在获得解后提取其奖励，但该方法不使用MDP，并且损失函数(奖励)是基于热图确定的。

总的来说，UTSP只需要少量(未标记的)数据，并通过使用无监督的代理损失函数和表达GNN来补偿它。使用UTSP构建的热图有助于减少搜索空间并生成“算法先验”，从而促进局部搜索。进一步表明，gnn的表达能力对于生成非光滑热图至关重要。

方法

GNN

通过距离矩阵 $D_{i,j}$ 构建邻接矩阵 $W_{i,j}=e^{-D_{i,j}/\tau}$ 以及节点特征（二维坐标） $F\in \mathbb{R}^{n\times 2}$，$\tau$ 是温度。

$F,W$ 传入GNN后生成软指标矩阵 $T\in\mathbb{R}^{n\times n}$。

模型使用散射注意力GNN（SAG），具有低通和带通滤波器，可以通过隐式学习节点加权来构建自适应表示，从而使用基于注意力架构的组合网络中的多个不同通道。最近的研究表明，SAG可以在保持轻量级的同时，为图组合问题（如最大团）输出表达性表示。

设 $S\in\mathbb{R}^{n\times n}$ 表示 SAG 的输出，首先对 $S$ 使用 softmax 激活函数，即 $T=softmax(S)$，接着使用 $T$ 构建热图 $\mathcal{H}\in\mathbb{R}^{n\times n}$。

构建热图

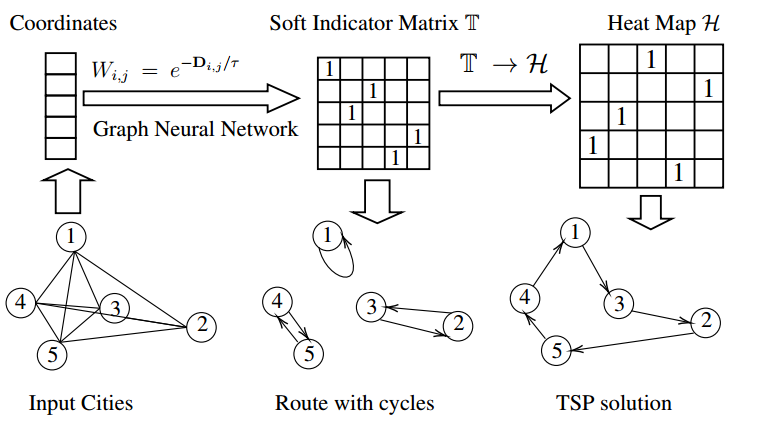
TSP的目标：哈密顿回路、最短路径

使用热图 $\mathcal{H}$ 为哈密顿回路约束设计替代损失具有挑战性，为此引入了 $T\rightarrow \mathcal{H}$ 变换，使其能够隐式地编码哈密顿回路约束。

直接使用 $T$ 会导致城市之间形成子环。

$T\rightarrow \mathcal{H}$ 变换

$\mathcal{H}_{i,j}$ 是边（i，j）是TSP最优解的概率，定义为

\[\mathcal{H}=\sum_{t=1}^{n-1}p_tp_{t+1}^T+p_np_1^T,\]

其中 $p_t\in\mathbb{R}^{n\times 1}$ 表示 $T$ 的第 $t$ 列。

边消除

将 $\mathcal{H}$ 中每一行最小的 $n-M$ 个元素设为0，记为 $\tilde{H}$。令 $\mathcal{H}’=\tilde{H}+\tilde{H}^T$，边消除如下

\[\mathbf{E}_{ij}=\begin{cases}1,&\text{if}\quad \mathcal{H}_{ij}^{\prime}=\mathcal{H}_{ji}^{\prime}>0\\0,&\text{otherwise}\end{cases}\]

这样可以缩小搜索空间。

Local Search

热图指导Best-first Local Search

通过 $f(node)$ 来评估最有希望的节点，$f$ 是目标函数。

搜索树的每个节点都是一个完整的TSP解，初始化时会随机生成一个解，并用2-opt启发式改进，直到找不到更好的解。搜索树的展开方式是k-opt启发式，具体来说，用一系列的节点 $u_1,v_1,u_2,\cdots,u_k,v_{k+1}$ ~~（我不知道他是不是写错了，最后应该是 $v_k,u_{k+1}$ 吧）~~表示动作，其中 $v_{k+1}=u_1$ 确保其是一个合法的解。所有的边 $(u_i,v_i)$ 断开，$(v_i,u_{i+1})$ 连上。在这里，一旦选定了 $u_i$，$v_i$ 就确定了。每次扩容随机选择 $u_1$，然后确定 $v_1$，然后再选择 $u_{i+1}$：

如果 $u_{i+1}=u_1$，即形成了一个新的TSP回路，导致一个改进的解。
如果 $i\geq k$，则放弃这个动作，开始一个新的扩展动作，$k$ 是设定的移除最大边数，是一个超参数。
否则，根据热图随机选择 $u_{i+1}$。用 $N_{u,v}$ 表示边 $(u,v)$ 在搜索过程中总共选择的次数，选择边 $(u,v)$ 的概率为
\[L_{u,v}~=~{\mathcal H}_{u,v}^{\prime}+\alpha\sqrt{\frac{\log(S+1)}{N_{u,v}+1}},\]
其中，$\alpha$ 是超参数，$S$ 是local search展开的动作总数。第一项鼓励选择热图值高的边，第二项时选择多样化。在给定 $u$ 选择 $v$ 的时候，只考虑热图值最高的 $M$ 个城市。

在扩展的时候，选择 $f$ 最小的节点作为下一个搜索节点。对于每个搜索节点，最多展开 $T$ 个动作。如果这 $T$ 个找不到更好的解，会随机生成一个新的初始解，并开始另一轮局部搜索。

更新热图

借用了MCTS中反向传播的思想，用 $s$ 表示当前节点，用 $s’$ 表示下一个搜索节点，$L(s)$ 表示tour的长度，热图更新为：

\[\mathcal{H}_{v_i,u_{i+1}}^{\prime}=\mathcal{H}_{v_i,u_{i+1}}^{\prime}+\beta[\exp(\frac{L(s)-L(s')}{L(s)})-1],\]

$\beta$ 是搜索参数。

利用随机

在展开的 $T$ 个动作找不到更好的解的时候，会随机修改参数 $K$。随机性在local search中被证明是非常强大的，有时需要更大的 $K$ 来获得更多初始解，有时候需要更小的 $K$ 进行深入探索。

实验

主实验

2000个实例用于训练，1000个用于评估。

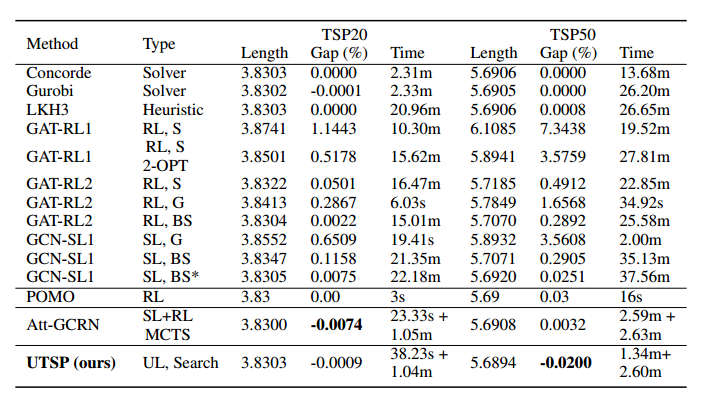
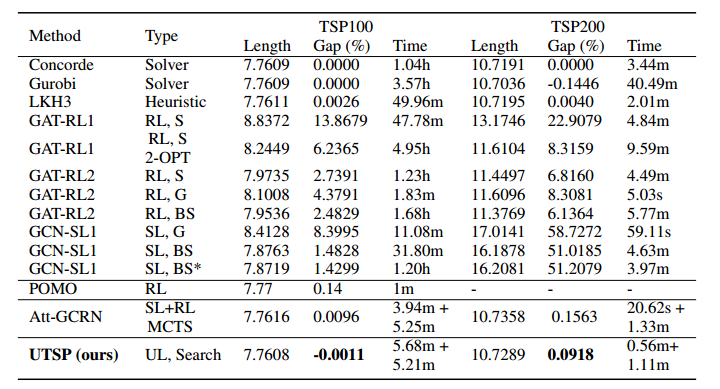
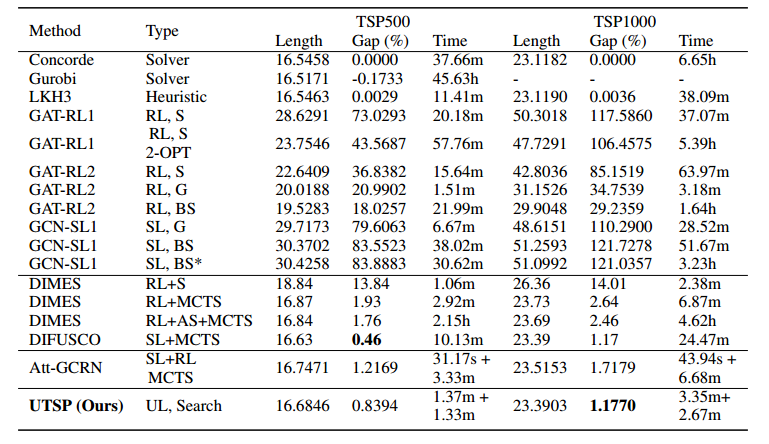
隐藏层只有64，训练参数只有44392个，RL大改需要70w个，SL也需要35w个。TSP100的训练时间只需要30分钟，而其他方法至少需要1天。

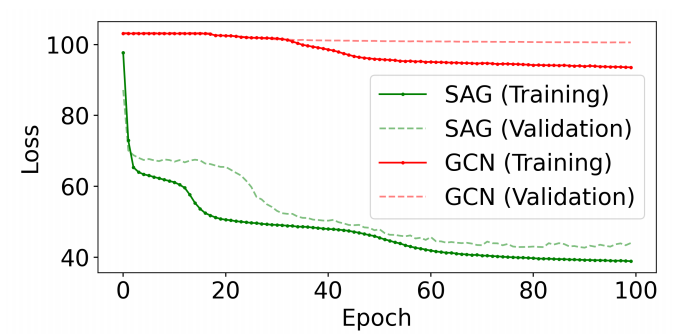
GNN的表达能力

能用更少的训练样本，有更强大的泛化能力。

低通GNN由于过度平滑产生的热图无法减少搜索空间，SAG本质上是一个带通滤波器。

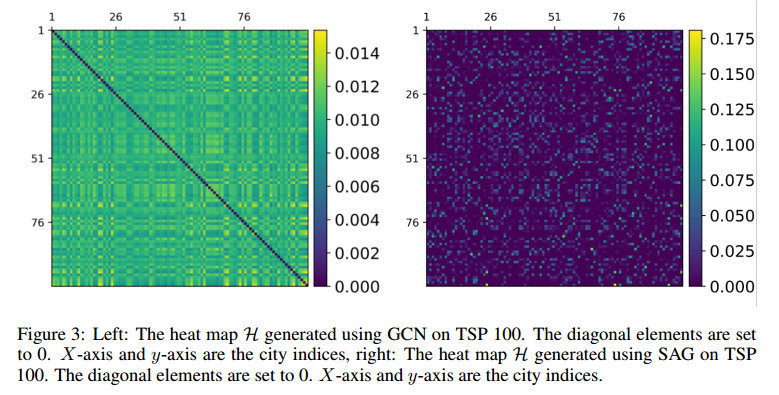
对角线是0，x轴和y轴是城市指数，这是热图的表达，左边是GCN的，右边是SAG的，SAG拥有更好的表达。

搜索空间规约

左图的纵轴表示边消除后，剩下的边的数量覆盖解决方案的程度，如果值为1表示成功覆盖所有的真实解的边。右图表示完全覆盖的实例数。

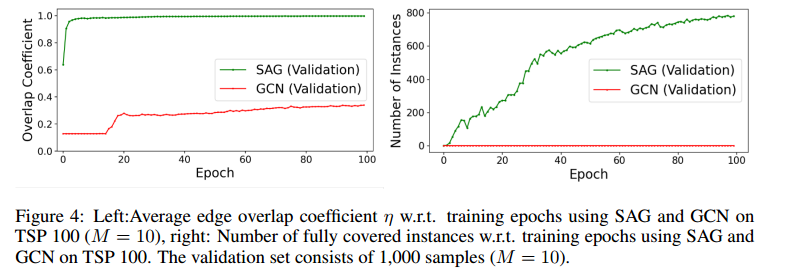
未来工作

扩展到更多的组合问题。