Unsupervised Learning Permutations for TSP using Gumbel-Sinkhorn Operator
基于Gumbel-Sinkhorn算子的TSP无监督学习置换
来自康奈尔大学
(这篇文章和NIPS23 Unsupervised Learning for Solving the Travelling Salesman Problem是同一个作者)
我个人觉得是这篇论文是对那篇论文的解释,没有提出什么新方法,都是解释性的。
摘要
机器学习社区最近对最佳传输(OT)表现出越来越大的兴趣。利用基于OT的熵正则化的方法已被证明对各种任务特别有效,包括排序,排序和解决拼图游戏Mena等,Adams和Zemel, Cuturi。在我们的研究中,我们扩大了熵正则化方法在NP-hard旅行商问题(TSP)中的应用。我们首先将TSP表述为识别长度最短的哈密顿环的置换。在此基础上,我们利用带熵正则化的Gumbel-Sinkhorn算子建立了排列表示。我们的发现表明了熵和泛化之间的平衡。我们将进一步讨论如何在不同的硬度上进行推广。
介绍
最优传输(OT)提供了一种结构化的方法来有效地将一个概率分布转移到另一个概率分布。
(前两段看不懂,后面的都是一些大差不差的TSP的介绍)
贡献
将TSP挑战重新表述为确定一个排列矩阵,该矩阵重新排序节点以产生最短的哈密顿循环。随后,采用了一种基于Gumbel-Sinkhorn算子的方法来学习这个置换矩阵。以一种无监督学习的方式训练模型,表明:
- 在熵和泛化之间存在权衡
- 通过调整Gumbel-Sinkhorn算子的参数,可以获得更好的泛化效果
- 讨论了一个更一般的场景,其中训练和测试数据可能来自不同的分布,基于在Gent和Walsh中观察到的相变现象,说明了从更困难的情况中学习的模型可以有效地扩展到更容易的情况
无监督学习TSP
作者的另一篇论文的内容
https://birdie-go.github.io/2024/01/24/Unsupervised-Learning-for-Solving-the-Travelling-Salesman-Problem/
简单来说,作者将邻接矩阵和节点二维坐标送进GNN后,将得到的结果 $h$ 进行softmax操作后,得到 $\mathbb{T}\in\mathbb{R}^{n\times n}$ 矩阵,接着用 $\mathbb{T}$ 去构建热图 $\mathcal{H}$
\[\mathcal{H}=\mathbb{T}\mathbb{V}\mathbb{T}^T\]其中
\[\mathbb{V}=\begin{pmatrix}0&1&0&0&\cdots&0&0&0\\0&0&1&0&\cdots&0&0&0\\0&0&0&1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\ddots&\vdots&\vdots&\vdots\\0&0&0&0&\ddots&1&0&0\\0&0&0&0&\cdots&0&1&0\\0&0&0&0&\cdots&0&0&1\\1&0&0&0&\cdots&0&0&0\end{pmatrix}\]$\mathbb{V}\in\mathbb{R}^{n\times n}$。$\mathcal{H}_{ij}$ 表示解决方案中边 $(i,j)$ 出现的概率。模型的损失函数表示为
\[\mathcal{L}=\lambda_1\underbrace{\sum_{i=1}^n(\sum_{j=1}^n\mathbb{T}_{i,j}-1)^2}_{\text{Row-wise constraint}}+\underbrace{\lambda_2\text{tr}(\mathcal{H})}_{\text{No self-loops}}+\underbrace{\sum_{i=1}^n\sum_{j=1}^n\mathbf{D}_{i,j}\mathcal{H}_{i,j},}_{\text{Minimize the distance}}\]$\mathbb{T}\rightarrow\mathcal{H}$ 是隐式将哈密顿回路的限制加入进热图中。
通过排列学习TSP
实际上,$\mathbb{T}$ 表示一般置换矩阵的近似值,它可以解释为交换节点动作序列的可微松弛。考虑一个简单的排列矩阵 $\mathbb{P}(q,t)\in\mathbb{R}^{n\times n}$ 交换了一个矩阵的第 $q$ 行和第 $t$ 行
\[\mathbb{P}(q,t)_{i,j}=\begin{cases}1,&\text{if }i=j\text{ and }(i\ne q)\text{ and }(i\ne t)\\1,&\text{if }i=q\text{ and }j=t\\1,&\text{ if }i=t\text{ and }j=q\\0,&\text{otherwise}\end{cases},\]将 $\mathbb{P}(q,t)$ 应用到矩阵 $A$ 上,$A$ 的第 $q$ 行和第 $t$ 行会交换,其他不变;当 $\mathbb{P}(q,t)$ 后乘到矩阵 $A$ 上,$A$ 的第 $q$ 列和第 $t$ 列会交换,其他不变。即 $\mathbb{P}(q,t)A\mathbb{P}(q,t)^T=\mathbb{P}(q,t)A\mathbb{P}(q,t)$ 表示 $A$ 的第 $q$ 和第 $t$ 行和列交换。
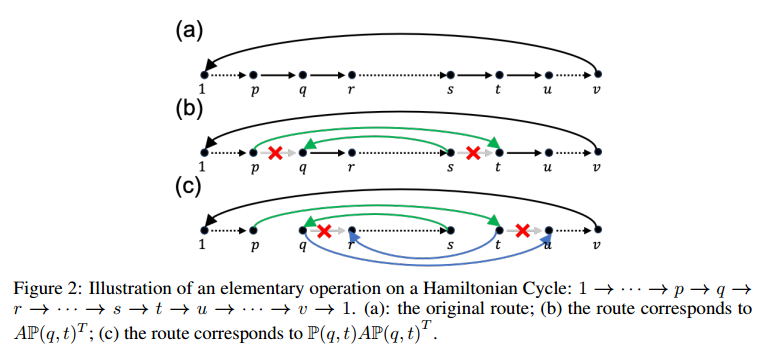
现在假设一个哈密顿回路 $1\rightarrow\cdots\rightarrow p\rightarrow q\rightarrow r\rightarrow\cdots\rightarrow s\rightarrow t\rightarrow u\rightarrow\cdots\rightarrow v\rightarrow 1$。矩阵 $A$ 的第 $q$ 行表示从第 $q$ 个城市出发的有向边的概率分布,第 $t$ 列表示以 $t$ 为终点的有向边的概率分布。当 $A\mathbb{P}(q,t)^T$,交换了节点 $q,t$。在图二b中,相当于删除了 $(p,q),(s,t)$ 并添加了 $(p,t),(s,q)$。在此基础上,$\mathbb{P}(q,t)A\mathbb{P}(q,t)^T$ 的结果会变成图二c,即 $(q,r),(t,u)$ 被删除且 $(q,u),(t,r)$ 被添加。因此,$\mathbb{P}(q,t)A\mathbb{P}(q,t)^T$ 表示交换了哈密顿回路中 $q,t$ 的子节点和父节点,其他保持不变,不会引入新的子环,仍然满足哈密顿回路。
上文提到,$\mathbb{T}$ 是置换矩阵的可微松弛,因为任何置换矩阵都可以分解成一个初等置换矩阵的排列,因此 $\mathbb{T}$ 可以解释称一系列节点交换动作的概率松弛。现在回顾第一条方程,如果把 $\mathbb{V}$ 想象成一张热图,其可以表示一个哈密顿回路 $(1,2,3,\cdots,n,1)$,目标是找到一个交换节点的排列,从而产生最短的哈密顿回路。$\mathbb{T}\rightarrow\mathcal{H}$ 给出了哈密顿回路的节点交换的概率表示。
使用Gumbel-Sinkhorn算子构建置换矩阵
Sinkhorn算子
Sinkhorn算子 $S(X)$ 对 $X\in\mathbb{R}^{n\times n}$ 可以写成
\[\begin{array}{rcl}S^0(X)&=&\exp(X),\\S^l(X)&=&\mathcal{T}_c\left(\mathcal{T}_r(S^{l-1}(X))\right),\\S(X)&=&\lim_{l\to\infty}S^l(X).\end{array}\]其中 $\mathcal{T}_{r}(X)=X\otimes(X\mathbf{1}_{n}\mathbf{1}_{n}^{\top})$ 和 $\mathcal{T}_{c}(X)=X\otimes(\mathbf{1}_{n}\mathbf{1}_{n}^{\top}X)$ 为矩阵的逐行和逐列归一化算子,$\otimes$ 表示逐元素除法,$\mathbf{1}_{n}$ 是全1列向量。
构建Gumbel-Sinkhorn分布
通过向Sinkhorn算子引入Gumbel噪声来构建置换矩阵的可微逼近,具体来说,研究表明可以通过温度相关的Sinkhorn算子构建置换矩阵的连续松弛
\[S(\frac{X+\epsilon}{\tau}),\]其中 $\epsilon$ 从Gumbel噪声中采样,$\tau$ 是温度,$S$ 是Sinkhorn算子。总的来说,有两个参数控制近似的熵。
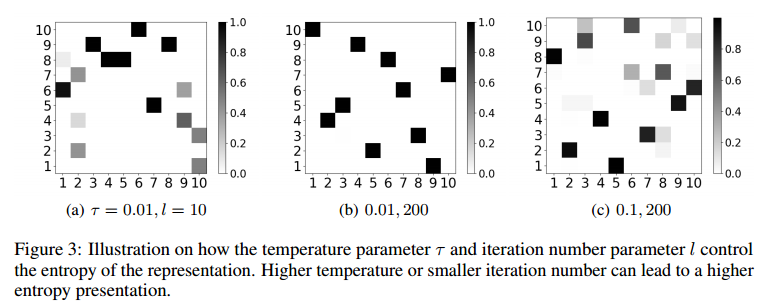
图三展示了随机输入矩阵在不同参数的Gumbel-Sinkhorn算子下10x10矩阵的样子,$l$ 是迭代的轮数。在本文的模型中,将GNN输出的结果 $h$ 进行该算子计算,$\mathbb{T}=S(\frac{h+\epsilon}{\tau})$,损失函数
\[\mathcal{L}=\lambda_1\lbrace\underbrace{\sum_{i=1}^n(\sum_{j=1}^n\mathbb{T}_{i,j}-1)^2}_{\text{Column-wise constraint}}+\underbrace{\sum_{j=1}^n(\sum_{i=1}^n\mathbb{T}_{i,j}-1)^2}_{\text{Row-wise constraint}}\rbrace+\underbrace{\lambda_2\text{tr}(\mathcal{H})}_{\text{No self-loops}}+\underbrace{\sum_{i=1}^n\sum_{j=1}^n\mathbf{D}_{i,j}\mathcal{H}_{i,j},}_{\text{Minimize the distance}}\]$\mathbb{T}$ 的熵实际上代表了节点交换的清晰度,低熵 $\mathbb{T}$ 意味不同节点之间的转换更加明显,有助于在搜索过程中更好进行节点交换决策。
熵和泛化的权衡
首先引入迪利克雷能量作为 $\mathbb{T}$ 熵的度量,以了解熵如何影响学习表征。迪利克雷能量能够平滑 $d$ 维表示 $f\in\mathbb{R}^{n,d}$,
\[E=\text{Trace}(f^T\triangle f),\]其中 $\triangle=I_n-D^{-1/2}WD^{-1/2}\in\mathbb{R}^{n\times n}$ 是图的拉普拉斯矩阵,$W$ 是邻接矩阵,$D$ 是图的度数矩阵。狄利克雷能量可以被解释为在图形顶点上定义的函数偏离常数的程度的度量。给定要给拉普拉斯矩阵,考虑其特征向量 $\psi_{1},\psi_{2},…,\psi_{n}$ 具有特征值 $\mu_{1}<\mu_{2}<…<\mu_{n}$,$\psi_1$ 表示常数函数,随后的特征向量对应越来越震荡的模式。函数越光滑对应了图结构有更低的迪利克雷能量和更高的熵。
和这个作者的另一篇文章类似,将 $\mathcal{H}$ 中每一行最小的 $n-M$ 个元素设为0,记为 $\tilde{H}$。 令 $\mathcal{H}’=\tilde{H}+\tilde{H}^T$,边消除如下
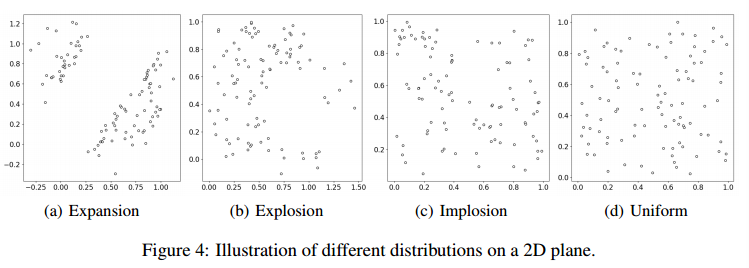
\[\mathbf{E}_{ij}=\begin{cases}1,&\text{if}\quad \mathcal{H}_{ij}^{\prime}=\mathcal{H}_{ji}^{\prime}>0\\0,&\text{otherwise}\end{cases}\]然后,在四种不同的分布上训练和测试模型:膨胀、爆炸、内爆和均匀。这四种分布的可视化表示如图4所示。在TSP 100数据集上实验了不同的 $\tau$ 和 $l$,导致模型中的熵(平滑)水平不同。随后,在4种不同的分布上对这些模型进行了评估。
实验结果如图5所示,x轴表示迪利克雷能量,y轴表示边消除后的集合和真实边集重合的比例,每个分布使用了1000个测试样本
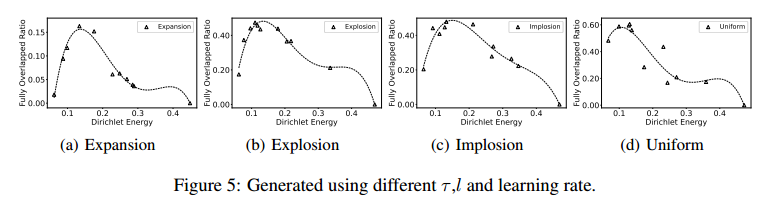
当狄利克雷能量较低时,所得热图的信息量就会减少,这表明具有同等可能的交换动作的高熵表示。当Dirichlet能量较大(> 0.3)时,表明处于低熵状态,模型不再是一系列节点交换动作的软松弛。相反,它只能生成很少的交换操作,这也损害了泛化。研究结果表明,低狄利克雷能量(高熵)和高狄利克雷能量(低熵)都会损害模型的泛化能力。为了获得最佳的泛化性能,控制表征的平滑性是至关重要的。
硬度泛化
图5还显示了不同分布表现出不同程度的泛化能力,膨胀分布的重叠比例为0.15,而爆炸分布能达到0.5。这里的目标是从一个分布中借用的一个模型,利用他来提高另一个分布的重叠率。
TSP Difficulty and the Phase Transition
首先要给不同分布定义一个描述符,以描述模型对于这个分布的表现。
有研究表明,计算难度通常与Phase Transition(相变?)有关。有学者曾经定义过难度参数
\[\gamma=(l_{opt}/\sqrt{nA}-0.78)n^{1/1.5},\]$l_{\text{opt}}$ 表示最佳解的旅行长度,$n$ 是节点数量,$A$ 是实例覆盖的面积。通过对不同实例的测试,$\gamma$ 的均值是0.58。本文计算了不同分布的难易级别,从简单到困难依次是:膨胀-爆炸-内爆-均匀,如图六a所示。
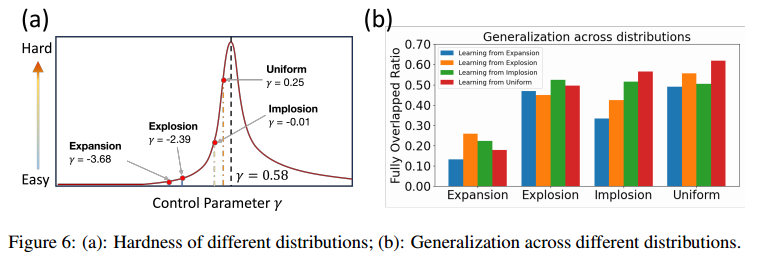
在TSP100中评估了四种分布的泛化能力,如图六b所示,y轴表示边集重合比。研究表明,直接在简单的分布上面学习会导致缺乏泛化能力,而在困难的分布熵学习不仅可以学习自己,还可以泛化到简单的分布。
采用作者另一篇提到的局部搜索方法来获取最终解后,实验结果如表1所示。