A linearithmic heuristic for the travelling salesman problem
European Journal of Operational Research 2021
University of Applied Sciences of Western Switzerland
方法

RecorderPath

-
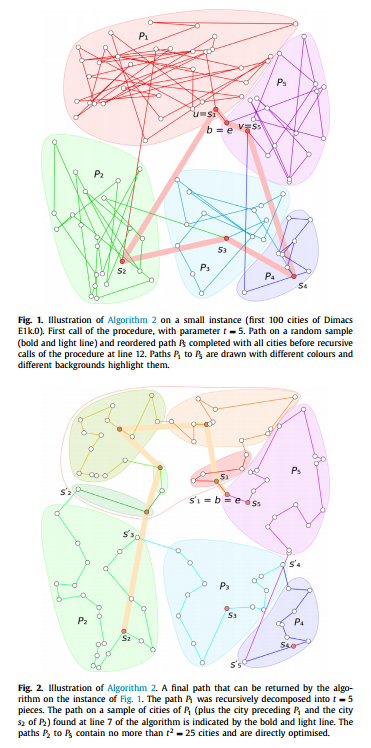
输入:$P=(b=c_i,c_1,\cdots,c_{i-1},c_{i+1},\cdots,c_n,c_i=e)$,超参数 $t$,一般取 10-20。
-
需要:OptimisePath,能够得到一条最优的路径(已知起点和终点),至少需要百级的
- 如果 $P$ 的规模小于 $t^2$,直接放进 OptimisePath 能够得到最优解。
- 找到距离 $b$ 最近的节点 $u$,找到距离 $e$ 最近的节点 $v$,然后再剩下的节点中随机挑出 $t-2$ 个。
- 将 $t-2$ 个节点和 $u,v$ 放进 OptimisePath,得到最优路径 $P_S=(b,s_1,\cdots,s_t,e)$。
- 然后对于在 $P$ 中但是不在 $P_S$ 中的节点,找到在 $P_S$ 中最接近的一个节点,放在他后面。
- 现在得到了 $P1=(b=s_1,\cdots,s_2),P2=(b=s_2,\cdots,s_3),\cdots$,对每一段分别再做一次 RecorderPath。
FastPopmusic
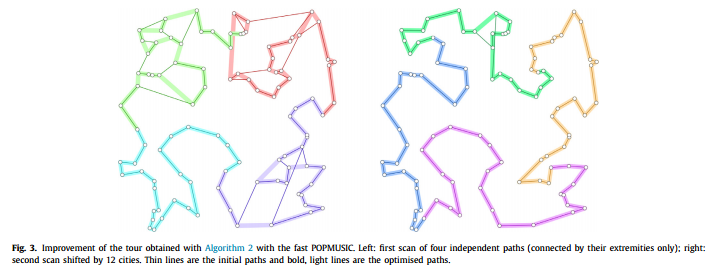
对 RecorderPath 得到的路径 $P$,每隔 $t^2$ 个就重新做一次 RecorderPath ,直到没得更新为止。