Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances

将一个小的预训练模型推广到任意大的TSP实例

AAAI2021

代码：https://github.com/Spider-scnu/TSP

（用到的 k-opt 和NIPS23有一篇很相似）

摘要

对于旅行商问题(TSP)，现有的基于监督学习的算法严重缺乏泛化能力。为了克服这一缺点，本文尝试(以监督的方式)训练一个小规模模型，该模型可以重复用于为任意大尺寸的TSP实例构建热图，基于一系列技术，如图采样，图转换和热图合并。此外，热图被输入到强化学习方法(蒙特卡洛树搜索)中，以指导搜索高质量的解决方案。基于大量实例(多达10,000个顶点)的实验结果表明，这种新方法明显优于现有的基于机器学习的TSP算法，并且显著提高了训练模型的泛化能力。

介绍

贡献

首先，基于带有注意机制的图卷积残差网络(AttGCRN)，通过监督学习训练一个小规模(大小为m)的模型。经过良好训练后，给定一个具有m个顶点的TSP实例，该模型能够在边缘上构建热图。然后，尝试将该模型平滑地推广到处理大型实例。为此，在给定大规模TSP实例的情况下，反复使用图采样方法提取具有恰好m个顶点的子图，然后将其转换为标准TSP实例，并调用预训练模型构建子热图。最后，将所有的子热图合并在一起，得到原始图上的完整热图。
此外，基于合并的热图，使用基于强化学习的方法，即蒙特卡罗树搜索(MCTS)来搜索高质量的解决方案。这里MCTS方法是一种基于转换的方法，其中每个状态都是一个完整的循环，每个动作将当前状态转换为一个新的完整循环。
结果：能解规模10000。

方法

预先工作

给定无向图 $G(V;E)$，其中 $\mid V \mid = n$，热图定义为一个 $n\times n$ 的矩阵 $P_{ij}\in[0,1]$，表示 TSP 解中包含这条路径的概率。

首先通过训练一个具有注意力机制的图卷积残差神经网络（Att-GCRN），输入大小固定为 $m$，训练集大小为 990000，标签为 Concorde 求解器得到的解。

Pipeline

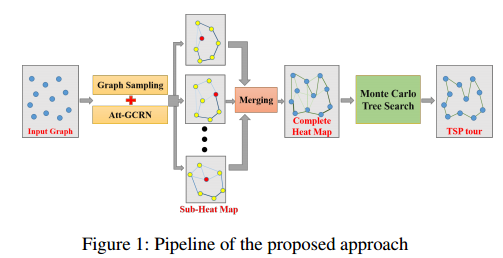
给定任意大尺寸的 TSP 实例，求解该实例的流程如图所示，主要包括三个步骤。

第一步(离线学习)分别采用图采样的方法从原始图中提取出若干个子图(每个子图恰好由m个顶点组成)，然后使用预训练的att - gcrn模型构建每个子图对应的子热图。
第二步尝试将所有的子热图合并成一个完整的热图(对应于原始图)。
第三步使用强化学习方法(在线学习)，即蒙特卡罗树搜索(MCTS)，在合并热图中存储的信息的指导下，搜索高质量的TSP解。

构建和融合热图

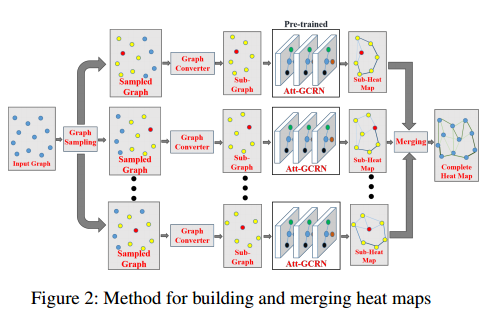
图采样

令 $O_i$ 或者 $O_{ij}$ 表示节点 $i$ 或者边 $ij$ 被采样的次数。

每次采样，选择 $O_i$ 最小的节点，如有相同随机选一个，将他作为聚类中心，使用KNN算法采样出一个具有 $m$ 个节点的子图，然后更新 $O_i$。

终止条件，最小的 $O_i$ 达到阈值 $\omega$。

图转化

训练集的所有节点都在一个正方形内，为了保证提取的节点也符合这个分布，需要进行转换。

公式就不列了，其实就是根据横纵坐标的 min 和 max 进行相应的拉伸。

构建子热图

用Att-GGRN。

融合子热图

重复以上几个步骤，可以得到 $I$ 个子热图。对于原始图像中的一条边 $(i,j)$，构建一个概率 $P_{ij}$ 表示最终这条边属于 TSP 解的概率

\[P_{ij}=\frac{1}{O_{ij}}\times \sum_{l=1}^{I}P^{\prime\prime}_{ij}(l)\]

$P^{\prime\prime}_{ij}(l)$ 表示第 $l$ 个子热图中 $(i,j)$ 的概率。其实就是加权平均。

最后将 $P_{ij}<10^{-4}$ 的边设置为 0。

强化学习用于解优化

马尔可夫决策过程

基于热图，采用强化学习搜索高质量的解决方案。

状态，一个解 $\pi=(\pi_1,\pi_2,\cdots,\pi_n)$
动作 $a$，将 $\pi$ 转换成 $\pi^\ast$。一个动作其实是一个 k-opt，即删除 k 条边，再新增 k 条边。

具体可以表示成，$a=(a_1,b_1,a_2,b_2,\cdots,a_k,b_k,a_{k+1})$，表示
- $a_1=a_{k+1}$
- 删除 $k$ 条边 $(a_i,b_i)$
- 加入 $k$ 条边 $(b_i,a_{i+1})$
- $b_i$ 不是可选的，一旦 $a_i$ 确定，$b_i$ 唯一确定。
这样，一个 k-opt 可以被拆解成 k 个动作，即选择 k 个 $a_i$。

值得注意的是，一些 $P_{ij}<10^{-4}$ 不在 $(b_i,a_{i+1})$ 的动作空间内。
奖励，两个解的 tour length 差值。

这样设计保证了：

动作空间从 2k 下降为 k；
结果必然是可行解。

初始解

从一个随机点出发，根据 $P_{ij}$ 采样下一个节点。

扩大邻域内的目标采样

当小邻域没有可以改进的方案时，扩大 k。

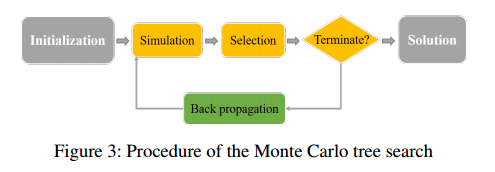
按照这个思路，选择蒙特卡洛树搜索作为学习框架。

初始化：定义两个 $n\times n$ 的矩阵，权重矩阵 $W_{ij}=100\times P_{ij}$ 控制在 $i$ 之后选择 $j$ 的概率，访问矩阵 $Q_{ij}=0$ 记录沿 $(i,j)$ 模拟时选择的值；变量 $M=0$ 记录已经模拟的操作总数。
模拟：动作 $a=(a_1,b_1,a_2,b_2,\cdots,a_k,b_k,a_{k+1})$ 包含一系列决策 $a_i$，一旦 $a_i$ 确定，$b_i$ 会被唯一确定；而一旦 $b_i$ 确定，可以根据可能性矩阵 $Z_{b_ij}$ 选择边 $(b_i,j)$（值越大，选择概率越高）
\[Z_{b_i j}=\frac{W_{b_i j}}{\Omega_{b_i}}+\alpha \sqrt{\frac{\ln (M+1)}{Q_{b_i j}+1}}\]
其中
\[\Omega_{b_i}=\frac{\Sigma_{j\neq b_i}W_{b_ij}}{\Sigma_{j\neq b_i}1}\]
表示所有与 $b_i$ 相连的边的权重矩阵平均值。

等式的第一部分强调了权重的重要性，第二部分更倾向于更少检查的边，$\alpha$ 用于强化和多样性之间的平衡参数。

决策顺序为：
- 随机选择 $a_1$，被删除的边 $b_1$ 被唯一确定；
- 如果决策长度足够，则 $a_{i+1}=a_1$；否则，考虑 $W_{b_ij}\geq 1$ 的顶点作为候选顶点集合 $X$，在候选集合中根据 $P_j$ 选择 $j$ 作为 $a_{i+1}$
  \[P_j=\frac{Z_{b_ij}}{\Sigma_{l\in X}Z_{b_il}}\]
  一旦 $a_{i+1}=a_1$，或者动作数量达到上限，就终止。
选择：在上述仿真过程中，如果满足改进动作，则选择改进动作并应用于当前状态 $\pi$，得到新的状态 $\pi^{new}$。否则，如果采样池中不存在这样的动作，那么在当前搜索区域内似乎很难获得改进。然后，MDP跳转到一个随机状态(使用上面描述的状态初始化方法)，该状态作为一个新的起始状态。
反向传播：$M,Q,W$ 都需要被更新。
- 当一个动作被检查，$M+1$；
- 当一个边 $(b_i,a_{i+1})$ 被检查，$Q_{b_ia_{i+1}}+1$；
- 当状态 $\pi$ 被修改成更好的 $\pi^{new}$，对于动作中的每一个 $(b_i,a_{i+1})$，更新
  \[W_{b_i a_{i+1}} \leftarrow W_{b_i a_{i+1}}+\beta\left[\exp \left(\frac{L(\boldsymbol{\pi})-L\left(\boldsymbol{\pi}^{n e w}\right)}{L(\boldsymbol{\pi})}\right)-1\right] .\]
  其中 $\beta$ 控制增长率。
- $Q,W$ 是对称矩阵。
- 当然不好的 $\pi$ 也可能存在好的边，但是为了避免错误的更新，仅当修改为更好的状态的时候才更新。
终止状态：搜索时间超过了由参数 $T$ 控制的允许时间。

实验

python写的热图构建，C++实现的MCTS，实验设备一个GTX 1080 Ti GPU，一台Intel(R) Xeon(R) Gold 5118 CPU @ 2.30GHz(8核)。

数据集

set 1：三个子集，每个子集包含10000个规模为 20 50 100 的 TSP 实例；
set 2：一共 400 个实例，包含 128 个规模为 200 500 1000 以及 16 个规模为 10000。

超参数

采样子图大小 $m=20/50$ 分别对应 set 1 和 set 2。

每条边采样次数 $\omega=5$。

参数 $\alpha=1,\beta=10,H=10n$。

MTCS 时间 $T=10n/40n$ 毫秒分别对应 set 1 和 set 2。

结果

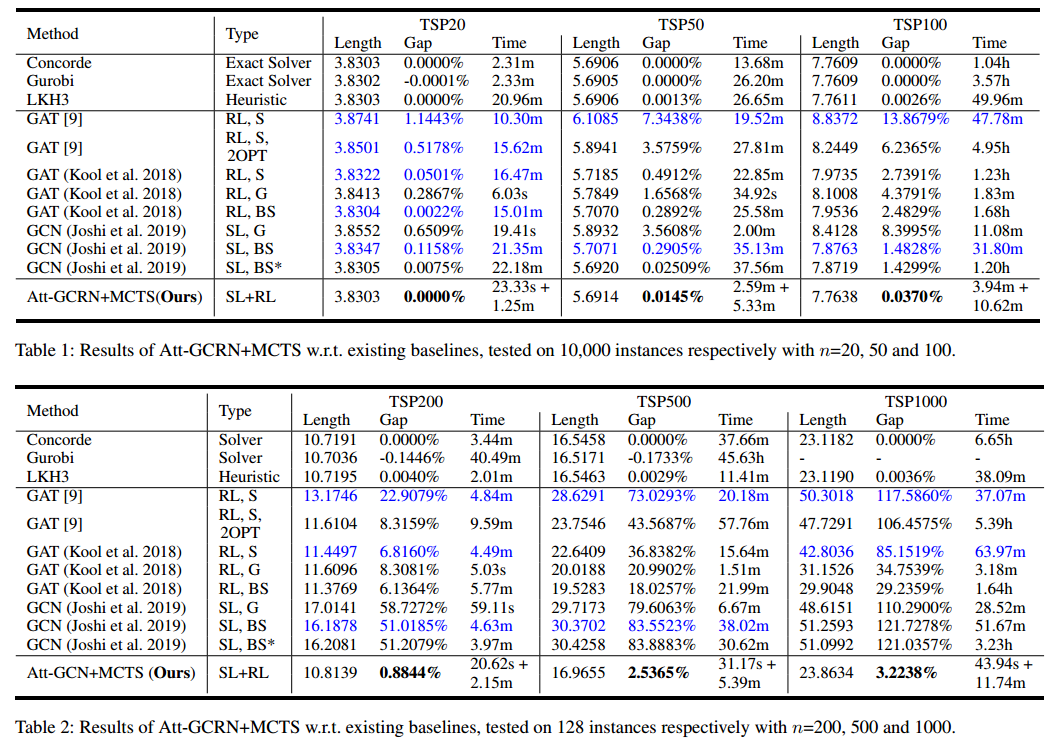
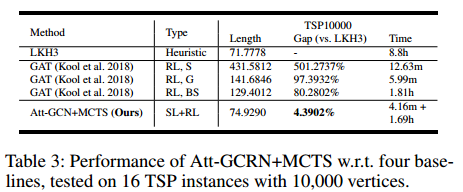
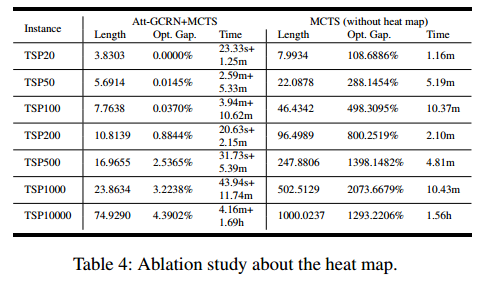
消融实验

把 Att-GCRN消去，变成每条边概率相等。