EFFICIENT TRAINING OF MULTI-TASK COMBINAROTIAL NEURAL SOLVER WITH MULTI-ARMED BANDITS
使用多臂赌博机(MAB)高效训练多任务神经组合优化求解器

https://arxiv.org/abs/2305.06361
(没太仔细研究,在看MVMoE: Multi-Task Vehicle Routing Solver with Mixture-of-Experts的时候看到他提到这个多任务方法看的)
摘要
有效地训练多任务神经解算器求解各种组合优化问题,迄今为止研究较少。在本文中,我们提出了一种通用的、高效的基于多臂强盗的训练范式,以提供一个统一的组合多任务神经求解器。为此,我们采用编码器-解码器框架下的多任务理论损失分解,通过任务内影响矩阵通过适当的强盗任务采样算法实现更有效的训练。与标准训练计划相比,我们的方法在有限的训练预算或相同的训练周期下实现了更高的整体性能,这可以为其他多任务大型模型的有效训练提供建议。此外,影响矩阵可以为学习优化领域的一些常见做法提供经验证据,从而支持我们方法的有效性。
介绍
针对的问题:TSP、CVRP、OP和KP(背包)
贡献:
- 提出一个通过MAB高效训练多个cop的组合神经求解器的新框架,该框架在训练资源有限的标准训练范式下取得了突出的表现,并可以进一步为其他大型模型的高效训练提供建议
- 研究编码器-解码器架构的理论损失分解,得到反映固有任务关系的影响矩阵和合理奖励,指导MAB算法的更新
- 验证了以前工作中对神经求解器的几个经验观察,通过影响矩阵,证明了方法的有效性和合理性
相关工作
- COPs神经求解器
- 多任务学习:旨在通过联合训练单个模型来提取多个任务之间的共享知识,从而提高多个任务的性能。一些研究的重点放在了任务分组上,其目标是识别任务关系和群体内的学习,以减轻冲突任务中的负迁移效应。
- 多臂赌博机
方法
考虑 $K$ 个COPs,表示成 $T^i(i=1,2,\cdots,K)$,每个问题有 $n_i$ 种不同的问题规模,整个任务集合为 $\mathcal{T}=\cup_{i=1}^K T^i={T^i_j\mid j=1,2,\cdots,n_i,i=1,2,\cdots,K }$。
求解器 $S_{\Theta^i}(\mathcal{I}_j^i):T_j^i\rightarrow \mathcal{Y}_j^i$,其中 $\Theta^i=(\theta^{share},\theta^i)$ 是COP $T^i$ 的参数,$\mathcal{I}_j^i,\mathcal{Y}_j^i$ 分别是输入和输出。目标函数
\[\min_{\Theta}L(\Theta)=\sum_{i=1}^{K}\sum_{j=1}^{n_i}L_j^i(\Theta^i)\]为了解决上式,根据MAB选择一个手臂 $a_t\in\mathcal{T}$,并产生奖励 $r_t$。

LOSS的讨论
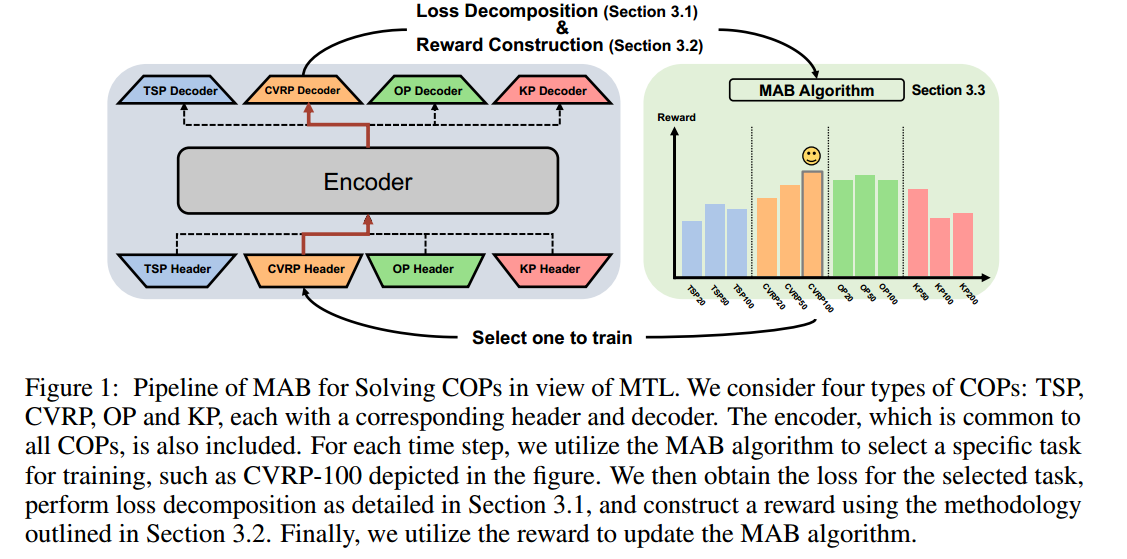
假设一个有意义的奖励应该满足以下两个性质
- 它有利于我们的目标并揭示内在的训练信号
- 当一项任务被选择时,期望中总会对其产生积极的影响

分成了三个部分:
- 同一个规模下的同一个问题,对 $\Theta_i$ 正面影响
- 不同规模下的同一个问题,对 $\Theta_i$ 产生负面影响
- 不同规模下的不同问题,对 $\theta^{share}$ 产生负面影响
奖励设计和影响矩阵构建
不同任务的梯度内积在尺度上可能存在显著差异,这将严重误导多臂赌博机的更新,因为即使梯度几乎是正交的,也可能来自较大的梯度值。为了解决这个问题,建议使用余弦度量来衡量任务对之间的影响。

然后就设计奖励和构建影响矩阵

实验
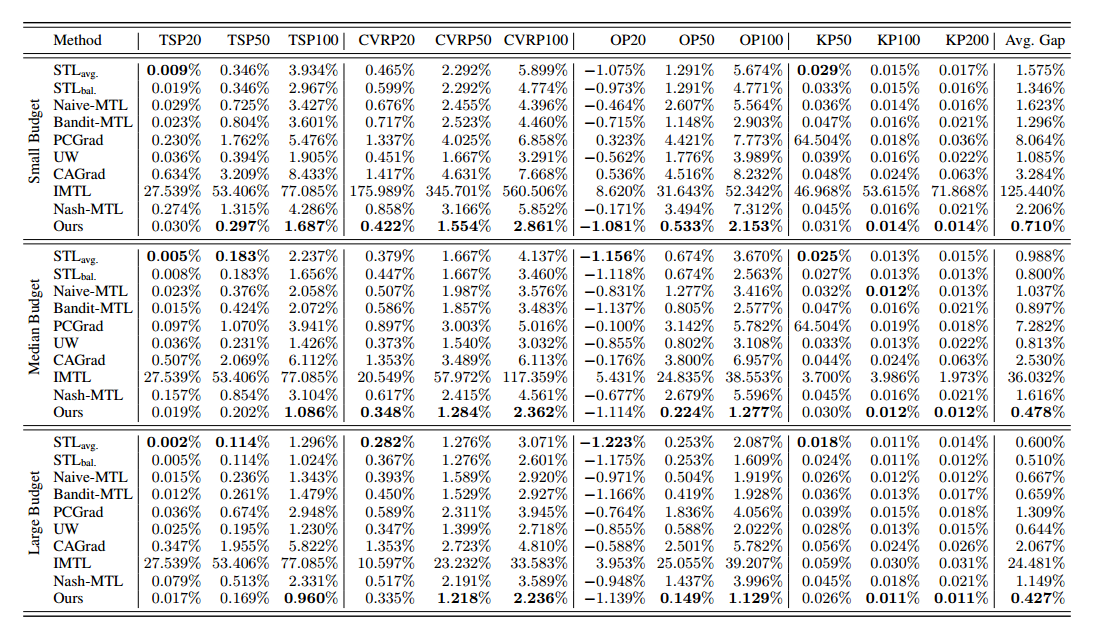
提出的方法与单任务训练(STL)和广泛多任务学习(MTL)方法进行了比较分析,以证明方法在不同评估标准下解决各种cop的有效性。具体来说,研究了两种不同的场景
- 在相同的训练预算下,目标是展示在自动获得多个cop的通用组合神经解算器方面的便利性,避免了MTL中平衡损失和STL中每个任务分配时间的挑战
- 给定相同数量的训练周期,试图说明可以推导出具有出色泛化能力的强大神经求解器。此外,利用影响矩阵分析了不同COP类型与不同问题尺度下相同COP类型之间的关系。
实验设置
STL对单个问题单个规模训练时间的总和等同于MTL的训练时间。