MVMoE Multi-Task Vehicle Routing Solver with Mixture-of-Experts

MVMoE: Multi-Task Vehicle Routing Solver with Mixture-of-Experts

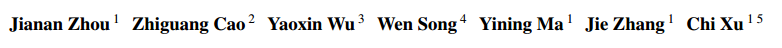
代码：https://github.com/RoyalSkye/Routing-MVMoE

摘要

学习求解车辆路径问题(vrp)已经引起了人们的广泛关注。然而，大多数神经解算器仅针对特定问题进行结构化和独立训练，这使得它们不那么通用和实用。在本文中，我们的目标是开发一个统一的神经求解器，可以同时处理一系列VRP变量。具体来说，我们提出了一种混合专家(MVMoE)的多任务车辆路径求解器，它在不增加计算量的情况下大大提高了模型的容量。我们进一步为MVMoE开发了一种分层门控机制，在经验性能和计算复杂性之间提供了良好的权衡。在实验中，我们的方法显著提高了10个未见过的VRP变量的零射击泛化性能，并在少数射击设置和现实世界的基准测试实例上展示了不错的结果。我们进一步对MoE配置在求解vrp中的作用进行了广泛的研究，并观察到分层门控在面对分布外数据时的优越性。

介绍

目标：开发一个统一的神经求解器，可以同时求解一系列VRP问题变形，并且在未见过的VRP问题上有良好的zero-shot泛化能力。

已有研究

• Wang, C. and Yu, T. Efficient training of multi-task neural solver with multi-armed bandits. arXiv preprint arXiv:2305.06361, 2023.

  多臂赌博机的应用

  博客：https://birdie-go.github.io/2024/05/15/EFFICIENT-TRAINING-OF-MULTI-TASK-COMBINAROTIAL-NEURAL-SOLVER-WITH-MULTI-ARMED-BANDITS/

• Lin, Z., Wu, Y., Zhou, B., Cao, Z., Song, W., Zhang, Y., and Senthilnath, J. Cross-problem learning for solving vehicle routing problems. In IJCAI, 2024.

  通过有效的微调，是在一个基本VRP上与训练的模型适应目标VRP。

  缺点：由于依赖于针对预定问题变体构建的网络，它们无法实现对未知vrp的零射击泛化。

• Liu, F., Lin, X., Zhang, Q., Tong, X., and Yuan, M. Multi-task learning for routing problem with cross-problem zero-shot generalization. arXiv preprint arXiv:2402.16891, 2024

  通过组合zero-shot学习赋予神经求解器这种通用性，它将VRP变体视为一组底层属性的不同组合，并使用共享网络来学习它们的表示。

  缺点：它仍然利用了现有的简单vrp网络结构，受其模型容量和经验性能的限制。

提出混合专家（Mixture-of-Experts，MoE）层代替Transformer中的FFN，这些专家是一组具有各自可训练参数的FFN。MoE通过门控网络路由到特定的专家，并且激活特定专家中的参数。

贡献

1. 提出了一种统一的神经解算器MVMoE来求解多个vrp，首次将moe引入到cop的研究中。唯一的MVMoE可以在不同的VRP变体上进行训练，并在未见过的VRP上提供强大的零射击泛化能力。
2. 为了在经验性能和计算开销之间取得良好的平衡，开发了MVMoE的分层门控机制。令人惊讶的是，它表现出比基门控更强的分布外泛化能力。
3. 大量的实验表明，MVMoE在10个未见过的VRP变量上显著提高了对基线的零射击泛化，并且在少射击设置和现实世界实例上取得了不错的结果。进一步对MoE配置(如MoE位置、专家数量和门控机制)对零射击泛化性能的影响进行了广泛的研究。

相关工作

• 神经VRP求解器：两种主流
  • 构造：自回归（指针网络，应用RL探索TSP和CVRP，AM，POMO，其他都说在AM和POMO上开发的），非自回归（热图）
  • 改进
• 混合专家

Preliminaries

VRP变种

• 容量限制 $C$ （常驻）
• 开放路径 $O$，不需要返回终点
• backhaul $B$，容量可以为负数
• 持续时间限制 $L$，为了保持合理的负载，每条路的长度都有一个阈值
• 时间窗 $TW$

因此有 16 种变形。

训练方法：REINFORCE

方法

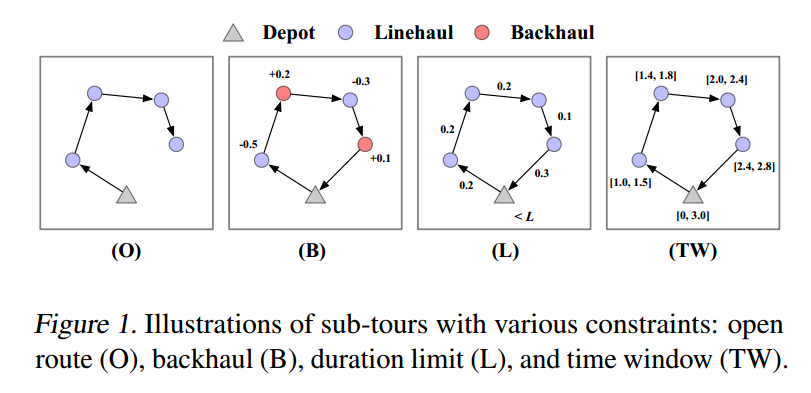
基于构造的求解器

实例的静态信息 $\mathcal{S}_i=\lbrace y_i,\delta_i,e_i,l_i\rbrace$ 分别表示坐标、需求、时间窗起点和终点

静态信息作为编码器的输入，输出 $d$ 维的节点embedding $h_i$

动态信息 $\mathcal{D}_i=\lbrace c_t,t_t,l_t,o_t\rbrace$ 表示剩余容量、当前时间、当前部分解的长度、开放路线的presence indicator

动态信息作为解码器的上下文信息，连同上一个节点一起提供给解码器

如果当前求解的VRP变体没有某个特征，如没有TW，就设置为 $\mathcal{S}_i=\lbrace y_i,\delta_i,0,0\rbrace$。这些变体的特征就是这些属性的不同组合，即zero-shot泛化能力。

混合专家

一个MoE层包括了

• $m$ 个专家 $\lbrace E_1,E_2,\cdots,E_m\rbrace$，每一个专家都是一个独立参数的FFN
• 带有参数 $W_G$ 的门控网络 $G$，决定了输入到专家的分布

给定输入 $x$，$G(x),E_j(x)$ 表示门控网络的输出（$m$ 维向量）以及第 $j$ 个专家的输出。MoE层可以表示为

向量 $G(x)$ 是稀疏的，他只会激活模型参数的一小部分专家，节省计算量。门控网络用一个 TOP-K 算子保留 $k$ 个最大的值而其他设置为负无穷来表示稀疏性

考虑到更大的稀疏模型并不总是带来更好的性能，设计有效和高效的门控机制以赋予每个得到充分训练的专家足够的训练数据是至关重要的，但也很棘手。为此，在语言和视觉领域已经提出了一些工作，例如设计辅助损失(Shazeer等人，2017)或将其表述为线性分配问题(Lewis等人，2021)，以追求负载平衡。

MVMoE

编码器和解码器都用MoE替换了FFN，解码器加更有效。损失函数

其中，$\mathcal{L}_{\alpha}$ 表示原有的VRP求解器中REINFORCE的损失，$\mathcal{L}_{\beta}$​ 表示关于MoEs的损失（这部分在附件）。$\alpha=0.01$​。

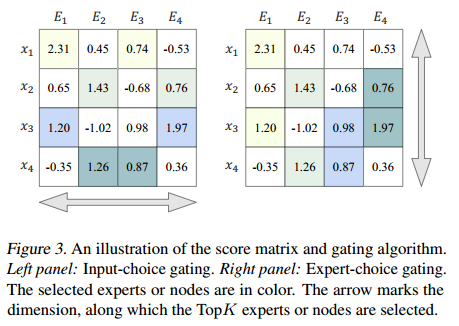
输入选择门控

Moe 层的输入是 $x\in\mathbb{R}^{I\times d}$，其中 $I$ 是总节点数；输出是分数矩阵 $H=(X\cdot W_G)\in\mathbb{R}^{I\times m}$。尽管应用了TopK，但是这种方法本身不能保证负载均衡，例如一个专家可能比其他专家得到更多的节点，导致一个占主导地位的专家，使得其他专家无法拟合。(Shazeer等人，2017)的工作使用了一个具有 Importance 和 Load 的噪声TopK门控来控制每个专家接收到相似数量的节点，具体来说

然而，接收到的节点的数量是离散的，不能作为损失通过反向传播更新网络，上述噪声项通过平滑估计器使梯度反向传播有助于负载平衡。然后，使用 Importance 和 Load 作为辅助损失来强制负载均衡

其中，$Importance(X)$ 和 $Load(X)$ 都是 $\mathbb{R}^m$，$\Phi$ 是标准正态分布的累计函数，$\varphi(a,b,c)$ 表示 $a$ 的第 $b$ 最大分量（不包括分量 $c$），$H’_x$ 表示 $H’$ 中 节点 $x$ 对应的向量，$CV$ 是变异系数。

专家选择门控

沿着 $H$ 的第一维应用 Softmax 得到 $P$，其中 $P[i,j]$ 表示 第 $i$ 个节点被第 $j$ 个专家选择的概率。这个矩阵一共有 $K=I\times \beta,(\beta=2)$ 个非零值，显式保证了负载均衡，且灵活（一个节点可以分配给不同数量的专家）。没有限制每个节点的最大专家数量，因为它需要解决一个额外的线性规划问题(Zhou et al, 2022)，从而增加了计算复杂性。

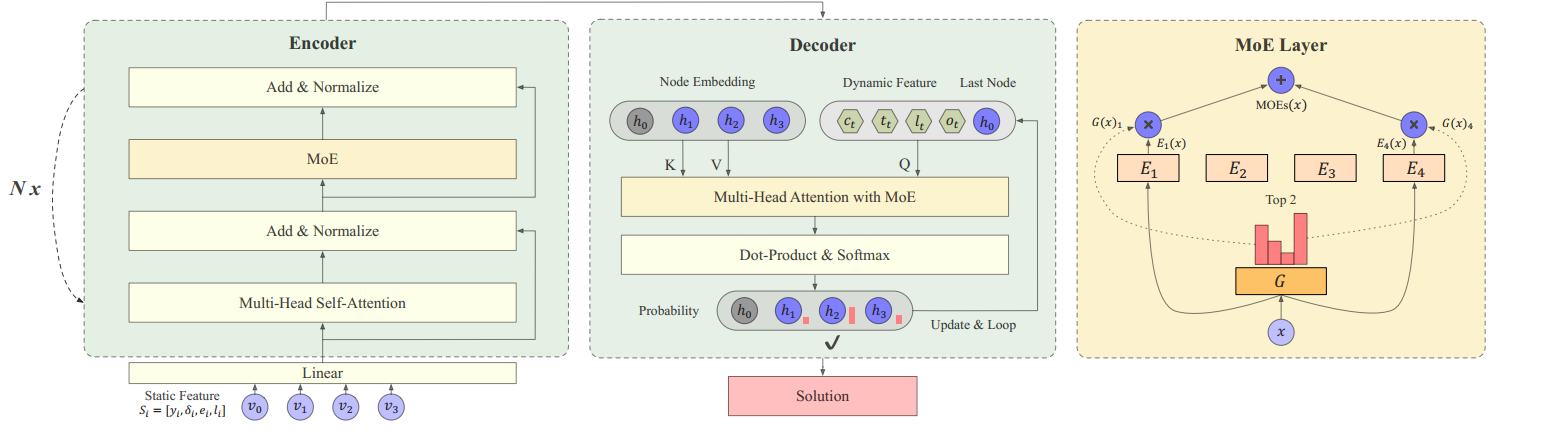
分层控制

在解码的时候，当问题规模增大，解码的步数也会增大，而且还需要算mask，这样在每次解码都使用MoE的计算成本很高，因此考虑只在部分解码步骤中使用MoE。

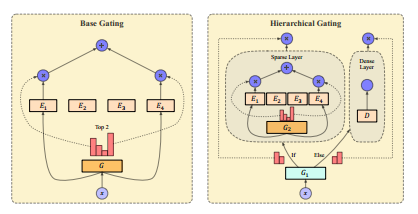
如图，分层控制有两个门控 $G_1,G_2$，$m$ 个专家 $E_{1\cdots m}$，一个dense层 $D$（比如线性层）。给定输入 $X\in\mathbb{R}^{I\times d}$，$G_1$ 选择将 $X$ 分配给密集层还是稀疏层。$G_1$ 的输出是 $G_1(X)=Softmax(X_1\cdot W_{G_1})\in\mathbb{R}^{1\times 2}$。简单来说，就是选择是经过MoE层还是普通的FFN层。

总体而言，分层门控提高了计算效率，但对经验性能的影响较小。

文章还探索了一种更高级的门控技术：From sparse to soft mixtures of experts. In ICLR, 2024.但实验证明在VRP上表现不好。

实验

baseline

• 传统求解器：HGS、LKH3、OR-Tools
• 神经求解器：POMO（单任务训练）、POMO-MTL（多任务训练）

训练问题集：CVRP, OVRP, VRPB, VRPL, VRPTW, and OVRPTW

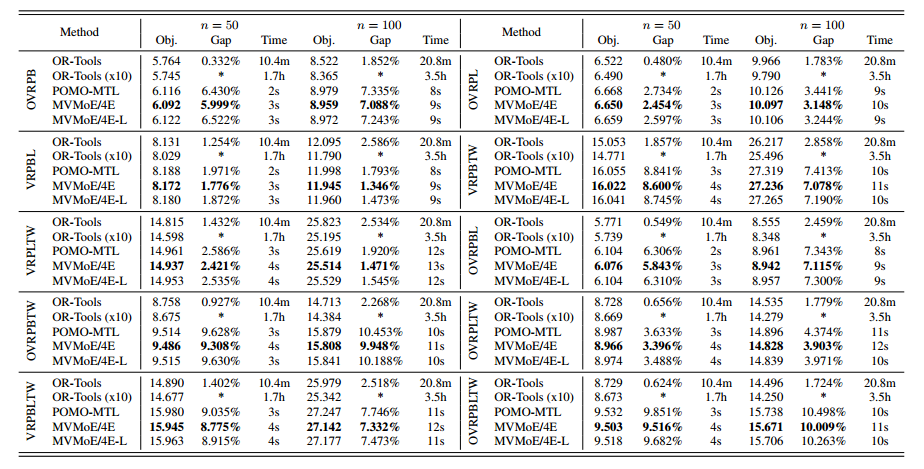
MVMoE-L表示轻量级，即用分层门控，4E表示4个专家。

消融实验和其他实验

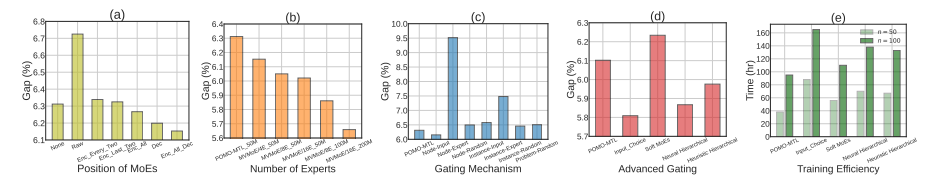
• MoE的位置：特征提取、编码器、解码器（结果表明，用在解码器效果很好，全部一起用效果更好，其他地方用效果不明显）
• 专家的数量：提升到8和16（越多越好，但参数也越多）
• 门控技术：node-input最好，node-expert最差，还在探索当中
• 考虑的最新的门控技术，第四个图，感觉效果不行
• 每种门控的训练时间，证明分层门控可以减少训练开销
• benchmark表现：在附件里面，在大规模上效果很差，仍未解决
• 可扩展性：在轻编码器重解码器的代码上实验了一下，效果非常好

附件里面还有很多实验

• Previous
  EFFICIENT TRAINING OF MULTI-TASK COMBINAROTIAL NEURAL SOLVER WITH MULTI-ARMED BANDITS
• Next
  Looking Ahead to Avoid Being Late Solving Hard-Constrained Traveling Salesman Problem