Looking Ahead to Avoid Being Late: Solving Hard-Constrained Traveling Salesman Problem
https://arxiv.org/abs/2403.05318v1
(我感觉整体一般)
摘要
许多现实问题都可以被表述为受限旅行商问题(TSP)。然而,约束条件总是复杂和众多的,使得求解tsp具有挑战性。当复杂约束数量增加时,传统的启发式算法为了避免不合理的结果而耗费大量时间。基于学习的方法提供了一种以软方式解决tsp的替代方法,它还支持GPU加速以快速生成解决方案。然而,这种软方式不可避免地导致学习算法难以解决硬约束问题,合法性与最优性之间的冲突可能会严重影响解的最优性。为了克服这一问题并有效地解决硬约束,我们提出了一种新的基于学习的方法,该方法使用前瞻性信息作为特征来提高具有时间窗(TSPTW)解的TSP的合法性。此外,我们还构建了带有硬约束的TSPTW数据集,以便对各种方法的统计性能进行准确评估和基准测试,为未来的研究服务。通过在不同数据集上的综合实验,MUSLA优于现有基线,显示出推广潜力。
介绍
缩写:MUlti-Step Look-Ahead(MUSLA)
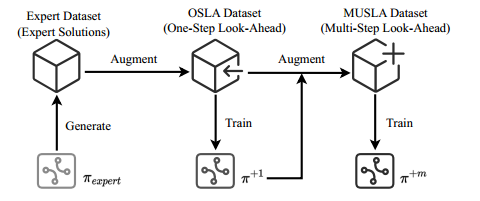
MUSLA引入了一种新颖的 one-step look-ahead 方法来收集有关约束边界的未来信息,并通过模仿专家来训练策略 $\pi^{+1}$。基于训练良好的策略,我们通过 multi-step look-ahead 信息收集来增强专家数据集。收集到的关于未来情况的信息可以更好地理解约束边界。利用增强的数据集,我们进一步训练了MUSLA策略 $\pi^{+m}$。
贡献:
- 提出了一种新的基于监督学习方法的前瞻机制。MUSLA通过增加带有搜索信息的数据集来增强SL解决方案的最优性和合法性。
- 设计了两种TSPTW数据集。
- 与最好的RL进行对比实验。
问题描述
问题
图 $\mathcal{G}=(V,E)$,点集 $V=\lbrace 0,1,\cdots,n\rbrace$,边集 $E\subset V\times V$。节点坐标 $a_i$,时间窗 $[t_i^s,t_i^e]$。边 $L_{i,j}=\mid\mid a_i-a_j\mid\mid_2$。解 $X=\lbrace x_0, x_1, x_2, \ldots, x_n\rbrace$。
目标函数:
\[\begin{gathered} \min _{X=\lbrace x_0, x_1, x_2, \ldots, x_n\rbrace } L_{x_n, x_0}+\sum_{i=0}^{n-1} L_{x_i, x_{i+1}} \\ \text { s.t. } t_{x_i}^s \leq t_i \leq t_{x_i}^e \end{gathered}\]把TSPTW看成多目标问题,最小化旅行距离和最小化违反约束。
监督学习
通过 $p(X\mid g)=\Pi_{i=0}^{n-1}p(x_{i+1}\mid X_{0:i},g)$ 得到 $X=\lbrace x_0, x_1, x_2, \ldots, x_n\rbrace$,$g$ 是实例。
最大似然估计
\[J(\theta)=\max _\theta \log p_{\pi_\theta}\left(X=X^* \mid g\right) .\]方法
利用 one-step look-ahead 机制增强专家数据集,并训练一个监督学习策略 $\pi_\theta^{+1}$。利用该策略,收集 multi-step look-ahead(MUSLA)信息,进一步细化专家数据集。
采用监督学习而不是强化学习
- 强化学习需要额外的奖励塑造来平衡两个目标(目标函数和合法性)
- 强化学习的计算负担很大
用动态信息学习
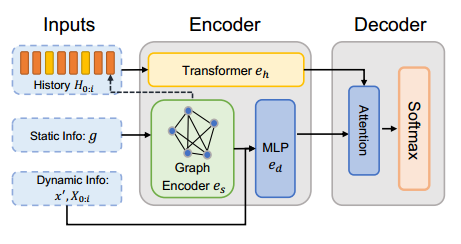
以往的研究采用静态信息 $I^s(g)=\lbrace a_i,t_i^s,t_i^e\rbrace$ 和历史信息 $I^h(X_{0:o})$。
设计了动态信息 $I^d(X_{0:i},x’,g)$,其中 $x’\in V\setminus X_{0:i}$。在距离维度上,有 $\lbrace L_{x’,x_i},a_{x’}-a_{x_i}\rbrace$;在时间维度上,有 $\lbrace t_{x’}^s-t_i,t_{x’}^e-t_i\rbrace$。
因此,概率向量表示为 $p(x=$ $\left.x^{\prime} \mid X_{0: i}, g\right)=\pi_\theta\left(x^{\prime}, I^s(g), I^h\left(X_{0: i}\right), I^d\left(X_{0: i}, x^{\prime}, g\right)\right)$。
数据增强
为了确定 $x’$ 是否应该是下一个节点,最暴力的判断合法性的方法就是从 $x’$ 开始搜索所有的方案。
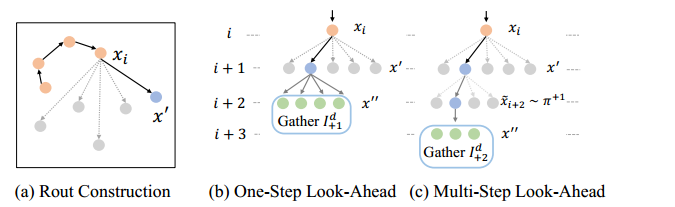
One-Step Look-Ahead(OSLA)
已有 $X=\lbrace x_0, \ldots, x_i\rbrace $,迭代所有未访问过的 $x’$ 去构造 $X’=\lbrace x_0, \ldots, x_i,x’\rbrace $,并收集信息 $I^d_{+1}(X’,g)$,其中 $x’‘\in V\setminus X’$。$I^d_{+1}$ 会作为动态信息帮助 $x’$ 的选择。
更详细地说,OSLA会包含两类value。
- 一类是迟到点,即所有无法在时间窗终点抵达客户节点的 $X’‘_{late}$。利用会迟到节点的数量以及最大迟到的时间作为特征来捕获选择 $x’$ 的约束违规。
- 第二类是假设 $X’‘_{late}$ 是空集,在贪婪访问时间开销最小的节点 $x’’$ 时,增加距离和时间开销。
通过增加的OSLA作为额外输入,学习OSLA策略 $\pi_\theta^{+1}(x’,I^d,I_{+1}^d)$。这些信息是通过专家solution收集的,不会给训练过程带来负担。
Multi-Step Look-Ahead with An OSLA Policy
One-Step 有助于了解约束边界,但不够。因此提出 MUSLA。
未来信息中,只收集专家选择概率最高的 $k$ 个节点 $x’$ 的未来信息。
使用 $\pi_\theta^{+1}$ 作为专家策略的近似,连续构造 $m$ 步得到 $\tilde{X}^{\prime}=\lbrace x_0, \ldots, x_i, x^{\prime}, \tilde{x}{i+2}, \ldots, \tilde{x}{i+1+m}\rbrace $。
在文章中,$k=5,m=1$,即通过动态信息 $I^d,I_{+1}^d,I_{+2}^d$ 作为数据增强,学习策略 $\pi_\theta^{+2}(x’,I^d,I_{+1}^d,I_{+2}^d)$。
最优性和合法性的权衡
允许稍微超时,即 $t_i’=t_i+\epsilon$。叫做MUSLA-adapt。
数据集
专家解决方案由LKH3给出。
-
Medium
- $a_i$ 在 $\mathcal{U}[0,100]^2$ 内随机采样。
- 时间窗起点 $t_i^s$ 在 $\mathcal{U}[0,T_n]$ 内采样,$T_n$ 是任意TSP在 $n+1$ 个节点上的期望距离,$T_{20}\approx 10.9$。
- 时间窗宽度 $T_n\cdot \mathcal{U}[\alpha,\beta]$。$\alpha,\beta$ 是两个超参数。
-
Hard
-
先按照Medium生成数据集。
- 随机选择 $\lfloor 0.3n\rfloor$ 个节点将其分成 $n_g$ 组,每一组用Medium的方式生成重构时间窗,时间窗加个偏移量,偏移量 $\mathcal{U}[0,T_n]$。
- 当 $n=20$,总组数是2;当 $n=50,100$,总组数 $\mathcal{U}[2,7]$。
-
-
补充数据集:缓解过拟合
- 例如去除左侧或者两侧的时间窗
- 分组,每一组的起始时间是上一组的最晚时间,组之间时间窗相互不覆盖
数据集大小,20、50、100。前两个规模数据集大小50w,大规模数据5w因为LKH3求解时间很长。
Mediun、Hard和补充数据集的数据比是1:1:3。
$\alpha=0.5,\beta=0.75$。
验证集Hard中,初始数据集所有时间窗均为 $[0,T_n]$,每一组的时间窗也是拉满的(看起来,除了分组没有时间窗)。
实验
Greedy-MT是选择最小路程的节点,Greedy-LT是选择最早抵达时间的节点。
JAMPR是做VRPTW的学习方法。
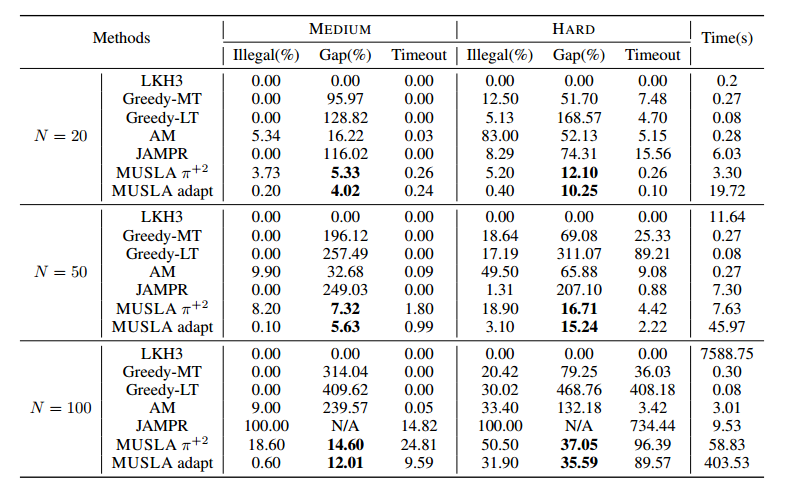
强化学习方法的总奖励是cost+timeout+超时节点数量。
最优性和合法性的平衡
\[S=\gamma \cdot \text { Illegal }+(1-\gamma) \cdot \text { Gap}\]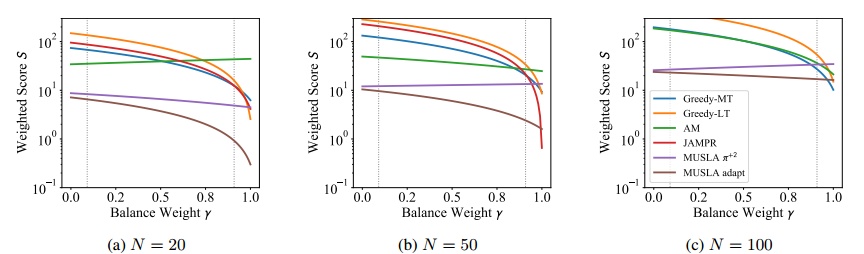
消融和泛化