SplitNet A Reinforcement Learning Based Sequence Splitting Method for the MinMax Multiple Travelling Salesman Problem

SplitNet: A Reinforcement Learning Based Sequence Splitting Method for the MinMax Multiple Travelling Salesman Problem

AAAI23

天津大学和华为诺亚方舟实验室

摘要

MinMax Multiple Travelling Salesman Problem(mTSP)是一类重要的组合优化问题，具有许多实际应用，其目标是使所有车辆的最长行程最小化。由于该问题的计算复杂度较高，现有的求解方法无法以较快的速度获得满意质量的解，特别是当问题规模较大时。在本文中，我们提出了一种基于学习的方法SplitNet，将单个TSP解转换为相同实例的MinMax mTSP解。具体来说，我们生成单个TSP解序列，并使用由强化学习训练的基于注意力的模型将它们分割成mTSP子序列。我们还为分裂策略设计了决策区域，大大减少了不同尺度实例上的策略动作空间，从而提高了SplitNet的泛化能力。实验结果表明，在广泛使用的不同规模的随机数据集和公共数据集上，SplitNet具有良好的泛化性能，优于现有的基于学习的基线和Google OR-Tools，求解速度快。

介绍

三类基于强化学习求解MinMax mTSP的方法

• 一种聚类的方式，采用分布式策略网络将节点分配到不同的集群，并采用元启发式方法获得每个集群的单个TSP解。

  Hu, Y.; Yao, Y.; and Lee, W. S. 2020. A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs. Knowledge-Based Systems, 204: 106244.

• 一个构造策略，基于Transformer的去中心化注意力网络（Decentralized Attention-based Neural Network, DAN），并使用RL对模型进行训练。

  Cao, Y.; Sun, Z.; and Sartoretti, G. 2021. DAN: Decentralized Attention-based Neural Network to Solve the MinMax Multiple Traveling Salesman Problem. arXiv preprint arXiv:2109.04205.

  Distributed Autonomous Robotic Systems (DARS 2022)

• 在上述DAN的基础上引入了类型感知的图注意，并提出了一种新的构造方法，可以有效地提取图中的特征。

  Park, J.; Bakhtiyar, S.; and Park, J. 2021. ScheduleNet: Learn to solve multi-agent scheduling problems with reinforcement learning. arXiv preprint arXiv:2106.03051.

  投了ICLR2022，被拒了。理由是贡献很小，改进很小，没啥理论依据。

这些基于RL的方法具有更快的速度和更强的泛化能力，但求解质量存在一定差距。

mTSP的最优解和TSP的最优解有63%到74%的重叠。

因此，一种直观的思路是直接拆分单个TSP序列，将暴露的结束节点与原始节点连接起来，得到mTSP解。基于此提出了一种名为SplitNet的方法，该方法通过拆分操作将单个TSP解转换为MinMax mTSP解，从而获得高质量的解。SplitNet的工作流程包括以下三个步骤

1. 生成：生成单个TSP解序列
2. 拆分：将每个单个TSP解序列拆分，将暴露的结束节点与原始节点连接，得到多个子序列，子序列个数等于车辆个数
3. 改进：改进每个子序列，进一步得到优化的MinMax mTSP解。

为了提高SplitNet在大规模MinMax mTSP上的泛化性能，进一步设计了决策域，以减小SplitNet的分割操作范围。

贡献：

• 基于单个TSP和mTSP最优解的相似性，提出了将单个TSP解序列转换为MinMax mTSP解序列的框架。
• 在上述框架下，设计了单个TSP解序列拆分模型和相应的RL训练方案。为了进一步提高分割模型的泛化能力，还设计了决策域来减少分割动作空间。
• 实验比较：更优性能、更快速度。

问题描述

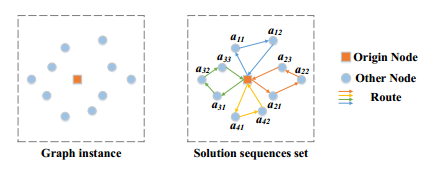
目标函数是让最长的路径最短的VRP。

方法

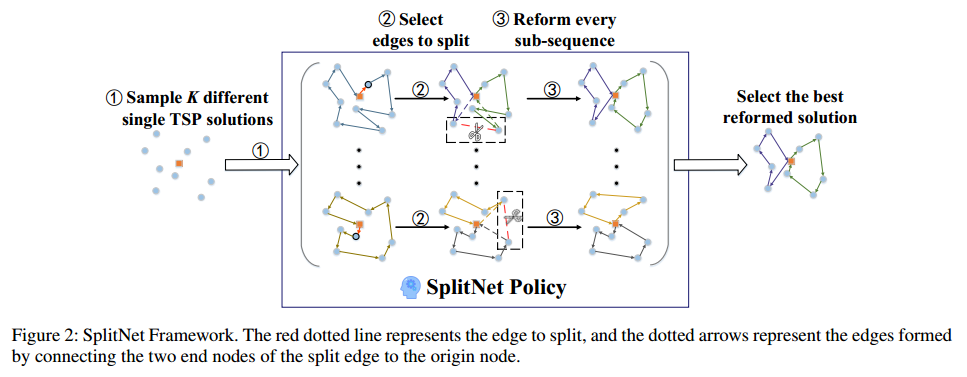
生成单个TSP解序列

只用单个最优的TSP解不能保证经过拆分和重整后能得到MinMax mTSP的最优解，所以对多个不同的单TSP解进行采样。

对于给定的实例，首先找到距离源节点最近的 $k$ 个节点，将这些节点指定为车辆离开源节点后首先访问的节点。在此基础上，用LKH3生成了 $k$ 个不同的单TSP解序列。

拆分单TSP解序列

穷举法的复杂度 $O(N^{m-1})$，即进行 $m-1$ 次拆分。为此，将选择和分割边的操作建立为MDP，并用AM模型实例化，并用RL进行训练。在训练过程中跟踪所得的策略，并将 $\pi_b$ 表示为在不同的时间不长的所有策略在验证集中获得的 rollout baseline 策略。

MDP

• state：解序列中每条边的静态和动态特征。边的静态特征包括边的长度和边的两个端点节点到原点节点的距离。动态特征包括哪些边可以分割、剩余时间步数以及所有已获得的子序列中最长子序列的长度。

• action：拆分动作是从解序列中选择一条边，将这条边拆分，将两个端点节点与原点节点连接。在实践中，强迫智能体按顺序分割，以便训练过程更快更稳定。

• reward：直观地考虑为将最长的序列的长度的负数作为奖励。考虑到奖励的大小不应该取决于问题规模的大小，也不取决于单个TSP解决方案的质量，而应该取决于与baseline之间的差距。因此奖励设置为

  \[r_t=\left\{\begin{array}{r} 0, t \neq T \\ -\frac{\mathcal{L}(\pi)-\mathcal{L}\left(\pi_b\right)}{\mathcal{L}\left(\pi_b\right)}, t=T \end{array}\right.\]

  该奖励函数有利于减少方差和加速RL的收敛速度。这个奖励函数是稀疏的。

SplitNet策略网络的模型

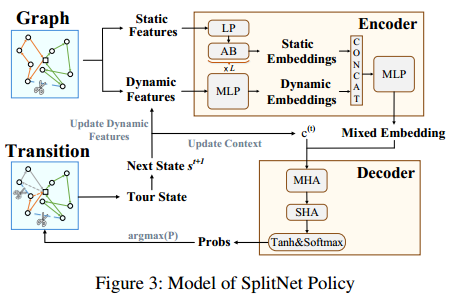
编码器的输入是每条边的静态和动态特征，输出是每条边的嵌入。通过线性层（LP）和注意力块（AB）对静态边缘特征进行处理。静态特征值计算一次。动态信息用MLP来提取。将动态信息和静态信息合并，得到各条边的混合嵌入。静态边嵌入中还引入了位置编码，以感知输入的序列化特征。

解码器的输入 $[h_{graph},h_{last}]$。$h_{graph}$ 是所有边嵌入的平均池化，$h_{last}$ 是上一条选择的边。将其作为query输入多头注意力网络MHA中，所有的边嵌入经过一个MLP作为key和value。MHA的输出作为query输入到单头注意力SHA中，并根据所有边的混合嵌入计算key。SHA输出 $N$ 个值，通过 tanh 将这些数限制到 $[-10,10]$，并采用 mask 机制。最后用 softmax 层获得选择分割的每条边的概率。（标准的AM模型的解码器结构，写的很简洁）

决策域

上述做法从小规模上训练得到的模型泛化到大规模问题上效果很差。这一现象是由于大规模问题的策略动作空间与小规模问题下有着很大的差异。一种解决方案是限制策略在每个时间步可以分割的边的范围，使其在不同规模的问题上的动作空间趋于相似，从而提高泛化能力。

理想情况下，每个子序列的长度与整个TSP序列的理想比例应该相同。为此，可以使用以下公式来近似求得通过分裂得到的新子序列的长度与第 $i$ 次分裂操作后剩余序列的长度的理想比值：

其中，$S_0$ 是单个TSP实例的总厂，$\bar{l}$ 是所有节点到原始节点的平均距离。

在第 $i$ 次分割的时候，对于所有剩余的 $N-i$ 条边，分别计算通过分割每条边获得的新的子序列的长度与分割操作后剩余序列长度的长度之比。找到其对应的比值最接近理想比值的边，称其为核心边。但直接分割核心边可能会产生次优解，为此，定义了核心边的邻域，并让策略网络在该邻域中学习选择边。将该核心边的邻域成为决策域，即在一定规则简化下的动作选择空间。

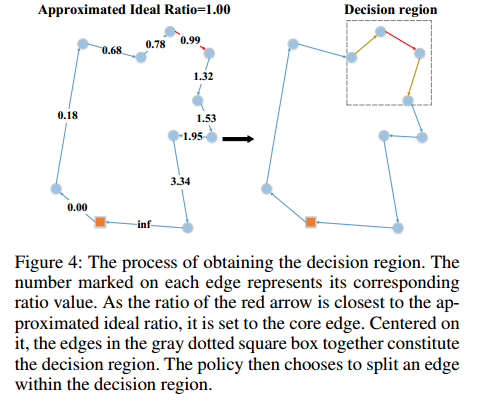
通过实验验证了加上该限制后对找到最优解的负面影响较小。

训练

Reinforce方法。但奖励函数经过归一化。即

重构操作

每次拆分后得到一个子序列，将这个子序列作为初始解提供给LKH3进行进一步优化。考虑到实例已经相对均匀地分割为 $m$ 个部分，每个子问题的大小相对较小。因此，重构只需要很短的时间。

实验

训练集随机生成，节点坐标 $[0,1]^2$​，分布随机均匀，节点数量30到100。

训练集大小30720，初始单TSP解数量25个，车辆数量在每个epoch随机独立生成，范围3到15。训练了80个epoch，每个epoch的梯度步长为1920，batch size为400。推理时采用大小为64的beam search。

验证集节点数量30到1000（每个规模数据集大小100），以及mTSPLib。

训练环境单卡A100。

在小规模CVRP上做了实验，比OR-tools和基于构造学习方法要更好。

Baselines

LKH3、OR-tools

基于学习的方法：GNN-DisPN和DAN（介绍中提到的两个方法）、改造了最现金的基于学习的方法L2D（Learn to delegate）用于解MinSum CVRP的问题。

在标准数据集上，OR-tools、DAN的结果是直接用论文中的结果。

随机数据集结果

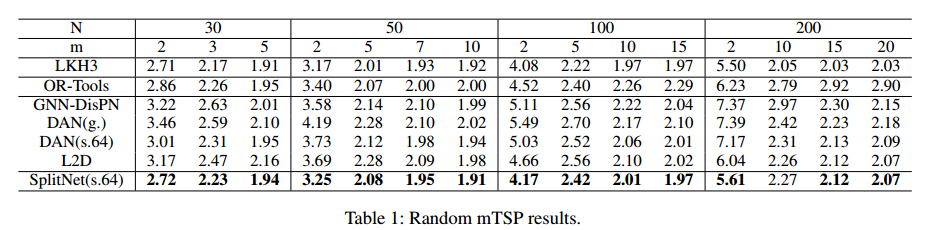
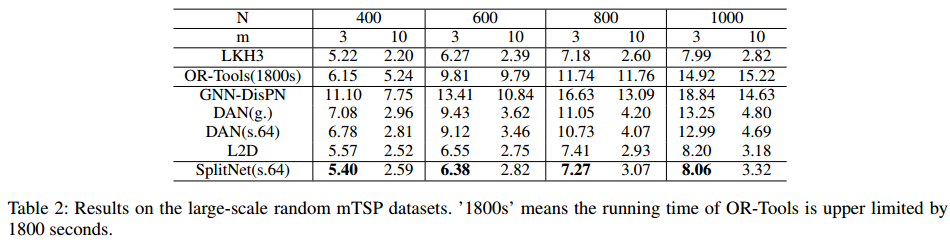
比OR-tools和目前基于学习的方法要好，大规模上更明显，但不如LKH3。

计算时间也更为优秀：

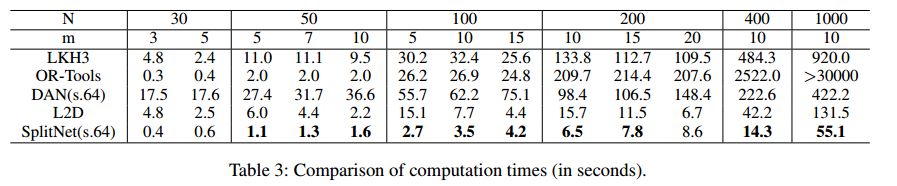
Benchmarks的结果

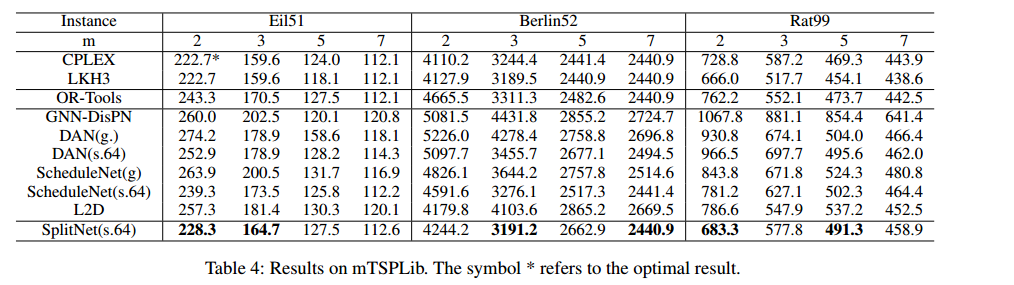
CPLEX不如LKH3的原因是，CPLEX的解是最优解的上界，而LKH3往往能找到最优解。

大多数情况更好。

消融实验

生成单一TSP解序列的有效性

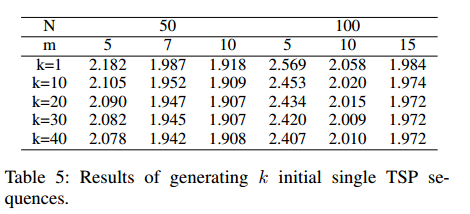
初始解采样越多，结果越好，但代价是算法的性能和计算时间，为了平衡，实验中取的30。

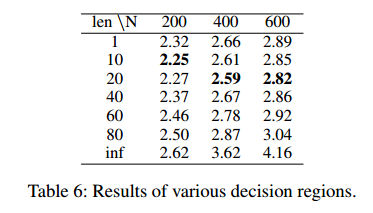
决策域带来的改进

不使用决策域（len=inf） 以及 使用核心边作（len=1）为动作。

在10到80上训练，在200/400/600上实验（没说m是多少）。

结果表明，用了更好，用len=1都比不用好（说明模型本身的泛化能力很差）。

子序列改进的好处

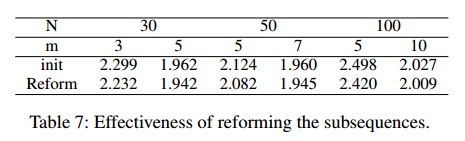
（不用跑不过OR-tools）

总结

未来工作：用SplitNet适应更复杂的领域。

（奖励函数可能可以参考，整体上看，对模型起作用的是制定的那个决策域和改进时候的LKH3重新搜索）

• Previous
  Looking Ahead to Avoid Being Late Solving Hard-Constrained Traveling Salesman Problem
• Next
  Compositional Messagepassing Neural Network (CMPNN)