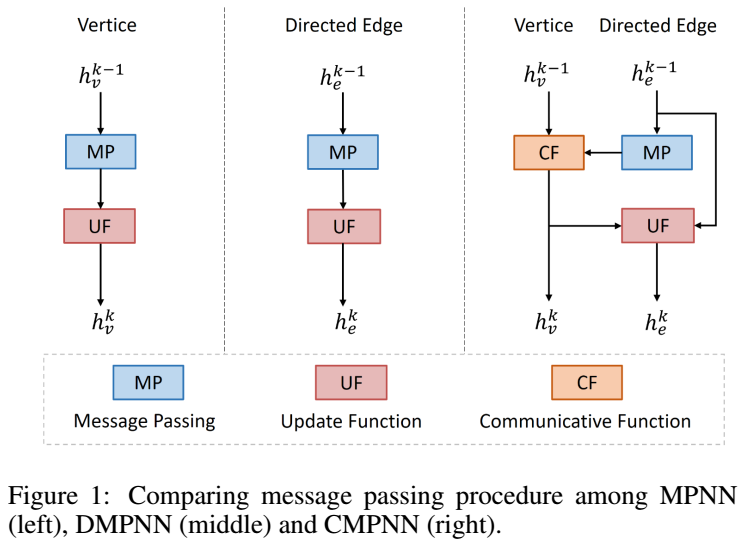
Compositional Messagepassing Neural Network (CMPNN)
选自:
- Communicative Representation Learning on Attributed Molecular Graphs(IJCAI20)
- A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs(KBS20)
图神经网络根据图的结构,通过相邻连接节点传递的消息,为每个节点 $v\in V$ 计算一个 p 维特征嵌入 $f_v$。更具体地说,CMPNN是消息传递神经网络(MPNN)的改进版本,它从以前的图嵌入技术中抽象出一个通用框架。MPNN框架包括消息生成、消息收集、消息传递和图嵌入四个步骤:
\[\begin{array}{lrl} m_{u v}=M\left(f_u, f_v, e_{u v}\right) ; & l_u=\Phi_{v \in \mathcal{N}_u}\left(m_{u v}\right) \\ f_u^{t+1}=\Psi\left(f_u^t, l_u\right) ; & g_f^t=\Phi_{u \in V}^{\prime}\left(f_u^t\right) \end{array}\]其中,$\mathcal{N}_u$ 表示节点 $u$ 的所有邻居,$M$ 和 $\Psi$ 是神经网络参数化的函数。$\Phi$ 和 $\Phi’$ 可以看作是激活函数。CMPNN使用神经网络来预测边的类型作为注意力向量。然后通过引入全局不变kernel $k\in\mathbb{R}^{t_e\times d_{in}\times d_{out}}$ , CMPNN在每次迭代时可表示为
\[f_u^{t+1}=\Phi_{v \in N(u)} h_e\left(e_{u v}\right) \mathbf{k} f_v^t\]其表示节点嵌入是基于图结构更新的。多轮更新将把消息传递得更远。最后,如果图神经网络在 $T$ 次迭代后终止,则嵌入 $f_u^T$ 的每个节点将包含来自其 T-hop 邻域的信息。
利用CMPNN的框架讨论图神经网络的参数化问题。特别地,将实验中节点嵌入的更新过程设计为:
\[f_u^{t+1}=\operatorname{relu}\left\{\max _{v \in \mathcal{N}(u)}\left[\theta_e e_{u v}\left(\theta_1 f_u^t+\theta_2 f_v^t-\theta_2 f_u^t\right)\right]\right\}\]其中,$\theta_e$、$\theta_1$ 和 $\theta_2$ 为模型参数,$\theta_e$ 为所有边的共享参数,$\theta_1$ 和 $\theta_2$ 为所有节点的共享参数,relu 为修正后的线性单位 $relu(z) = \max(0, z)$ 应用到输出。邻域最大值是聚合邻域信息的一种方法。一旦每个节点的嵌入计算完成 T 次迭代,就可以使用嵌入的节点特征和图特征(从节点特征池化)来定义分布式策略网络。