H-TSP Hierarchically Solving the Large-Scale Travelling Salesman Problem
AAAI 2023
杭州电子科技大学和微软亚洲研究所
摘要
本文提出了一个基于分层强化学习的端到端学习框架,称为H-TSP,用于解决大规模旅行商问题(TSP)。该方法包含两个策略:上层策略用于将原始的规模较大的问题拆解成多个规模较小的子问题;下层策略解决每个子问题并将子方案聚合形成原始问题的解决方案。在联合训练上层和下层策略之后,本文的方法可以直接为给定的TSP实例生成解决方案,而不依赖于任何耗时的搜索过程。为了证明所提出的方法的有效性,本文已经进行了大量的实验随机生成的TSP实例与不同数量的节点。实验表明,H-TSP可以实现与SOTA搜索为基础的方法相当的结果(差距3.42%与7.32%),更重要的是,本文减少了两个数量级的时间消耗(3.32s与395.85s)。据作者所知,H-TSP是第一个端到端深度强化学习方法,可以扩展到多达10,000个节点的TSP实例。虽然与SOTA结果在解决方案质量方面仍存在差距,但作者相信H-TSP将有助于实际应用,特别是那些对时间敏感的应用,例如网约车服务。
介绍
最好的精确求解器需要 136 个CPU年才能为 85900 个城市的实例找到最优解。
启发式算法LKH3可以了处理百万个城市的TSP实例,但需要特定的手工规则,并且依赖迭代搜索,需要大量的时间。
基于学习的TSP方法在时间上更优优势。基于学习的方法分为迭代和构造,构造能够处理小规模的实例,但很难扩展到大规模。一个例外是《Generalize a Small Pre-trained Model to Arbitrarily Large TSP Instances.》,它可以在相对较短的时间内实现与 LKH3 解决方案足够接近的解决方案(差距< 5%)。然而,在后期需要蒙特卡罗树搜索过程来不断改进解,这仍然很耗时。根据的实验结果,对于一个有10,000个城市的TSP实例,大约需要11分钟才能找到与LKH3相当的解决方案。
文章提出基于分层强化学习(HTSP)的构造方法。构造分解为两个步骤:
- 从所有要访问的剩余城市中选择相对较小的城市子集;
- 求解了一个只包含选定城市的小开环 TSP 实例;
相应地,为这两个步骤设计了两个策略:
- 选择要遍历的候选城市
- 决定这些城市的访问顺序。
使用强化学习算法对这两个策略进行联合训练,从而得到求解TSP的端到端算法。H-TSP 以分治的方式解决TSP,因此可以轻松扩展到大规模的TSP。
贡献:
- 提出 H-TSP 分层框架,是第一个可以扩展到 10000 个节点的 TSP 端到端方法。
- 大量实验:求解 10000 个节点进需要不到 4s,gap 仅有 7%。时间减少了两个数量级。
层次框架
文章提出了一种基于深度强化学习(DRL)的分层框架(H-TSP)来解决大规模的TSP问题。采用分治的方法,H-TSP包含两个级别的策略/模型,它们分别负责生成子问题和解决子问题。
以下是H-TSP的整个过程,从包含仓库的初始解出发,然后插入最接近它的节点作为第一个子问题的两个固定端点。上层策略负责分解原始问题并合并下层策略的子解决方案。由于分解将不可避免地降低最终解决方案的质量,为了减轻这种情况,让上层策略学习以自适应和动态的方式生成分解策略。另一方面,一旦确定了子问题,则将其作为开环TSP移交给低级别的策略来解决。然后将其解决方案传递给上层策略以合并到现有的部分路由中。

上层模型
上层模型可以学习一种自适应策略,该策略可以根据当前部分解和剩余节点的分布做出最佳决策。
- 可扩展的编码器:受3D点云投影中使用的技术的启发,提出了一个像素编码器,将图片编码为像素。
- 将二维空间离散成均匀间隔的 $H\times W$ 的网格,创建一组像素。
- 根据节点所在的网格将节点划分为不同的集群:$\left(x_a, y_a, \Delta x_g, \Delta y_g, \Delta x_c, \Delta y_c, x_{p r e}, y_{p r e}, x_{n x t}, y_{n x t}, m_{\text {select }}\right)$,其中 $(x_a,y_a)$ 是节点的绝对坐标,$(\Delta x_g, \Delta y_g), (\Delta x_c, \Delta y_c)$ 分别是网格中心和节点簇中心的相对坐标。如果节点已经被访问过,$(x_{p r e}, y_{p r e}), (x_{n x t}, y_{n x t})$ 表示他在局部路径上的邻居的坐标,否则为 0。$m_\text{select}$ 表示该节点是否被访问过。
- 对于有 $N$ 个节点的 TSP 实例,有一个 $(N,D),D=16$ 的特征,经过线性层后被编码成 $(N,C)$。根据被划分的聚类,在维度 $C$ 上使用 $\max$ 操作来获得每个网格的特征,并对空网格使用零填充。每个网格的组合形成一个伪图像,大小为 $(H\times W\times C)$,该图像用 CNN 进一步处理,得到DRL模型的整个TSP实例的嵌入向量。
- DRL模型是 actor-critic 架构,策略函数有一个策略头,状态值函数有一个值头。两个头部都由全连接层和激活函数组成。
- 子问题生成和合并
- 上层模型 $UpperModel$ 的输入是使用聚类后的图像 $G_{kNN}$ 和当前的局部解 $\tau_t$ ,输出一个坐标 $Coord_{pred}$。(个人理解,该节点为下一个子问题的中心)
- 找到最接近 $Coord_{pred}$ 的未访问过的节点 $v_c$,并找到最接近 $v_c$ 的已经访问过的节点 $v_b$。
- 将 $v_b$ 加入队列,开始进行宽度优先搜索,每次从队列中找一个点将其所在聚类中的所有未访问过的节点加入队列,直到找到超过 $maxNUM$ 个未访问节点。
- 由于 BFS 找到节点数量可能大于定义的子问题规模 $subLength$,所以在其中找到一个以 $v_b$ 为中心的子问题序列,使得子问题的长度不大于 $subLength$。
- 将现有的部分路由打破,得到一条有两个端点的路径,而将子问题作为开环TSP解决后,将得到另一条有两个端点的路径。
- (SelectFragment 和 SetEndpoints 都没有展开讲一笔带过,不知道怎么处理的)

- MDP(我觉得MDP好像也没有讲清楚)
- 状态:图 $G$ 的局部路径 $\tau$
- 动作:平面上的一个坐标
- 转移:$S\times A\rightarrow A$
- 奖励:执行动作前后的状态的目标函数值之差
- 折扣因子
下层模型
训练下层模型求解由上层模型生成的端点固定的开环TSP。
- 神经网络:AM模型+POMO
- 编码器输入的上下文信息 $q_{contest}=q_{graph}+q_{first}+q_{last}+q_{source}+q_{target}$,分别表示当前局部解整个图、第一个节点、最后一个节点、开环TSP的两个端点的特征。
- POMO利用了TSP的对称性,但开环TSP没有。实现对称性:在节点选择过程中,除端点之外的所有节点都将被视为TSP,没有任何约束。只要选择了一个端点,我们就让另一个端点自动被选择。通过去除两个端点之间的冗余边,得到原点开环TSP的最终解。(没看懂)
- MDP
- 状态:上述的编码器输入
- 动作:动作包含TSP中的所有节点,并使用动态掩码删除已访问的节点
- 奖励:当遇到与可行解决方案相对应的状态时,奖励等于一条路线的负成本;否则奖励为0
(感觉可能是由于篇幅限制,很多细节没讲清楚)
训练
两层模型是用DRL联合训练的。
-
上层模型用PPO训练。
- 上层模型用REINFORCE训练。
- 联合训练:将使用当前的低级策略收集轨迹来训练高级模型,同时存储由低级策略生成的子问题来训练低级模型。通过这种交错训练过程,两个层次的策略可以得到彼此的即时反馈,从而使合作策略的学习成为可能。
- 低级策略的解决方案质量对最终解决方案有重大影响。如果从一个随机的低层策略开始,高层策略将会收到很多误导性的反馈,使得它的训练很难收敛。为了缓解这一问题,通过使用从原始TSP随机生成的子问题对低级模型进行预训练,为低级模型引入了一个热身阶段。
实验
随机数据集 Random1000、Random2000、Random5000、Random10000。数据集大小除了Random1000有128个,其余都是16个。
实验设备:V100(16GB)。
参数:
- 上层模型像素编码器中的3层CNN分别有16 32 32个通道,输出维度128。
- 上层模型actor和critic网络都是一个4层的MLP。
- 下层模型有12层的自注意编码器和2层上下文注意力解码器。
- 网络的维度均为128。
- 学习率 1e-4,权值衰减为 1e-6 的 AdamW 优化器。
- kNN 的 k 设置为40,子问题长度 $subLength$ 设置为 200,子问题最大新节点数 $maxNum$ 设置为 190。
- 下层模型在热身阶段训练 500 轮,联合训练对不同规模训练 500 1000 1500 2000 轮。
Baseline:
- Concord求解器
- LKH3
- OR-Tools
- POMO
- DRL-2opt(基于搜索的DRL)
- Att-GCN+MCTS(一种将GCN模型训练与监督学习和MCTS搜索来解决大规模TSP的方法)
实验结果
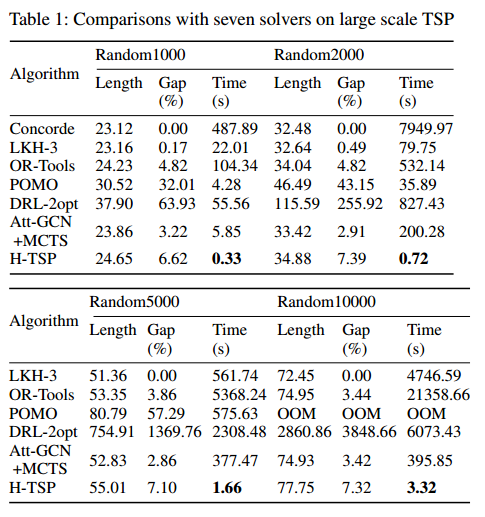
POMO和DRL-2opt很差是因为他们不能直接在大规模问题上训练。
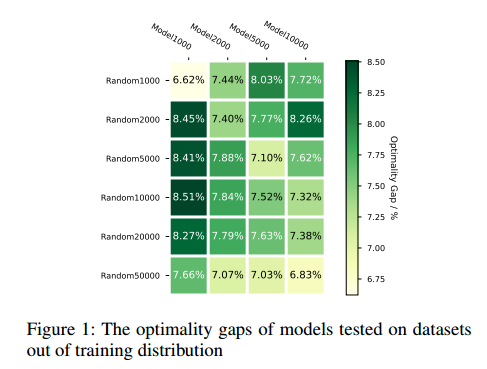
泛化能力:x轴是训练模型,y轴是泛化的问题规模。
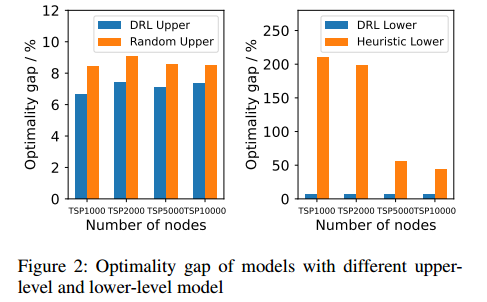
消融实验
上层模型用随机坐标替换,下层模型用最远插入(1974年)的启发式方法替换,在四个数据集中评估。
下层模型替换成LKH3和Att-GCN+MTCS:
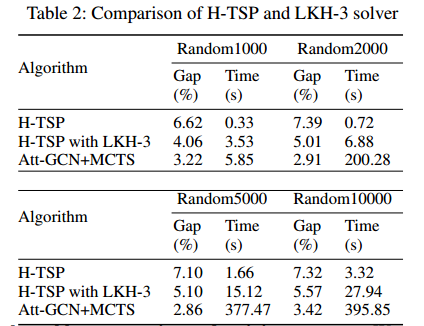
效果更好但时间更长,这表明下层模型可以使用DRL加速训练。
文中提到的四种技术的消融:
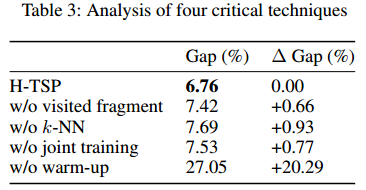
该部分使用1000个节点的TSP训练了250轮,并在1000的问题上进行测试。
总结
提出以分治为主要思想的H-TSP框架,使用LKH3作为下层模型可以进一步提高模型的性能。
未来工作:扩展到其他大规模问题。