Deep reinforcement learning for the dynamic and uncertain vehicle routing problem
2023 Applied Intelligence
福州大学经济与管理学院
摘要
对现实城市物流进行准确、实时的跟踪已成为智能交通领域的热门研究课题。而城市物流服务的路径选择通常是通过复杂的数学和分析方法来完成的。然而,现实城市物流的性质和范围都是高度动态的,现有的优化技术无法精确地表述路线的动态特性。为了确保客户的需求得到满足,规划人员需要对这些变化迅速做出反应(有时是即时的)。本文提出了一种新的深度强化学习框架来解决动态不确定车辆路径问题(DU-VRP),其目标是在动态环境中满足不确定的客户服务需求。考虑到该问题中客户需求信息的不确定性,设计了局部观察马尔可夫决策过程,在具有动态关注机制的深度神经网络实时决策支持系统中频繁观察客户需求的变化。此外,提出了一种前沿的强化学习算法来控制DU-VRP的值函数,以更好地训练路由过程的动态性和不确定性。在不同数据源下进行了计算实验,得到了满意的DU-VRP解。
介绍
VRP两个扩展:
- 动态VRP (Dynamic VRP, DVRP),它与基本VRP的不同之处在于,它假设与客户、地点和车辆相关的一些值可能会动态变化。这样的主张在当今充满活力的生产和运输环境中很常见。
- 动态不确定VRP (Dynamic and ununcertainty VRP, DU-VRP),它是DVRP的扩展,在车辆路径过程中同时考虑了不确定性和动态性。在实践中,很难事先知道准确和完全确认的信息。例如,调度员必须更新有关车辆位置的实时信息,并考虑每个客户需求的不确定性。
在本研究中,主要关注DU-VRP,因为它具有更广泛的适用性。
我们考虑通过深度强化学习(DRL)方法来解决DU-VRP。图1所示的小型DU-VRP示例揭示了需求不确定性如何以一致的方式影响车辆路线,并表明了在DU-VRP环境下实时通信的重要性。实时通信需要采集不确定信息,动态分配任务。在DU-VRP中,新客户动态到达服务区域。图1显示了不确定动态环境下单个车辆的路线执行情况。初始路线打算在车辆于 $t_0$ 离开仓库之前访问当前已知的客户(即节点A、B、C、D、E)。当车辆执行这条路线时,来自客户的一些请求(即节点L、X、Y、Z、K)可能依次出现在 $t_1$、$t_2$、$t_3$ 时刻。每个顾客都有自己的特定需求。此外,消费者的需求可能是不确定的和动态变化的,由他们的需求产生的请求是高度不确定的。在这种情况下,该初始路由可能会根据环境的变化进行调整,例如,在 $t_f$ 时刻执行的路由可能会更改为 A→L→B→X→C→Y→D→Z→E→K。
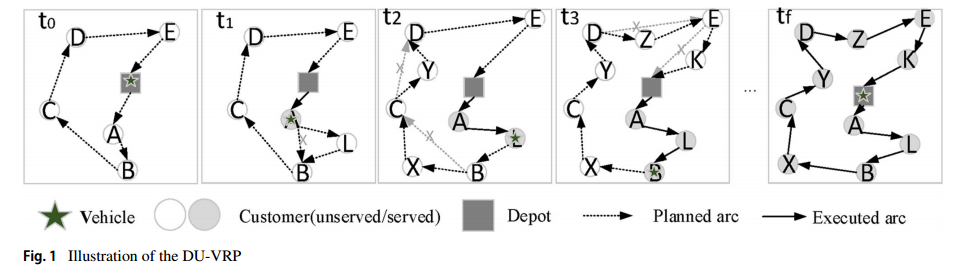
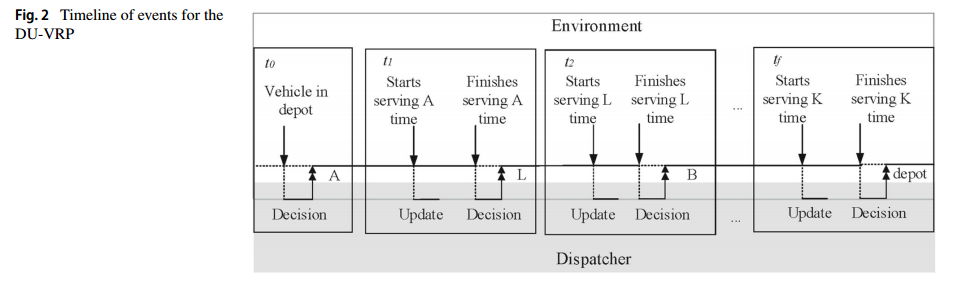
图2描述了DU-VRP环境下的实时通信方案。调度程序可以在每个时间步调整路由以适应动态环境。在动态DU-VRP环境中,调度员被视为向车辆发出指令的代理。当车辆准备就绪时,调度员做出顺序决策,以满足每个客户的需求(例如,图2中第一个双头箭头突出显示的客户a)。当客户的位置导致环境变化时,DU-VRP系统实时接收环境信息,并做出更新新路线的潜在决策。
挑战:
- 使调度员能够实时地从客户-车辆数据中学习。消费者的需求可能是不确定的和动态变化的,由他们的需求产生的请求是高度不确定的。每个基于客户车辆的时间都与高维数据相关联,以解决动态约束。
部分可观察马尔可夫决策过程(部分可观察马尔可夫决策过程,POMDP)是改进的马尔可夫决策过程,其中每个时间步长的状态是不可知的,具有不可预测性,即状态不是完全可观察的。基于图的POMDP是标准POMDP的扩展,它将路由和图信息添加到状态空间、动作空间和奖励结构中。
贡献:
-
首批研究如何为DU-VRP开发一种新颖的端到端DRL框架的研究之一。
-
设计了一种新颖的基于图形的POMDP模型来反映DU-VRP中的动态环境和不确定的客户需求。
-
设计了一种自适应策略来训练目标函数值并提高学习性能,特别是对于基于图的POMDP模型。
-
提出的DRL方法通过基线比较和使用真实世界数据的敏感性分析进行验证。
相关工作
一些比较古老的技术,略。
本文从两个方面研究了基于DRL的按需拼车问题:
- 匹配乘客需求和可用车辆的订单调度;
- 车辆重新定位是一种通过将闲置车辆从一个区域移动到另一个区域来平衡车辆供需的主动方法。
一系列冗长的枚举,介绍DRL解决各种具体问题的方法,总结如下表。
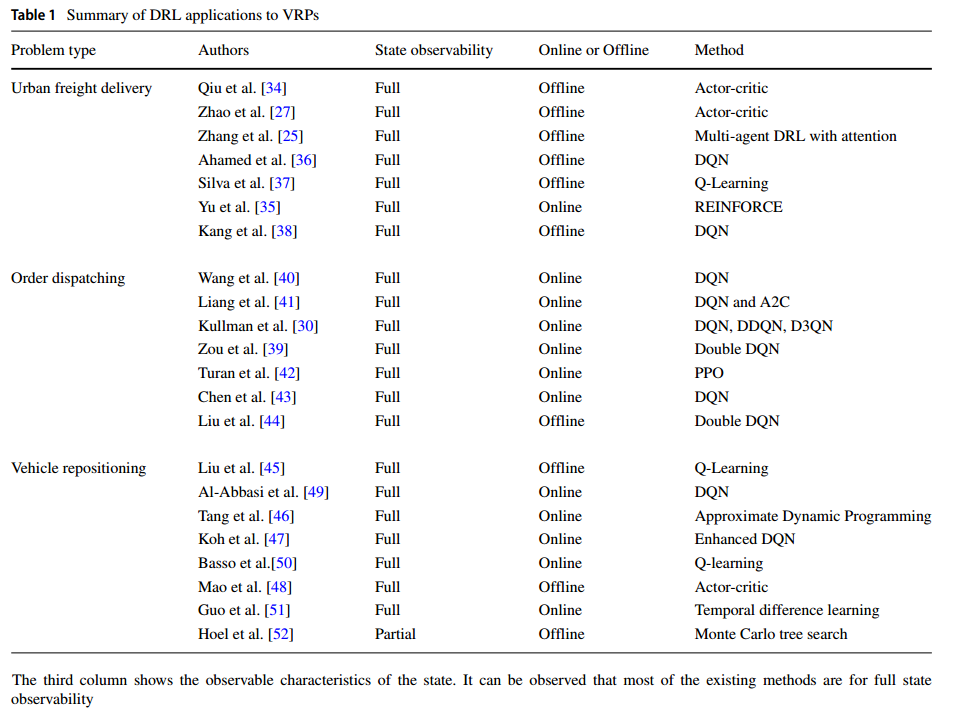
这些现有的工作并没有随着时间的推移而优化,也没有通过捕捉客户需求的动态方面来面对不确定性。
- 迄今为止,关于应用DRL (RL)处理VRP系统中的动态和不确定性问题的学术论文还很少。据我们所知,这项研究开创性地探索了如何为DU-VRP开发一种新的DRL方法。
- 在文献中,大多数DRL (DL)方法都是基于全状态可观察性。相反,我们采用一种新的基于图的部分可观察马尔可夫决策过程(POMDP)来表述DU-VRP系统中不确定性和动态的部分状态可观察性。
- 大多数现有研究应用单个神经网络(例如,NN, RNN等)来近似其端到端DRL框架中的值函数。相比之下,我们提出了一种尖端的图嵌入网络来处理DU-VRP环境下的动态客户坐标。
DRL for DU-VRP
Modelling the DU-VRP by POMDP
实际应用程序通常是在动态环境中生成的。由于客户需求的时间依赖性,DU-VRP情况不一定具有马尔可夫性质。
这种实现的问题是在优化总旅行成本的同时响应新的需求。由于不确定性和动态性的困难,静态混合整数规划(MIP)模型不能直接用于DU-VRP的建模。基于图的POMDP是标准POMDP的扩展,它将路由和图信息添加到状态空间、动作空间和奖励结构中。
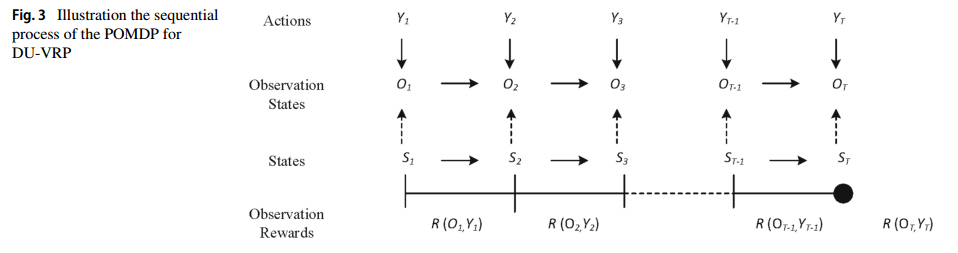
作为对文献的贡献,我们提出了一种新的基于图的部分观察马尔可夫决策过程(POMDP)来建模DU-VRP。图3演示了POMDP通过以下定义的符号对DU-VRP建模的顺序过程。
-
Time steps:$t=0,1,\cdots,T$
-
States
- 基于图的POMDP与有向图模型 $G=(\mathbb{C},E)$,其中 $\mathbb{C}=\lbrace c_0,c_1,\cdots, c_n,c_{n+1}\rbrace$ 表示节点集合,$c_0,c_{n+1}$ 表示仓库源点和仓库汇点。$E$ 是边集。
- 车辆集合 $k=1,\cdots,m$,每辆车从 $c_0$ 出发到 $c_{n+1}$ 结束
- 每个客户节点有一个需求 $d_i$
- 定义二元变量 $u_{i,k}$ 表示结果中 $k$ 服务 $i$,二元变量 $x_{ijk}$ 表示 $k$ 经过了 $(i,j)$
- 状态 $\mathcal{S}=\lbrace S_t,t=1,\cdots,T\rbrace$,每个 $S_t$ 包含三个元素:
- 一组处于当前状态客户节点集合 $\mathbb{C}_t$,由两部分组成:$\mathbb{C}_t^{next}$ 表示未服务客户,$\mathbb{C}_t^{new}$ 表示当前时刻的新客户
- 当前车辆的位置 $\mathcal{M}_t$;
- 客户在当前时刻的需求 $\mathcal{D}_t$,由新客户服务过程中动态获得
-
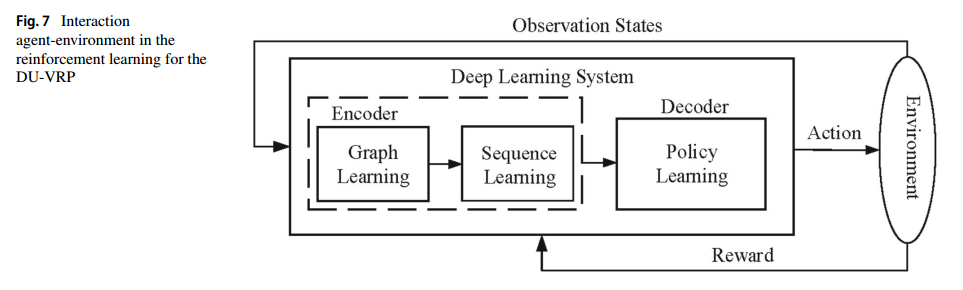
Observation states:DU-VRP决策在真实地图中动态执行,智能体必须根据一组观察结果推断出一组可能状态的概率分布。
The DU-VRP decisions are dynamically executed in a real map, in which the demand of customers is inaccessible for the agents indeed. As a result, the agent has to infer a probability distribution over the set of possible states based on a set of observations. The observation states are associated with an observed current customers’ location $\tilde{\mathcal{M}}_t$ and observed customers’ demands $\tilde{\mathcal{D}}_t$ at time step $t$, defined as $O_t=\left\lbrace\left(\tilde{\mathcal{M}}_t, \tilde{\mathcal{D}}_t\right) \mid\right.\tilde{\mathcal{M}}_t=\left\lbrace\tilde{m}_{i k}^t, i, k=1, \ldots, n\right\rbrace, \tilde{\mathcal{D}}_t=\left\lbrace\tilde{d}_i^t, i=1, \ldots, n\right\rbrace$ where $\tilde{m}_{i k}^t$ is the observed distance between new customer $i$ and vehicle $k$ at time step $t$, and $\tilde{d}_i^t$ is the observed demand of customer $i$ at time step $t$. Thus, the whole observation space is defined as $\mathcal{O}=\left\lbrace O_t, t=\right.$ $1, \ldots, T\rbrace$
- Action:$Y_{t+1}$被定义为一个指针,指向可用客户的动作。动作顺序记为$Y = \lbrace Y_1\cdots, Y_t\rbrace$ 记录动作的过去信息。
- 状态转移 $\mathbb{T(s’\mid s,y)}$
- 观察转移概率 $p(o’\mid s,y)$
- 观察奖励函数:奖励函数定义为 $R\left(O_{t+1}, Y_{t+1}\right)=V\left(O_{t+1}, Y_{t+1}\right)-P\left(O_{t+1}, Y_{t+1}\right)$
- $V$ 是完全观察奖励函数,$\left(O_{t+1}, Y_{t+1}\right)=\sum_{k=1}^m \sum_{i=1}^n u_{i k}-\sum_{k=1}^m \sum_{i=1}^n \sum_{j=1}^n c_{i j} x_{i j k}$,作为满足需求的奖励和行动中两个顾客之间的距离的负值来计算的(前面那部分的意义是什么,鼓励服务更多的用户吗)
- $P$ 是部分观察惩罚函数,$P\left(O_{t+1}, Y_{t+1}\right)=C_1 \sum_{k=1}^m\max \left\lbrace\sum_{i=1}^n d_i \sum_{j=1}^n x_{i j k}-q_k, 0\right\rbrace$,其中,$q_k$ 和 $d_i$ 分别表示车辆 $k$ 的容量和客户 $i$ 的需求。在这个惩罚函数中,系数为 $C_1$ 的惩罚项保证了每辆车的容量约束。即时奖励 $R_t$ 是在车辆采取行动 $y_{t+1}$ 从 $O_t$ 移动到 $O_{t+1}$ 后产生的。
- 策略:$\pi$,控制在每个时间步处理所有客户请求的行程。
- 状态价值函数:$V_\pi(o)=\mathbb{E}_\pi [\sum_{k=0}^{\infty} R_{t+k+1} \mid O_t=o]$,它是在状态 $o$ 开始执行策略 $\pi$ 时的期望收益。
- 动作价值函数:$\mathbb{Q}(o, y)=\mathbb{E}\left[R_{t+1}+\right. \left.v\left(O_{t+1}\right) \mid O_t=o, Y_t=y\right]$,在状态 $o$ 下采取动作 $y$ 的期望收益
DRL 方法
主要结构如下:
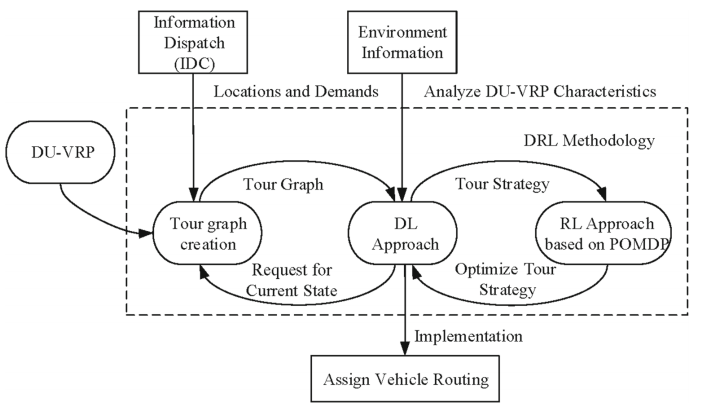
在每个时隙的开始,调度员接收来自IDC (information dispatch center)的数据,IDC实时收集当前客户需求。IDC的主要功能是根据动态环境的变化,对位置和需求的整体信息流进行更新。环境信息可以通过深度学习方法将一组观测值添加到POMDP模型中,深度学习方法旨在获取观测值。然后,智能体观察每个状态下的环境,并通过编码器-解码器网络产生一个动作。最后,采用RL方法实现优化的行程策略。
DL方法在接收到客户需求的实时信息时,通过创建tour图的图形来制定tour策略,然后将tour策略传递给RL方法。随后,RL方法优化每辆车的tour策略,使每辆车都实现其tour策略,驶向下一个节点。此外,DL方法将对当前状态的请求传输给带有更新数据的POMDP模型。
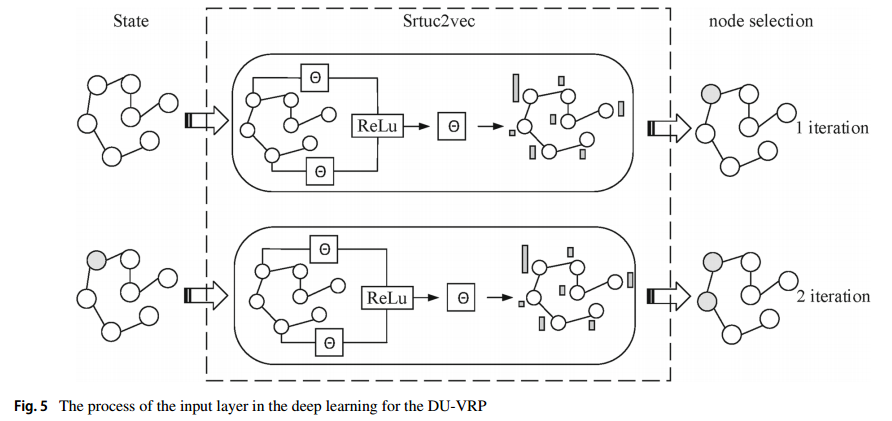
首先用 Sturc2vec (2017 KDD)将每个节点编码为向量,Sturc2vec 是针对图相似性提出的一种图 embedding。整体的细节如下
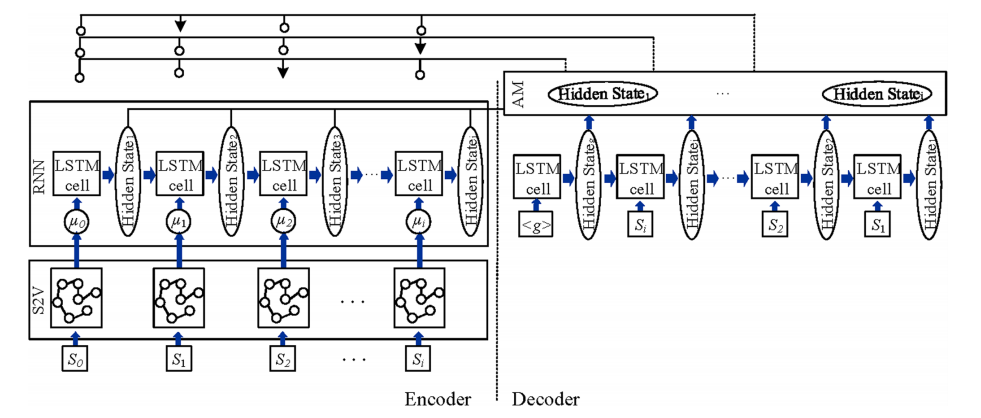
具体来说,对于时刻 $t$ 的每个节点 $c_i$,通过 S2V 网络计算成 $p$ 维的向量,比如 $\mu_i^t$。S2V网络初始化所有嵌入 $\mu_i^0$,所有嵌入在每次迭代时同步更新,
\[\mu_i^{t+1} \leftarrow f\left(c_i,\left\{\mu_j^t\right\}_{j \in \mathcal{N}(i)},\left\{\tilde{m}_{i j}^t\right\}_{j \in \mathcal{N}(i)}, \tilde{d}_i^t ; \Theta\right)\]其中,$\mathcal{N}(i)$ 是 $c_i$ 的邻居集合,$\tilde{m}_{i j}^t$ 是 $i,j$ 间的观察距离,$\tilde{d}_i^t$ 是观察需求,$f$ 是一个非线性函数。其中 $f$ 定义为
\[\begin{aligned} &\begin{aligned} \mu_i^{t+1} \leftarrow & \operatorname{ReLU}\left(\theta_1 c_i+\theta_2 \sum_{j \in \mathcal{N}(i)} \mu_j^t+\theta_3 \sum_{j \in \mathcal{N}(i)} \operatorname{ReLU}\left(\theta_4 \tilde{d}_i^t\right)\right. \\ & \left.+\theta_5 \sum_{j \in \mathcal{N}(i)} \operatorname{ReLU}\left(\theta_6 \tilde{m}_{i j}^t\right)\right) \end{aligned}\\ \end{aligned}\]然后就输入到 LSTM 当中(公式就不列出来了)。
为了从编码上下文预测客户之间的分布,改进了注意机制(AM)方法。传统的 AM 编码器部分只包含当前迭代的坐标和需求信息,解码器部分只记住过去的静态信息。本文设计了一个带有池化层的注意机制来修改解码器网络的输入。所有隐藏状态 $C^i_t$ 由编码器中每次迭代的静态(状态信息)和动态(观测状态信息)元素 $C^e_i\in\mathbb{R}$ 组成。$C^i_t$ 很重要,因为它是编码器和解码器输出的组合,包含有关客户需求的先前信息。在将隐藏状态提供给解码器之前,我们首先在隐藏状态的一个维度上应用池化层,并确保它具有相同的形状作为解码器输入。结合编码器和解码器隐藏状态 $C^d_i\in\mathbb{R}$ 确定对齐向量。(公式就不列出来了,看起来只是增加了一个池化层,以及一些上下文信息)
强化学习方法用的改进的A3C,如下两张图所示(具体改进在图8):
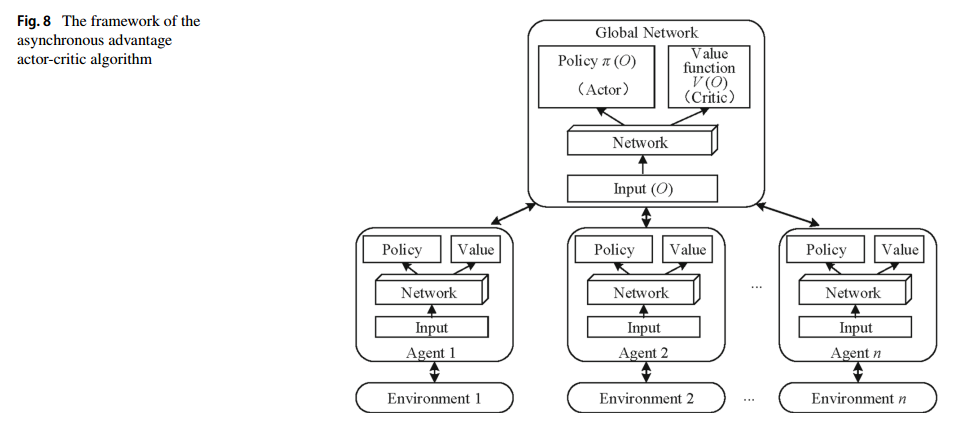
具体伪代码如下

实验和结果
参数设置
实验没用显卡。
地图是 $1\times 1$ 的,客户需求是 $[1,9]$ 的随机变量,车辆的载重是 20 到 60 不等。具体如下
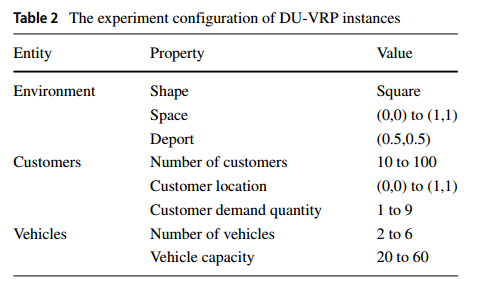
超参数如下
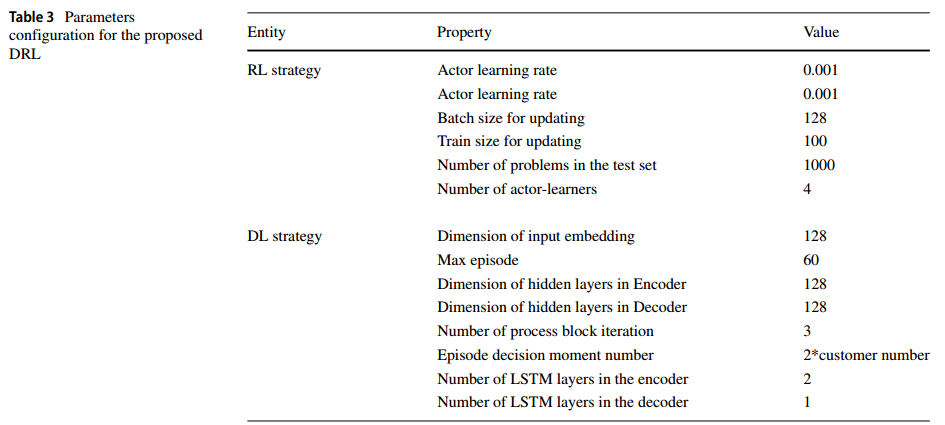
问题规模如下
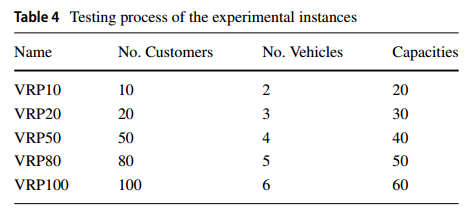
表现如下:

benchmarks 上的表现
解码用 greedy 和 sample。
benchmark:cf.https://neo.lcc.uma.es/vrp/vrp-instances/,使用了 Set-A 和 Set-B
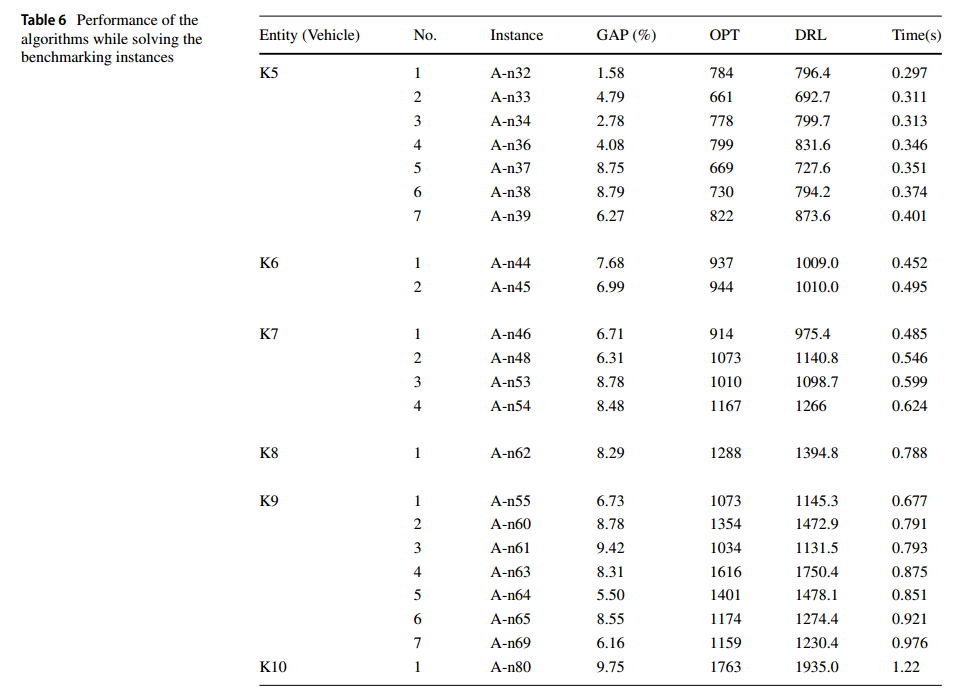
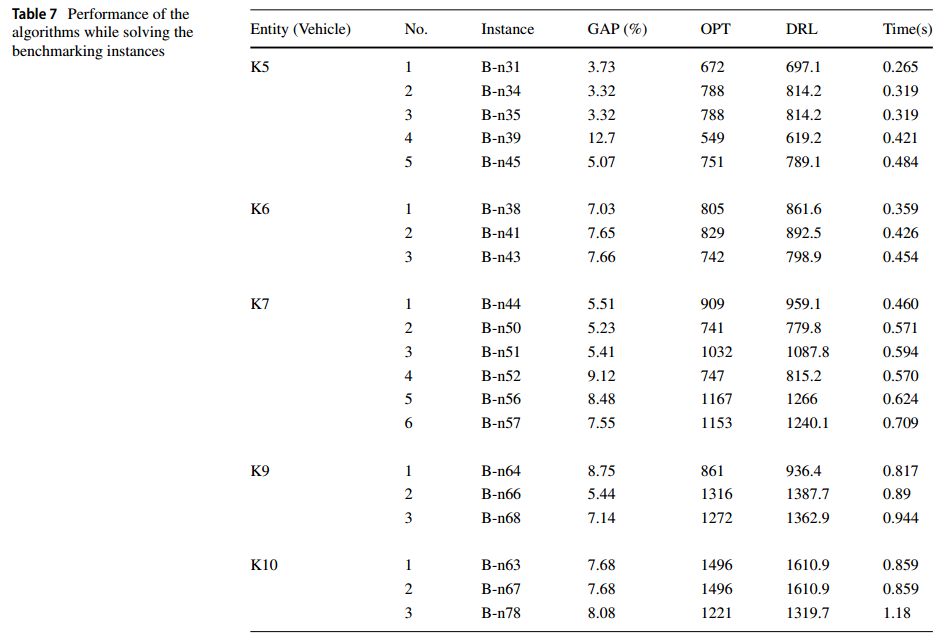
OPT 从网站获取,表列 KX 表示有X辆车,实例 A-nY 表示有Y个客户的数据。表中各列分别为:实体(Vehicles)、实体中实例数(No.)、实例名(instances)、GAP(%)、OPT和DRL得到的总行驶距离(distance)的值、计算时间(time),单位为秒。
表现如下:
(他说过没有其他算法能解)
真实世界表现
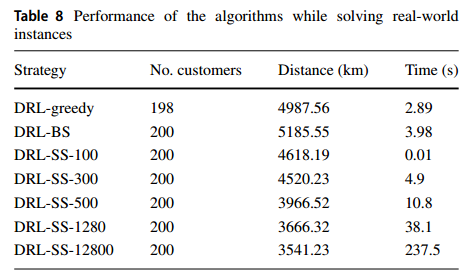
第三组实验是在一个真实世界的交通网络中进行的,使用的数据来自德国科隆(参见https://sumo.dlr.de/docs/Data/Scenarios/TAPASCologne.html)。
表现如下:
总结
未来研究:处理其他问题。