Heuristics for Vehicle Routing Problem: A Survey and Recent Advances
arxiv 2023
写开题报告的时候偶然看到的
VRP 是 20 世纪 50 年代提出的问题[1],其在现实中巨大的工业应用和经济价值吸引了很多学者,在大量学者的研究下,产生了一系列的求解算法。这些算法大体上可以分为三类:精确求解算法、启发式算法和基于机器学习的算法。
在这三类算法中,精确求解算法保证了解的最优性,并且在理论上能够解释求解方法的合理性。但是,精确求解算法往往有着指数级别的求解时间复杂度,很难有效地处理现实中大规模的车辆路径问题以及其复杂的约束。相对于精确求解算法,启发式算法计算的时间复杂度相对更加合理,并且具有良好的泛化能力,但相对地,启发式算法依赖专家知识,需要复杂的人工设计已到达良好的效果。基于机器学习的算法是一种新兴的算法,采用数据驱动的方式,利用从大量数据中学习到的知识,以端到端的方式或者迭代改进的方法快速获得可接受的解决方案。然而,它的解决方案的质量和模型的泛化性仍然是具有挑战性的课题。
精确求解算法
动态规划和分支定界等方法是精确求解算法的主要类型。动态规划将车辆路径规划问题拆分成一系列更简单的子问题后进行迭代求解,在小规模实例中表现良好。分支定界方法包括了分支定价[56]、分支剪价[57]、分支剪价定价[58]等不同的方案。[54]提出了一种分支定界算法算法来求解取货和送货车辆路径规划问题问题,算法基于三个约束:子线消除和优先约束、广义顺序约束和顺序匹配约束。[55]提出了一种新的分支剪价算法,它是一种结合了分支定界、剪切平面和列生成的方法,用于求解整数线性规划问题。分支剪价算法通过将车辆路径规划问题数学建模后,转换成整数线性规划问题,考虑列生成中的两个定价子问题来解决问题。
尽管提供了最优的解决方案,但考虑到指数级的复杂度,精确的方法对于大规模的计算来说是非常沉重的。
启发式算法
关于车辆路径规划问题的启发式研究分为三类[2]:基于构造的启发式、基于改进的启发式和元启发式。其分类如图1所示:
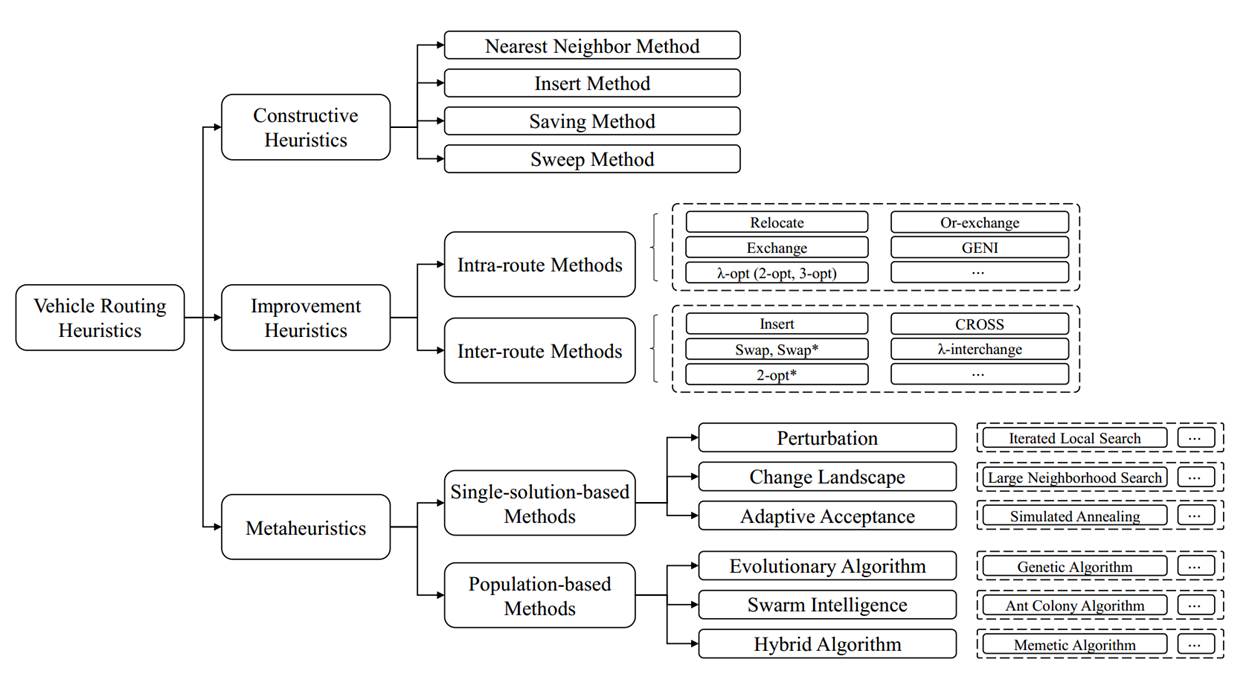
图1:车辆路径规划问题的启发式研究分类
基于构造的启发式
基于构造的启发式从空集开始按照一定的方法构造路径。该方法能够快速构建解决方案,但其结果与最优解之间通常存在一定的差距。基于构造的启发式可以归纳为四种算法框架:最近邻法、插入法、节约法、扫描法。
最近邻法通常以仓库为路径的起点,通过贪婪的思想添加最近可行的未访问的客户来扩展当前的路径。当添加剩余的任何客户都会违反约束的时候,则从仓库初始化一条新的路径。最近邻法作为一些复杂算法的组件,集成到如禁忌搜索[3]、模拟退火[4]、文化基因算法[5]、大邻域搜索[6]等算法当中。
最近邻法无法处理具有复杂约束的车辆路径规划问题,插入法在一定程度上克服了这个问题。插入法初始化一些空路由,将未访问的客户依次插入到路径中,但不一定插入到每条路径的末端。插入到路径末端可能导致路径违反约束,因此可以通过计算得到路径中可以插入的满足约束的位置。插入法可以辅助蚁群算法[7]和大邻域搜索[8]来获得高质量解。
节约法从一个初始的解决方案开始,其中不同的路线只为单个客户服务。从初始解出发,迭代地将较短的路线合并成总成本较低的较长路线。该算法具有分治的思想,能够处理较大规模的车辆路径规划问题。结合蚁群算法[9]、遗传算法[10]、蒙特卡洛方法[11]等,节约法扩展成具有更强性能的求解方法。
扫描法首先以仓库为原点,根据极坐标角度对节点进行排序。一种方案是,节点被循环地添加到路由中,如果插入不可行,将创建一条新路由。另一种方案是将所有客户根据极角聚为若干类,并在每个类中求解一个旅行商问题。扫描法能够扩展到各种具有复杂约束的车辆路径规划问题,如基于花瓣的方案[12]、结合局部搜索的扫描法[13]、结合遗传算法的扫描法[14]。
基于改进的启发式
基于改进的启发式以一个初始解出发,通过迭代以一定方法改进初始解以获得更高质量的解。目前使用最广泛的两种基于改进的启发式是路径内改进启发式和路径间改进启发式,两种方案的区别在于邻域的结构。
路径内改进启发式算法只考虑一条路径的邻域,朴素地描述为,从一条路径上一处若干条边,并以另一种方式重新连接这若干条边。图2展示了重新连接的不同方案,包括了Relocate、Exchange、2-opt、3-opt[15]、OR-exchange[16]、GENI[17]。
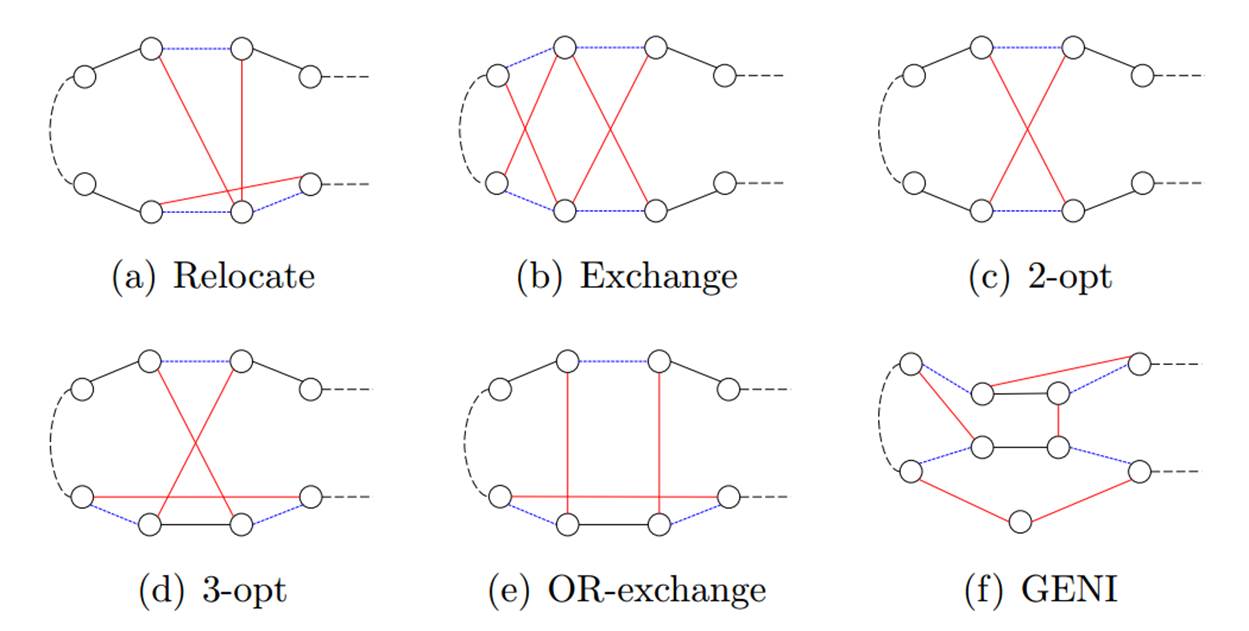
图2:路径内改进启发式的不同方案
路由间启发式涉及跨多条路由的本地搜索。其中许多是路由内对等体的扩展。例如,insert和swap分别是relocate和exchange的扩展。前者从一条路线中删除客户,并将其重新插入到另一条路线中。后者交换来自不同路线的两个客户。另外,为了区别于众所周知的2-opt,将不同路径的两条边交换记为2-opt*。CROSS交换两个字符串,每个字符串最多有λ个客户。λ-交换进一步推广了CROSS。它允许在两条路由之间交换任何小于λ的节点集,即使它们不是连续的。图3给出了一些具有代表性的路由间改进启发式算法:
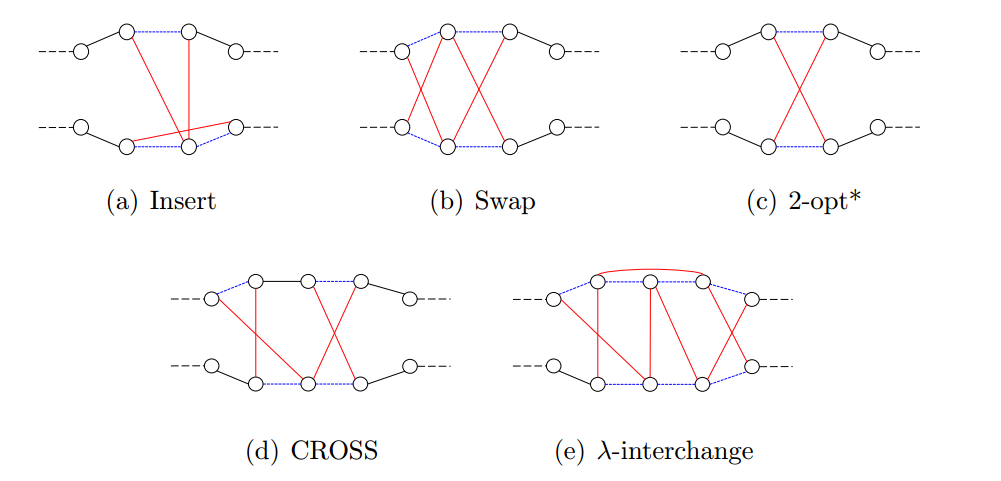
图3:路径间改进启发式的不同方案
元启发式
元启发式试图利用目标问题的特征和结构,以一种更一般的方式解决问题。从种群的角度,可以将元启发式分成两类:基于单个解的方法和基于种群的方法。
基于单个解的方法中,代表性算法为模拟退火[18]、禁忌搜索[19]、迭代局部搜索[20]、大邻域搜索[21]。这些算法衍生出来的各种变体,能够一定程度上解决一些具有复杂约束的车辆路径规划问题。具有选择邻域移动的自适应机制的模拟退火方法[22]能够处理多交叉码头异构车队的车辆路径规划问题。一种改进的基于群体的模拟退火算法[23],在优化过程中保持一个解的种群,每个解决方案都使用模拟退火启发式改进,并通过交叉算子将解决方案合并在一起,能够有效处理带有容量约束的车辆路径规划问题。基于可变邻域搜索框架的混合方法[24],在局部搜索过程中采用禁忌列表来避免循环。在变邻域搜索的震动过程中使用禁忌搜索来求解一类多车辆的车辆路径规划问题[25]。针对有容量的车辆路径规划问题,[26]开发了一种具有多样性控制方法的自适应迭代局部搜索,结果在大规模问题上很有竞争力。[48]最近设计了一种大邻域搜索算法,没有多个算子和权重自适应,它只使用相邻字符串移除和贪婪插入,分别使用闪烁表示破坏和重新创建。
基于种群的方法中,代表性算法为遗传算法[10]、蚁群算法[9]、文化基因算法[5]。由于传统的遗传搜索框架在组合优化问题并没有很好的效果,将遗传算法与不同的搜索技术相结合是一种趋势,包括集成粒子群[28]、模拟退火[29]和扫描法[30]。同样,蚁群算法也结合了其他算法,以提高在车辆路径规划问题上的性能,包括解决取货和送货车辆路径规划问题[31]、具有灵活时间窗口的多目标车辆路径规划问题[32]等。混合遗传搜索[33]是文化基因算法中具有代表性的一种,它将遗传搜索和局部搜索算子结合起来,对种群进行多样性控制。
基于机器学习的算法
用于解决车辆路径规划问题的基于机器学习的算法主要分成三类,分别为学习构造、学习搜索和学习预测。
学习构造
学习构造的方案通过迭代地向部分解中添加节点来构造解。第一个学习构造求解器是基于递归神经网络和监督学习的指针网络[35]。有学者利用图神经网络进行图嵌入[36]和更快的编码[37]。后来,注意力模型[38]在车辆路径规划问题中的出现启发了许多后续的模型,其中最引人关注的是多重优化策略优化[39],它通过不同的rollout和数据增强显着改进了注意力模型。学习构造求解器可以在几秒钟内生成高质量的解决方案。然而,即使配备了如采样[38]、波束搜索[40]等方法或其他高级策略如不变表示[41]、学习协作策略[42]等,学习构造求解器也容易陷入局部最优。最近,高效主动搜索[43]通过更新预训练的一小部分来解决这些问题。
学习搜索
学习搜索的方案以搜索的方式迭代地将一个解决方案改进为一个新的解决方案。早期的尝试[44]严重依赖于传统的本地搜索算法和较长的运行时间。神经大邻域搜索求解器[45]通过控制一个破坏和修复过程来改进[44],该过程使用手工制作的算子破坏部分原有解,然后使用深度学习模型修复被破坏的部分。最近,一些学习搜索求解器专注于控制更适合车辆路径规划问题的k-opt启发式。guide 2-opt[46]是最早尝试的神经k-opt启发式模型,其性能优于注意力模型。使用对偶联合注意力机制和循环位置编码方法代替了传统的vanilla注意力[47]能够改进[46]。进一步将对偶联合注意力机制升级为同步注意力机制[48]能够减少计算成本。然而,这些神经k-opt求解器受到较小且固定的k的限制。此外,尽管学习搜索求解器通过直接学习搜索而努力超越学习构造求解器,但即使给定较长的运行时间,它们仍然不如那些最先进的学习构造求解器。
学习预测
学习预测求解器通过预测关键信息来指导搜索。使用图神经网络来预测热图[49]是方案之一,热图表明最优解中存在某条边的概率,然后使用波束搜索来求解车辆路径规划问题。基于分而治之、热图合并和蒙特卡罗树搜索[50]的方案被用于更大规模的车辆路径规划实例。最近,DIFUSCO求解器[51]提出用扩散模型[52]取代图神经网络。与学习构造或学习搜索求解器相比,学习预测求解器在大型实例中具有更好的可扩展性。然而,由于在准备训练数据和多个车辆方面具有一定困难,学习预测求解器大多仅限于监督学习和单个车辆。虽然学习预测求解器DPDP[53]能够用动态规划方法求解带有容量约束的车辆路径规划问题,但其求解性能不如最好的学习构造求解器[43]。
洞察SOTA
洞察四个被广泛研究的车辆路径问题的最新启发式方法:有容VRP、时间窗VRP、多车场VRP和异构VRP。前沿方法的成功得益于几个启发式概念的结合,而不是单个特定的元启发式算法的实现。尽管有各种各样的实现,但它们都遵循一个通用算法
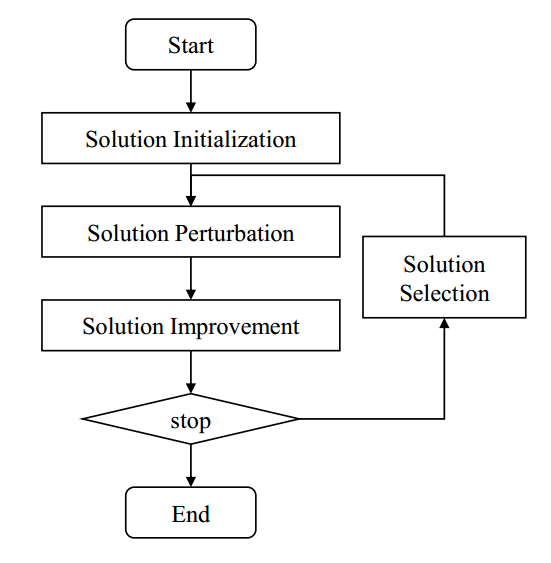
20年左右的SOTA
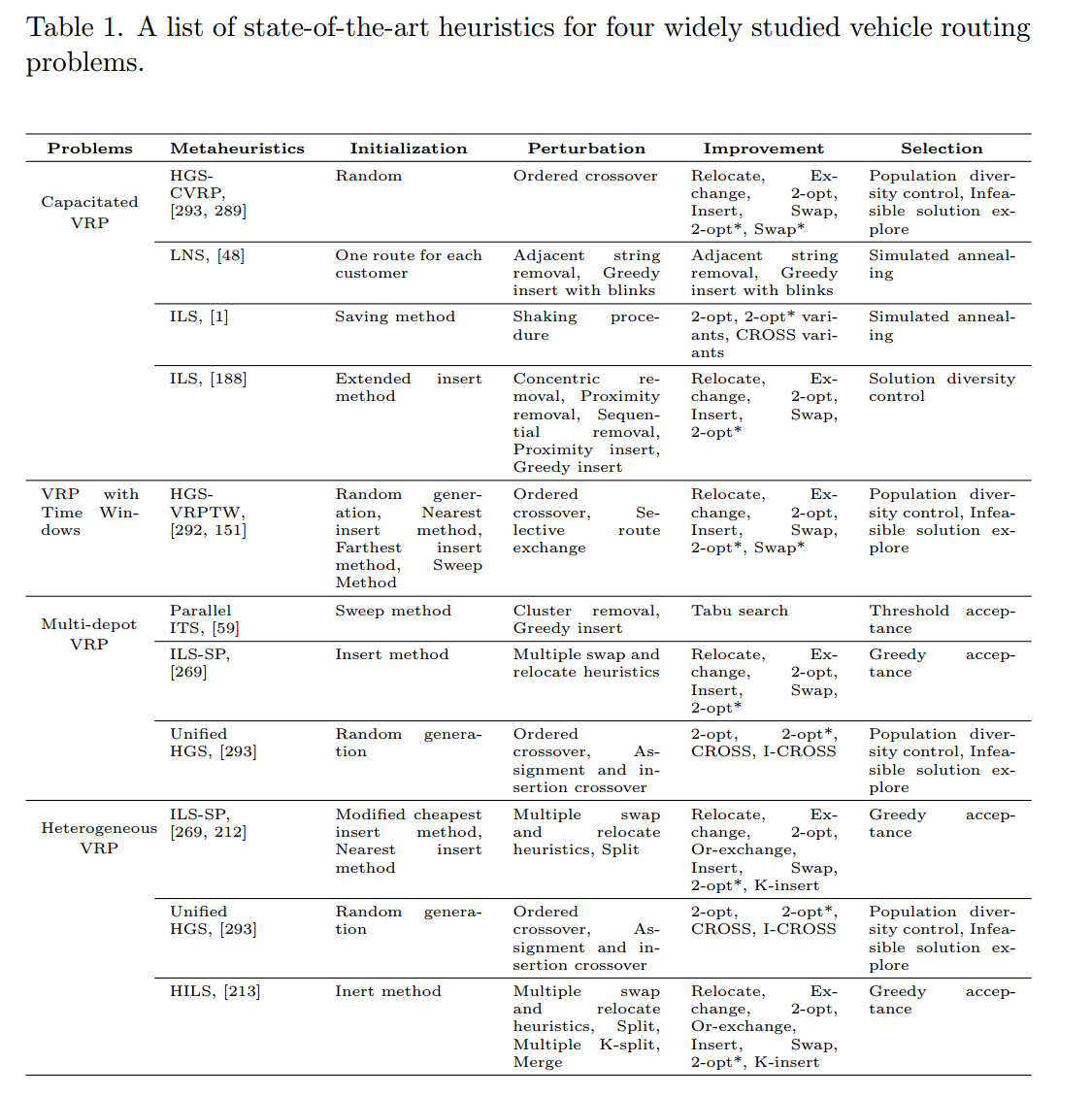
共性:
- 协作:多个方法的融合
- 初始化:减轻后续优化过程的负担,最终有利于全局收敛
- 解微调和改进
- 解方案的选择:避免贪心
- 两阶段范式
各种VRP及启发式
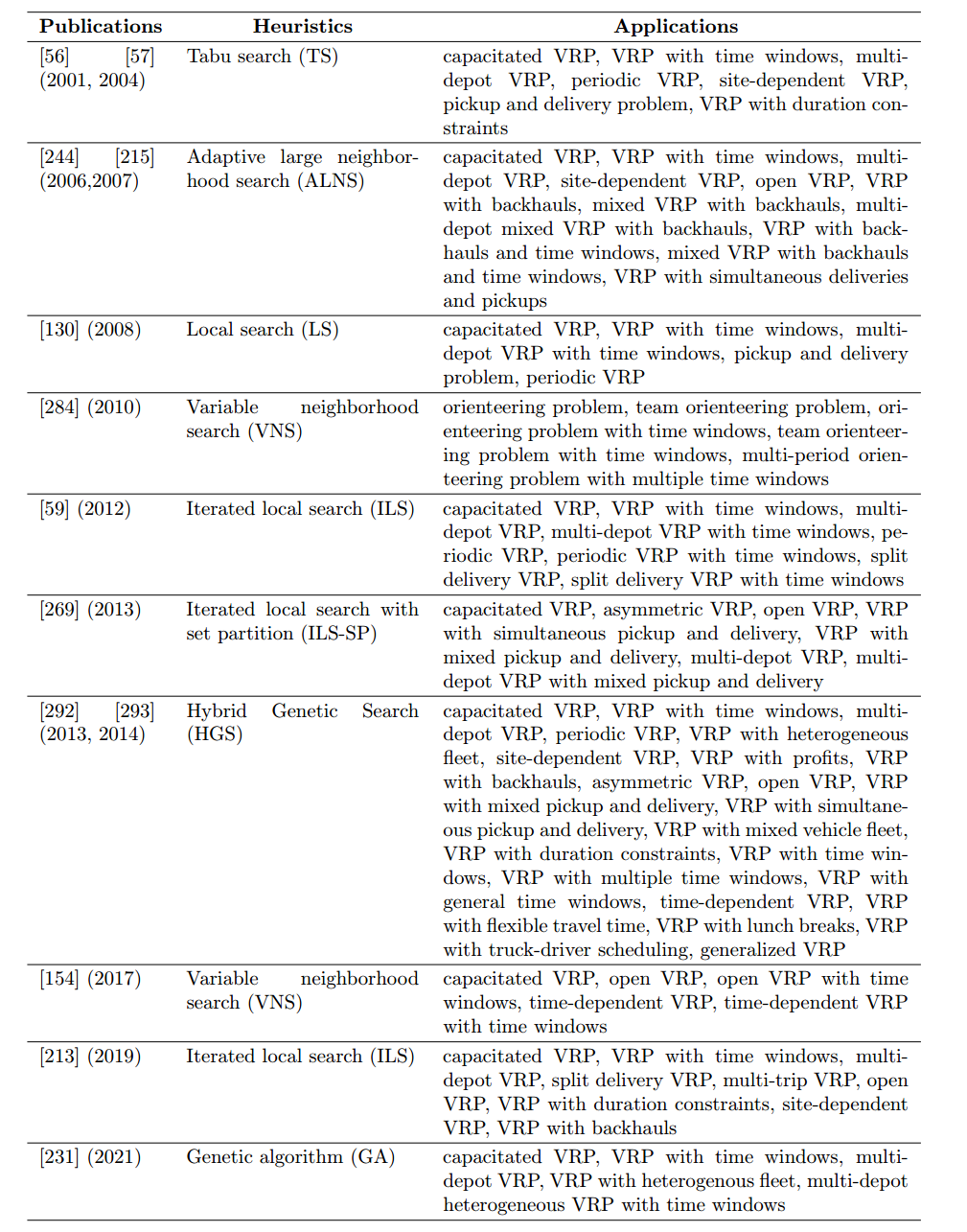
参考文献
[1] DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Management science, 1959, 6(1) : 80-91.
[2] Liu F, Lu C, Gui L, et al. Heuristics for vehicle routing problem: A survey and recent advances[J]. arXiv preprint arXiv:2303.04147, 2023.
[3] Du, L., He, R., 2012. Combining nearest neighbor search with tabu search for large-scale vehicle routing problem. Physics Procedia 25, 1536-1546.
[4] Vincent, F.Y., Redi, A.P., Hidayat, Y.A., Wibowo, O.J., 2017. A simulated annealing heuristic for the hybrid vehicle routing problem. Applied Soft Computing 53, 119-132.
[5] Wang, L., Lu, J., 2019. A memetic algorithm with competition for the capacitated green vehicle routing problem. IEEE/CAA Journal of Automatica Sinica 6, 516-526.
[6] Turkes, R., Sorensen, K., Hvattum, L.M., 2021. Meta-analysis of metaheuristics: Quantifying the effect of adaptiveness in adaptive large neighborhood search. European Journal of Operational Research 292, 423-442.
[7] Balseiro, S.R., Loiseau, I., Ramonet, J., 2011. An ant colony algorithm hybridized with insertion heuristics for the time dependent vehicle routing problem with time windows. Computers & Operations Research 38, 954-966.
[8] Pisinger, D., Ropke, S., 2007. A general heuristic for vehicle routing problems. Computers & operations research 34, 2403-2435.
[9] Reimann, M., Doerner, K., Hartl, R.F., 2004. D-ants: Savings based ants divide and conquer the vehicle routing problem. Computers & Operations Research 31, 563-591.
[10] Battarra, M., Golden, B., Vigo, D., 2008. Tuning a parametric clarke- wright heuristic via a genetic algorithm. Journal of the Operational Research Society 59, 1568-1572.
[11] Juan, A.A., Faul´ın, J., Jorba, J., Riera, D., Masip, D., Barrios, B., \2011. On the use of monte carlo simulation, cache and splitting techniques to improve the clarke and wright savings heuristics. Journal of the Operational Research Society 62, 1085-1097.
[12] Renaud, J., Boctor, F.F., 2002. A sweep-based algorithm for the fleet size and mix vehicle routing problem. European Journal of Operational Research 140, 618-628.
[13] Suthikarnnarunai, N., 2008. A sweep algorithm for the mix fleet vehicle routing problem, in: Proceedings of the International MultiConference of Engineers and Computer Scientists, Citeseer. pp. 19-21.
[14] Euchi, J., Sadok, A., 2021. Hybrid genetic-sweep algorithm to solve the vehicle routing problem with drones. Physical Communication 44,
101236.
[15] Lin, S., 1965. Computer solutions of the traveling salesman problem. Bell System Technical Journal 44, 2245-2269.
[16] Or, I., 1976. TRAVELING SALESMAN TYPE COMBINATORIAL PROBLEMS AND THEIR RELATION TO THE LOGISTICS OF REGIONAL BLOOD BANKING. Northwestern University.
[17] Gendreau, M., Hertz, A., Laporte, G., 1992. New insertion and post optimization procedures for the traveling salesman problem. Operations Research 40, 1086-1094.
[18] Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P., 1983. Optimization by simulated annealing. science 220, 671-680.
[19] Glover, F., 1986. Future paths for integer programming and links to artificial intelligence. Computers & operations research 13, 533-549.
[20] Baum, E., 1986. Iterated descent: A better algorithm for local search in combinatorial optimization problems. Manuscript .
[21] Shaw, P., 1997. A new local search algorithm providing high quality solutions to vehicle routing problems. APES Group, Dept of Computer Science, University of Strathclyde, Glasgow, Scotland, UK 46.
[22] Vincent, F.Y., Jewpanya, P., Redi, A.P., Tsao, Y.C., 2021. Adaptive neighborhood simulated annealing for the heterogeneous fleet vehicle routing problem with multiple cross-docks. Computers & Operations Research 129, 105205.
[23] ILHAN, I., 2021. An improved simulated annealing algorithm with crossover operator for capacitated vehicle routing problem. Swarm and Evolutionary Computation , 100911.
[24] Schermer, D., Moeini, M., Wendt, O., 2019. A hybrid vns/tabu search algorithm for solving the vehicle routing problem with drones and en route operations. Computers & Operations Research 109, 134-158.
[25] Sadati, M.E.H., C¸ atay, B., Aksen, D., 2021. An efficient variable neighborhood search with tabu shaking for a class of multi-depot vehicle routing problems. Computers & Operations Research 133, 105269.
[26] Maximo, V.R., Cordeau, J.F., Nascimento, M.C., 2022. Ails-ii: An adaptive iterated local search heuristic for the large-scale capacitated vehicle routing problem. arXiv preprint arXiv:2205.12082.
[27] Christiaens, J., Vanden Berghe, G., 2020. Slack induction by string removals for vehicle routing problems. Transportation Science 54, 417- 433.
[28] Kuo, R.J., Zulvia, F.E., Suryadi, K., 2012. Hybrid particle swarm optimization with genetic algorithm for solving capacitated vehicle routing problem with fuzzy demand{a case study on garbage collection system. Applied Mathematics and Computation 219, 2574-2588.
[29] Ariyani, A.K., Mahmudy, W.F., Anggodo, Y.P., 2018. Hybrid genetic algorithms and simulated annealing for multi-trip vehicle routing problem with time windows. International Journal of Electrical & Computer Engineering (2088-8708) 8.
[30] Euchi, J., Sadok, A., 2021. Hybrid genetic-sweep algorithm to solve the vehicle routing problem with drones. Physical Communication 44, 101236.
[31] Kalayci, C.B., Kaya, C., 2016. An ant colony system empowered variable neighborhood search algorithm for the vehicle routing problem with simultaneous pickup and delivery. Expert Systems with Applications 66, 163-175.
[32] Zhang, H., Zhang, Q., Ma, L., Zhang, Z., Liu, Y., 2019. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Information Sciences 490, 166- 190.
[33] Kool, W., Juninck, J.O., Roos, E., Cornelissen, K., Agterberg, P., van Hoorn, J., Visser, T., 2022. Hybrid genetic search for the vehicle routing problem with time windows: a high-performance implementation.
[34] KOK A L, MEYER C M, KOPFER H, et al. A dynamic programming heuristic for the vehicle routing problem with time windows and European Community social legislation[J]. Transportation Science, 2010, 44(4) : 442–454.
[35] Oriol Vinyals, Meire Fortunato, and Navdeep Jaitly. Pointer networks. In Advances in Neural Information Processing Systems, volume 28, pages 2692-2700, 2015.
[36] Hanjun Dai, Elias B Khalil, Yuyu Zhang, Bistra Dilkina, and Le Song. Learning combinatorial optimization algorithms over graphs. In Advances in Neural Information Processing Systems, pages 6351–6361, 2017.
[37] Iddo Drori, Anant Kharkar, William R Sickinger, Brandon Kates, Qiang Ma, Suwen Ge, Eden Dolev,Brenda Dietrich, David P Williamson, and Madeleine Udell. Learning to solve combinatorial optimization problems on real-world graphs in linear time. In International Conference on Machine Learning and Applications (ICMLA), pages 19–24, 2020.
[38] Wouter Kool, Herke van Hoof, and Max Welling. Attention, learn to solve routing problems! In International Conference on Learning Representations, 2018.
[39] Yeong-Dae Kwon, Jinho Choo, Byoungjip Kim, Iljoo Yoon, Youngjune Gwon, and Seungjai Min. POMO:Policy optimization with multiple optima for reinforcement learning. In Advances in Neural Information Processing Systems, volume 33, pages 21188–21198, 2020.
[40] Liang Xin, Wen Song, Zhiguang Cao, and Jie Zhang. Multi-decoder attention model with embedding glimpse for solving vehicle routing problems. In AAAI Conference on Artificial Intelligence, pages 12042–12049, 2021.
[41] Yan Jin, Yuandong Ding, Xuanhao Pan, Kun He, Li Zhao, Tao Qin, Lei Song, and Jiang Bian. Pointerformer:Deep reinforced multi-pointer transformer for the traveling salesman problem. In AAAI Conference on Artificial Intelligence, 2023.
[42] Minsu Kim, Jinkyoo Park, and Joungho kim. Learning collaborative policies to solve np-hard routing problems. In Advances in Neural Information Processing Systems, volume 34, pages 10418–10430, 2021.
[43] André Hottung, Yeong-Dae Kwon, and Kevin Tierney. Efficient active search for combinatorial optimization problems. In International Conference on Learning Representations, 2022.
[44] Hao Lu, Xingwen Zhang, and Shuang Yang. A learning-based iterative method for solving vehicle routing problems. In International Conference on Learning Representations, 2019.
[45] André Hottung and Kevin Tierney. Neural large neighborhood search for routing problems. Artificial Intelligence, page 103786, 2022.
[46] Yaoxin Wu, Wen Song, Zhiguang Cao, Jie Zhang, and Andrew Lim. Learning improvement heuristics for solving routing problems. IEEE Transactions on Neural Networks and Learning Systems, 33(9):5057–5069,2021.
[47] Yining Ma, Jingwen Li, Zhiguang Cao, Wen Song, Le Zhang, Zhenghua Chen, and Jing Tang. Learning to iteratively solve routing problems with dual-aspect collaborative transformer. In Advances in Neural Information Processing Systems, volume 34, pages 11096–11107, 2021.
[48] Yining Ma, Jingwen Li, Zhiguang Cao, Wen Song, Hongliang Guo, Yuejiao Gong, and Yeow Meng Chee.Efficient neural neighborhood search for pickup and delivery problems. In International Joint Conference on Artificial Intelligence, pages 4776–4784, 2022.
[49] Chaitanya K Joshi, Thomas Laurent, and Xavier Bresson. An efficient graph convolutional network technique for the travelling salesman problem. Arxiv preprint arxiv:1906.01227, ArXiV, 2019.
[50] Zhang-Hua Fu, Kai-Bin Qiu, and Hongyuan Zha. Generalize a small pre-trained model to arbitrarily large TSP instances. In AAAI Conference on Artificial Intelligence, 2021.
[51] Zhiqing Sun and Yiming Yang. Difusco: Graph-based diffusion solvers for combinatorial optimization.arxiv preprint arxiv:2302.08224, ArXiV, 2023.
[52] Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning, pages 2256–2265, 2015.
[53] Wouter Kool, Herke van Hoof, Joaquim Gromicho, and Max Welling. Deep policy dynamic programming for vehicle routing problems. In International Conference on Integration of Constraint Programming, Artificial Intelligence, and Operations Research, pages 190–213, 2022.
[54] RULAND K, RODIN E. The pickup and delivery problem: Faces and branch-and-cut algorithm[J]. Computers & mathematics with applications, 1997, 33(12) : 1 -13.
[55] ROPKE S, CORDEAU J-F. Branch and cut and price for the pickup and delivery problem with time windows[J]. Transportation Science, 2009, 43(3) : 267-286.
[56] Dumas, Y., Desrosiers, J., Soumis, F., 1991. The pickup and delivery problem with time windows. European Journal of Operational Research 54, 7-22.
[57] Ropke, S., Cordeau, J.F., Laporte, G., 2007. Models and branch-and-cut algorithms for pickup and delivery problems with time windows. Networks: An International Journal 49, 258–272.
[58] Ropke, S., Cordeau, J.F., 2009. Branch and cut and price for the pickup and delivery problem with time windows. Transportation Science 43, 267–286.