Prompt Learning for Generalized Vehicle Routing

Prompt Learning for Generalized Vehicle Routing

香港城市大学 张青富老师课题组、南方科技大学 王振坤老师课题组

华为诺亚方舟实验室

代码： https://github.com/FeiLiu36/PromptVRP

摘要

神经组合优化（NCO）是一种很有前途的基于学习的解决各种车辆路径问题的方法，无需大量的人工算法设计。然而，目前的NCO方法主要关注分布内性能，而实际问题实例通常来自不同的分布。可能需要昂贵的微调方法或从零开始的广义模型再训练来处理分布外实例。与现有方法不同，本文研究了一种有效的NCO交叉分布适应快速学习方法。具体而言，提出了一种新的快速学习方法，以促进预训练模型的快速零射击适应，以解决来自不同分布的路由问题实例。提出的模型在各种分布中学习一组提示，然后选择最匹配的提示，为每个问题实例提示预训练的注意力模型。大量的实验表明，提出的快速学习方法有助于快速适应预先训练好的路由模型。它在分布内预测和对各种新任务的零概率泛化方面也优于现有的广义模型。

介绍

NCO相比于启发式不需要太多的人工设计。

现有的神经组合优化方法大多集中于求解分布内实例，而现实中的路由问题实例通常来自不同的分布。因此，在不同分布情况下，它们的性能可能会急剧下降。最近的工作主要集中在提高分布外任务的泛化能力，这些方法中的大多数涉及使用元学习技术训练单个广义模型，它可以有效地适应不同分布的实例。然而，这些方法往往需要复杂且耗时的基于元学习的训练，并且学习能力受到固定模型结构的限制。

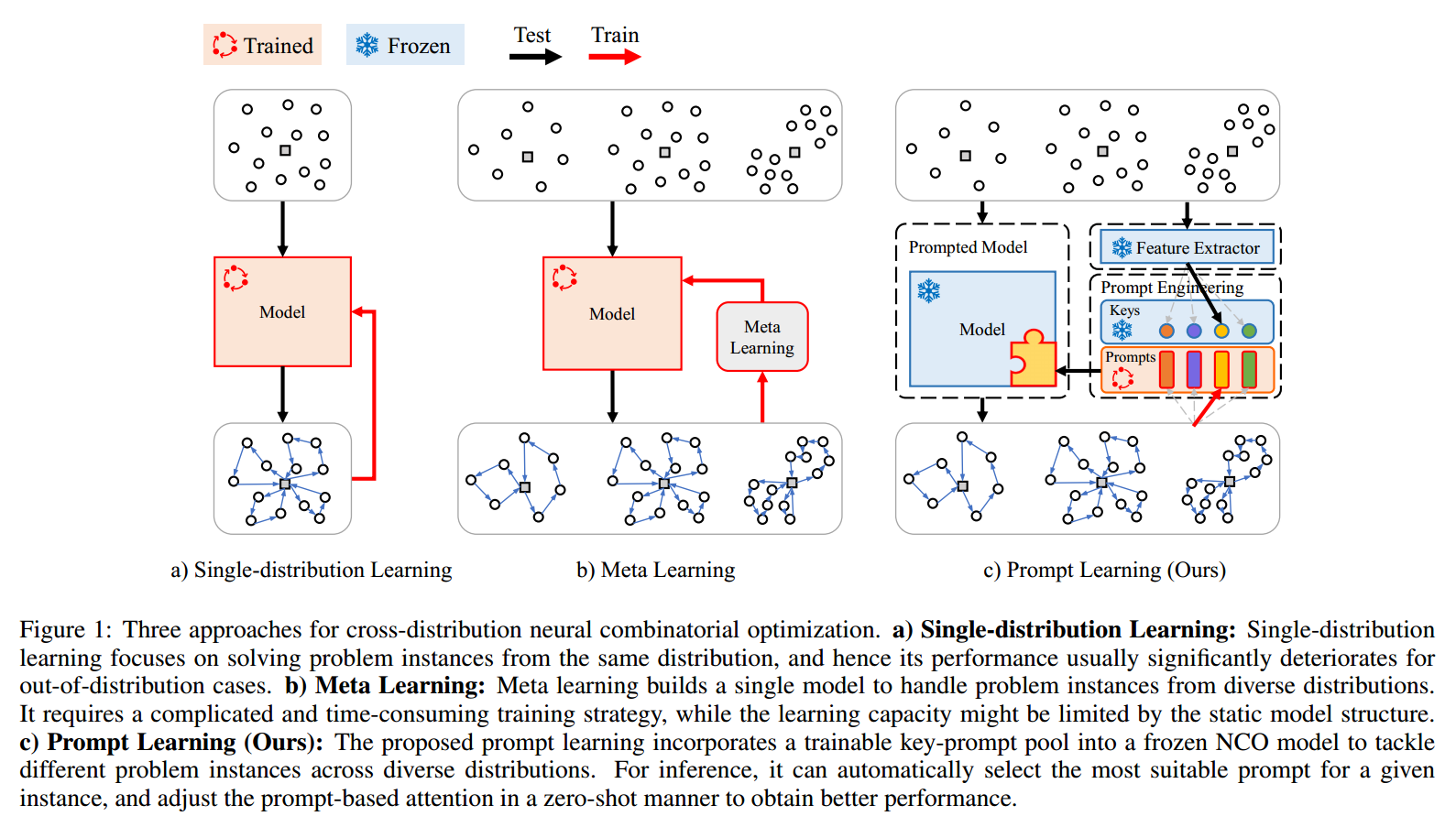
本文提出了一种新的方法，即使用提示学习使预训练的NCO模型能够快速自适应，以解决分发外路由问题实例。如图1所示，将预先训练好的编码器-解码器NCO模型保持固定，并有效地学习一组键提示对，这些键提示对被合并到模型中，用于处理来自不同分布的不同问题实例。交叉分布信息是通过共享提示来学习的。对于解决一个新的问题实例，将自动选择最合适的关键字，并使用其匹配的提示符以zero-shot的方式调整预训练的NCO模型，以获得更好的推理。这样，所提出的提示学习方法可以有效地扩展预训练的NCO模型的学习能力，表现出具有竞争力的泛化性能。

贡献：

• 研究了如何将提示学习纳入神经组合优化，并提出了求解交叉分布车辆路径问题的第一个提示学习方法。
• 开发了一种新颖有效的基于提示的注意力模型通过快速zero-shot自适应来处理来自不同分布的不同路由问题实例。
• 在广泛的交叉分布路由实例和基准实例上评估了提出的快速学习方法。与现有的元学习方法相比，的方法以更低的训练成本获得了更好的性能。

相关工作

• NCO：端到端构造和改进
• 交叉分布路由问题的NCO：为了提高路由问题的分布外泛化性能，已经开发了几种元学习方法。包括：多种几何分布下的鲁棒优化、对大规模问题的泛化、从问题规模和几何分布两方面考虑了泛化。现有的工作大多采用单一的广义模型，并使用元学习方法来提高交叉分布性能，这可能会导致训练时间长，学习能力受限。
• 提示词学习：主要在CV和NLP。近年许多训练有素的模型被开发用于组合优化。然而，这些预训练模型的有效利用还没有得到充分的研究。本文提出了一种快速学习方法，以有效地适应固定的预训练模型来解决交叉配送车辆路线问题。

对路由进行提示学习

问题表述

问题建模：CVRP

将无向图 $G=(V, E)$ 上的基本有容量的车辆路径规划问题（CVRP）表示为 $V=\lbrace v_0, \ldots, v_n\rbrace $，其中 $v_0$ 是仓库，$v_1, \ldots, v_n$ 是 $n$ 个客户。$V_c=\lbrace v_1, \ldots, v_n\rbrace $ 是客户集合。对于第 $i$ 个客户，有一个需求 $d_i$。$E=\lbrace e_{ij}\rbrace $，其中 $i, j \in \lbrace 1, \ldots, n\rbrace $ 是每两个节点之间的边。对于每条边 $e_{ij}$，都有一个相关的成本（距离）$c_{ij}$。一组同类车辆以容量 $C$ 从仓库出发，访问客户并返回仓库。所有客户的需求都必须得到满足。每个客户必须被访问一次。目标是最小化所有路径的总旅行距离，同时满足所有约束条件。

主要思想与基本框架

典型的基于构造的 NCO 方法 ：AM

其中 $\mathcal{G}$ 代表给定实例，$\theta$ 是模型参数，$\tau$ 是模型构造的轨迹（例如行程）。目标是找到最佳模型参数 $\theta^\ast$ 以最小化给定分布 $p(\mathcal{G})$ 下 $\tau$ 的平均总距离（作为训练损失 $\mathcal{L}$）。

在模型训练中明确考虑多种分布时，大多数现有工作将每个分布视为一个任务，并使用元学习进行模型训练。目标是学习一个单一且强健的模型参数 $\theta^\ast$，能够在各种分布上很好地推广：

其中 $T$ 是任务的数量，$p(\mathcal{G})$ 表示第 $i$ 个任务的分布。

与这两种方法不同，建议将提示学习融入 NCO 模型，以解决跨分布的车辆路径规划问题。目标可以表述为：

其中 $\lbrace P_1, \ldots, P_M\rbrace $ 是 $M$ 个提示，而 $P$ 是每个给定实例的选定提示。在这个基于提示的模型中，可以学习这 $M$ 个提示，而不是整个模型参数集合 $\theta$。这里的目标是学习最佳提示，以适应具有固定 $\theta$ 的预训练模型，以实现跨分布的性能。

如图 1 所示，提出的提示学习包含三个主要组件：1) 特征提取器，2) 提示工程，3) 提示模型。采用预训练的注意力网络作为特征提取器和模型，在训练和测试过程中保持固定。键也是根据随机生成的训练实例的特征预先确定的。唯一可调节的组件是提示。输入实例同时输入到模型和特征提取器中。特征提取器将输入实例转换为特征向量，使能够从键-提示对池中识别最合适的键，以匹配输入特征。键和提示是耦合在一起的。然后使用最佳匹配键的相关提示来提示预训练模型。提示模型基于所选提示生成解决方案。该解决方案用于计算奖励，以便在训练过程中更新所选提示。

特征提取器

在本工作中，直接使用AM 作为特征提取器。编码器由 $L$ 个堆叠的多头注意力（MHA）块组成。编码器的输入是节点特征 $f_i, i=1, \ldots, n$。在的实验中，第 $i$ 个节点的输入特征表示为 $f_i=\lbrace x_i, y_i, d_i\rbrace $，其中 $\left(x_i, y_i\right)$ 是坐标，$d_i$ 是需求。输入特征通过线性投影嵌入，以生成初始特征嵌入 $h_i^{(0)}$。在每个 MHA 层中使用跳跃连接和实例归一化（IN）：

其中 $l$ 和 $l-1$ 分别表示当前和上一个嵌入层。前馈（FF）层包含一个具有 ReLU 激活的隐藏子层。上述编码过程生成最终的节点嵌入 $h_i^{(L)}$。

不同于 CV 和 NLP 中常用的特征提取方法，该方法使用特定隐藏层的嵌入，将来自多个层的嵌入进行连接。具体来说，在每个 MHA 的输出层（在归一化之前）进行连接：

其中 $F^l$ 是第 $l$ 个 MHA 的最后归一化层之前的隐藏嵌入，$F$ 是所有 $L$ 层的连接特征。每个隐藏嵌入 $F^l$ 在所有 $n$ 个节点上求平均，以促进跨不同问题的大小的泛化。提示工程的最终输出特征通过标准尺度化进行调整，表示为 $F = (F−mean)/stand$，其中 $mean$ 和 $stand$ 分别表示预处理实例的均值和标准差。这些预处理实例用于确定键。平均值和标准偏差是按元素计算的。

提示词工程

维护一个key-提示对池，该池由 $M$ 对key-提示对 $\left\lbrace K_i, P_i\right\rbrace , i=1, \ldots, M$ 组成，其中 $K_i$ 和 $P_i$ 分别是第 $i$ 个key和提示。每一对都有一个固定的key和一个可学习的提示。对于每个输入特征 $F_i$，找到最佳匹配的key $\hat{K}=\min S\left(F_i, K_j\right), j=1, \ldots, M$，其中 $S()$ 是距离函数。使用的距离函数是输入特征与key之间的欧几里得距离。与 $\hat{K}$ 相关联的提示 $\hat{P}$ 随后被选中以提示预训练的神经求解器。在每个包含 $B$ 个实例的批次中，选择 $B$ 个key，并在训练过程中更新相关的 $B$ 个提示。

key $K_i, i=1, \ldots, M$ 是预先确定的向量，其大小与特征相同。在整个训练过程中保持不变。从341个分布中随机抽取128个实例，总共生成43648个实例以生成特征数据。对于每个实例 $i$，利用在公式 (5) 中介绍的特征提取器提取特征 $F_i$。根据问题规模将样本分为四组。对于每组，使用K均值聚类将样本聚类为 $N$ 个簇。特征的簇中心随后被用作key。最终，获得 $M=4 \cdot N$ 个向量簇中心，作为提示学习的key。

对于每个key $K_i$，根据均匀分布随机初始化一个向量作为相关联的提示 $P_i$，并将提示缩放到 $[-1,1]$ 范围内。

key-提示对仅在使用上相关联，意味着相关的提示是基于所选key使用的。尽管它们的值是解耦的，在训练过程中仅在固定key的情况下更新提示。结构故意保持简单，而不动态调整key和提示。此外，key和提示的大小也不同。前者由特征大小决定，而后者应足够长以提示预训练模型。

提示模型

选择著名的 AM 作为预训练模型，因为它被广泛应用于各种路由问题。该模型由一个六层编码器和一个单层解码器组成。在推理过程中，编码器进行一次推理，由解码器迭代生成目标路由实例的解。选择的提示用于提示六层编码器，这允许对预训练的注意力模型进行更多的控制。

编码器 预训练编码器的结构与用于特征提取器的结构相同。它由六层多头自注意力（MHA）组成，实例特征 $f_i$ 的线性投影 $h_i^{(0)}$ 作为输入，最终节点嵌入 $h_i^{(L)}$ 作为输出。

提示编码器 从提示工程中选择的提示 $P$ 首先被拆分成 $L$ 个子提示 $P^l, l=1, \ldots, L$。每个子提示 $P^l$ 用于预训练编码器的相应嵌入层。$P^l$ 的长度为 $D \cdot E$，其中 $D$ 是标记的数量，$E$ 是标记的长度。然后，第 $l$ 个子提示 $P^l$ 被重塑为 $D$ 个提示标记 $p_i^{(l)}, i=1, \ldots, D$：

这些标记被拼接到编码器的相应第 $l$ 层中。具体而言，对于第 $l$ 个 MHA，$D$ 个提示标记与输入的隐藏层拼接如下：

因此，第 $l$ 层 MHA 的输入标记长度总是比第 $l-1$ 层的输入标记多 $D$。在编码器的最后一层将会有 $n+L \cdot D$ 个输出嵌入标记。我们仅使用前 $n$ 个输出嵌入标记作为解码器的输入，而不是所有的 $n+L \cdot D$ 个标记。前 $n$ 个嵌入标记代表实例的 $n$ 个节点，这些节点由 $L \cdot D$ 个提示标记控制。

解码器 解码器顺序构建解决方案。它由一个 MHA 层和一个带有剪枝的单头注意力（SHA）层组成。MHA 与编码器中使用的稍有不同，此处不使用跳跃连接、实例归一化和 FF 子层。推理的第 $t$ 步如下：

其中 $h_t^{(L)}$ 和 $a_t$ 分别表示第 $t$ 步中选定节点和属性的嵌入。MHA 的输出嵌入 $\hat{h}_c$ 被用作 SHA 的输入。SHA 使用掩蔽的不满足节点输出选择下一个节点的概率，采用 $\operatorname{softmax} p_i=\frac{e^{u_i}}{\sum_j e^{u_j}}$。

强化学习训练方法

REINFORCE

实验

实验设置

• 模型设置：16个提示、每层提示token数量 $D=5$
• 数据分布：341个
• 训练：epoch的最大数目是10,000，每个epoch有1,000个实例。11 GB GPU内存的RTX 2080Ti上，只需要大约2.5天
• baseline
  • 启发式：混合遗传搜索（HGS）、LKH3
  • NCO：单分布POMO、车辆路径问题全泛化元学习方法（Omni）

实验结果

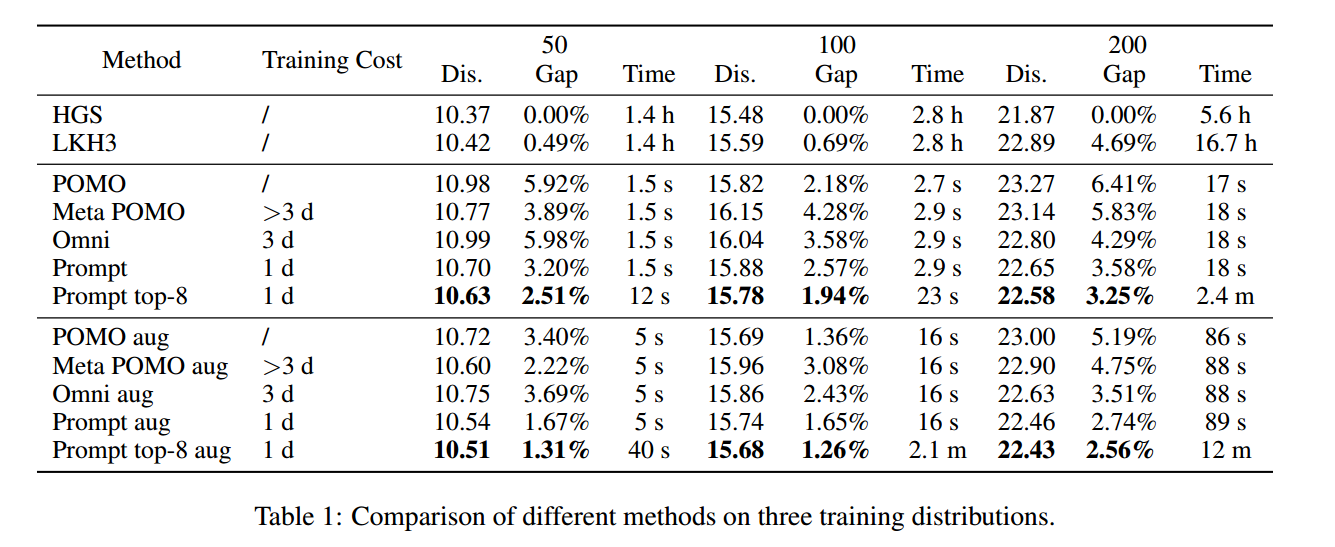
规模50 和 100，分别以5秒和10秒的时间限制执行HGS和LKH。当问题大小为200时，分别设置 20s 60s。aug是数据增强。

泛化实验

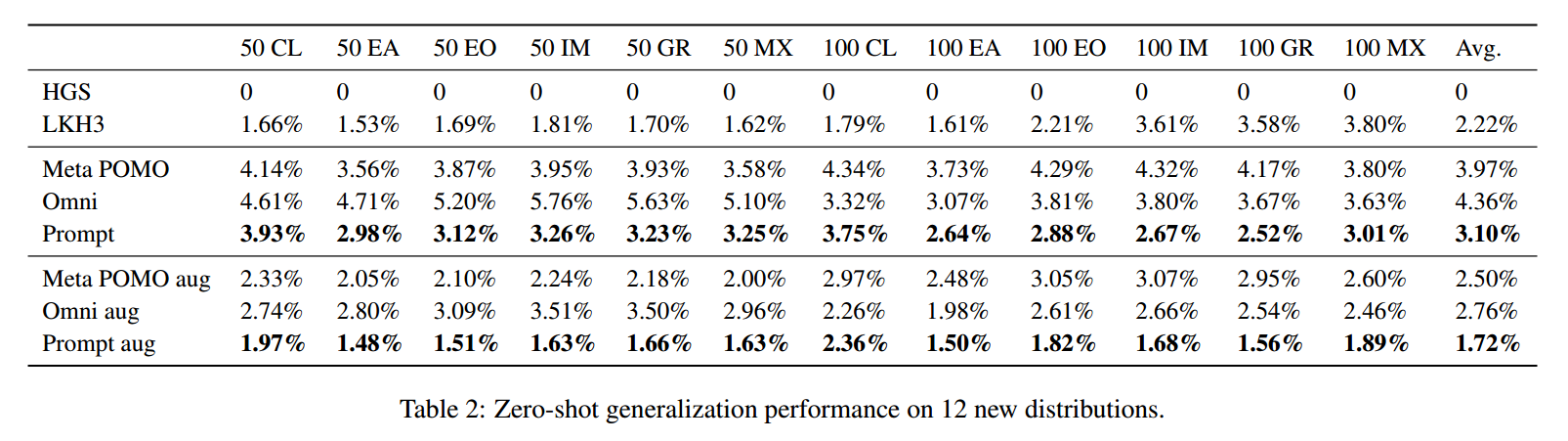
包括聚类（CL）、扩展（EA）、爆炸（EO）、内爆（IM）、网格（GR）和混合（MX）

Top-K 提示词

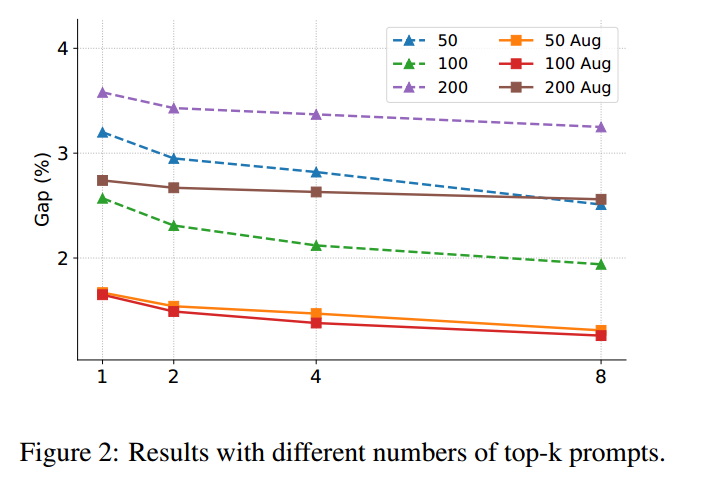
通常，性能随着提示数量的增加而提高。

差距的减少与使用的提示数并不是线性正比的，这表明最匹配的提示比其他提示更重要。

提示词 token 大小

对比了 token 1 5 10

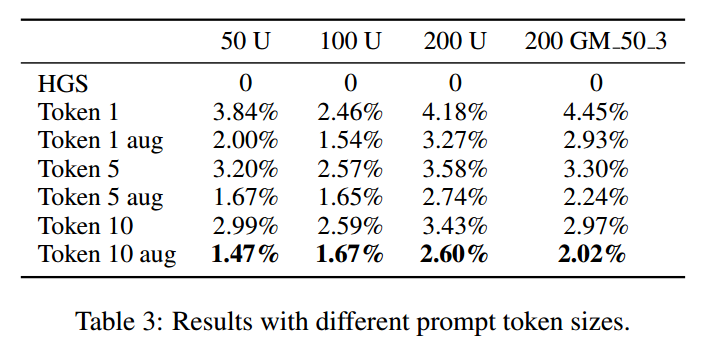
U和GM分别代表3个聚类的均匀分布和按50进行缩放的高斯分布。

真实世界实例

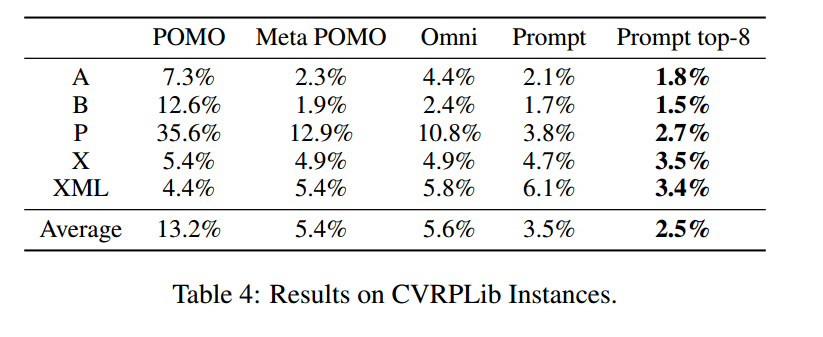
展示了和最佳实例的gap。

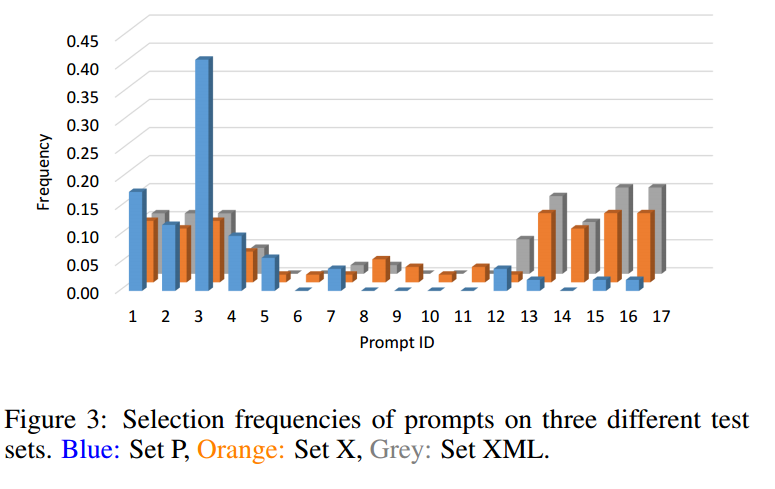
可视化了测试集P、X和XML上16个提示的选择频率（标准化）。集合X和集合XML的频率分布相似，但与集合P不同。例如，集合X和XML经常使用11-15提示符，而在集合p中很少使用。

总结

本文研究了第一个基于提示学习的神经组合优化（NCO）方法来解决不同分布下的车辆路径问题。提出了一种基于提示的注意力网络，其中包含一个可学习的key-prompt对池，以促进预训练的NCO模型的快速zero-shot适应交叉分布泛化。为了评估提出的快速学习方法的有效性，在不同分布的测试实例上进行了大量的实验。结果清楚地表明，优于经典的单分布学习方法和现有的元学习技术。基于提示的模型在分布内预测和zero-shot泛化方面都有改进，同时训练成本更低。

• Previous
  ReinforceNS Reinforcement Learning-based Multi-start Neighborhood Search for Solving the Traveling Thief Problem
• Next
  Learning to Solve Class-Constrained Bin Packing Problems via Encoder-Decoder Model