Learning to Solve Class-Constrained Bin Packing Problems via Encoder-Decoder Model

学习用编码器-解码器模型解决类约束的装箱问题

海康威视研究院

ICLR 2024

摘要

神经方法在解决组合优化（CO）问题（包括装箱问题（Bin Packing Problem, BPP））方面显示出显著的优点。然而，大多数现有的基于ml的方法侧重于几何BPP，如3DBPP，而忽略了复杂向量BPP。在本研究中，我们引入了一个向量BPP的变体，称为类约束装箱问题（Class-Constrained Bin Packing Problem, CCBPP），处理类别和大小的物品，目标是将物品装箱在最小数量的箱子中，考虑到箱子的容量和它可以容纳的不同类别的数量。为了提高求解CCBPP的效率和实用性，我们提出了一种基于学习的编码器-解码器模型。编码器采用图形卷积网络（GCN）生成热图，表示不同物品打包在一起的概率。解码器通过集群解码和主动搜索方法对解决方案进行解码和微调，从而为CCBPP实例生成高质量的解决方案。大量的实验表明，我们提出的方法始终如一地为各种CCBPP提供高质量的解决方案，与最优方案的差距很小。此外，我们的编码器-解码器模型在CCBPP的一个实际应用——制造订单整合问题（Manufacturing Order Consolidation Problem, OCP）上也显示出有希望的性能。

介绍

基于学习的方法在求解效率和泛化能力方面都优于精确求解法和近似启发式。

装箱主要有两种概括，几何装箱和向量装箱。大多数基于学习的BPP求解器关注的是几何BPP，如离线和在线3D装箱问题（3DBPP），它通常指的是将一组长方体形状的物品分别沿着x、y和z轴以轴线对齐的方式打包到最小数量的箱子中。这些方法通常利用注意力网络或卷积神经网络作为编码器，以更好地表示空间约束，并通过强化学习（RL）学习顺序构建解决方案，RL从生成的打包序列中学习求解器。另一方面，具有多种性质和复杂约束的向量BPP在神经CO问题领域受到的关注有限。向量BPP的一个典型例子是类约束装箱问题（Class-Constrained Bin Packing Problem, CCBPP），它处理的是类和大小的物品，目标是在考虑到箱子容量和它可以容纳的不同类的数量的情况下，将物品打包在最少的箱子里。

本文的工作旨在学习一种新的基于学习的模型，该模型可以有效地解决具有多种属性和复杂约束的各种CCBPP。在CCBPP中，只需要注意装箱顺序，而不需要考虑3DBPP中需要考虑的位置和方向。然而，一个最优的装箱结果总是对应于多个装箱序列，因为每个箱子内的物品的顺序不影响装箱解决方案，但会直接改变装箱序列。因此，当仅仅依赖于从打包序列中学习时，它带来了复杂性。为了克服这些挑战，引入连接矩阵作为标签来表示不同的物品是否在最优结果中打包在一起。如果将两项打包在一起，则矩阵中对应的值为1，否则为0。与生成的打包序列相比，连接矩阵提供了更丰富的信息。

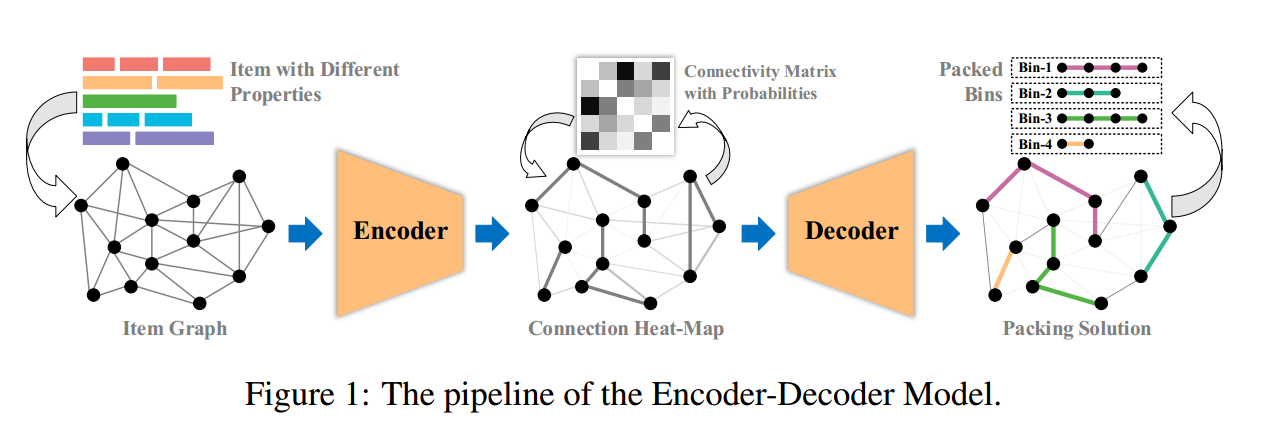
在本文中，提出了一个基于学习的编码器-解码器模型来获得CCBPP的近似解，如图1所示。涉及到基于物品信息的图的构建，因为物品的大小和类别可以通过图结构有效地表示。训练标签被定义为描述各个物品之间关系的真实连接矩阵。利用GCN来训练编码器，以便生成具有概率的连接矩阵，也被视为测试实例的热图。在编码器经过良好的训练后，聚类解码器尝试将热图矩阵解码为物品序列。然而，测试实例可能与训练样本的分布存在显著差异，这可能导致相对较差的性能。因此，在解码过程中使用主动搜索技术来微调最终解决方案，利用特定于实例的特征来确保解决方案的质量。本文模型不同于传统的编码器-解码器结构来解决CO问题， Encoder和Decoder是两个分离的部分，具有不同的用途，这使得Encoder更容易从连接矩阵中学习，并且在实际场景中应用将更加灵活。

总的来说，主要贡献总结如下：

给出了CCBPP的明确定义，并详细介绍了CCBPP的一个实际应用——制造订单整合问题（OCP）。证明CCBPP和OCP可以表示为向量BPP的特殊变体。
引入了一个新的模型来解决装箱问题，首先通过GCN对属性和主导约束进行编码，生成不同物品的连接概率，并根据一个实例的特定属性解码最佳解决方案。据我们所知，本文第一个提出了一种基于学习的方法来求解复杂向量BPP。
在CCBPP合成数据集和现实世界的OCP数据集的各种设置上进行了大量的实验，结果表明算法可以获得比其他基准更好的解决方案，同时花费的时间也更少。

问题描述

CCBPP

给定整数 $B,C,Q$，一个物品集合 $\lbrace 1,\cdots,N\rbrace$，第 $i$ 个物品的大小是 $s_i$，类别是 $c_i\in\lbrace 1,\cdots, Q\rbrace$。

需要对物品装箱，每个箱子的最大大小是 $B$，最多只能有 $C$ 个不同的类别。

CCBPP 的目标是最小化箱子的数量。

订单整合问题 OCP

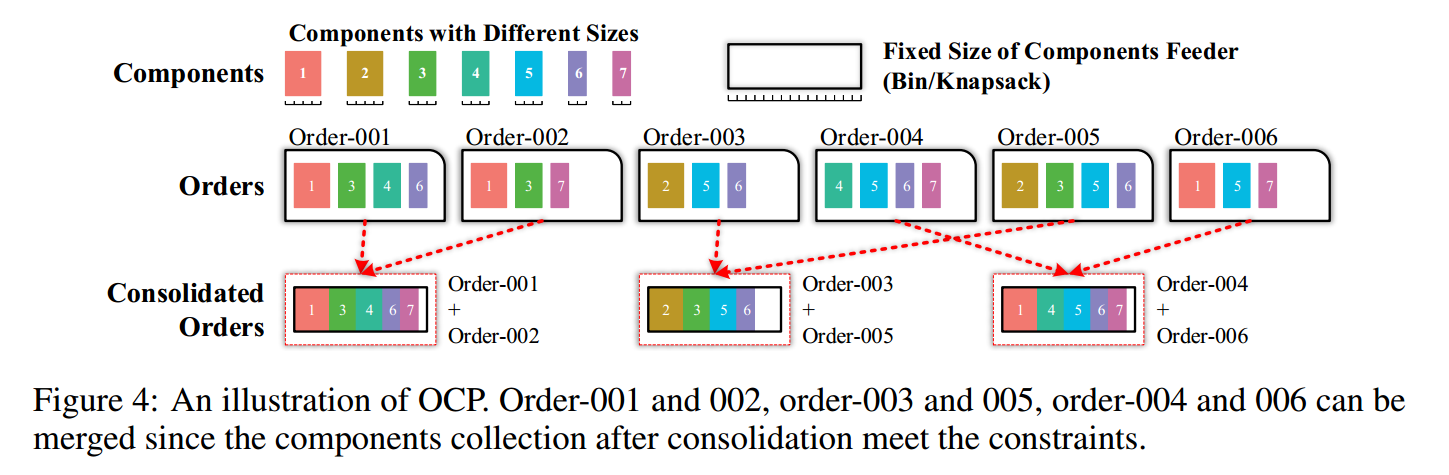
有多个订单，每个订单包含不同种类的部件。

一个机器能够处理多个订单，只要订单中部件的种类和不超过机器处理的最大种类即可。

目标是最小化合并后的订单总数。

对应一个物品有多个种类的CCBPP。

方法

框架

输入：物品的属性

根据问题的变量和约束构造一个图
用图卷积网络对输入图进行编码，生成热图，热图表示两个物品在一个箱中的概率
利用聚类解码将热图解码成序列
根据具有主动搜索的特定样本的特征输出最终解决方案

编码器

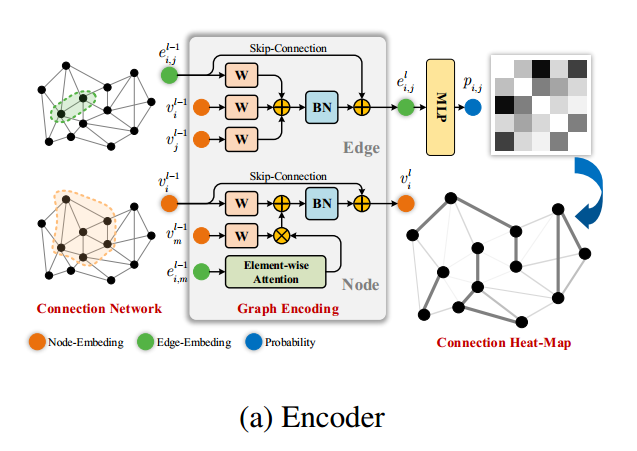
节点属性 $x_v$ 表示物品的属性，如大小和种类。

边属性 $x_e$ 表示两个物品的关系，使用类余弦相似性作为边特征。如果两个物品没有共享类，零余弦相似度被替换为一个小常数。

GCN输出提供了两个项目被打包在一起的概率。

计算方式如下

\[\begin{aligned} v_i^0 & =A_v x_v+b_v \\ e_{i j}^0 & =A_e x_e+b_e \end{aligned}\] \[\begin{gathered} a t t n_{i, j}^l=\exp \left(W_0^l e_{i, j}^{l-1}\right) \oslash \sum_{(i, m) \in E^*} \exp \left(W_0^l e_{i, m}^{l-1}\right) \\ v_i^l=v_i^{l-1}+\operatorname{Re} L U\left(B N\left(W_1^l v_i^{l-1}+\sum_{(i, m) \in E^*} a t t n_{i, j}^l \odot W_2^l v_j^{l-1}\right)\right) \\ e_{i, j}^l=e_{i, j}^{l-1}+\operatorname{Re} L U\left(B N\left(W_3^l v_i^{l-1}+W_4^l v_j^{l-1}+W_5^l e_{i, j}^{l-1}\right)\right) \end{gathered}\] \[p_{i, j}=\frac{\exp \left(\operatorname{Re} L U\left(W_6 e_{i, j}^L\right)\right)}{\exp \left(\operatorname{Re} L U\left(W_6 e_{i, j}^L\right)\right)+1}\]

网络通过监督学习训练。为了更好地得到热图的聚类特征，损失应该同时包含预测误差和聚类偏差。具体来说，损失函数包括加权交叉熵损失 $L_{ce}$ 和模损失 $L_m$ 两部分。

\[\begin{gathered} L_{c e}=-\frac{1}{\gamma|V|} \sum_{i, j} \hat{p}_{i, j} \log p_{i, j} w_1+\left(1-\hat{p}_{i, j}\right) \log \left(1-p_{i, j}\right) w_0 \\ L_m=-\frac{1}{\gamma|V|} \sum_{i, j} p_{i, j} \cdot \hat{p}_{i, j}-p_{i, j} \end{gathered}\]

$L_{ce}$ 计算预测概率与真实值之间的距离。为了避免正负样本不平衡，对其进行加权，$w_0=\frac{N^2}{N^2-2N},w_1=\frac{N^2}{2N}$。

最小化 $L_m$ 意味着最大化由标签表示的应该打包在一起的概率。

最终损失 $L_{tot}=L_{ce}+\lambda L_m$。

解码器

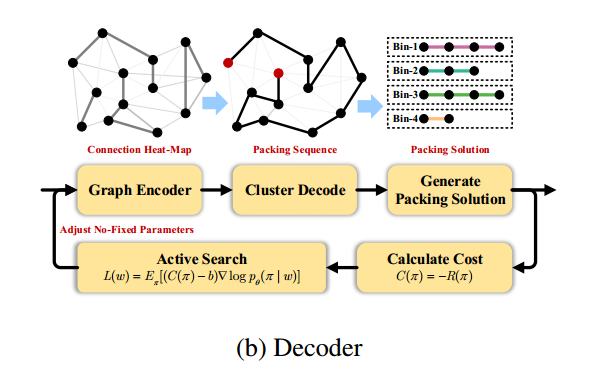
在这个解码阶段之后，装箱结果随后通过FF从装箱序列中导出。将选择最佳结果，并通过所选解决方案的反向传播更新网络，从而更改生成的热图。经过几轮网络更新后，装箱解决方案的质量会有明显的提高。

TSP中常用的 greedy 解码和 sample 解码通常只关注最后一项而忽略了其他项，而装箱问题则需要综合考虑所有被装箱的项并汇总相关信息。可以利用聚类算法（如K- nearest Neighbors）将物品分成几个部分，但被划分的物品部分可能无法打包在一个箱子中，因此最终的解决方案可能与K有很大的不同。因此提出了聚类解码器：

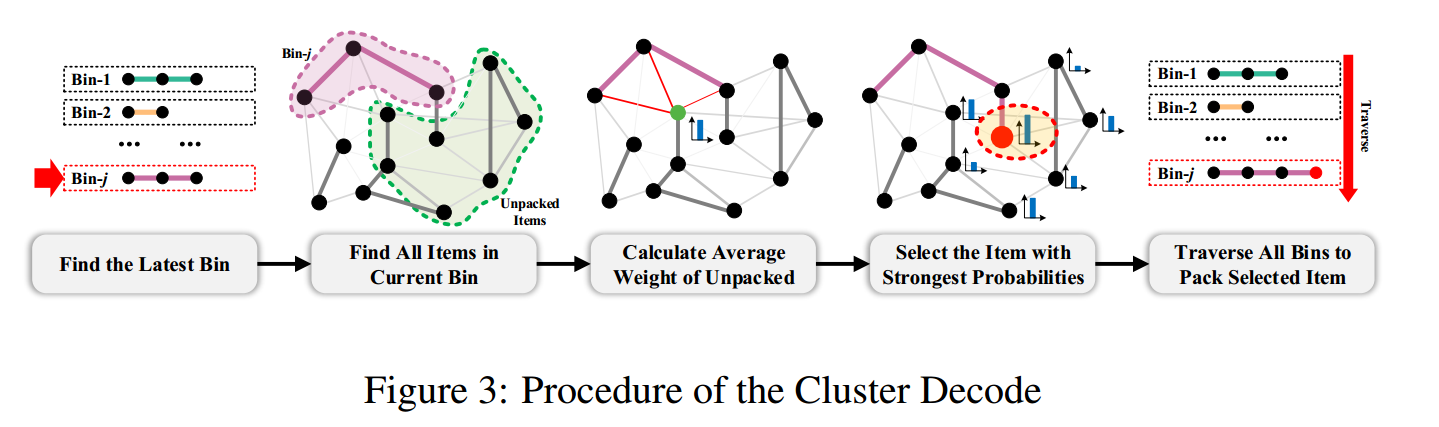
开始时，随机选取一个项目，并将索引设置为序列的第一个，通过 FF(First Fit) 算法将该项目放入第 $j$ 个箱子。然后遍历所有的箱子并找到最近打开的一个 $B_m$。由于新选择的物品最有可能被装入最新的箱子中，因此下一个物品由热图 $P$ 表示的 $B_m$ 中所有物品的平均连接概率选出。该序列一直生成，直到访问了所有 $N$ 个项目。

主动搜索

由于训练样本和测试样本的分布可能不相同，因此得到的解与最优解之间存在显著差异。

可以利用强化学习来根据目前看到的解决方案微调打包序列。

利用基于强化学习的主动搜索来微调预训练的网络。由于只有少数样本被用于微调，冻结了大部分图网络，只更新了一个基于策略梯度的强化学习损失函数嵌入层。解码代价 $C(\pi)=-R(\pi)$，调整强化学习参数 $w$ 最小化 $L(w)$

\[L(w=)E_{\pi}[(C(\pi)-b)\bigtriangledown\log p_\theta (\pi | w)]\]

其实就是REINFORCE。

评估表现

物品大小：10 - 25

箱子容量：100

种类数量：单类版本（10、20、30）、多类版本（20、30）

类约束值：$C=5$

每个物品属于类数：2、3

训练实例：6400

测试实例：200

最优目标函数：都是20

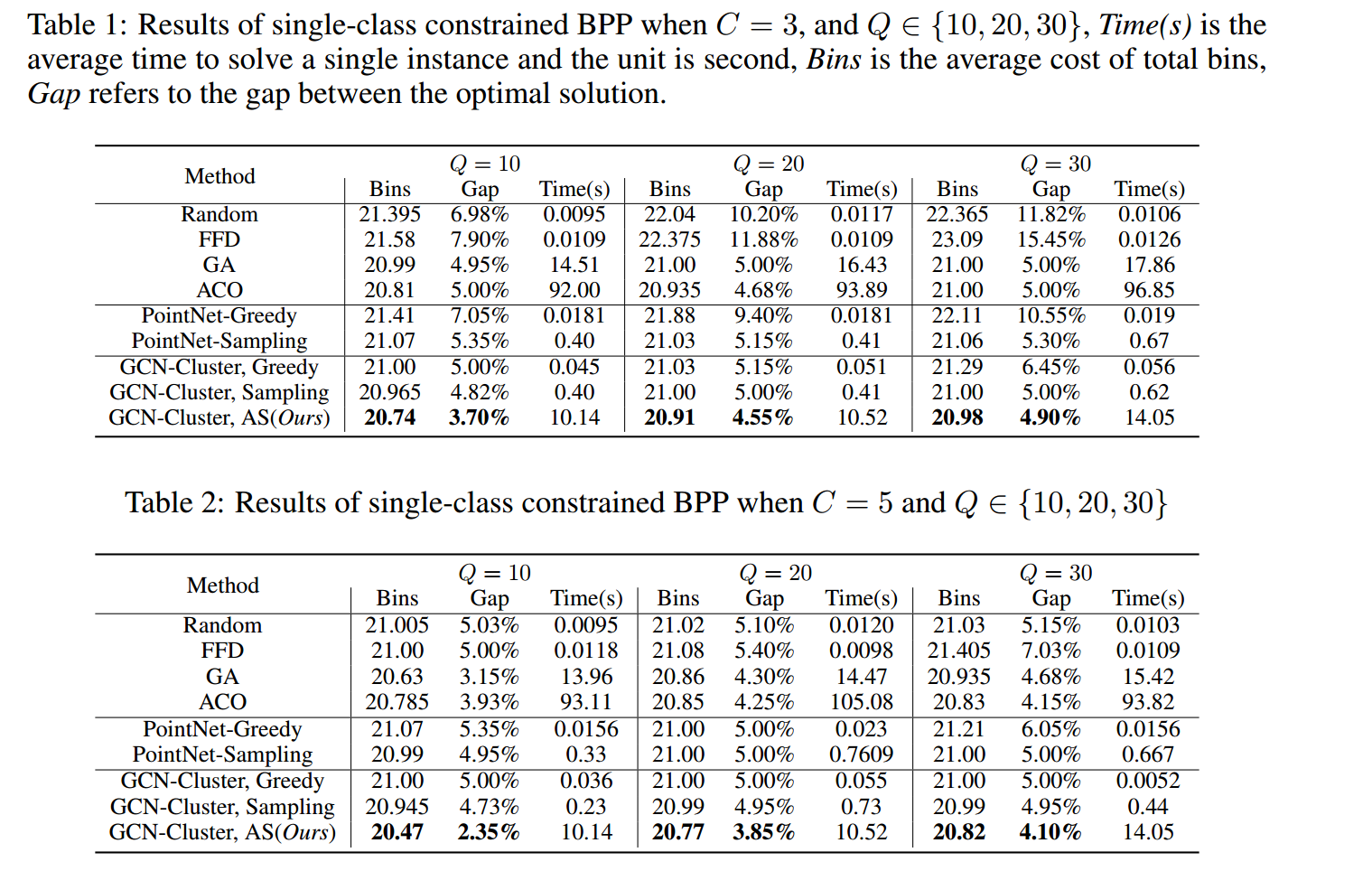
单类结果：

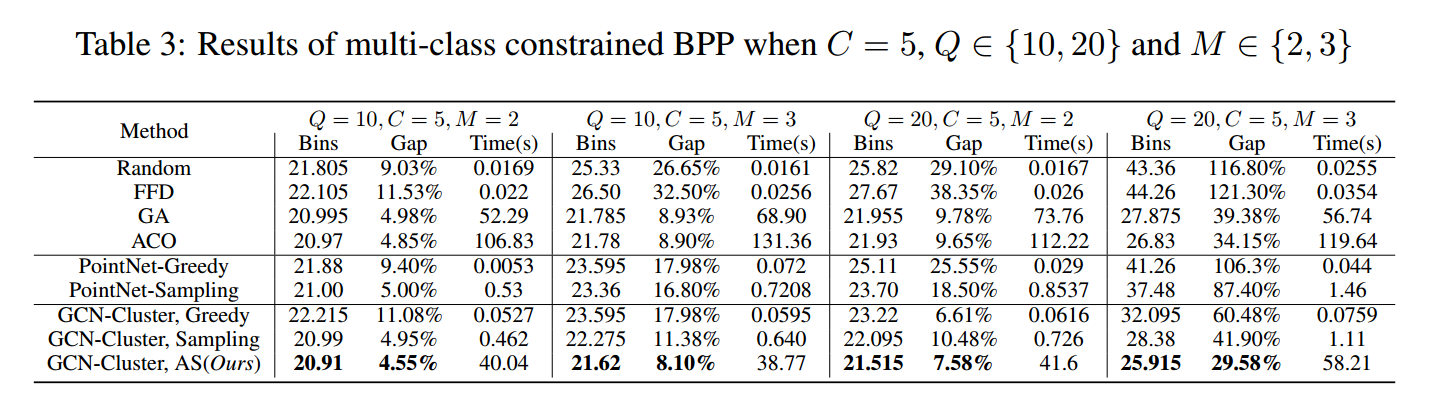
多类结果：

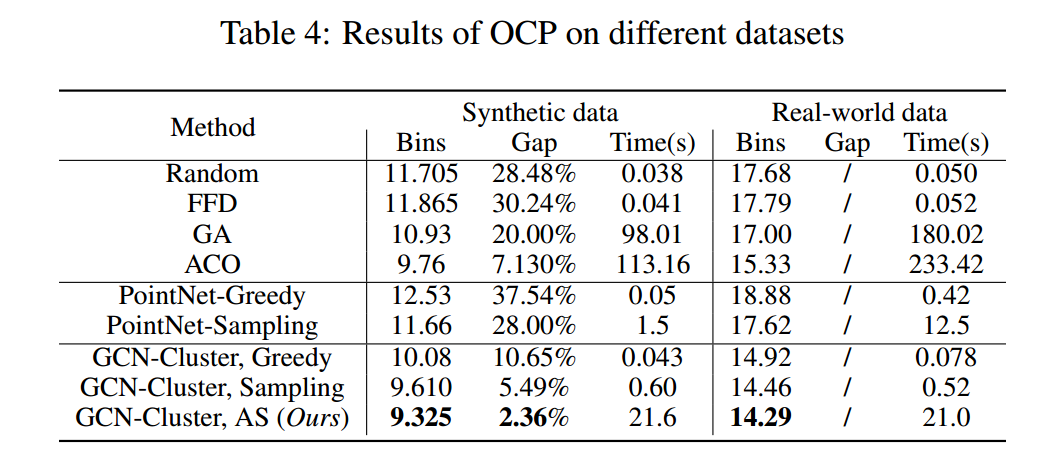
案例研究：订单整合问题

消融实验

关于编码器的消融

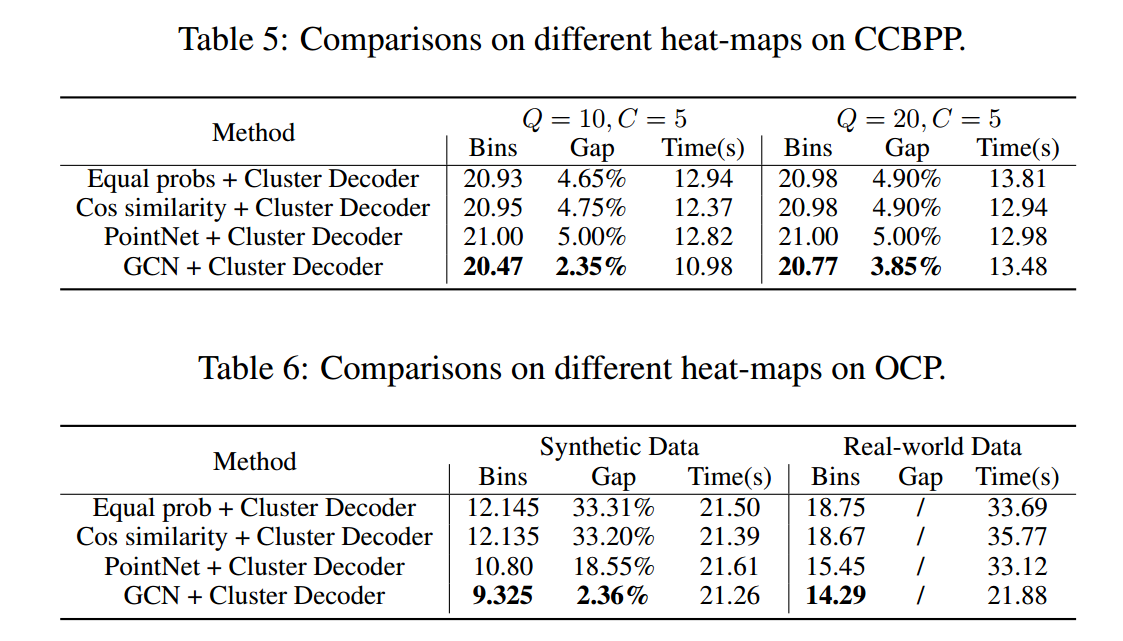
聚类解码算法的消融

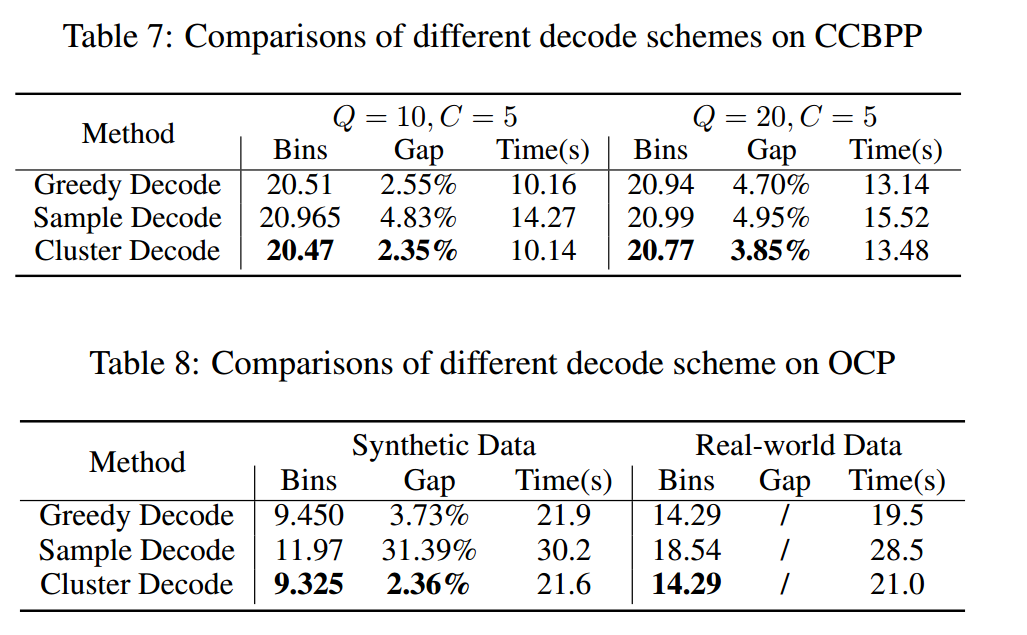
迭代次数的影响

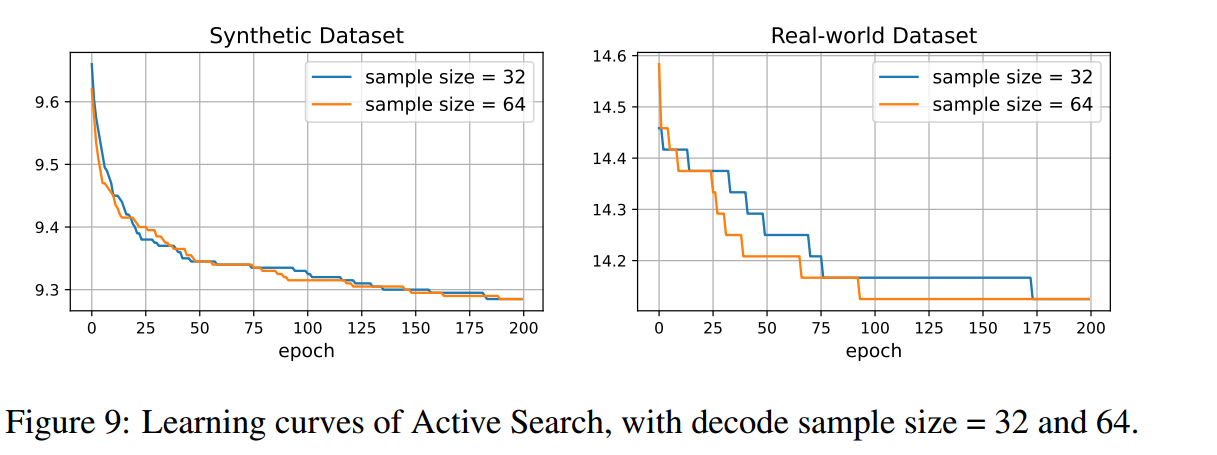
当样本量为32时，每个实例的运行时间接近90秒，当样本量为64时，每个实例的运行时间接近180秒，这在真实场景中有时是不可行的。该算法在实际应用中可能需要在求解质量和运行时间之间做出妥协。

总结

未来研究：

尝试提高我们的算法对不同规模和分布的CCBPP的通用性。
将模型应用到CCBPP的其他应用中。

Learning to Solve Class-Constrained Bin Packing Problems via Encoder-Decoder Model

ICLR2024 热图装箱问题

摘要

介绍

相关工作