ICAM: Rethinking Instance-Conditioned Adaptation in Neural Vehicle Routing Solver
ICLR 2025 under review
摘要
神经组合优化(NCO)方法在不需要专家知识的情况下解决路由问题显示出巨大的潜力。然而,现有的建设性NCO方法仍然难以解决大规模实例,这大大限制了它们的应用前景。为了解决这些关键的缺点,这项工作提出了一种新的实例条件适应模型(ICAM),以更好地大规模泛化神经路由求解器。特别地,我们设计了一个简单而高效的实例条件自适应函数,以较小的时间和内存开销显著提高了现有NCO模型的泛化性能。此外,通过对不同注意机制之间信息融合性能的系统研究,我们进一步提出了一个功能强大但低复杂度的实例条件适应模块,以生成更好的解决方案。实验结果表明,该方法在求解旅行商问题(TSP)、有能力车辆路径问题(CVRPs)和非对称旅行商问题(ATSP)时,能够以非常快的推理时间获得令人满意的结果。据我们所知,我们的模型在所有基于rl的构造方法中达到了最先进的性能,用于多达1000个节点的TSP和ATSP,并将最先进的性能扩展到CVRP实例上的5000个节点,并且我们的方法也可以很好地泛化以解决交叉分布实例。
介绍
贡献:
- 设计了一个简单而高效的实例条件自适应函数,以较小的时间和内存开销显著提高现有NCO模型的泛化性能。
- 系统地研究了不同注意机制在整合信息方面的差异,然后进一步提出了一个功能强大但低复杂度的实例条件自适应模块,以获得更好的泛化性能。
- 对不同的问题进行了各种实验,以证明ICAM可以以非常快的推理时间为跨尺度实例生成有希望的解决方案。据我们所知,它在所有基于rl的构造方法中实现了最先进的性能,用于多达1,000个节点的tsp和atsp,并将最先进的性能扩展到CVRP实例上的5,000个节点。
相关工作
- 无条件NCO
- POMO + beam search \ MCTS \ 主动搜索
- 两阶段方法
- Learning collaborative policies to solve np-hard routing problems.
- Generalize learned heuristics to solve large-scale vehicle routing problems in real-time.
- Learning to delegate for large-scale vehicle routing.
- Glop: Learning global partition and local construction for solving large-scale routing problems in real-time.
- 缺点:依赖专家知识
- 扩大规模训练NCO
- Neural combinatorial optimization with heavy decoder: Toward large scale generalization.
- BQ-NCO
- 基于辅助信息的NCO
- 结合距离信息
特定于实例的模式
动机和关键思想
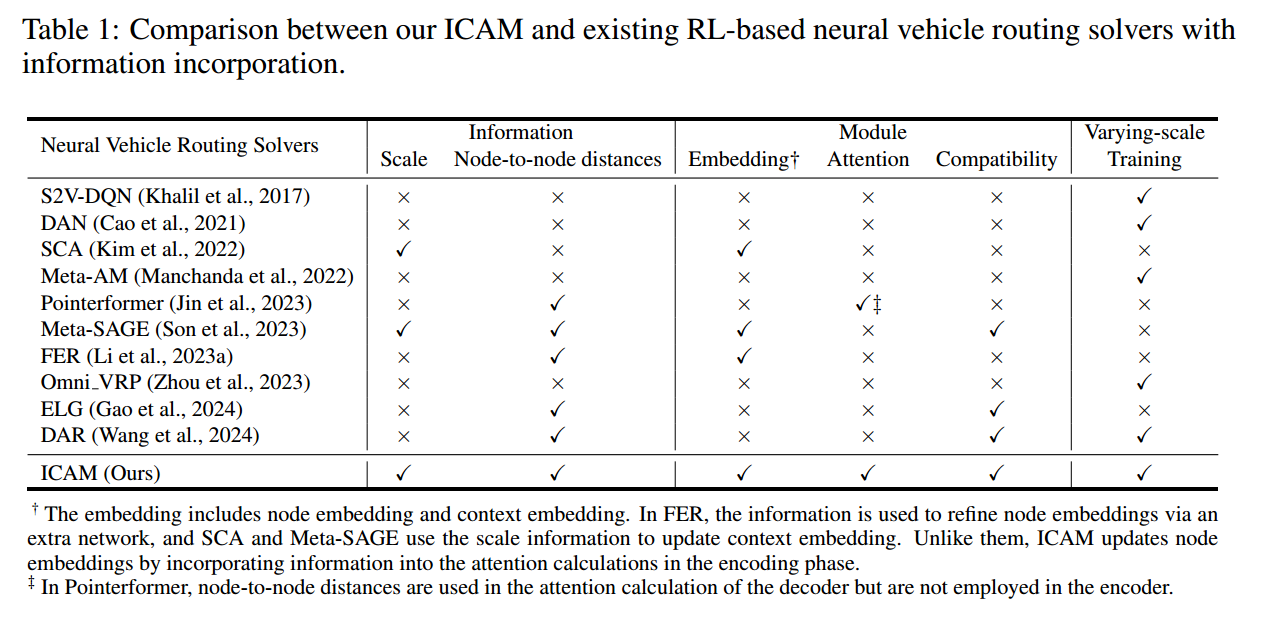
如表中所示,三个方面很重要
- 全面的实例条件信息:仅使用点到点的距离或者尺度信息是不够的,整体使用实例信息对泛化性能很重要。
- 多模块集成:包括 embedding、attention、compatibility
- 扩大训练规模
特定于实例的适应函数
一个简单有效的实例条件适应函数 $f(N,d_{ij})$
\[f(N,d_{ij})=-\alpha\cdot \log_2 N\cdot d_{ij},\forall i,j\in 1,\cdots,N,\]其中 $N$ 是问题规模,$d_{ij}$ 是节点距离,$\alpha$ 是可学习的参数。取对数是避免在大规模中函数值过大,距离越近适应值分数越高。
函数优势:
- 利用了全面的实例条件信息
- 参数只有一个,减少时间和内存开销,该函数使模型在面对大规模实例时保持高效率
为了证明函数的有效性进行了如下实验
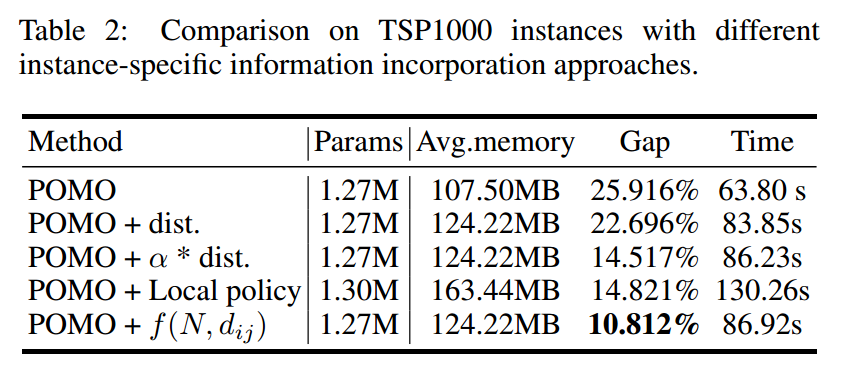
具体的添加方式为,在编码器中
\[\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}}+G)V\]这个 $G=\lbrace g_{ij}\rbrace$ 就是添加的信息。
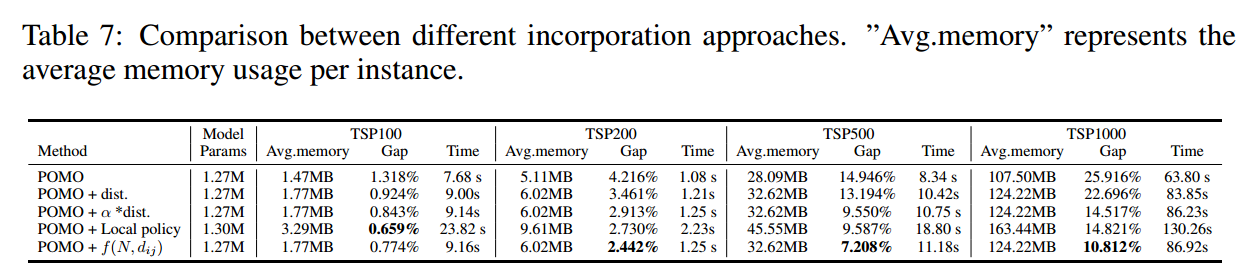
模型
重新审视 AM 机制
MHA 的时空复杂度都很高,而且不利于捕捉节点之间的关系,不能直接利用节点之间的距离。
Adaptation Attention Free Module
提出了如下计算方式
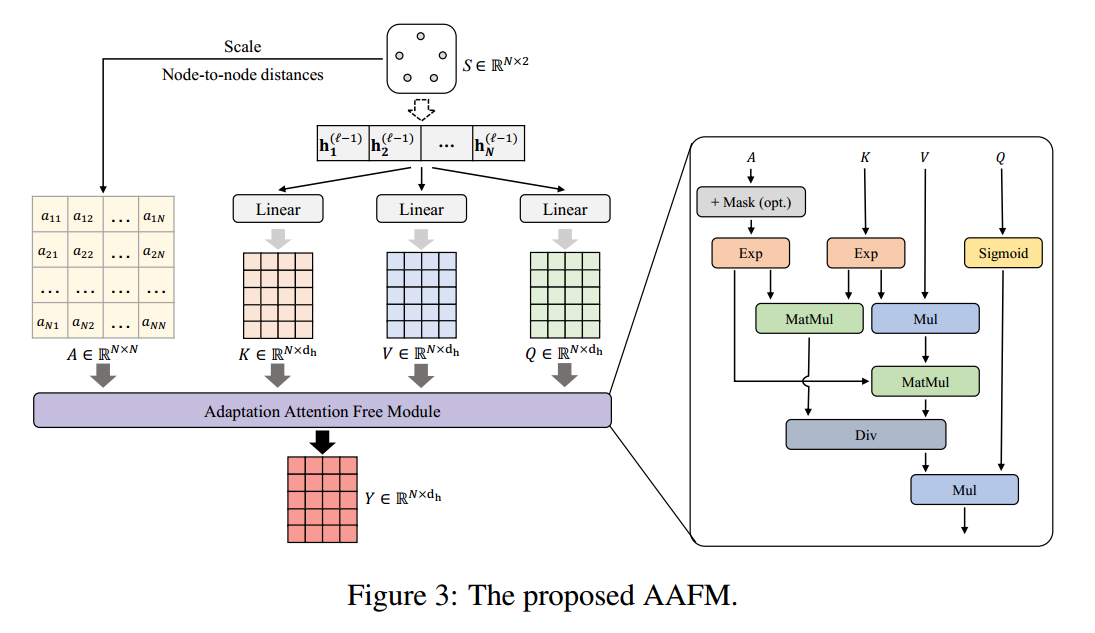
这里的 $A$ 就是上文提到的 $f(N,d_{ij})$。优势是复杂度比 MHA 更低。计算公式为
\[\text{AAFM}(Q,K,V,A)=\sigma(Q)\odot \frac{\exp(A)\cdot (\exp(K)\odot V)}{\exp(A)\cdot \exp(K)}\]这种方法的起源是《An attention free transformer.》提出的 AFT,就上式没有 $A$ 就是 AFT了。AFT 的优势如下,
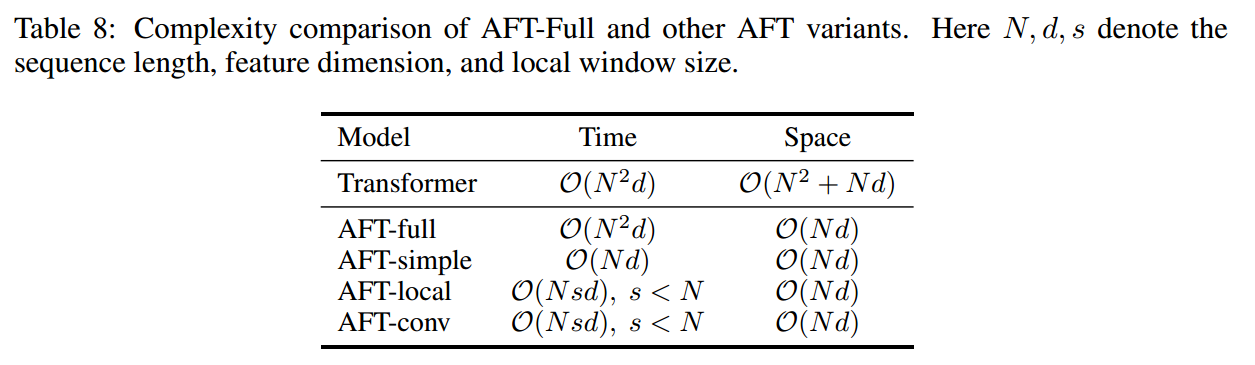
从性能角度来看,AFT 是不如 MHA 的。但在路由问题中不一定,因为 MHA 不能利用节点距离信息,而 AFT 可以。实验结果表明确实如此
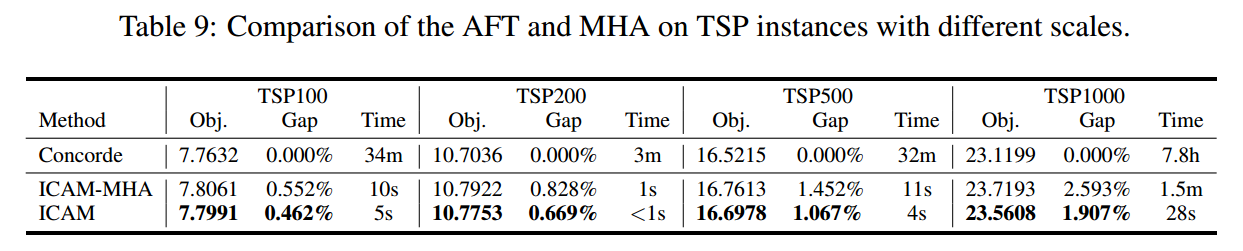
带有 Adaptation Bias 的 Compatibility
为了进一步提高求解性能,将 $f\left(N, d_{i j}\right)$ 整合到Compatibility计算中。新的Compatibility $u_i^t$ 可以表示为
\[\begin{gathered} u_i^t= \begin{cases}\xi \cdot \tanh \left(\frac{\hat{\mathbf{h}}_{(C)}^t\left(\mathbf{h}_i^{(L)}\right)^{\mathrm{T}}}{\sqrt{d_k}}+a_{t-1, i}\right) & \text { if } i \notin\left\{\pi_{1: t-1}\right\} \\ -\infty & \text { otherwise }\end{cases} \\ p_{\boldsymbol{\theta}}\left(\pi_t=i \mid S, \pi_{1: t-1}\right)=\frac{e^{u_i^t}}{\sum_{j=1}^N e^{u_j^t}} \end{gathered}\]其中,$\xi$ 是裁剪参数,$\hat{\mathbf{h}}_{(C)}^t$ 和 $\mathbf{h}_i^{(L)}$ 是通过 AAFM 计算的(前者是 $\hat{\mathbf{h}}_{(C)}^t=[\mathbf{h}_{\pi_1}^{(L)},\mathbf{h}_{\pi_{t-1}}^{(L)}]$),而不是通过 MHA。$a_{t-1, i}$ 表示每个剩余节点与当前节点之间的适应偏差。
实验
单个 24GB 的 3090。
ATSP 用 MatNet。
三阶段训练:
-
小规模上热身,TSP100。TSP的batch是256,ATSP是128,CVRP容量固定为50。
-
在不同规模上学习。问题规模从 [100, 500] 上采样。(A)TSP的batch调整为 $bs=[160\times (100/N)^2]$,CVRP 调整为 $bs=[128\times (100/N)^2]$。
-
Top-k 训练。关注所有 $N$ 个轨迹中最好的 $k$ 个。损失修改为 $\mathcal{L}_{\text{Joint}}=\mathcal{L}_{\text{POMO}}+\beta\mathcal{L}_{\text{Top}}$,$k$ 设置为 20。
具体计算:
在第一和第二阶段中使用的损失函数(记作 $\mathcal{L}_{\mathrm{POMO}}$)与 POMO 中的相同。POMO 通过 REINFORCE进行训练,并使用近似梯度上升。损失函数的近似梯度上升可以写为
\[\begin{gathered} \nabla_\theta \mathcal{L}_{\mathrm{POMO}}(\theta) \approx \frac{1}{B N} \sum_{m=1}^B \sum_{i=1}^N R\left(\pi^i \mid S_m\right)-b^i\left(S_m\right) \nabla_\theta \log p_\theta\left(\pi^i \mid S_m\right), \\ b^i\left(S_m\right)=\frac{1}{N} \sum_{j=1}^N R\left(\pi^j \mid S_m\right) \quad \text { 对所有 } i \end{gathered}\]其中,$R\left(\pi^i \mid S_m\right)$ 表示给定特定解 $\pi^i$ 的实例 $S_m$ 的总奖励(例如,路径长度的负值)。
在第三阶段,模型更加关注所有 $N$ 条轨迹中的最佳 $k$ 条轨迹。为此,设计了新的损失 $\mathcal{L}_{\text {Top }}$,其梯度上升可以表示为
\[\nabla_\theta \mathcal{L}_{\mathrm{Top}}(\theta) \approx \frac{1}{B k} \sum_{m=1}^B \sum_{i=1}^k R\left(\pi^i \mid S_m\right)-b^i\left(S_m\right) \nabla_\theta \log p_\theta\left(\pi^i \mid S_m\right)\]
实验结果
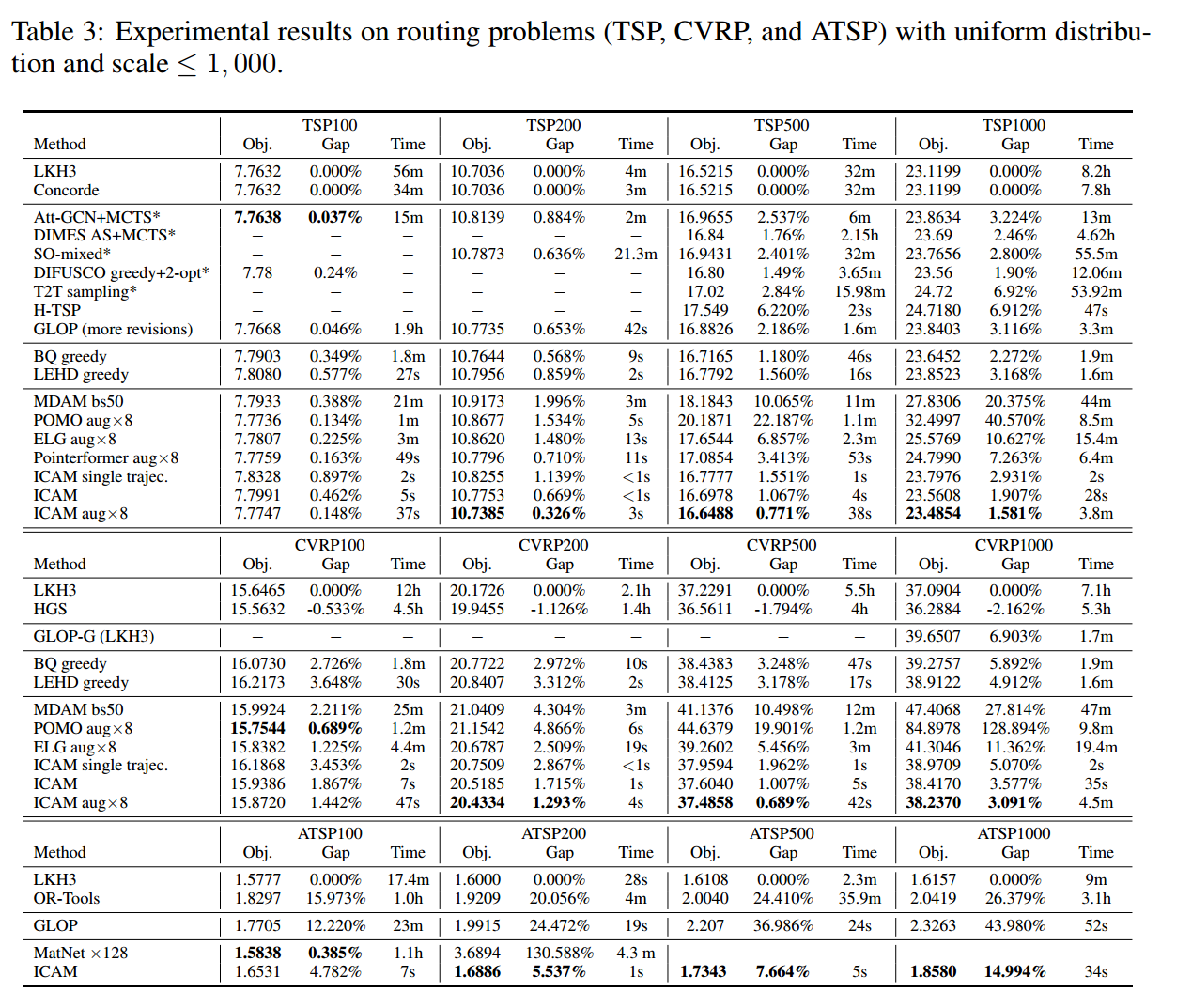
不同分布(旋转和爆炸)
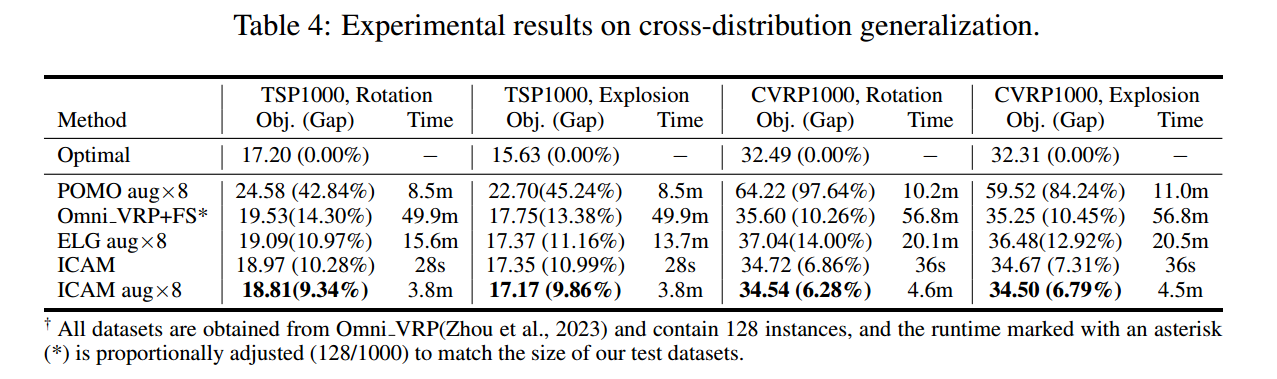
更大的规模
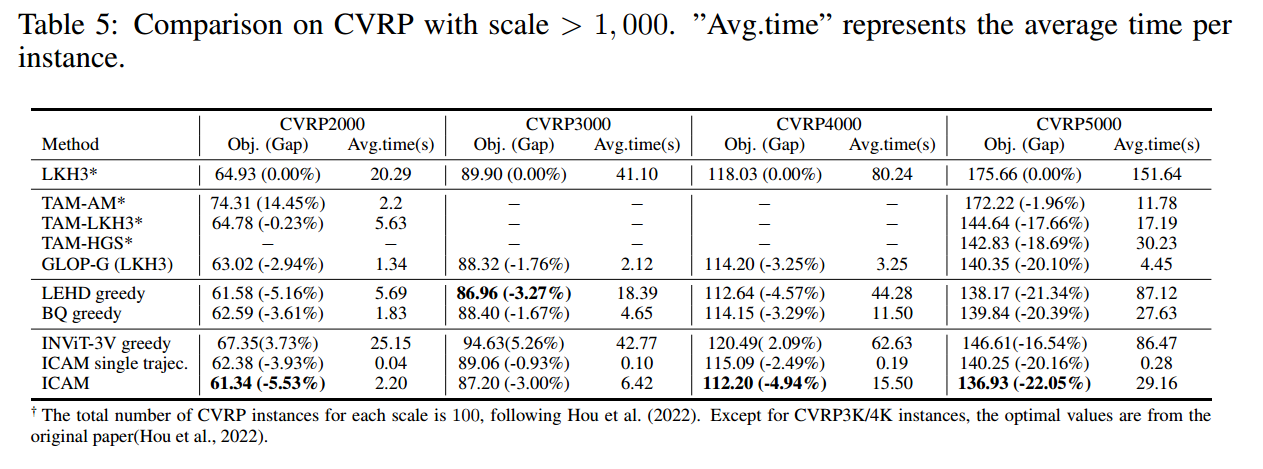
benchmark
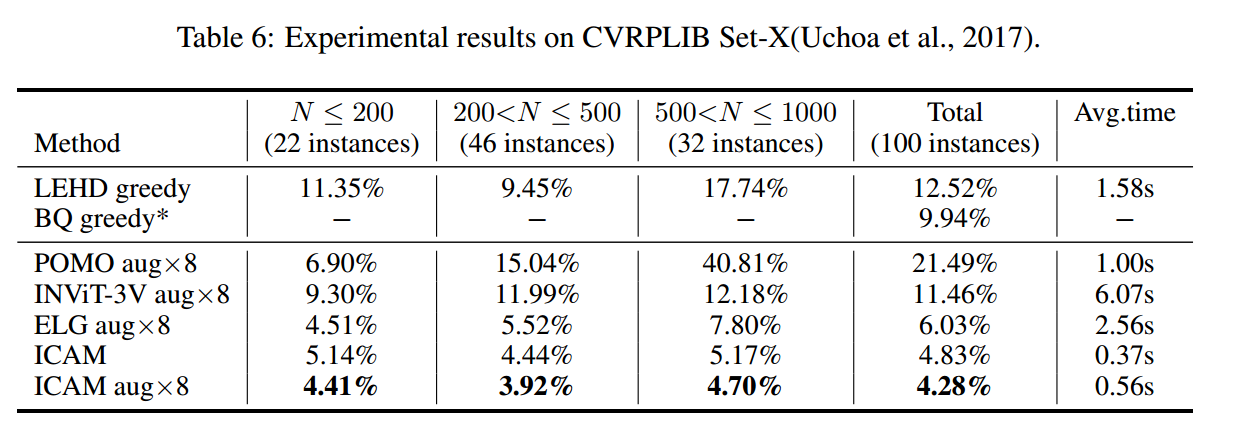
消融实验
适应函数组成部分的影响
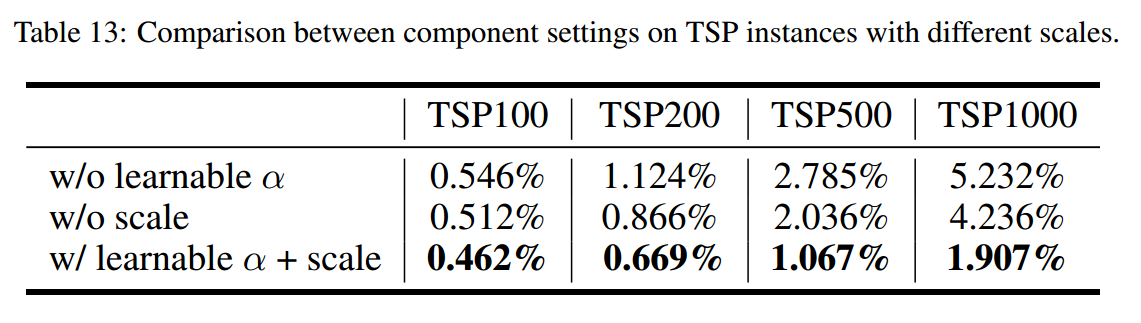
适应函数的影响
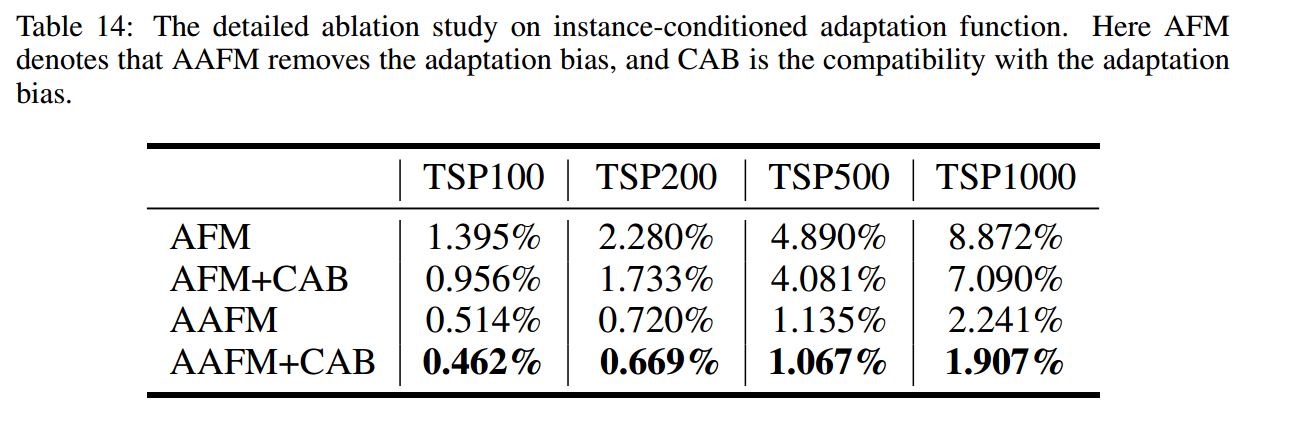
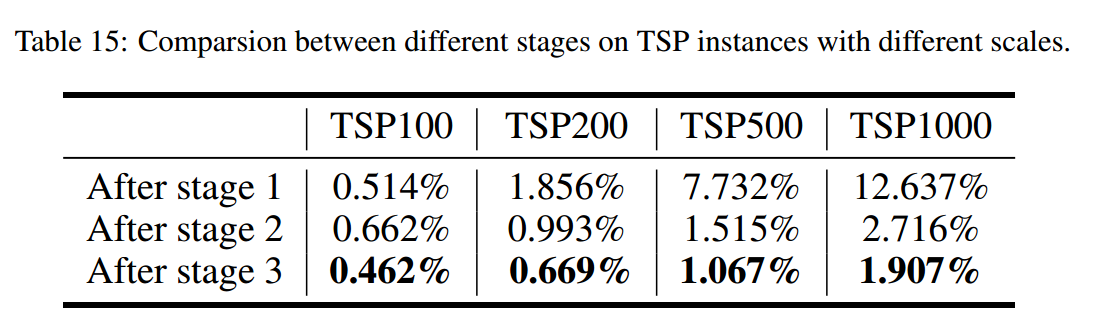
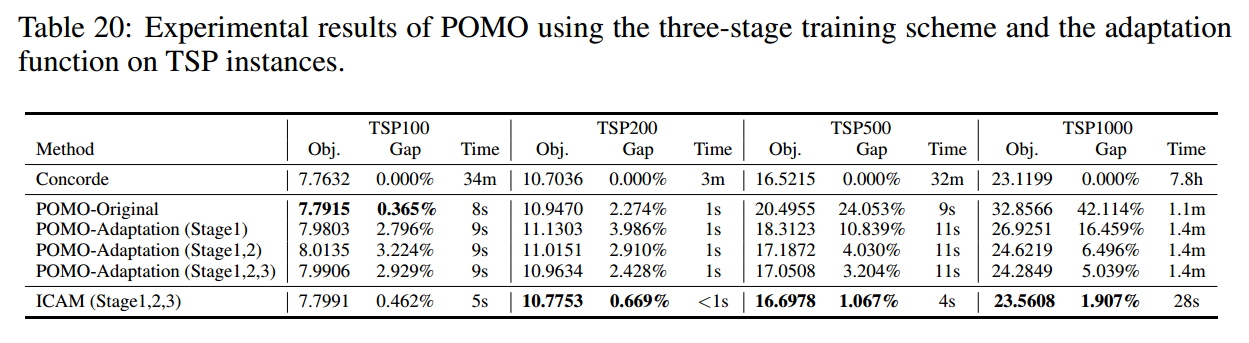
不同阶段的影响
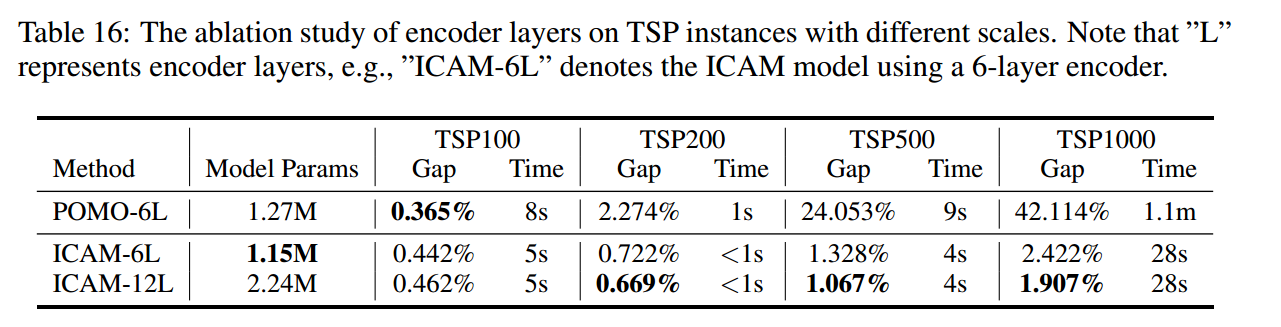
深度编码器的效果
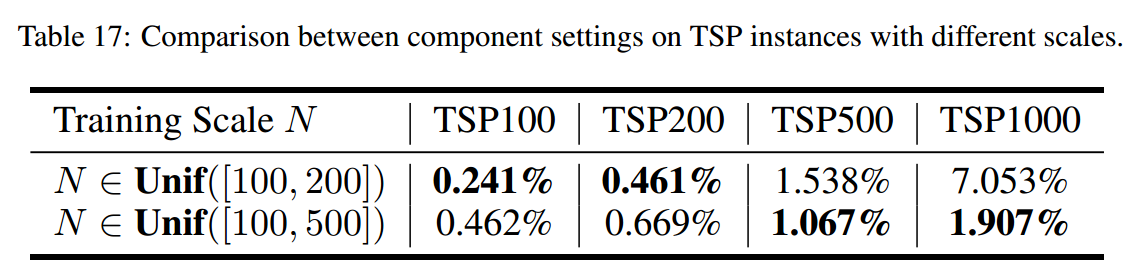
较大培训规模的影响
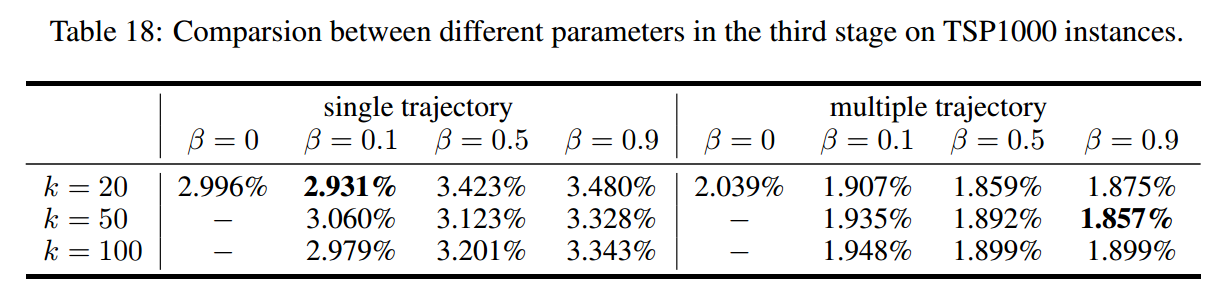
第三阶段参数设置
ICAM与POMO的三阶段训练计划
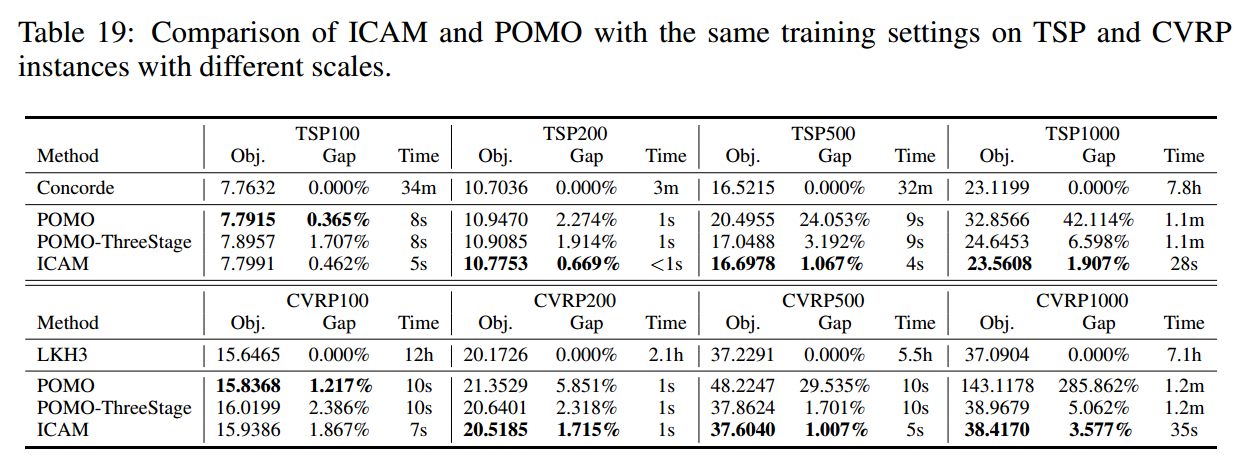
POMO适应性能
复杂性分析

总结
ICAM 在 greedy 解码的适合表现较好,但在 beam search 和 RPC 解码的时候适应性较差。