Learning to Handle Complex Constraints for Vehicle Routing Problems

Learning to Handle Complex Constraints for Vehicle Routing Problems

学习处理车辆路线问题的复杂约束

南洋理工大学，ASTAR

摘要

车辆路径问题（vrp）可以模拟许多现实场景，并且通常涉及复杂的约束。虽然最近的神经方法在构建基于可行性掩蔽的解决方案方面表现出色，但它们难以处理复杂的约束，特别是当获得掩蔽本身是NP-hard时。在本文中，提出了一个新的主动不可行性预防（PIP）框架，以推进神经方法在更复杂的vrp中的能力。的PIP集成了拉格朗日乘子作为基础，以增强约束意识，并引入了预防性的不可行性掩蔽，以主动引导解决方案的构建过程。此外，提出了PIP-D，它使用一个辅助解码器和两种自适应策略来学习和预测这些定制的掩码，潜在地提高了性能，同时显著降低了训练期间的计算成本。为了验证的PIP设计，在不同约束硬度水平下对极具挑战性的带时间窗的旅行商问题（TSPTW）和带草图限制（TSPDL）变体的旅行商问题（TSP）进行了大量实验。值得注意的是，的PIP 是通用的，可以增强许多神经方法，并且显着降低了不可行率，并显着提高了解质量。

介绍

贡献：

1. 从概念上讲，展示了解决和推进vrp中复杂相互依赖约束的处理的早期工作，其中掩蔽机制由于上述困境而失去有效性，从而将神经方法的应用扩展到更实际的场景。
2. 在方法上，提出了新的PIP和PIP- d方法，可以提高大多数建设性神经方法的能力。具体来说，利用拉格朗日乘法器方法并引入预防性不可行性掩蔽，通过具有两种自适应策略的辅助解码器网络进一步学习，在解构建过程中主动有效地引导搜索。
3. 实验上，进行了广泛的验证，以证明PIP在各种骨干模型（即AM， POMO和GFACS）和复杂VRP变体（即TSPTW和TSPDL）中的有效性和多功能性。值得注意的是，PIP 在不同约束硬度水平的合成和基准数据集上实现了不可行率的显著降低（高达93.52%）和解质量的显著改善。

方法论

可行性mask困境

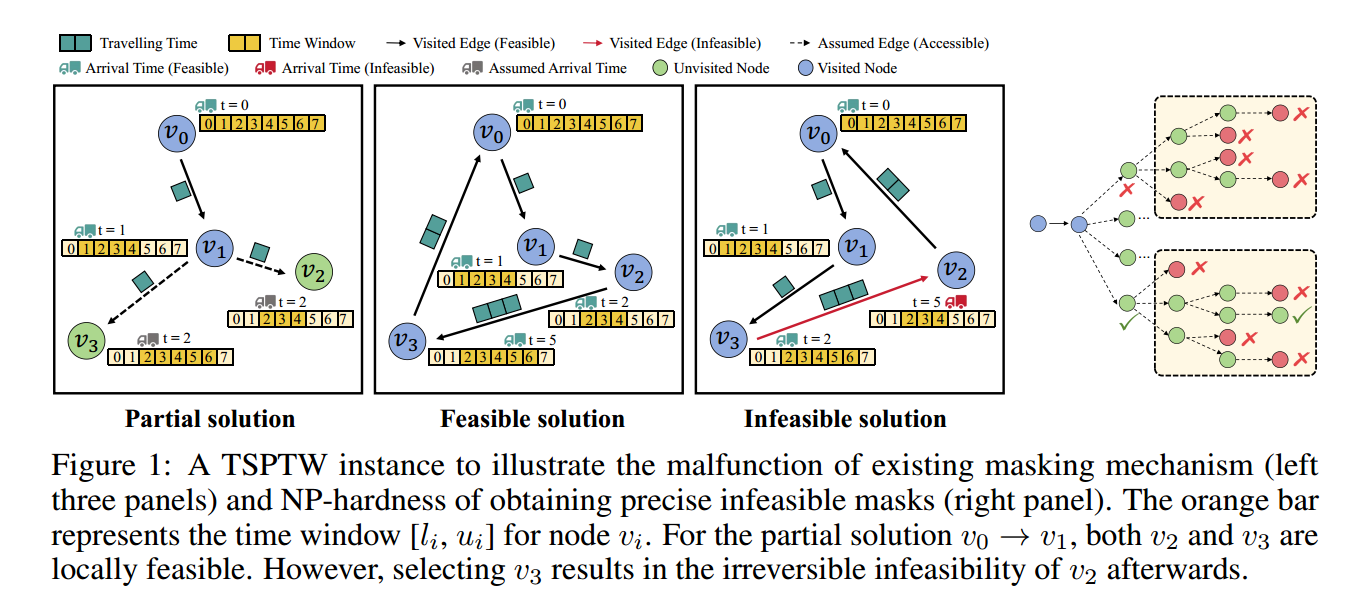
只考虑局部可行性并不能保证整体可行性，可能导致不可逆的不可行性，如图3。

一种潜在的补救方法是计算考虑所有未来可能性的全局可行性掩码，如图1，但这样计算mask又变成了一个NP问题。

这种mask困境在TSP类问题中表现明显，VRP类稍有缓解。

由PIP指导策略搜索

首先将车辆路径规划（VRP）的解决方案构建过程公式化为一个受限马尔可夫决策过程（CMDP），其由元组 $(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \mathcal{C})$ 定义，其中 $\mathcal{S}$ 是状态空间，$\mathcal{A}$ 是从节点 $v_i$ 到节点 $v_j$ 的动作空间，$\mathcal{R}: \mathcal{S} \times \mathcal{A} \times \mathcal{S}$ 是奖励函数，$\mathcal{C}: \mathcal{S} \times \mathcal{A} \times \mathcal{S}$ 是约束违反成本（惩罚）函数，$\mathcal{P}: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow[0,1]$ 是转移概率函数。在每个时间步，神经解算器输出所有候选节点的概率，并选择一个节点以构建完整的解决方案 $\tau$。CMDP 的目标是学习一个策略 $\pi_\theta: \mathcal{S} \rightarrow \mathcal{P}(\mathcal{A})$，以最大化在某些约束条件下的状态奖励总和，

其中 $\mathcal{J}$ 是策略的期望回报，$\Pi_F$ 表示所有可行策略的集合，$\kappa_m$ 代表不等式约束 $\mathcal{C}_m$ 的边界，$M$ 是约束的数量。具体而言，可行策略 $\pi$ 是指其相对于 $\mathcal{C}_m$ 的约束违反的期望值 $\mathcal{J}_{\mathcal{C}_m}(\pi)$ 不超过 $\kappa_m$。注意，本文中 $\kappa_m$ 设置为 0，因为考虑的是不容忍任何违反的硬约束。此外，将奖励函数 $\mathcal{R}$ 设置为两个节点之间欧几里得距离的负值，即 $\mathcal{R}\left(e\left(v_i, v_j\right)\right)=-\mid v_i-v_j\mid _2$。通过应用可行性掩码，搜索仅限于可行区域，使神经方法能够专注于公式 (2) 中的目标函数，而不必明确考虑约束意识或约束违反。然而，当这些掩码不可用时，这些方法的有效性会下降，从而导致在大规模不可行区域中的低效搜索。为了解决这个问题，提出了 PIP，结合约束感知的拉格朗日乘子和预防性不可行性屏蔽，将复杂约束问题的搜索空间限制在近可行区域。

拉格朗日辅助的约束意识

设计了一种基于拉格朗日乘子的算法，将约束 $\mathcal{C}$ 纳入奖励函数 $\mathcal{R}$ 中。根据拉格朗日乘子定理，公式 (2) 中的 CMDP 表述被转换为以下车辆路径规划（VRP）的马尔可夫决策过程（MDP）表述：

其中 $\mathcal{L}$ 是拉格朗日函数，$\lambda_m$ 是一个非负的拉格朗日乘子。一般来说，约束违反项计算为所有约束的总违反值。在时间窗旅行商问题（TSPTW）中，$\mathcal{J}_{\mathrm{TW}}(\tau)=\sum_{i=0}^n \max \left(t_i-u_i, 0\right)$，而在时间窗有时间限制的旅行商问题（TSPDL）中，$\mathcal{J}_{\mathrm{DL}}(\tau)=\sum_{i=0}^n \max \left(\alpha_i-d_i, 0\right)$。除此之外，引入了解决方案 $\tau$ 中不可行节点的数量，称为 $\mathcal{J}_{\text {IN }}$，作为拉格朗日函数中的额外项，以增强约束意识，这在经验上被发现有效地减少了不可行率。虽然在针对软目标的神经迭代方法中已经探索了拉格朗日松弛，但的方法引入了专门为神经构造方法量身定制的约束违反成本函数，并考虑固定拉格朗日乘子 $\lambda$（对偶变量）并优化原变量 $\theta$，显著减少了计算开销。

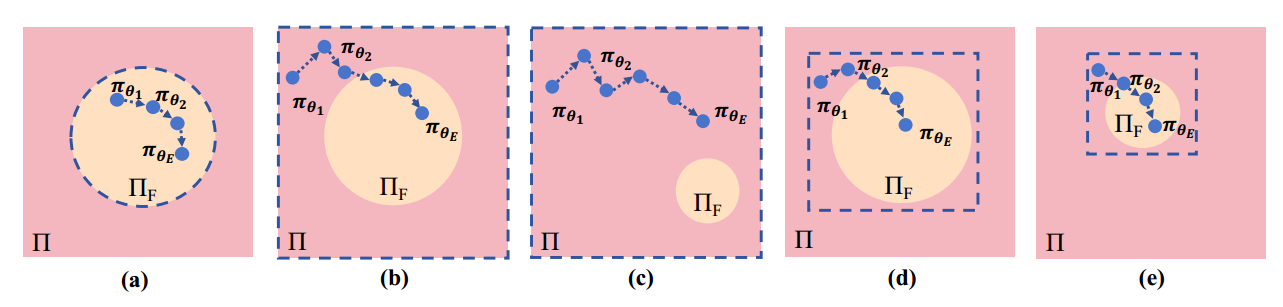
图2：不同难度级别(a)(b)(d)简单和(c)(e)困难的VRP上的政策优化轨迹说明，以及不同的约束处理方案——(a)可行性掩蔽，(b)(c)拉格朗日乘子，(d)(e)我们的PIP。橙色填充的圆圈表示可行策略空间ΠF，虚线框表示神经策略的实际搜索空间πθ。

预防性不可行性（PI）掩码

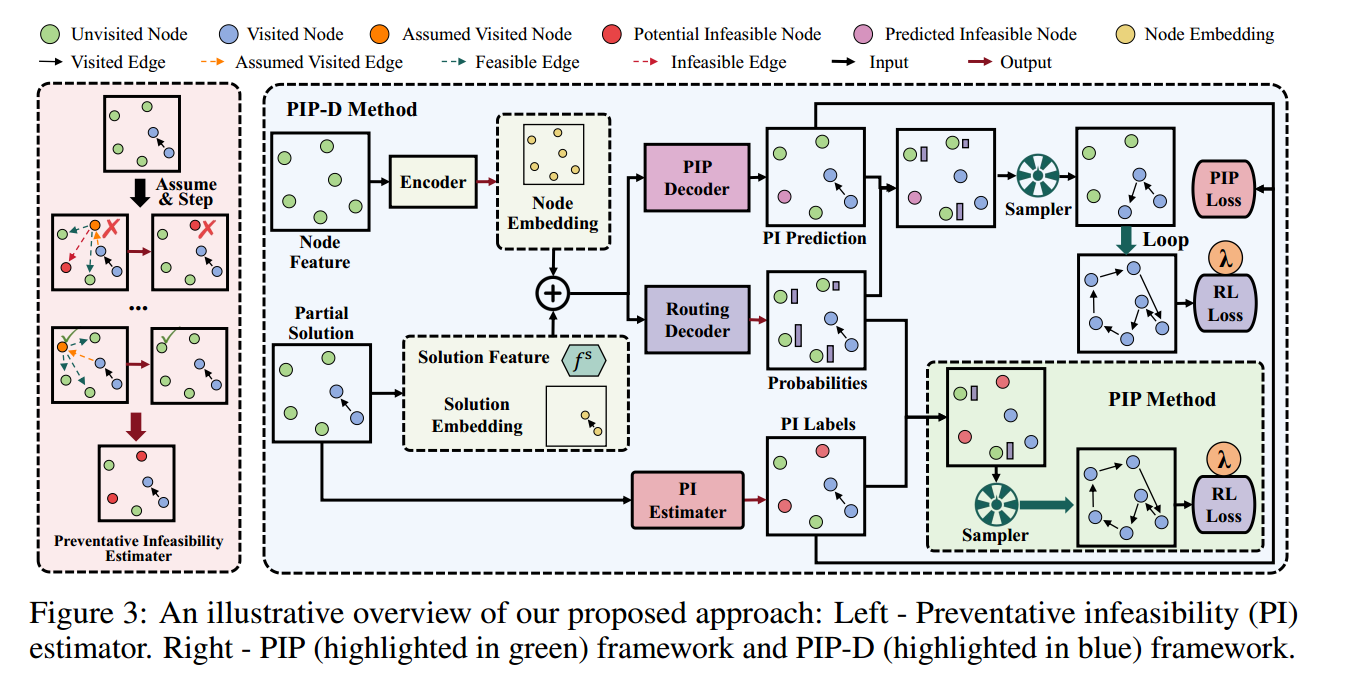
正如图 2(b) 所示，定制的拉格朗日乘子通过公式 (3) 引导神经策略朝向潜在的可行和高质量的空间。然而，对于图 2(c) 中展示的更复杂情况，神经解算器可能仍然难以在大的搜索空间中进行导航。为进一步提高训练效率和解决方案的可行性，引入预防性不可行性（PI）掩码，以主动避免在解决方案构建过程中选择不可行节点。如图 3 左侧面板所示，如果选择某个候选节点（例如橙色节点）导致其他候选节点（例如绿色节点）由于约束违反而在下一步变得潜在不可访问，则该节点被标记为不可行（即红色节点），因为选择它会导致不可逆转的未来不可行性（详细示例见附录 A.3）。需要注意的是，本文采用了一种简单而有效的一步 PI 掩码，以平衡计算成本，而不必遍历所有未来可能性（这在计算上是 NP-hard 的）。结合定制的拉格朗日乘子，的 PIP 主动将搜索空间减少到一个接近可行的域 $\Pi_{\widetilde{F}}$，如图 2(d)-(e) 所示。值得注意的是，这种 PIP 设计是通用的，可以应用于增强大多数具有复杂相互依赖约束的 VRP 神经构造解算器。

学会避免不可行性

获取上述PI信息会引入额外的计算成本。为了缓解这一问题，提出了一个辅助解码器网络来学习和预测这些掩码，用PIP解码器更快的前向传递取代生成PI信息的耗时过程。这进一步加快了训练过程，形成了PIP框架的增强版本，称为PIP- d。

辅助PIP解码器

上层网络用于寻找路由，下层网络用于预测mask。

PIP-D 训练与自适应策略

尽管如此，高效地训练 PIP 解码器和路由解码器需要有效的设计。通过两种自适应策略来解决这个问题。首先，在每个梯度步骤中训练 PIP 解码器会导致比原始 PIP 更高的计算复杂度，这与降低训练复杂度的目标相悖。

因此，采用周期性更新策略，间歇性地更新 PIP 解码器，而不是持续进行更新。这个方法基于一个观察，即神经网络推荐的 PI 掩码在短训练周期内通常保持稳健。具体来说，首先用 $E_{\text {init }}$ 个周期训练 PIP 解码器，然后每 $E_p$ 个周期周期性地更新 $E_u$ 个周期，最后进行 $E_l$ 个周期的更新。通过这种方式，计算成本得以降低，并可以自适应调整。

其次，考虑对具有不同固有难度的实例平衡可行和不可行的 PI 信号。鉴于不同 VRP 变体中可行和不可行节点的 PI 信号比例可能会显著不同，采用加权平衡策略来减轻标签不平衡的影响 ，其公式如下：

其中 $T$ 是构建完整解决方案的总解码步骤。每个类别的权重通过其对应的样本数量计算，即 $\omega_{\text {infsb }}=\frac{N_{\text {infs }}+N_{\text {fsb }}}{2 N_{\text {infs }}}, \omega_{\mathrm{fsb}}=\frac{N_{\text {infs }}+N_{\text {fsb }}}{2 N_{\mathrm{fsb}}}$，其中 $N_{\text {infs }}$ 和 $N_{\mathrm{fsb}}$ 分别是在特定解码步骤 $t$ 中通过 PI 掩码 $\left(g_t\right)$ 识别的可行和不可行节点的数量。

此外，除了上述两种关键策略外，还探索了其他策略以加速 PIP 解码器的训练，包括微调和早停技术。

实验

Sol. 表示训练过程中的不可行率，Inst. 表示评估时候的不可行率，Gap 表示和LKH的gap。

对于TSPTW，通过调整时间窗口的宽度和重叠来生成三种类型的实例：简单、中等和困难。

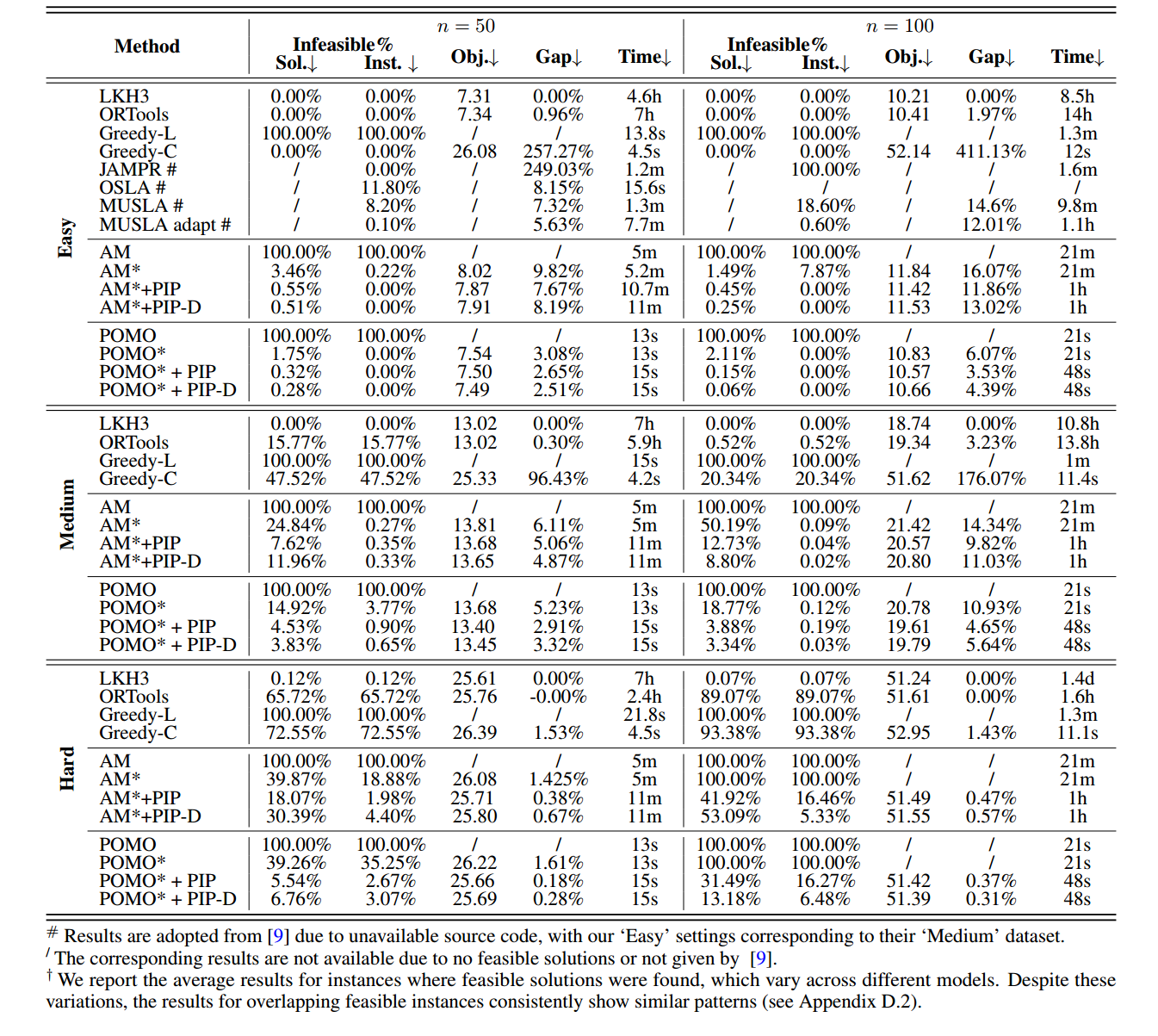
对于TSPDL，我虑了两个硬度级别：中等和困难。

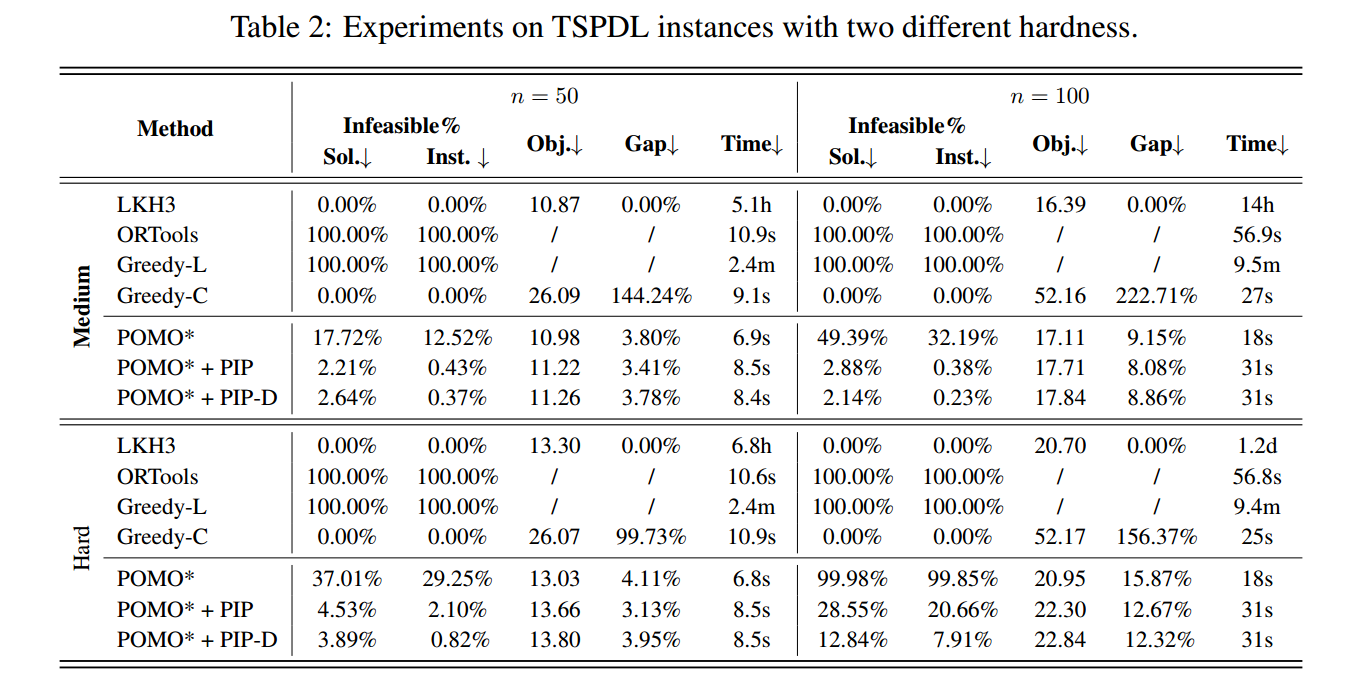
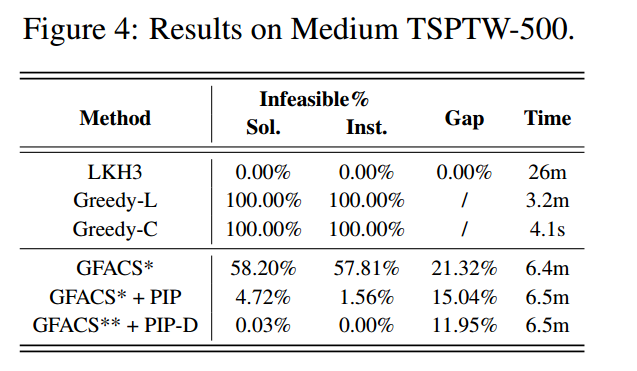
大规模实验

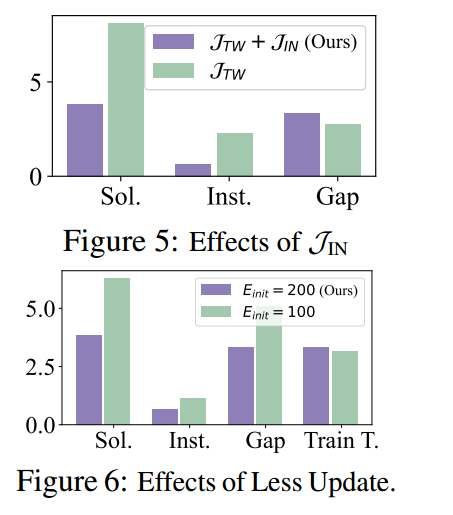
消融实验

• PIP 和 PIP-d
• 拉格朗日方程中的项
• 加权平衡策略
• 周期更新策略

总结

未来方向：

1. 将PIP应用于更大规模的更多神经方法
2. 将PIP扩展到神经迭代求解器
3. 将PIP应用于具有复杂约束的更多VRP变体，包括那些由现有掩蔽机制可求解但具有较大最优性差距的硬约束 VRP

• Previous
  ICAM Rethinking Instance-Conditioned Adaptation in Neural Vehicle Routing Solver
• Next
  基于 Saving 算法求解路径规划问题