Saving 方法
Clarke and Wright Saving算法
Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 1964
- 计算 $S_{ij}=d_{i0}+d_{0j}-d_{ij}$
- 将所有 $S_{ij}$ 加入优先队列,大的值优先
- 每一轮取队头的 $(i,j)$
- 如果 $i,j$ 都是单个节点的路径,则合并
- 如果 $i$ 是单个节点的路径,$j$ 在某一条路径的开始或者结束,则合并
- 如果 $i,j$ 各自在某一条路径中,但都在路径的开始或者结束,则合并
- 否则,不操作
缺点:大规模的时候精度不行
方法改进
多个标准 一些综述
A fuzzy multi-criteria approach based on Clarke and Wright savings algorithm for vehicle routing problem in humanitarian aid distribution
Journal of Intelligent Manufacturing (2023)
土耳其 Sakarya University
综述
- $S_{ij}=C_{i0}+C_{0j}-\lambda C_{ij}$
- $c_{ik}^{mod}=\min_m(c_{im})-(c_{ik}-\min_m(c_{im}))$,多仓库,$k$ 是仓库,$i$ 是客户
- $S_{ij}=C_{i0}+C_{0j}-\lambda C_{ij}+\mu\mid C_{0i}-C_{j0}\mid $
- $S_{ij}=C_{i0}+C_{0j}-\lambda C_{ij}+\mu\mid C_{0i}-C_{j0}\mid +v(d_i+d_j)/\bar{d}$,其中 $d$ 是需求
本文提出的方法
- $S_{ij}=(C_{i0}+C_{0j}-C_{ij})\times IC_{ij}$,$IC_{ij}$ 是重要性系数,需要复杂的计算
域规约 减少规模
An Improved Clarke and Wright Algorithm to Solve the Capacitated Vehicle Routing Problem
Engineering, Technology & Applied Science Research 2013
澳大利亚Curtin科技大学、科威特澳大利亚学院
问题:CVRP
- 删除一些较长的边以减小规模
蒙特卡洛模拟、分割技术、Saving 启发式结合
On the use of Monte Carlo simulation, cache and splitting techniques to improve the Clarke and Wright savings heuristics
Journal of the Operational Research Society (2011)
西班牙巴塞罗那加泰罗尼亚开放大学
The SR-GCWS hybrid algorithm for solving the capacitated vehicle routing problem
Applied Soft Computing 10 (2010)
西班牙巴塞罗那加泰罗尼亚开放大学
问题:CVRP
蒙特卡洛模拟:
- 基础的 saving 是贪婪构造的,即每次选择 saving 值最大的边合并,本文提出给每条边分配一个概率,该概率与 saving 值有关
- 从 $(0.05,0.25)$ 的均匀分布中随机选择一个值 $\alpha$,定义了特定的几何分布,该分布将用于根据每个符合条件的边在已排序的节省列表中的位置为其分配指数递减概率。这样,具有较高节省值的边总是更有可能从列表中被选择,但分配的确切概率是可变的。
- $P(X=k)=\alpha\cdot(1-\alpha)^{k-1}$
缓存机制:
- 蒙特卡洛模拟需要迭代完成,设计一个缓存机制,里面存储 best-known 的路由,即一组相同节点的最好的路由
- 每当发现包含完全相同的一组节点的更有效的路由时,该缓存就会不断更新
- 当找到相同的节点集合的新路由不好的时候,从缓存中替换
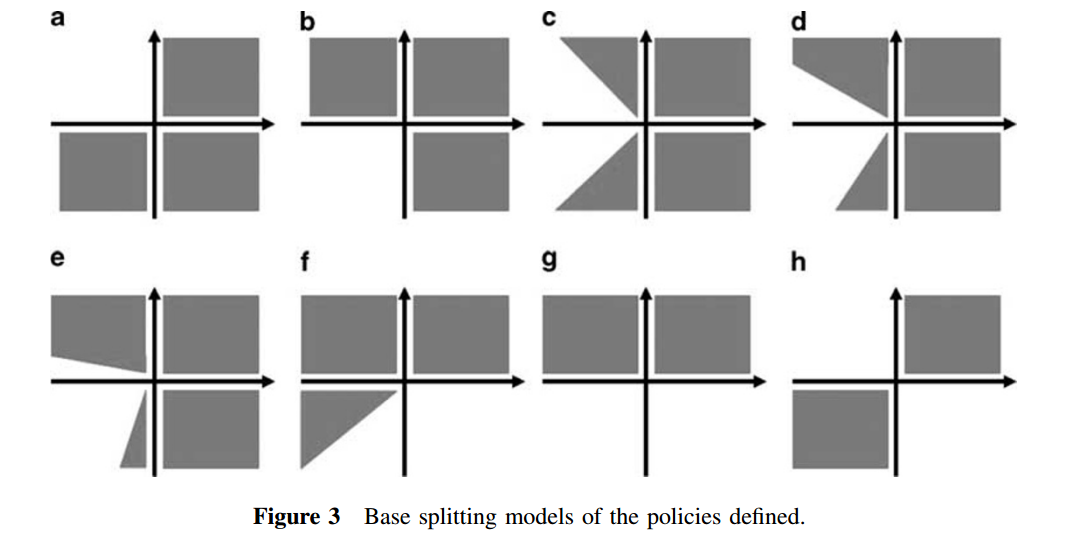
分割策略:
- 先将节点分治为若干块,然后分治执行带有缓存机制的蒙特卡洛模拟
- 56种分治策略,中心点是几何中心
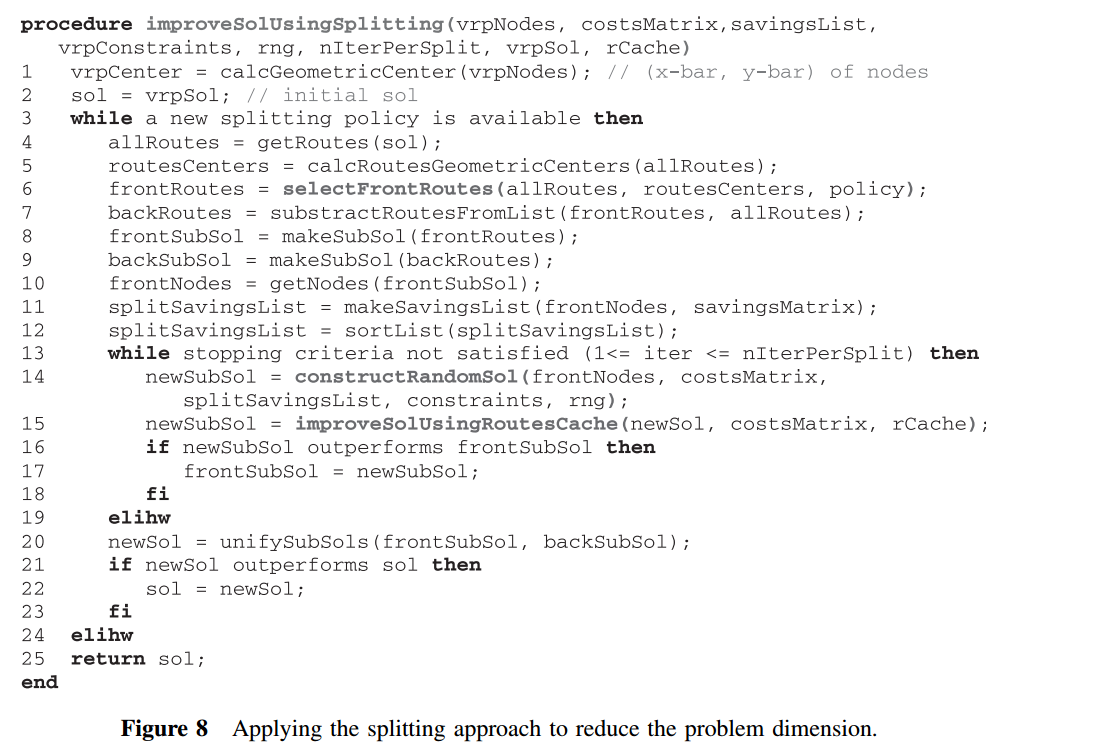
伪代码:




遗传算法
Tuning a Parametric Clarke-Wright Heuristic via a Genetic Algorithm
Journal of the Operational Research Society · November 2008
博洛尼亚大学
遗传算法 + saving
处理变种问题
VRPPD(VRP with Pickup and Delivery)
A new saving-based ant algorithm for the Vehicle Routing Problem with Simultaneous Pickup and Delivery
2010 Expert Systems with Applications
土耳其 Sabanci University
方法:saving-based ant algorithm
关注点:如何解决 Pickup and Delivery 约束
- 初始解
- 每条边 $\tau_i=1/nL_0$ 的信息素,$n$ 是节点数量,$L_0$ 是边长。
- saving 值改进为 $\phi_i=(d_{i0}+d_{0j}-d_{ij})/d_{ij}$,重点关注较近的节点对。这个值作为蚁群算法的可见度。
- 这个改进在 VRPPD 中是好的,但在 VRPTW 中是不好的。
- 蚁群算法选择下一个节点的吸引度为 $\tau_i^\alpha\cdot\phi_i^\beta$,softmax后按照 $\varepsilon$ - greedy 选择一个最大的。
- Local Search
- 重复 (i) Intra-Move, (ii) Intra-Swap, (iii) Inter-Move和(iv) Inter-Swap 直到无法改进
- Intra 表示路径内,Inter 表示路径间,move表示移动一个节点,swap表示交换两个节点。
MDVRPTW(Multi-depot VehicleRoutingProblemswith Time Windows)
A TabuSearch ApproachcombinedwithAn Extended Saving Methodfor Multi-depot Vehicle Routing Problems with Time Windows
2010 IJBSCHS
琉球大学
关注点:如何解决 Time Windows 约束
MDVRPTW 拆分为客户分配和路由问题。
- 客户分配用 Tabu Search
- 路由问题用 Saving,传统 Saving 只能考虑车辆的容量约束
- 车辆数量问题:saving 时,将车辆分配到包含更多客户的路线上。当两条路线上的顾客数量相同时,将车辆分配到路线总长度最小的路线上。
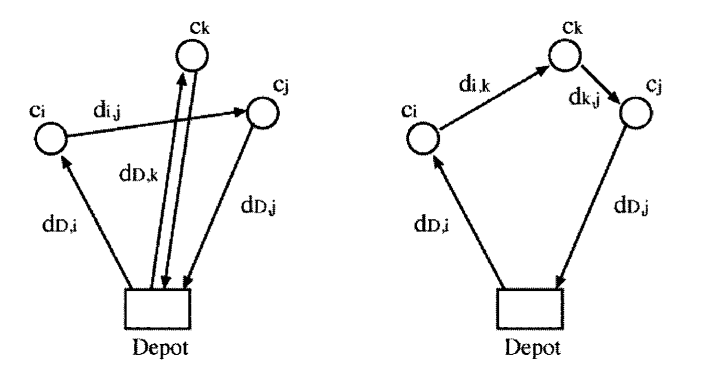
- 初始路线是每个节点分配的仓库的来回路线。
- 每次选择一个单个节点的路线,将其插入到其他路线当中,saving 值是插入任意节点间节省的路径长度。
- 最后需要移动节点改进。
VRPTW
A Three-Stage Saving-Based Heuristic for Vehicle Routing Problem with Time Windows and Stochastic Travel Times
Hindawi出版公司,Discrete Dynamics in Nature and Society
大连理工大学,2016
关注点:时间窗口
三阶段方法:
-
转换阶段:时间窗终点往前挪一点,挪太多求解质量会下降,$lt_i’=lt_i-r\times \bar{Len}_i$,$0<r<1$,$Len_i$ 是其他点到 $i$ 的距离的平均
-
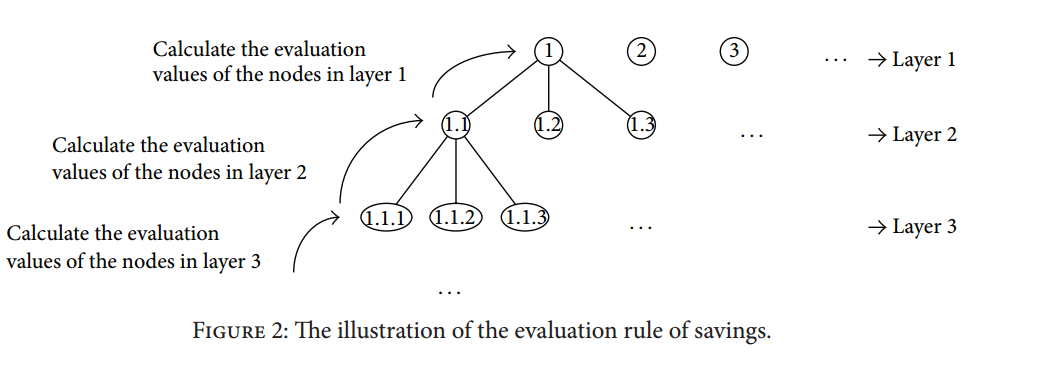
初始解:采用分层树状结构求 Saving 值,每次合并相当于合并两棵子树
-
-
\[EV_i=p\times SV_i+\frac{1-p}{ic}\times \sum_{j=1}^{ic}EV_j\]
$EV_i$ 是评估值,$SV_i$ 是 saving 值,$ic$ 是子节点数量。
- 后处理:采用迭代删除预留时间最小的顾客,并将顾客插入到其他路线或同一路线的其他位置,以获得总成本较小的解决方案。