TSP Ejection Chains

1997 Discrete Applied Mathematics

德国波恩大学经济与工商管理学院

前言

在上个世纪九十年代，有两个突出的弹射算法，一个是 LK 启发式，领域给是 eject chain。前者在 dismacs 上大放异彩，经过改良后成为现在最好的工业求解器之一。后者做不起来，但他理论上是完备的，仍有一些可做的空间。

摘要

基于一种特殊的参考结构，确定了旅行商问题的弹射链方法，用于生成与交变路径相关的结构。计算试验表明，该方法非常有效，在相同的时间框架内得到的解总体上优于改进的Lin-Kemighan方法。该方法目前在局部层面上有一个简单的禁忌搜索引导组件，也有潜力以更高级的方式与元启发式相结合，如遗传算法、模拟退火和禁忌搜索。

建模

基础概念

TSP 图 $G=(N,E)$，$N$ 是节点集合，边集 $E$ 是对称图 $c_{ij}=c{ji}$。目标是找到最小的 tour $T$ 使得 $c(T)=\sum(c_{ij}:(i,j)\text{ belongs to }T)$。

解用二元变量 $x_{ij}$ 表示 $T$ 是否经过 $(i,j)$。

r-exchanges 在 TSP 里表示为删除 r 条边再添加 r 条边，表现为在 $x$ 中有 r 个 0 变成 1 和 r 个 1 变成 0。为了确保仍然是一个 tour，TSP 中 $r\ge 2$。

交替路径和循环

很容易证明 TSP 的 r-exchange 可以分解成一个或者多个的交替循环的集合。

因此，这为开发基于交替路径概念的弹射链策略提供了自然的动机。然而，并不是所有的交替循环都能成功地将一个给定的循环转换成一个新的循环，因为任何子循环的集合也可以满足度约束（没法保证不出现自循环），并且交替循环也可以生成所有这样的子循环集合。

最小的 2-exchange 也叫做 2-opt。2-opt 建立在已有的解 $T$ 之上，$T$ 中的边叫做偶边，$E-T$ 中的边叫做奇边。一个交替循环必须至少包含 $E$ 中的两条边和 $E-T$ 中的两条边。

基础策略

初级弹射链方法旨在生成由交替循环和相关动态交替循环组成的动作。

配对步骤序列中的每一步，会引入和弹出一条边。

引入一个术语 1-exchange，对比 r-exchange，1-exchange 不会将一个 tour 转换成新的 tour。接下来将提出方案保证可以通过 1-exchange 操作后恢复可行解。

The stem-and-cycle reference structure

The stem-and-cycle reference structure 是一个生成子图，由一个与路径相连的循环组成，称为茎。表示茎与循环交点的节点称为根节点，用 $s$ 表示，与根相邻的两个循环节点称为子根。茎的另一端称为茎尖，用 $k$ 表示。

在下图（a）中，$s=1,k=3$。节点的标号表示访问的顺序表示从初始解开始需要修改结构的顺序。原本是 1-3-2 的，现在要添加 $(1,2)$ ，因此要删除 $(2,3)$。节点 1 的两个相邻点是子根。

茎是可以简并的，即 $s=k$，这样就变成了一个 tour。当茎是非简并的时候，有两种方法可以创建 tour。两种方法都是通过从尖端向其中一个子根 $s’$ 添加一天边 $(k,s’)$（当茎是简并的时候，添加和删除的是同一条边，不影响）。如图（b），一种情况就说这样，添加 3 和 1 的另一个未被访问的子根的边，并删除原来那条。另一种情况就是添加 $(3,2)$ 并删除 $(1,2)$，其实就是还原了。

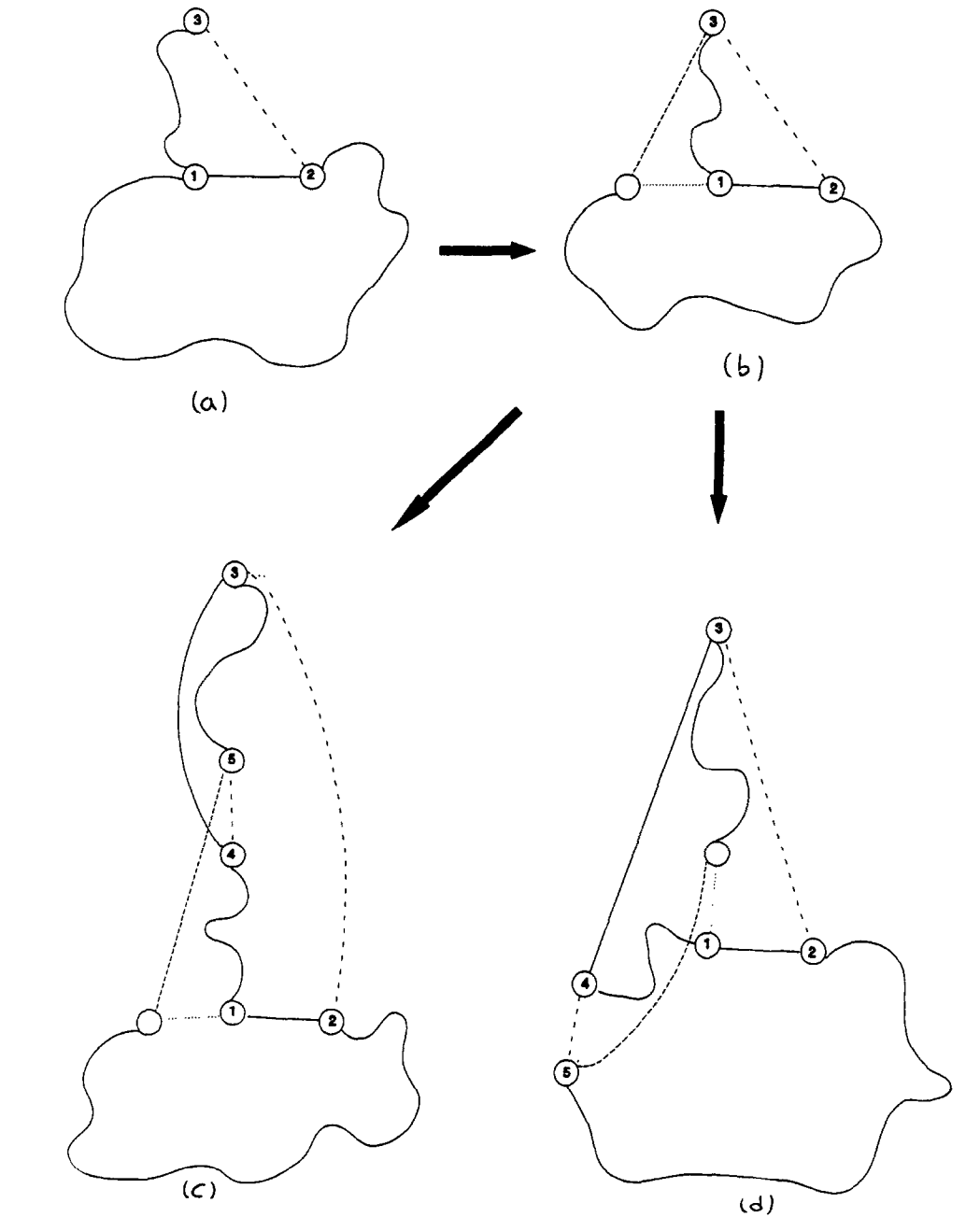
现在从图（b）出发，有两种情况，如图（c），可以添加 $(3,4)$ ，为了保持茎的结构，$(4,5)$ 就会被删除，然后 5 变成的新的尖端。如果 4 不在茎内，如图（d），添加 $(3,4)$ 后同样要删除 $(4,5)$。这样 2 就不是子根了。

强调 The stem-and-cycle reference structure 的两个特征：

总可以创建两个可行的 tour，即连接尖端和子根。
子根和根构成的三个节点中的两个节点，在一次移动后，子根可能会改变身份。

省流：

对于一个 TSP 环，添加一条边 $(i,j)$ 并删除 $(j,k)$，$k$ 是 $j$ 的邻居。

此时，TSP 环会变成一个根茎结构，$[k,\cdots,i]$ 是一条链，$[i,\cdots,j]$ 是一个环。
根茎结构可以通过，$k$ 向 $i$ 的两个邻居之一连边，并删除 $i$ 与其被连边的邻居的边，变成一个环。

Variable depth format

基于上述结构，首先提出该方法的限制版本，即Variable depth format。这种 format 的主要特点是将结构的每个部分都锁定在适当的位置，因此添加的任何元素（边缘）都不能删除，删除的任何元素都不能添加。

这种 format 要和禁忌搜索中的禁忌表结合。表中有两列，禁忌-删除和禁忌-添加表示历史动作，用于记录历史动作，接下来的动作不能通过之前的动作来获得。

直接看伪代码，文中的文字描述感觉有点乱，看不太懂。

解释一下：

while 的结束是直到禁忌表满了
每一步是找到一个最好的 pair $(i,j),(j,k)$，满足 $(i,j)$ 是不在 tour 的边且不在禁忌插入表中，$(j,k)$ 是在 tour 的边且不在禁忌删除表中，删除 $(j,k)$ 插入 $(i,j)$ 的收益最大。
弹射插入后更新完整的 tour 并记录最好的 tour。
repeat 的结束是没法更新更好的解了。

LK 算法算是上述算法的一个特例。

A localized tabu search format

上述 format 的结束条件是无法变得更好的，同事禁忌表也会限制一些动作。

简单来说就是给禁忌表中的元素添加时间，也就是过了很久禁忌表会遗忘掉一些长期记忆。

修改：放弃禁忌-删除表。

作者还提到了弹射链的其他方法，但他本身没有关注，只是举例。

实验结果不展开。