Learning Randomized Algorithms with Transformers

ICLR 2025

Google，ETH

摘要

随机化是一种强大的工具，它赋予算法非凡的属性。例如，随机算法在对抗设置中表现出色，通常超过具有较大边际的确定性算法的最坏情况性能。此外，他们的成功概率可以通过简单的策略，如重复和多数投票来扩大。在本文中，我们用随机化来增强深度神经网络，特别是Transformer模型。我们首次证明随机算法可以通过学习，以纯粹的数据和目标驱动的方式灌输到Transformer中。首先，我们分析了已知的对抗目标，其中随机算法比确定性算法提供了明显的优势。然后，我们展示了常用的优化技术，如梯度下降或进化策略，可以有效地学习变压器参数，利用提供给模型的随机性。为了说明随机化在增强神经网络中的广泛适用性，我们研究了三个概念性任务：联想回忆、图着色和探索网格世界的代理。除了通过学习随机化增强对无意识对手的鲁棒性外，我们的实验还揭示了由于神经网络计算和预测的固有随机性，性能得到了显著提高。

介绍

本文结合了随机化和深度学习的力量，特别是Transformer，并标明在对对抗目标进行优化时，发现了Transformer内部强大的随机化算法。这些Transformer算法在对抗无意识对手时具有更强的鲁棒性，并通过多数投票显著由于确定性策略。

一个简单例子，

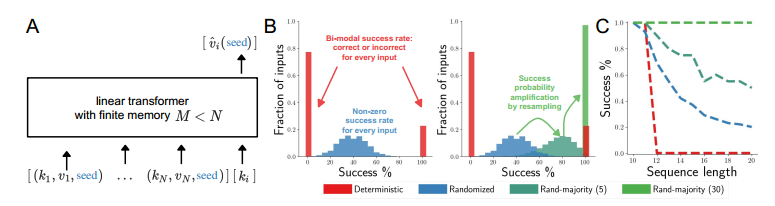
如A所示，一个计算机系统，存储容量为 $M$ 个向量，现在有 $N>M$ 个查询，希望给出一种存储策略，使得命中率尽量高。假设 Transformer 给出了一种确定策略是，始终保持序列中前 $M$ 个向量来存储，这样很容易构造出一种很差的询问序列，即不断查询编号 $k>M$ 的向量，这样每次都会失败。
现在考虑给 Transformer 新增一个额外的输入，即一个随机种子，并且基于这个种子，它均匀地随机选择要存储的数据。然后，每个查询将以 $1-\frac{M}{N}$ 的概率中断检索。因此，与确定性系统形成鲜明对比的是，不存在系统会特别糟糕的输入序列。特别是，任何对抗策略都不能使系统持续失败。换句话说，随机化可以改善最坏情况下的行为。
随机化可以通过重复提高训练过的Transformer的成功率。简单地在基于不同种子计算的 $M$ 个预测中获得多数投票，就可以提高性能，使其达到完美的成功率，远远超过确定性变压器——尽管网络容量和训练目标相同。

理论考量

一些符号化

将本文中的 Transformer 表示为 $A_\theta(x, r)$，其中输入为 $x \in \mathcal{X}$，随机性（或种子）为 $r\in\mathcal{R}$。定义两个随机变量 $X$（在 $\mathcal{X}$ 上）和 $R$（在 $\mathcal{R}$ 上）。对于任何参数 $\theta$，函数 $x \mapsto A_\theta(x, R)$ 是一个随机Transformer模型，也将其称为随机Transformer算法。
为Transformer模型提供随机种子编码（Random Seed Encoding, RSE），类似于Transformer模型中常见的位置编码。这种编码为Transformer提供随机性，通常是一个噪声向量（如随机比特），将它与输入标记拼接。
- 优化可以通过将第一层的权重设置为零来忽略 $R$，从而得到一个确定性Transformer。
当存在 $x \in \mathcal{X}$ 使得函数 $r \mapsto A_\theta(x, r)$ 不是常数时，称该Transformer是真正随机的。
对于任何固定的输入 $x \in \mathcal{X}$ 和 $r \in \mathcal{R}$，损失由 $L(x, A_\theta(x, r)) \geq 0$ 确定。
随机Transformer在输入 $x$ 上的性能是其期望损失，即 $E[L(A_\theta(x, R))]$。

（省流，只看标题就行了）

过多的模型容量不会强制使用随机性

随机化有益的第一个必要条件是模型容量不允许在不使用随机性的情况下达到最优性能，即忽略输入中的随机性。更准确地说，如果存在 $\theta$ 和 $r \in \mathcal{R}$，能够完美拟合数据，即对于所有 $x \in \mathcal{X}$，都有 $A_\theta(x, r) \in \arg\min_y L(x, y)$，那么随机性就没有被利用的动机。然而，优化算法是否会发现这样的 $\theta$ 并不能保证。常用的期望风险最小化（Expected Risk Minimization, ERM）或经验风险，在实践中，不应该导致随机化。

随机化在期望中并无益处

为了说明随机化在期望中并无益处，因此不太可能被优化利用以实现更低的损失，讨论 Yao 的 Minimax 原理。在随机化算法中，它提供了一个框架，用于理解随机化算法在对抗环境中表现如何。它可以表述如下，对于任意分布 $X$ 和 $R$：

\[\min_{r \in \mathcal{R}} E[L(A_\theta(X, r))] \leq L_E(\theta) := E[L(A_\theta(X, R))] \leq \max_{x \in \mathcal{X}} E[L(A_\theta(x, R))] \quad (1)\]

更直观地说，给定一个固定的数据分布，Yao 的 Minimax 原理表明：

第一个不等式：总存在一个确定性算法，在数据的期望性能上至少与随机化算法 $A(\cdot, R)$ 一样好。从随机化算法中提取一个特定种子，使其表现与随机化算法一样好的过程称为去随机化（derandomization）。然而，目前没有通用的高效方法来完成这一任务。
第二个不等式：任何随机化算法不可避免地会在某些输入上的表现比最佳确定性算法的平均性能更差。

乍一看，这一原理似乎否定了随机化算法相比确定性算法的优势。然而，上述原理适用于我们假设数据分布的设置，特别是当目标是经验风险最小化（ERM）时，优化固定数据集上的性能。因此，认识到深度学习中最常用的优化策略并不期望从随机化中受益。事实上，将通过实验证明，使用ERM训练的Transformer在变化的 $r$ 下不会产生随机预测，即ERM不会导致真正随机化的Transformer。

随机化在对抗环境中可能有益

如前所述，随机化在考虑数据的任意分布上的期望性能时并无优势。然而，当考虑对抗环境，特别是 Min-Max 设置时，情况会发生巨大变化。为了理解这些设置，首先定义一个无意识对手（oblivious adversary）：

定义 1（无意识对手）：无意识对手完全了解代理的算法，但无法控制随机性。

在上下文中，这样的对手知道算法 $A$ 和 $R$（种子的分布），但不知道 $R$ 的结果。然而，它可以选择输入的分布，因此可以将输入限制为 $\mathcal{X}$ 中最“困难”的实例。例如，在“石头-剪刀-布”游戏中，如果对手确定对手总是选择“石头”，那么它会一直出“纸”。与博弈论中的其他设置不同，这种对手并不是一个真正的对手，而是一个理论构造：代理实际上希望确保无论输入如何都能获得有利的结果。这种设置与 Min-Max 策略密切相关：面对无意识对手的代理旨在优化 Min-Max 损失，定义如下：

定义 2（Min-Max 损失）：Min-Max 目标是最小化以下损失：

\[L_A(\theta) := \max_{x \in \mathcal{X}} E[L(A_\theta(x, R))] \quad (2)\]

命题 1：随机化在最坏情况下有益假设 $X$ 是 $\mathbb{R}^d$ 的一个紧集，对于某个 $d$，且 $L$ 是连续的。进一步假设存在参数 $\theta^*$ 和一组随机种子 $(r_i)_{1 \leq i \leq N} \in \mathcal{R}^N$，使得对于每个 $i$：

\[\max_{x \in \mathcal{X}} L(A_{\theta^*}(x, r_i)) = \min_{\theta, r} \max_{x \in \mathcal{X}} L(A_\theta(x, r)), \quad \text{且} \quad \bigcap_i \arg\max_{x'} L(A_{\theta^*}(x', r_i)) = \emptyset \quad (3)\]

那么存在一个随机模型，其损失 $L_A$ 严格小于任何确定性模型。

需要注意的是，上述内容涵盖了更简单的论点，即如果模型能够完美拟合数据，则不会期望随机化。直观地说，该命题表明，只要存在多个可能的最优函数，这些函数可以在我们的模型类中实现，且不存在对所有函数都具有对抗性的输入 $x$，那么拥有这些函数的分布就比确定性地编码其中一种更有益。

通常可以通过优化模型分布的期望损失的 $q$-范数（对于 $q > 1$）来放松方程 2 中严格的对手，即：

\[\min_\theta L_q(\theta) = \min_\theta E[|E[L(A_\theta(X, R))|X]|^q]^{1/q} \quad (4)\]

这里，条件期望 $E[L(A_\theta(X, R))\mid X]$ 是对 $R$ 的平均损失。外层期望是对输入的期望。需要注意的是，当 $q = 1$ 时，$L_q = L_E$；当 $q = \infty$ 时，我们得到 $L_q = L_A$。

训练目标

基于前面关于随机化何时有益的描述，提出以下实际的训练目标：

\[\arg\min_\theta \hat{L}_q(\theta) = \arg\min_\theta \left( \frac{1}{n} \sum_{i=1}^{n} \left[ \frac{1}{m} \sum_{j=1}^{m} L(A_\theta(x_i, r_j)) \right]^q \right)^{1/q} \quad (5)\]

需要注意的是，这实际上是方程(4)的有偏近似。尽管在实践中，通过蒙特卡洛采样近似$q$-范数已知会缓慢收敛到期望值，在这里仍然使用它，并将更精细的采样方法的探讨留待未来工作。在训练目标中，与常见的数据期望损失的随机近似相比，引入了两个新的超参数，即$m$（考虑的随机种子数量）和$q$。将在实验结果部分分析这些超参数的作用，重点关注$q$的敏感性，因为它在ERM和对抗训练之间变化。

找到对抗性样本来计算方程(2)中的损失是困难的，特别是在计算梯度存在挑战的设置中，例如在语言任务中输入是离散的，或者在强化学习（RL）中。因此，通过优化$q < \infty$来近似最小最大对手的损失，可以得到一个实用的损失函数，而无需显式计算对抗样本。最后，需要注意的是，对抗性损失上界于期望损失，即$L_A(\theta) \geq L_E(\theta)$。然而，优化$L_A(\theta)$并不期望比直接优化$L_E(\theta)$获得更好的$L_E(\theta)$。

实验

略

讨论和相关工作

证明了通过优化选择随机性使Transformer模型具有与经典随机化算法相似的显著特性。具体来说，学习的随机Transformer算法在对抗性输入上显著优于确定性算法。
此外，在不同种子计算的预测中进行简单的多数投票，可以大大提高性能，远远超过确定性Transformer。
尽管如此，所提供的证据只是如何学习强大的随机神经网络算法的第一个概念步骤，尽管我们相信所提出的理论是通用的，适用于更实际的相关和大规模的设置。
此外，值得注意的是，方法的计算强度限制了我们方法当前形式的适用性和可扩展性。请注意，当与ERM训练模型进行比较时，超参数m将内存以及训练和推理时间（大致）按 $m$ 的因子进行缩放。