Neur2SP: Neural Two-Stage Stochastic Programming
NIPS2022
多伦多大学
开源: https://github.com/khalil-research/Neur2SP
摘要
随机规划是不确定性决策的一个有效的建模框架。在这项工作中,我们处理两阶段随机规划(2SP),最广泛使用的一类随机规划模型。精确求解2SP需要在计算上难以处理的期望值函数上进行优化。具有混合整数线性规划(MIP)或非线性规划(NLP)在第二阶段中,即使采用利用问题结构的专门算法,也会进一步增加棘手性。(第一阶段)解决方案-不利用问题结构-在这种情况下可能是至关重要的。我们开发了Neur2SP,一种新的方法,通过神经网络近似期望值函数,以获得代理模型,可以比传统的广泛制定方法更有效地解决。Neur2SP对问题结构没有任何假设,特别是关于第二阶段的问题,可以使用现成的MIP求解器来实现。我们对四个具有不同结构的基准2SP问题类进行了广泛的计算实验(包含MIP和NLP第二阶段问题)证明了效率(时间)和有效性Neur2SP在不到1.66秒的时间内,即使场景数量增加,Neur2SP也能在所有问题上找到高质量的解决方案,这是传统2SP解决方案技术难以拥有的理想属性。即,最通用的基线方法通常需要几分钟到几小时来找到质量相当的解决方案。
前序知识
两阶段随机规划 2SP
两阶段随机规划(2SP)可以一般性地表示为:
\[\min_{x} \{c^\top x + \mathbb{E}_\xi[Q(x, \xi)] : x \in X\}\]其中,
- $c \in \mathbb{R}^n$ 是第一阶段成本向量,
- $x \in \mathbb{R}^n$ 表示第一阶段决策,$X$ 是第一阶段的可行集,
- $\xi$ 是随机参数向量,其遵循概率分布 $P$,支撑集为 $\Xi$。
- 价值函数 $Q: X \times \Xi \rightarrow \mathbb{R}$ 表示在给定第一阶段决策 $x$ 的情况下,随机参数实现为 $\xi$ 时第二阶段(补偿)决策的最优成本。
在许多情况下,由于 $Q(x, \xi)$ 是通过求解数学规划得到的,因此计算期望值函数 $\mathbb{E}_\xi[Q(x, \xi)]$ 是不可行的。
为了提供一个更可行的公式化方法,通常使用扩展形式(Extensive Form, EF)。从概率分布 $P$ 中采样一组场景 $\xi_1, \dots, \xi_K$,扩展形式可以表示为:
\[\text{EF}(\xi_1, \dots, \xi_K) \equiv \min_{x} \left\{c^\top x + \sum_{k=1}^{K} p_k Q(x, \xi_k) : x \in X \right\}\]其中,$p_k$ 是场景 $\xi_k$ 实现的概率。如果 $Q(x, \xi) = \min_{y} {F(y, \xi) : y \in Y(x, \xi)}$,则 EF 可以表示为:
\[\min_{x,y} \left\{c^\top x + \sum_{k=1}^{K} p_k F(y_k, \xi_k) : x \in X, \ y_k \in Y(x, \xi_k) \ \forall k = 1, \dots, K \right\}\]该问题可以通过标准的确定性优化技术求解。然而,随着场景数量的增加,EF 中的变量和约束数量呈线性增长。此外,如果 $Q(\cdot, \cdot)$ 是一个混合整数规划(MIP)或非线性规划(NLP)的最优值,那么 EF 模型将显著更难以求解,尤其是与线性规划(LP)相比,这限制了其在小规模问题上的适用性。
Embedding Neural Networks into MIPs
(省流:一个带有ReLU激活函数的多层MLP,目标是用于预测价值函数Q的期望)
数学上,一个具有 $\ell$ 层的全连接神经网络可以表示为:
\[h_1 = \sigma(W_0 \alpha + b_0); \quad h_{m+1} = \sigma(W_m h_m + b_m), \quad m = 1, \dots, \ell - 1; \quad \beta = W_\ell h_\ell + b_\ell\]其中,$\alpha \in \mathbb{R}^m$ 是输入,$\beta \in \mathbb{R}$ 是预测值,$h_i \in \mathbb{R}^{d_i}$ 是第 $i$ 层的隐藏层,$W_i \in \mathbb{R}^{d_i \times d_{i+1}}$ 是从第 $i$ 层到第 $i+1$ 层的权重矩阵,$b_i \in \mathbb{R}^{d_i}$ 是第 $i$ 层的偏置,$\sigma$ 是非线性激活函数。在本文中,激活函数为 ReLU,即 $\sigma(a) = \max{0, a}$,其中 $a \in \mathbb{R}$。
Neur2SP 的核心是将训练好的神经网络嵌入到混合整数规划(MIP)中。在此,我们引用了 [Fischetti and Jo, 2018] 提出的公式。对于给定的隐藏层 $m$,第 $j$ 个隐藏单元 $h_{m,j}$ 可以表示为:
\[h_{m,j} = \text{ReLU}\left(\sum_{i=1}^{d_{m-1}} w_{m-1,ij} h_{m-1,i} + b_{m-1,j}\right)\]其中,$w_{m,ij}$ 是矩阵 $W_{m-1}$ 的第 $j$ 行第 $i$ 列的元素,$b_{m-1,j}$ 是 $b_{m-1}$ 的第 $j$ 个元素。为了在 MIP 中建模 ReLU 激活函数,我们引入变量 $\hat{h}_{m,j}$、$\check{h}_{m,j}$ 和 $\hat{h}_{m-1,i}$,其中 $i = 1, \dots, d_{m-1}$。ReLU 激活函数可以通过以下约束条件建模:
\[\begin{aligned} & \sum_{i=1}^{d_{m-1}} w_{m-1,ij} \hat{h}_{m-1,i} + b_{m-1,j} = \hat{h}_{m,j} - \check{h}_{m,j}, \\ & z_{m,j} = 1 \Rightarrow \hat{h}_{m,j} \leq 0, \\ & z_{m,j} = 0 \Rightarrow \check{h}_{m,j} \leq 0, \\ & \hat{h}_{m,j}, \check{h}_{m,j} \geq 0, \\ & z_{m,j} \in \{0, 1\}. \end{aligned}\]在上述公式中,逻辑约束(2b)和(2c)通过 MIP 求解器转换为大-M 约束。为了验证该公式化的正确性,观察到约束(2b)和(2c)与二进制变量 $z_{m,j}$ 的结合确保了 $\hat{h}_{m,j}$ 和 $\check{h}_{m,j}$ 中最多只有一个非零值。
此外,由于 $\hat{h}_{m,j}$ 和 $\check{h}_{m,j}$ 均为非负值,如果 $\sum_{i=1}^{d_{m-1}} w_{m-1,ij} \hat{h}_{m-1,i} + b_{m-1,j} > 0$,则 $\hat{h}_{m,j} > 0$ 且 $\check{h}_{m,j} = 0$;如果为负,则 $\hat{h}_{m,j} = 0$ 且 $\check{h}_{m,j} > 0$。因此,如果左侧为正,则 $\hat{h}_{m,j}$ 为正;如果为负,则 $\hat{h}_{m,j} = 0$,这正是 ReLU 函数的精确表示。
(上述式子分别是abcde,bc两条其实可以等价表示成等于)
Neur2SP架构
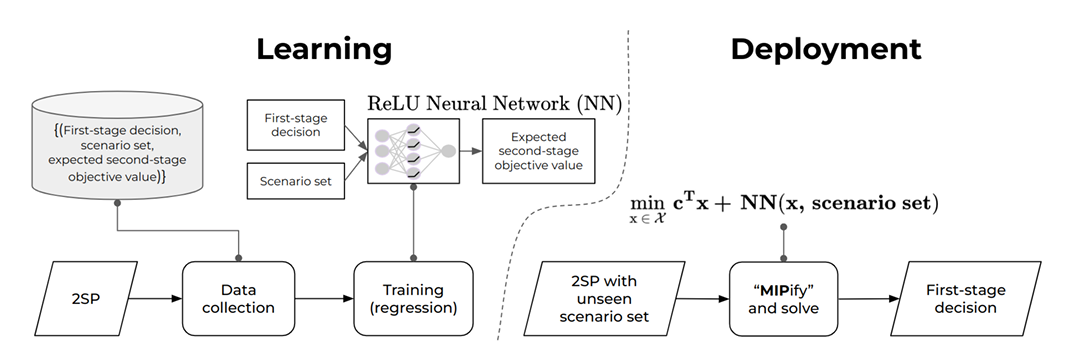
神经网络架构
(省流,两种框架,NN-E表示采样多种随机分布,NN的目标是使得目标函数在这些随机分布上的总目标函数最大;NN-P表示每次只在单个分布上训练,多次训练多个分布)
提出了两种不同的神经网络架构,用于预测第二阶段成本:NN-E 通过近似一组场景的第二阶段成本的期望值,而 NN-P 则近似单个场景的第二阶段成本值。
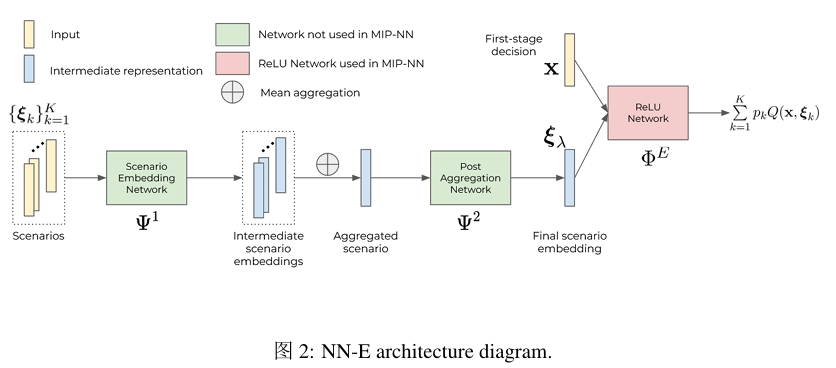
NN-E(上图)学习从 $(x, {\xi_k}_{k=1}^K) \rightarrow \sum_{k=1}^K p_k Q(x, \xi_k)$ 的映射。换句话说,该模型以第一阶段解 $x$ 和从不确定性集合 $\Xi$ 中采样得到的任意有限场景集作为输入,并输出对第二阶段目标值期望的预测。我们将每个场景独立地通过相同的神经网络 $\Psi_1$ 传递,然后对得到的 $K$ 个嵌入向量进行平均聚合。聚合后的嵌入向量通过另一个网络 $\Psi_2$ 得到场景集的最终嵌入表示 $\xi_\lambda$。这一嵌入表示与第一阶段决策拼接后,通过一个 ReLU 前馈网络 $\Phi_E$ 来预测第二阶段的期望值。因此,最终输出满足:
\[\Phi_E\left(x, \Psi_2\left(\bigoplus_{k=1}^K \Psi_1(p_k, \xi_k)\right)\right) \approx \sum_{k=1}^K p_k Q(x, \xi_k)\]注意,嵌入网络 $\Psi_1$ 和 $\Psi_2$ 可以是任意复杂的,因为只有潜在表示被嵌入到近似 MIP 中。此外,尽管 $\Psi_1$ 是使用 $K$ 个场景进行训练的,但一旦网络训练完成,它们可以用于任意(可能更大)的有限场景集。
NN-P 学习从 $(x, \xi) \rightarrow Q(x, \xi)$ 的映射,其中 $\xi$ 从不确定性集合 $\Xi$ 中采样。一旦学习到映射 $\Phi_P$,我们可以通过以下方式近似任意有限场景集的第二阶段目标值的期望:
\[\sum_{k=1}^K p_k Q(x, \xi_k) \approx \sum_{k=1}^K p_k \Phi_P(x, \xi_k)\]$\Phi_P$ 是一个前馈神经网络,其输入为 $x$ 和 $\xi$ 的拼接。
神经网络嵌入两阶段随机规划
现在描述上一节中提到的两种学习模型(NN-E 和 NN-P)的替代混合整数规划(MIP)。设 $\Lambda$ 表示神经网络的预测数量。对于 NN-E 情况,$\Lambda = 1$,因为我们只预测一组场景的期望第二阶段值。在 NN-P 情况下,$\Lambda = K$,因为我们为每个场景预测第二阶段值。在本节中,我们用 $[M]$ 表示集合 ${1, \dots, M}$,其中 $M \in \mathbb{Z}^+$。
设 $\hat{h}_{m,\lambda,j}$ 表示第 $m$ 层隐藏层中第 $j$ 个隐藏单元对应输出 $\lambda$ 的 ReLU 输出,对于所有 $m \in [\ell - 1]$,$j \in [d_m]$,和 $\lambda \in [\Lambda]$。假设 $\check{h}_{m,\lambda,j}$ 是用于建模第 $m$ 层隐藏层中第 $j$ 个隐藏单元对应场景 $k$ 的 ReLU 输出的松弛变量,对于所有 $m \in [\ell - 1]$,$j \in [d_m]$,和 $\lambda \in [\Lambda]$。设 $z_{m,\lambda,j}$ 是一个二进制变量,用于确保 $\hat{h}_{m,\lambda,j}$ 和 $\check{h}_{m,\lambda,j}$ 中最多只有一个非零值。该变量定义于所有 $m \in [\ell - 1]$,$j \in [d_m]$,和 $\lambda \in [\Lambda]$。假设 $\beta_\lambda$ 是神经网络的第 $\lambda$ 个预测值,对于所有 $\lambda \in [\Lambda]$。
通过上述变量,我们可以定义扩展形式(EF)的近似公式,如公式 (3) 所示。目标函数 (3a) 最小化第一阶段决策的成本与第二阶段值的近似成本之和。约束条件 (3b)-(3d) 将第一阶段解 $x$ 传播到每个场景的神经网络输出。约束条件 (3e)-(3h) 确保神经网络的预测被尊重。约束条件 (3i) 确保第一阶段解的可行性。
在这个近似中,我们引入了许多额外的变量和大-M 约束。具体来说,对于一个具有 $H$ 个隐藏单元的神经网络,我们引入了 $\Lambda \cdot H$ 个额外的二进制变量 $z_{m,\lambda,j}$。此外,我们引入了 $2 \cdot \Lambda \cdot H$ 个连续变量 $\hat{h}_{m,\lambda,j}$ 和 $\check{h}_{m,\lambda,j}$。最后,我们还需要额外的 $\Lambda$ 个变量用于网络的输出。尽管我们在这个近似中引入了大量的变量,但假设第二阶段问题是非线性的,我们推测得到的 MIP 将比扩展形式更容易求解。在本文的其余部分,我们将公式 (3) 中的替代 MIP 称为 MIP-NN。
\[\begin{aligned} & \min \quad c^\top x + \sum_{\lambda=1}^\Lambda p_\lambda \beta_\lambda && (3a) \\ & \text{s.t.} \quad \sum_{i=1}^{d_0} w_{0,ij} [x, \xi_\lambda]_i + b_{0,j} = \hat{h}_{1,\lambda,j} - \check{h}_{1,\lambda,j} && \forall j \in [d_1], \lambda \in [\Lambda], \quad (3b) \\ & \quad \quad \sum_{i=1}^{d_{m-1}} w_{m-1,ij} \hat{h}_{m-1,\lambda,i} + b_{m-1,j} = \hat{h}_{m,\lambda,j} - \check{h}_{m,\lambda,j} && \forall m \in [\ell - 1], j \in [d_m], \lambda \in [\Lambda], \quad (3c) \\ & \quad \quad \sum_{i=1}^{d_\ell} w_{\ell,ij} \hat{h}_{\ell,\lambda,i} + b_\ell \leq \beta_\lambda && \forall \lambda \in [\Lambda], \quad (3d) \\ & \quad \quad z_{m,\lambda,j} = 1 \Rightarrow \hat{h}_{m,\lambda,j} = 0 && \forall m \in [\ell - 1], j \in [d_m], \lambda \in [\Lambda], \quad (3e) \\ & \quad \quad z_{m,\lambda,j} = 0 \Rightarrow \check{h}_{m,\lambda,j} = 0 && \forall m \in [\ell - 1], j \in [d_m], \lambda \in [\Lambda], \quad (3f) \\ & \quad \quad z_{m,\lambda,j} \in \{0, 1\} && \forall m \in [\ell - 1], j \in [d_m], \lambda \in [\Lambda], \quad (3g) \\ & \quad \quad \hat{h}_{m,\lambda,j}, \check{h}_{m,\lambda,j} \geq 0 && \forall m \in [\ell - 1], j \in [d_m], \lambda \in [\Lambda], \quad (3h) \\ & \quad \quad x \in X && (3i) \end{aligned}\]数据生成
(省流:采样的分布多,状态大训练长收敛慢;采样的分布少,不准)
为了训练Neur2SP的监督式第二阶段价值近似模型,需要一个包含输入-输出对的多样化数据集。对于给定的两阶段随机规划(2SP)问题,我们采用迭代过程来生成这样的数据集。首先,生成一个随机的可行第一阶段决策。对于NN-E情况,我们从不确定性分布中随机采样一个具有随机基数$K’$的场景集。这里,$K’$的选择需要平衡在给定的第一阶段解下确定期望值所花费的时间和在给定时间预算内估计一组第一阶段决策的期望值之间的时间权衡。具体来说,如果$K’$较大,则平均而言,确定使用大量场景的期望值将花费更多时间;而对于较小的$K’$,由于期望值的估计速度更快,第一阶段决策空间将得到更多探索。对于给定的输入,即第一阶段决策和场景集,我们通过计算期望第二阶段价值$\sum_{k’=1}^{K’} p_{k’} Q_{k’}(\cdot, \xi_{k’})$来生成标签。
对于NN-P情况,在数据生成过程的每次迭代中,我们从不确定性分布中采样一个单一场景。对于给定的输入,即第一阶段决策和场景,我们通过计算其第二阶段价值$Q(\cdot, \cdot)$来生成标签。最后,将输入-输出对添加到数据集中。
这种数据生成过程可以完全并行化,以解决第二阶段问题。
NN-E与NN-P的权衡
(省流:NN-E更好)
NN-E和NN-P架构在学习任务和得到的替代优化问题方面存在权衡。
训练 在数据收集过程中,两种模型都需要在固定第一阶段解的情况下求解第二阶段问题以获得标签。对于NN-P,每个样本只需要解决一个优化问题,而NN-E的每个样本最多需要解决$K’$个第二阶段问题。由于这一过程是离线的且高度可并行化,因此这种权衡很容易缓解。在训练方面,NN-E操作于一个场景子集,这使得输入空间呈指数级增长。尽管输入空间很大,但我们的实验表明,NN-E模型在训练中收敛得很好,在许多情况下,嵌入的模型比NN-P模型表现更好。
替代优化问题 由于最终目标是将训练好的模型嵌入到MIP中,因此这方面的权衡变得尤为重要。具体来说,对于$K$个场景,NN-P模型将比NN-E模型多出$K$倍的二进制变量和连续变量。对于具有大量场景的问题,这使得NN-E模型更具吸引力,更小且可能更快求解。此外,它还允许使用更大的网络,因为只需嵌入一个网络副本。
实验
实验配置:
- IntelXeonCPUE5-2683和Nvidia Tesla P100 GPU,并具有 64GB 的 RAM (用于训练)
- Gurobi 9.1.2 作为 MIP 求解器
问题集:

- 容量设施选址 CFLP
- 投资问题 INVP
- 随机服务器选址问题 SSLP
- 池问题 PP
baseline:
- EF,3小时,唯一可应用于整数和非线性第二阶段问 题的通用方法
- 线性回归器取代神经网络,很糟糕
模型和数据集选择:
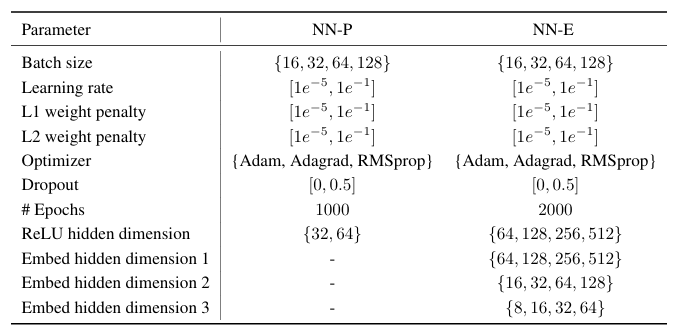
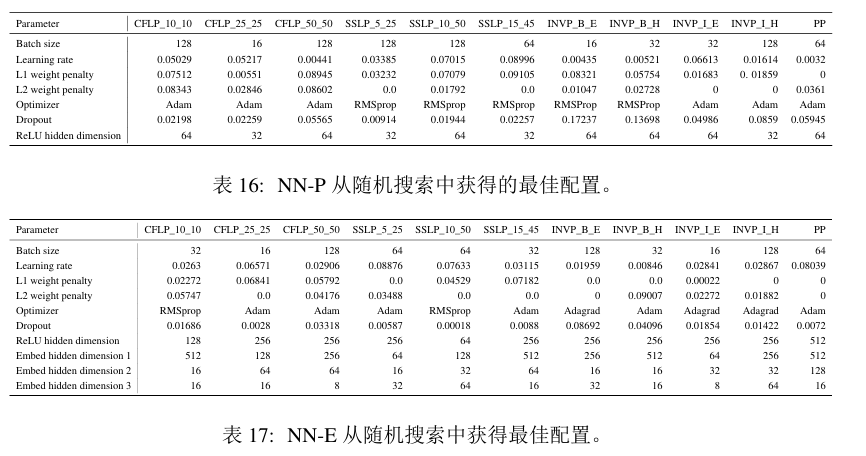
最佳超参数:
验证集:5000,训练集:100 500 1000 5000 10000 20000
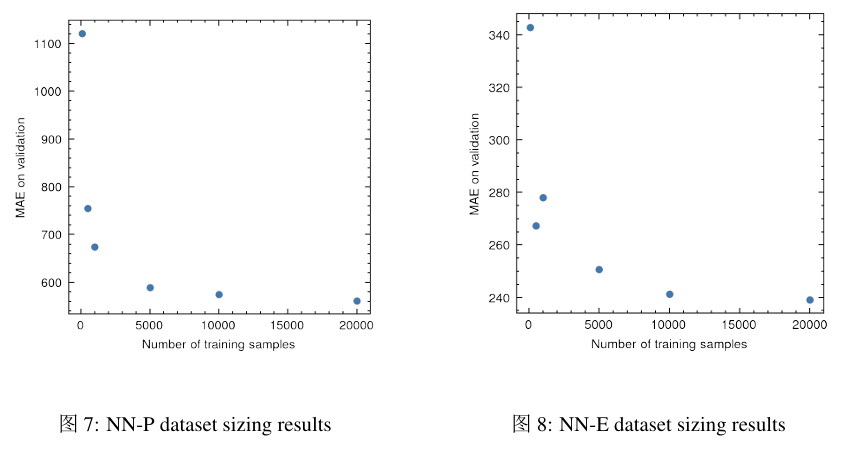
实验标明 5000 最好。验证均方误差(MSE)。
数据生成和模型训练时间
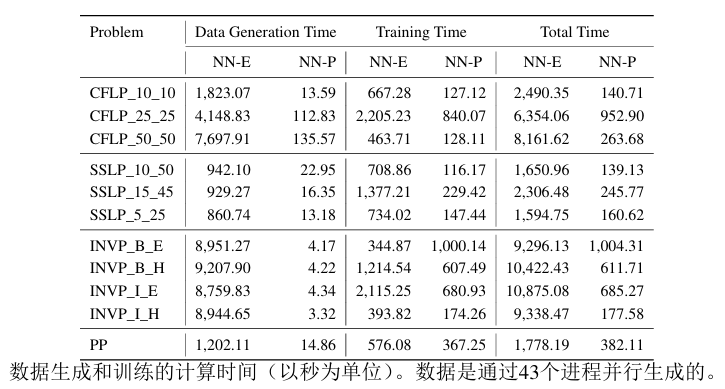
NN-E:100个分布。
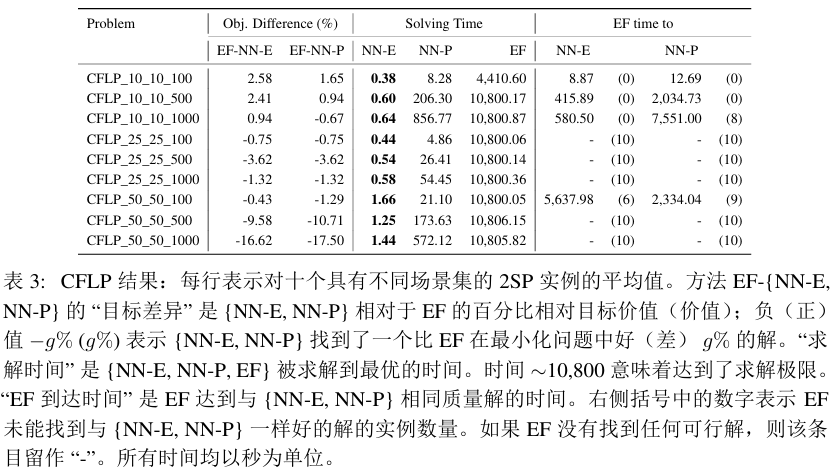
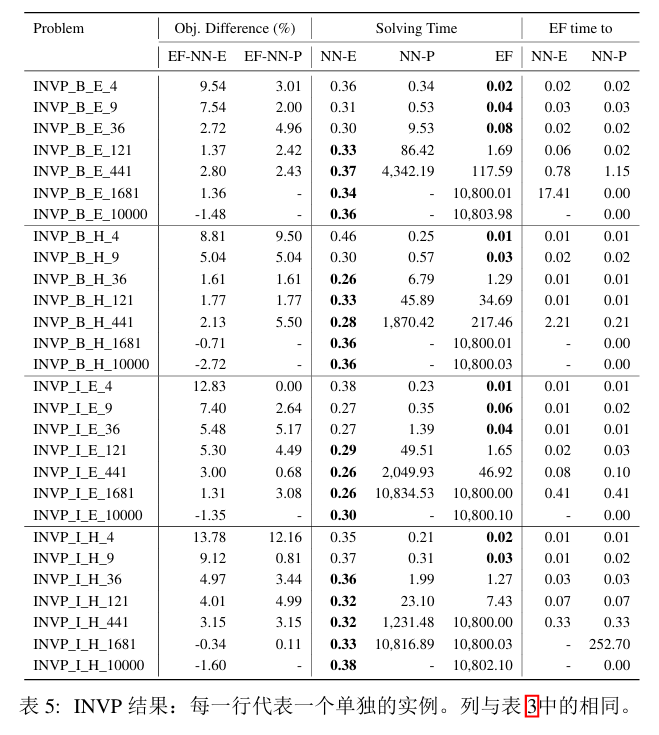
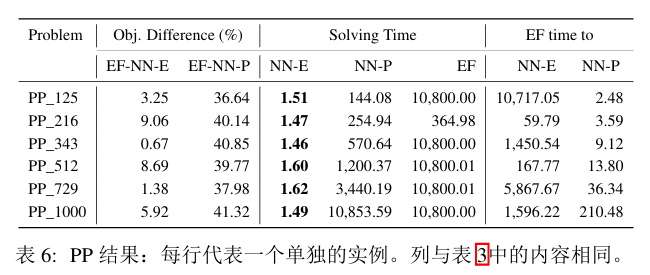
实验结果
(省流:NN-E求解效率很高,而且质量也不错。NN-P的优势是需要数据少且训练时间短。)
CFLP_设施数量_顾客数_场景数