A Machine Learning Approach to Solve the E-commerce Box-Sizing Problem

来自：印度

发表：Production and Operations Management

投稿时间：2023.11，接受时间：2024.8

研究背景与问题

如何为电子商务平台上的大量商品（SKU）设计一组最优的包装盒尺寸，以最大化空间利用率并降低包装和运输成本。

方法

论文提出了一种基于机器学习的三阶段优化框架，结合了无监督学习、强化学习和树搜索技术，以解决包装盒尺寸优化问题。具体方法如下：

第一阶段：生成初始解

将每个SKU视为三维空间中的一个数据点，使用K-means聚类算法将SKU划分为K个簇。
每个簇对应一个包装盒，簇中SKU的最大尺寸决定了该盒的尺寸。
这种方法快速生成初始解，为后续优化提供起点。

关于包装盒的旋转：

假设一个SKU的尺寸是 $l\times b\times h$，其中 $l\ge b\ge h$。
在包装盒中，这个SKU可以以三种不同的方向放置：
1. $l$ 作为长度方向，$b$ 作为宽度方向，$h$ 作为高度方向。
2. $l$ 作为长度方向，$h$ 作为宽度方向，$b$ 作为高度方向。
3. $b$ 作为长度方向，$l$ 作为宽度方向，$h$ 作为高度方向。

第二阶段：学习改进启发式规则

将包装盒尺寸优化问题转化为一个序列决策任务，称为“包装盒尺寸游戏”。这个序列决策任务可以通过马尔科夫决策过程建模。
- 状态：每个包装盒由其长度、宽度和高度定义，因此状态可以表示为一个矩阵，其中每一行对应一个包装盒的三个维度。如果有 $ K $ 个包装盒，状态可以表示为一个 $ K \times 3 $ 的矩阵。
- 动作：增加或减少某个维度的大小，或者，保持当前状态不变并结束游戏。具体来说，对于 $ K $ 个包装盒，每个包装盒有3个维度，因此总共有 $ 6K $ 种调整动作（每个维度可以增加或减少）。此外，还有一个“结束游戏”的动作，因此总共有 $ 6K + 1 $ 种可能的动作。
- 奖励：奖励函数的设计目标是减少包装盒的空隙率。
  \[r(s_t, a_t, s_{t+1}) = \begin{cases} \text{PF}(s_t) - \text{PF}(s_{t+1}), & \text{如果 } s_{t+1} \text{ 是可行的且状态变好} \\ -1, & \text{如果 } s_{t+1} \text{ 不可行或状态变差} \\ 0, & \text{如果智能体选择结束游戏} \end{cases}\]
  其中，$\text{PF}(s)$ 表示状态 $ s $ 的包装因子，用于衡量包装盒的空隙率。
  \[\text{PF} = \frac{\sum_{i \in D} \sum_{j \in P} d_i \cdot L_j \cdot B_j \cdot H_j \cdot x_{ij}}{\sum_{i \in D} d_i \cdot l_i \cdot b_i \cdot h_i}\]
  其中，
  - $ D $ 是所有商品（SKU）的集合，每个商品 $ i $ 有其长度 $ l_i $、宽度 $ b_i $、高度 $ h_i $ 和需求量 $ d_i $。
  - $ P $ 是所有包装盒的集合，每个包装盒 $ j $ 有其长度 $ L_j $、宽度 $ B_j $ 和高度 $ H_j $。
  - $ x_{ij} $ 是一个二进制决策变量，表示商品 $ i $ 是否被分配到包装盒 $ j $ 中（$ x_{ij} = 1 $ 表示分配，$ x_{ij} = 0 $ 表示未分配）。
使用神经网络代理学习改进初始解的策略。神经网络通过强化学习（特别是近端策略优化，PPO）训练，学习如何调整盒子尺寸以减少空隙。
- 网络（MLP）：输入状态，通过2到3层带有ReLU的全连接层，映射到动作空间进过Softmax作为输出。

第三阶段：树搜索优化

将第二阶段学习到的策略与树搜索算法结合，进一步优化初始解。

初始状态：从第二阶段生成的优化后的状态开始。
动作选择和模拟
- 动作选择：通过网络输出的动作概率向量来评估动作的优劣
- 动作模拟：通过不断调用网络探索，直到预设的深度 $\tau$
评估动作的长期效果：引入了一个加权包装因子，其实就是其实就是有折扣因子的累计回报
- $\text{WPF} = \text{PF}_x + \beta \cdot \text{PF}_1 + \beta^2 \cdot \text{PF}_2 + \dots + \beta^{\tau-1} \cdot \text{PF}_\tau$
选择最优动作：根据加权包装因子值最小的动作作为当前步骤的最优动作。
重复上述步骤，直到达到预设的搜索深度或找到满意的状态。

实验与结果

论文使用了来自一家大型电子商务平台的真实数据集进行实验，数据集包含153,625个SKU的尺寸和需求信息。

box assortment：包装箱种类

神经网络的表现

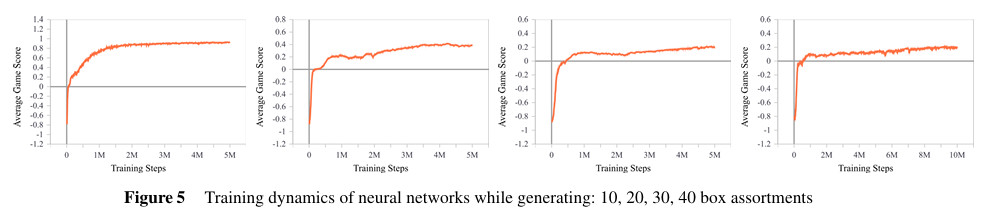
在训练初期，网络可能会使解决方案恶化，环境会因高负分而终止游戏。然而，随着训练的进行，网络学会了在改进和恶化之间做出选择，并逐渐减少负分的出现。在训练的后期阶段，神经网络学会了只采取改进措施，并在不进入不可行状态的情况下持续获得正向奖励。

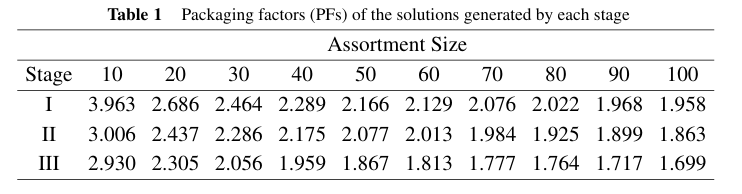
每个阶段的增量价值

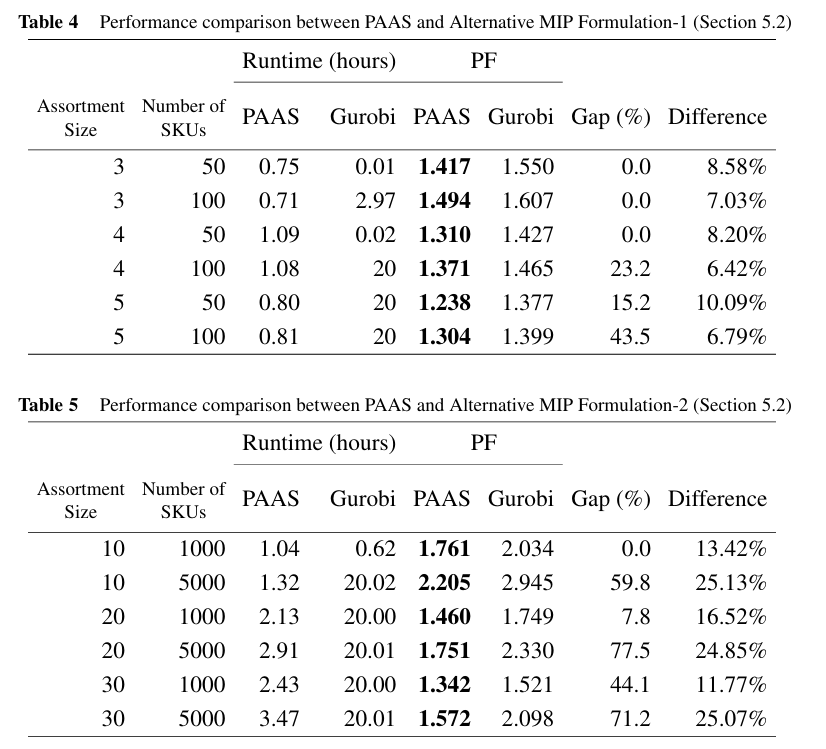
与另外两种MIP建模方式比较

表4是1范数建模，表5是无穷范数建模。

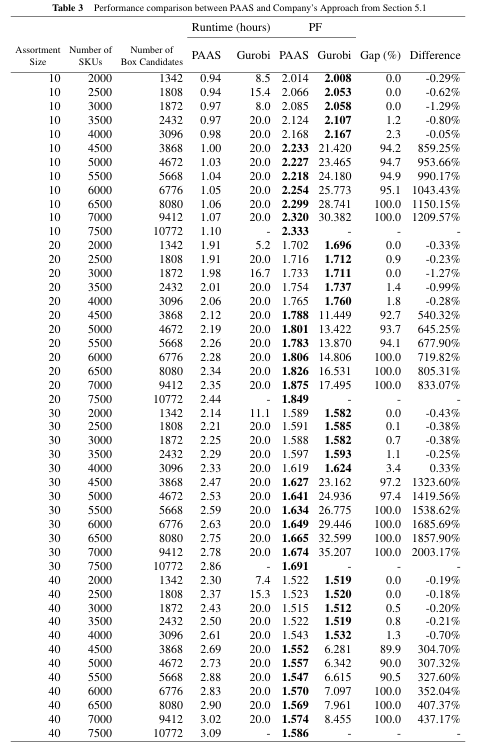
机器学习方法和MIP方法的比较

PAAS：文章设计的机器学习方法的名称。

阶段一方法的选择

聚类方法需要满足：

必须分配所有的SKU
必须生成固定数量的簇

因此，许多流行的聚类方法（如亲和力传播、DBSCAN、均值漂移及其变体）不能使用，因为它们不分配所有数据点或不生成固定数量的簇。这使得我们只剩下几种流行的替代方法，例如层次聚类（Agglomerative Clustering）和谱聚类（Spectral Clustering）。

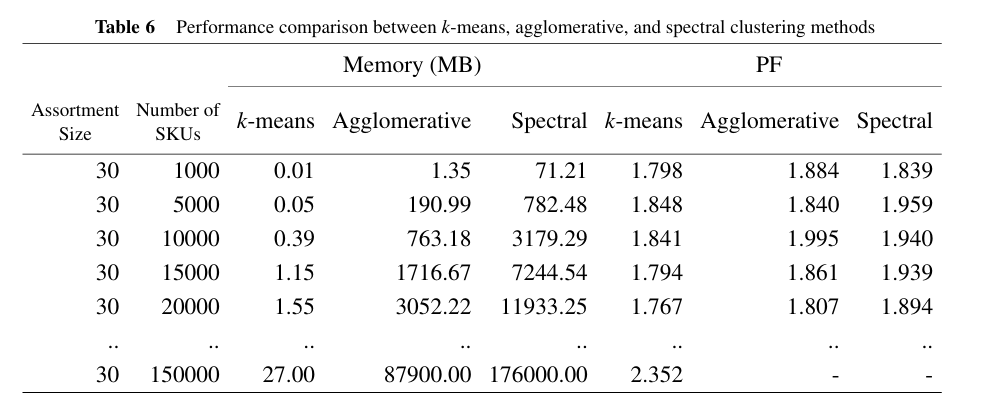
k-means方法得到的PF不差于另外两种，且层次聚类和谱聚类方法的内存消耗随着SKU数量的增加而呈二次方增长。

（OS：没有不是聚类的方法吗）

研究贡献与实践意义

性能提升：通过三阶段优化框架，最终的包装盒尺寸方案显著优于初始解，平均包装因子（PF）降低了约15%。
计算效率：与传统的数学规划方法相比，该机器学习方法能够在短时间内处理大规模问题，而传统方法在处理数千个SKU时就显得力不从心。
环境影响：优化后的包装盒方案每年可为公司节省约710万美元的成本，同时减少2080吨纸张消耗和1960吨温室气体排放。

研究贡献

提出了一种创新的机器学习方法，解决了电子商务包装盒尺寸优化这一实际问题。
展示了无监督学习、强化学习和树搜索技术在优化问题中的协同应用。
为机器学习在运营管理中的应用提供了新的视角。

实践意义

该方法已被一家大型电子商务公司采用，并在其28个物流中心推广，显著降低了包装成本和运输成本。
该框架具有普适性，可应用于其他电子商务平台或物流场景。