Learning What to Defer for Maximum Independent Sets

ICML2020

KAIST

摘要

设计高效的组合优化算法在各个科学领域中普遍存在。近年来，深度强化学习（DRL）框架作为一种新方法受到了相当多的关注：它们可以在依赖较少目标问题的专业知识的情况下自动化求解器的设计。然而，现有的DRL求解器通过与解中元素数量成比例的阶段数来确定解，这严重限制了它们在大规模图上的适用性。在本文中，我们提出了一种新的DRL方案，称为“学习延迟决策”（LwD），其中代理通过学习在每个阶段分配解的逐元素决策，自适应地收缩或拉伸阶段数量。我们将所提出的框架应用于最大独立集（MIS）问题，并展示了其与当前最先进的DRL方案相比的显著改进。我们还表明，LwD可以在有限的时间预算内，针对具有数百万顶点的大规模图，超越传统的MIS求解器。

引入

贡献

提出了一个新的DRL框架，Learning what to defer（LwD），用于解决大规模组合优化问题，该框架是为局部可分解问题设计的，其中可行性约束和目标可以通过局部连接的变量（在图中）分解。
- 代表性例子：可满足性、最大割、图染色。本文关注最大独立集。
创新点：迭代地确认每个未确定的节点，（a）确定顶点在解中的成员资格；（b）推迟。
- 灵感来自survey propagation，可以被解释为优先考虑“更容易”的决定
基于这样的加速，LwD可以通过在有限的时间预算内生成大量候选解来解决优化问题，然后报告其中的最佳解。对于这种情况，算法可以生成不同的候选。为此，我们在训练期间额外给我们的代理一个新的多样化奖金，这明确地鼓励代理生成各种各样的解决方案。具体地说，我们创造了一个“耦合”的MDP生成两个解决方案，为给定的MIS问题，并奖励代理之间的解决方案的大偏差。由此产生的奖励有效地提高在评估中的表现。

方法

给定一个图 $ G = (V, E) $ ，其中包含顶点集 $ V $ 和边集 $ E $ ，独立集是指 $ V $ 的一个子集 $ I \subseteq V $ ，其中任意两个顶点都不相邻。MIS问题的解可以表示为一个二进制向量 $ x = [x_i : i \in V] \in {0, 1}^V $ ，其目标是最大化独立集的大小 $ \sum_{i \in V} x_i $ ，其中每个元素 $ x_i $ 表示顶点 $ i $ 是否属于独立集 $ I $ ，即当且仅当 $ i \in I $ 时 $ x_i = 1 $ 。

最初，算法对输出没有假设，即对于所有 $ i \in V $ ， $ x_i = 0 $ 和 $ x_i = 1 $ 都是可能的。在每次迭代中，代理对每个未确定的顶点 $ i $ 执行以下操作之一：

（a）确定其是否属于独立集，即设置 $ x_i = 0 $ 或 $ x_i = 1 $ ；

（b）将决策推迟到后续迭代中进行。

代理重复此操作，直到确定所有顶点在独立集中的成员身份。可以将这种策略解释为在每次迭代中逐步缩小候选解的范围。直观上，延迟决策的策略是优先选择“较容易”的顶点的值。在每次决策后，“难”顶点变得更简单，因为其周围“容易”顶点的决策已更好地确定。

LwD适用于除MIS问题之外的组合优化问题，例如通过考虑非二进制向量 $ x $ 的决策。特别是，LwD框架适用于局部可分解的组合问题，即可行性约束可以通过局部连接变量进行分解的问题。像可满足性（SAT）、最大割（MAXCUT）和图着色等流行问题也属于这一类别。对于这些问题，一次对多个“局部”变量进行决策可能不会违反可行性，而这正是LwD高效实现所需的关键。

延迟马尔可夫决策过程

状态：MDP的每个状态表示为一个顶点状态向量 $ s = [s_i : i \in V] \in {0, 1, *}^V $ ，其中顶点 $ i \in V $ 被确定为排除在独立集之外或包含在独立集中时，分别有 $ s_i = 0 $ 或 $ s_i = 1 $ 。否则， $ s_i = * $ 表示该决策被推迟，预计将在后续迭代中做出。MDP初始化时所有顶点状态均为推迟状态，即对所有 $ i \in V $ ，有 $ s_i = * $ ，并在以下两种情况之一发生时终止：（a）没有剩余的推迟顶点状态；（b）达到时间限制。（省流：当前MIS每个节点的状态，分别表示确定要、确定不要、推迟）

动作：动作对应于顶点的下一个状态的新赋值。由于已确定的顶点状态（包含或排除）是不可变的，因此赋值仅定义在推迟决策的顶点上。它表示为一个向量 $ a^\ast = [a_i : i \in V^\ast] \in {0, 1, *}^{V^\ast} $ ，其中 $ V^\ast $ 表示当前推迟决策的顶点集合，即 $ V^\ast = {i : i \in V, x_i = *} $ 。（省流：对推迟的节点进行状态选择）

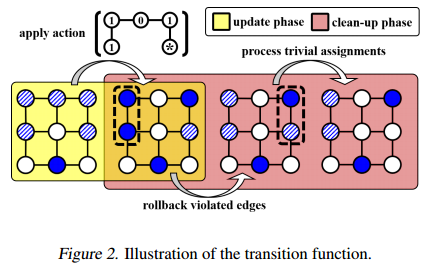
转移：给定两个连续状态 $ s $ 和 $ s’ $ 以及相应的赋值 $ a^\ast $ ，转移 $ P_{a^\ast}(s, s’) $ 包括两个确定性阶段：更新阶段和清理阶段。更新阶段考虑策略为对应顶点 $ V^\ast $ 生成的赋值 $ a^\ast $ ，以得到一个中间顶点状态 $ \tilde{s} $ ，即当 $ i \in V^\ast $ 时， $ \tilde{s}_i = a_i $ ，否则 $ \tilde{s}_i = s_i $ 。清理阶段将中间顶点状态向量 $ \tilde{s} $ 修改为有效的顶点状态向量 $ s’ $ ，其中包含的顶点仅与排除的顶点相邻。清理阶段会修改中间顶点状态向量 $ \tilde{s} $ ，以得到有效的顶点状态向量 $ s’ $ ，其中包含的顶点仅与排除的顶点相邻。具体来说，当存在一对相邻的包含顶点时，它们会被重新映射回推迟状态。接下来，MDP会排除任何与包含顶点相邻的推迟状态顶点。见图2，更详细地展示了两个状态之间的转换。

当MDP做出所有决策时，即在终止时，可以（可选地）通过应用 2-opt 局部搜索算法来改进确定的解，该算法通过贪婪地移除一个顶点并添加两个顶点来增加独立集的大小，直到无法再进行修改。

（省流：如果动作中包含相邻的确定要的节点，这时候违反了MIS的约束，所以重新变回延迟。最后可以做一个 2-opt 改进。）

奖励：最后，我们定义基数奖励 $ R(s, s’) $ 为包含顶点数量的增加。具体来说，定义为 $ R(s, s’) = \sum_{i \in V^\ast \setminus V’^\ast} s’_i $ ，其中 $ V^\ast $ 和 $ V’^\ast $ 分别是关于状态 $ s $ 和 $ s’ $ 的推迟状态顶点集合。通过这种方式，MDP的总奖励对应于我们的算法返回的独立集的基数。

解决方案多样化奖励

引入了一个额外的多样化奖励，以鼓励代理生成多样化的解决方案。这种正则化是出于评估方法的动机，该方法通过采样多个候选解决方案并报告其中最佳的一个作为最终输出。在这种情况下，生成具有高最大得分的多样化解决方案是有益的，而不是生成得分相似的解决方案。为此，将两个相同的图 $ G $ 上的马尔可夫决策过程的副本“耦合”成一个新的MDP。然后，新MDP与一对不同的顶点状态向量 $ (s, \bar{s}) $ 相关联，这些向量来自耦合的MDP。此外，相应的代理独立工作，生成一对解决方案 $ (x, \bar{x}) $ 。然后，我们直接根据 $ L1 $ 范数奖励耦合解决方案之间的偏差，即 $ \mid x - \bar{x}\mid_1 $ 。具体来说，偏差被分解为每个迭代的奖励，定义为：

\[R_{\text{div}}(s, s', \bar{s}, \bar{s}') = \sum_{i \in \Delta V} |s'_i - \bar{s}'_i|\]

其中 $ \Delta V = (V^\ast \setminus V’^\ast) \cup (\bar{V}^\ast \setminus \bar{V}’^\ast) $ ， $ (s’, \bar{s}’) $ 表示耦合MDP中下一对顶点状态。这里 $ \Delta V $ 表示每个MDP中最近更新的顶点。实际上，这种奖励 $ R_{\text{div}} $ 可以与最大熵正则化一起使用，以实现最佳性能。见图3，展示了带有提议奖励的耦合MDP的示例。

我们注意到，策略的熵正则化在鼓励探索方面与我们的多样化奖励有类似的作用。然而，熵正则化试图生成同一MDP的不同轨迹，这并不一定能导致最终的多样化解决方案，因为许多轨迹可能会导致相同的解决方案。相反，我们通过一个新的奖励项直接最大化解决方案之间的多样性。

我们还观察到，这种多样化奖励机制在训练过程中能够显著提高算法的性能，尤其是在面对大规模图和复杂结构时，能够帮助代理更好地探索解空间，避免陷入局部最优解。

（省流，一次生成两个解，用两个解的距离作为奖励）

PPO训练

算法使用图神经网络架构（GraphSAGE）构建的策略网络 $ \pi(a\mid s) $ 和价值网络 $ V(s) $ 。每个网络由多层组成，第 $ n $ 层的权重为 $ W^{(n)}_1 $ 和 $ W^{(n)}_2 $ ，对输入 $ H $ 进行以下变换：

\[h^{(n)}(H) = \text{ReLU}\left(HW^{(n)}_1 + D^{-\frac{1}{2}} B D^{-\frac{1}{2}} HW^{(n)}_2\right)\]

其中， $ B $ 和 $ D $ 分别是图 $ G $ 的邻接矩阵和度矩阵。在最后一层，策略网络和价值网络分别应用Softmax函数和图读出函数（使用求和池化），以生成动作和价值估计。使用顶点的度和MDP的当前迭代索引作为神经网络的输入特征。MDP的迭代索引被归一化到最大迭代次数。仅考虑由推迟决策的顶点 $ V^\ast $ 诱导的子图作为网络的输入，因为已确定的部分图不再影响MDP的未来奖励。

为了训练代理，使用近端策略优化（PPO）。具体来说，我们训练网络以最大化以下目标函数：

\[L := \mathbb{E}_t\left[\min\left(\frac{A(t)}{\pi_{\text{old}}(a^{(t)}_i \mid s^{(t)})}, \frac{\pi(a^{(t)}_i \mid s^{(t)})}{\pi_{\text{old}}(a^{(t)}_i \mid s^{(t)})}\right)\right]\]

其中：

$ s^{(t)} $ 、 $ a^{(t)} $ 、 $ R^{(t)} $ 和 $ R^{(t)}_{\text{div}} $ 分别表示第 $ t $ 个顶点状态向量、动作向量、基数奖励和多样化奖励。
$ \pi_{\text{old}} $ 是上一次迭代更新的策略网络。
$ T $ 是MDP的最大步数。
$ \alpha \geq 0 $ 是一个可调的超参数。
$ \text{clip}(r, r_{\min}, r_{\max}) $ 是一个截断函数，将动作概率比 $ r $ 投影到区间 $ [r_{\min}, r_{\max}] $ 内，以保守地更新代理。注意，这里的截断是针对每个顶点进行的，与原始框架中仅进行一次截断不同。

实验

实验设备：

单个GPU（NVIDIA RTX 2080 Ti）和单个CPU（Intel Xeon E5-2630 v4）

baseline：

强化学习：S2V-DQN
监督学习：TGS
求解器：CPLEX、KaMIS
AM不用，因为这是专门解TSP类的

数据集：

合成数据集：ER、BA、HK、WS
真实世界数据集：SATLIB、PPI、REDDIT-M-5K、REDDIT-M-12K、REDDIT-B、as-Caida

评估

中等规模图（最大30000节点）

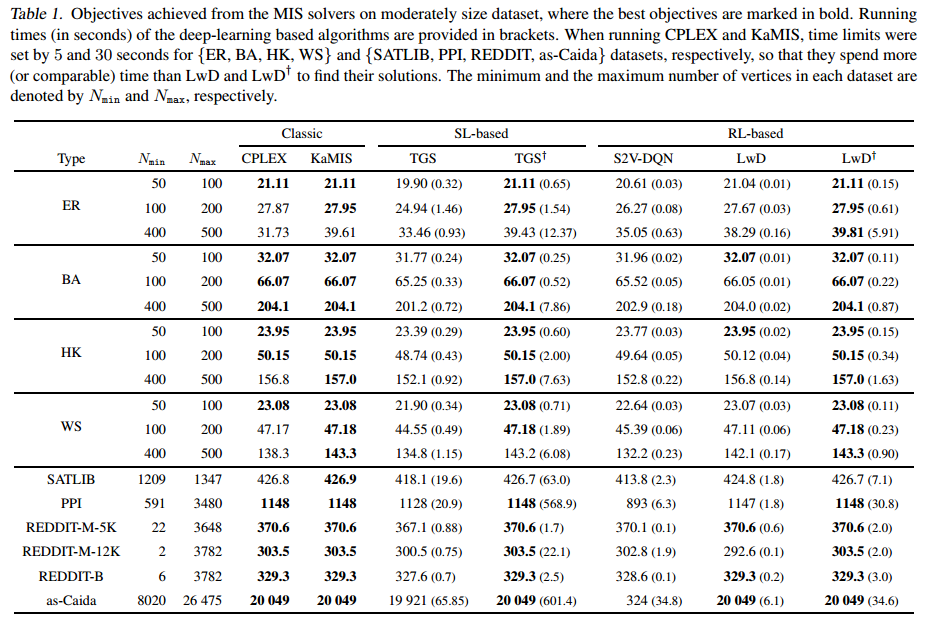
除了SATLIB，表现均为最好。甚至在某些数据集上比求解器还要好。但总体来说，规模越大，gap越大。

百万规模图

CPLEX和KaMIS的时间限制为1000秒。括号内是运行时间。

目标函数和求解时间的权衡

合理的求解时间内，性能更好。

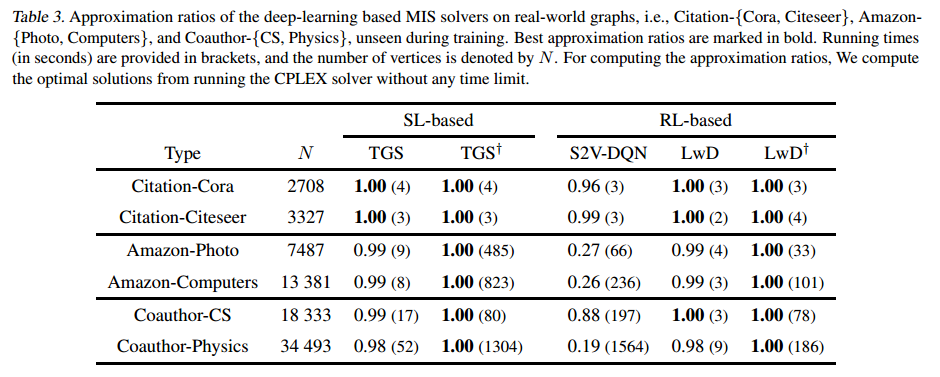
泛化能力

泛化到不同分布。括号内是运行时间。

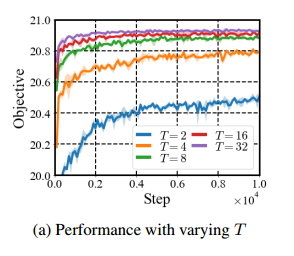
消融实验

defer的有效性：T是迭代轮数，轮数越多越好
解的多样性
- 没有探索奖励，baseline
- 传统的熵奖励
- 多样化奖励
- 熵+多样化奖励
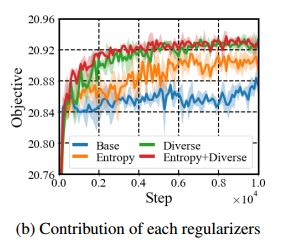
- 熵+多样性更好，熵其实用处不大
- 进一步算了一个系数，这个系数是下一轮不等于上一轮解的比例

其他问题实验

CPLEX限制5秒。这是二次整数规划问题。