PolyNet: Learning Diverse Solution Strategies for Neural Combinatorial Optimization
ICLR2025
Bielefeld University,Germany
摘要
基于强化学习的方法在构建组合优化问题的解决方案方面,正迅速接近人工设计算法的性能水平。为了进一步缩小这一差距,基于学习的方法必须在搜索过程中高效地探索解空间。近期的方法通过强制生成多样化的解决方案来人为增加探索性,但这些规则可能会损害解决方案的质量,且对于更复杂的问题而言,设计此类规则十分困难。在本文中,我们提出了一种名为 PolyNet 的方法,通过学习互补的解决方案策略来提升解空间的探索效率。与其他工作不同,PolyNet 仅使用单一解码器和一种不依赖于人为规则强制生成多样化解决方案的训练方案。我们在四个组合优化问题上对 PolyNet 进行了评估,观察到其隐式的多样化机制使得 PolyNet 能够找到比那些依赖强制多样性生成方法更优的解决方案。
引入
现有方法的局限
- 难以充分探索解空间
- POMO通过构造期间强制不同的第一个操作来改进探索,但这种操作仅在TSP等对称问题中有效
- 还有一种操作是,一种具有多个解码器的模型,同时最大化解码器输出概率之间的KL散度以促进生成不同的解
- Poppy也是多解码器,但他不依赖KL散度,他的目标函数设计为只用最优的答案来更新所有解码器
本文的思想
- 单个解码器能生成一组多样和互补的解
- 不强制第一个节点的选择,能扩展到其他CO问题上(因此本文探索了CVRPTW,TW问题不能强制第一个节点的选择)
方法
总览
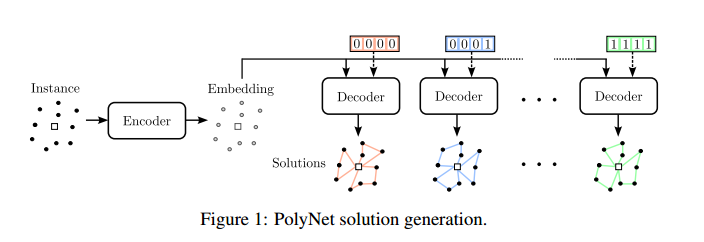
追求多样性从根本上讲是增强探索能力的一种手段,从而提高解决方案的质量。PolyNet 不仅在测试时提升性能(在测试时为每种策略采样多个解决方案并只保留最佳的一个),还在训练期间改善了探索能力。
PolyNet 旨在使用单一神经网络学习 $ K $ 种不同的解决方案策略 $ \pi_1, \ldots, \pi_K $ 。为了实现这一目标,通过额外的输入 $ v_1, \ldots, v_K $ 来条件化解决方案的生成过程,这些输入定义了应该使用哪种策略来采样解决方案,以便:
\[\pi_1, \ldots, \pi_K = \pi_\theta(\tau_1 | l, v_1), \ldots, \pi_\theta(\tau_K | l, v_K)\]为 $ \lbrace v_1, \ldots, v_K\rbrace $ 使用一组唯一的比特向量。只要网络能够轻松区分这些向量,也可以使用其他表示方法。
上图展示了该模型的整体解决方案生成过程,其中使用大小为 4 的比特向量生成了 $ K = 16 $ 个不同的 CVRP 实例解决方案。
简单来说就是给解码器输入一些比特位,促使解码器生成不同的输出。
训练
在训练过程中,反复地基于 $ K $ 个不同的向量 $ \lbrace v_1, \ldots, v_K\rbrace $ 为实例 $ l $ 采样 $ K $ 个解决方案 $ \lbrace \tau_1, \ldots, \tau_K\rbrace $ ,其中解决方案 $ \tau_i $ 是从概率分布 $ \pi_\theta(\tau_i \mid l, v_i) $ 中采样得到的。为了使网络能够学习 $ K $ 种不同的解决方案策略,采用 Poppy 方案,仅根据 $ K $ 个解决方案中最佳的那个来更新模型权重。假设 $ \tau^* $ 是最佳解决方案,即 $ \tau^* = \arg\min_{\tau_i \in \lbrace \tau_1, \ldots, \tau_K\rbrace } R(\tau_i, l) $ , $ v^* $ 是对应的向量(若有多个解同时最优,则任选其一)。然后,基于以下梯度更新模型:
\[\nabla_\theta L = \mathbb{E}_{\tau^*} \left[ (R(\tau^*, l) - b^\circ) \nabla_\theta \log \pi_\theta(\tau^* | l, v^*) \right]\]其中, $ b^\circ $ 是一个基线。仅根据最佳解决方案来更新模型权重,使得网络能够学习那些不需要在训练集所有实例上都表现出色的专门化策略。尽管这种方法没有明确地强制执行多样性,但它鼓励模型为了优化整体性能而学习多样化的策略。
探索与基线
POMO 通过为每个实例从 $ N $ 个不同的初始状态出发展开 $ N $ 个解决方案来增加探索。这利用了许多 CO 问题解空间中的对称性,从而可以从不同的状态找到最优解。在实践中,这一机制是通过为每个实例的 $ N $ 次展开强制使用不同的初始构造动作来实现的。强制执行多样化的展开不仅能改善探索,还可以将所有 $ N $ 次展开的平均奖励用作基线。然而,当初始动作无法自由选择而不影响解决方案质量时,不应使用这种探索机制。
在 PolyNet 中,我们在训练期间不使用假设解空间对称性的探索机制或基线。相反,我们仅依赖于我们条件式解决方案生成所提供的探索能力,这使我们能够解决更广泛的优化问题。作为基线,我们仅使用实例所有 $ K $ 次展开的平均奖励,即:
\[b^\circ = \frac{1}{K} \sum_{i=1}^K R(\tau_i, l)\]网络架构
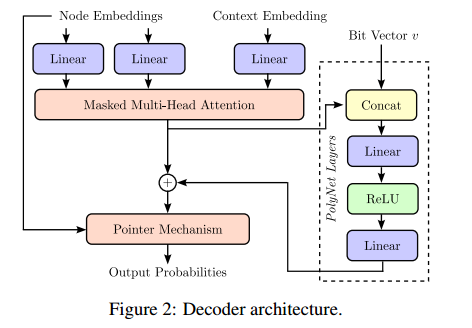
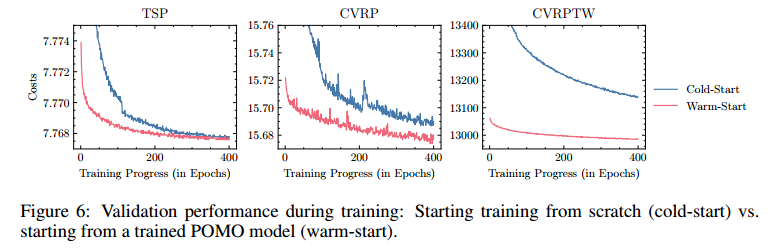
可以从已训练的POMO模型上开始PolyNet的训练。
简单来说就是将位向量直接拼接到多头注意力的输出上。
搜索
在生成解后,用EAS来搜索加强。
实验
设备
- 单个Nvidia A100
问题
- TSP、CVRP、CVRPTW、JSSP
训练
- 从POMO热启动,训练300个epoch,每个epoch有4e8个实例
- K设置为128
评估
- 评估为了公平,k统一设置成8(相比POMO多了8倍的探索)
训练表现
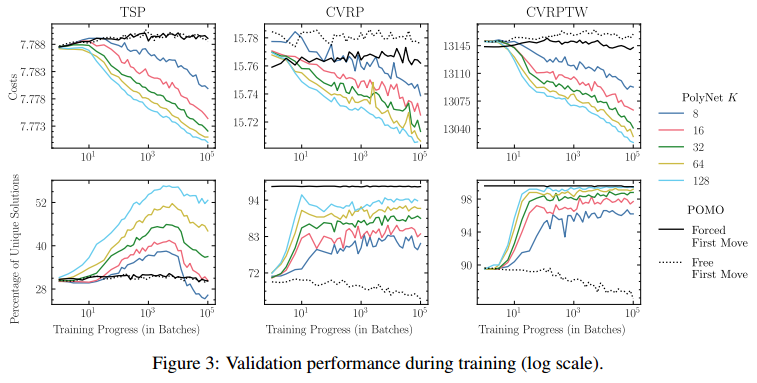
表现
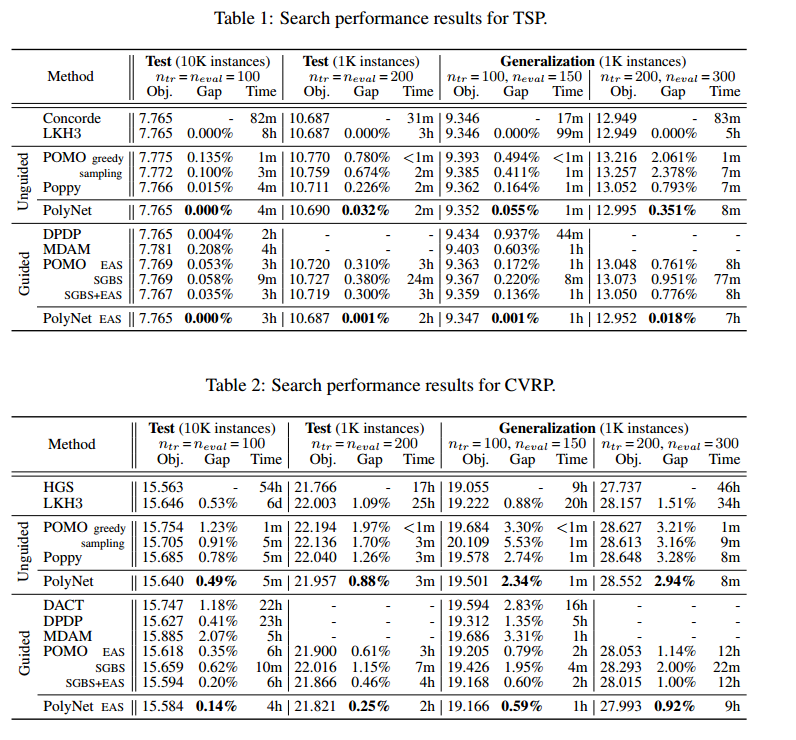
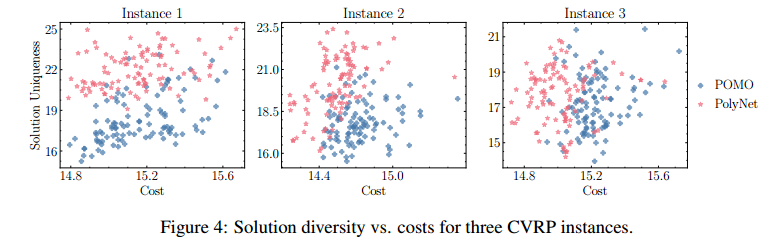
解的多样性
- 解的距离用 broken pairs distance 来评估
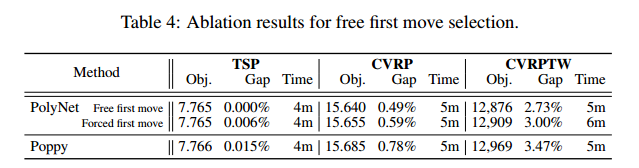
消融实验
- 强制第一步,如POMO
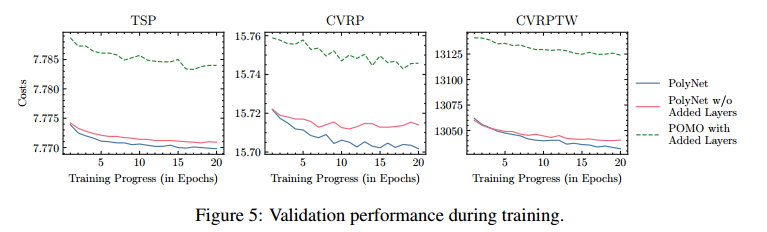
- Added Layers的消融
冷启动和热启动
后搜索的分析
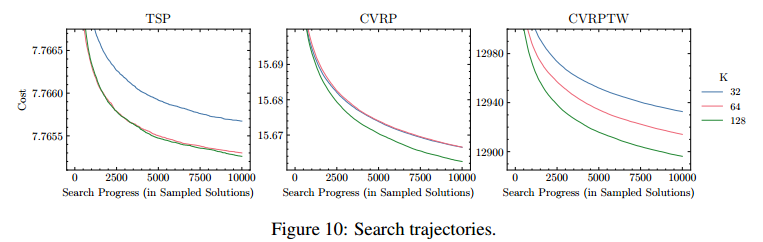
原话是:这一观察结果再次强调了PolyNet发现不同解决方案的能力,使其能够在扩展搜索预算的情况下产生更好的结果。