GLOP: Learning Global Partition and Local Construction for Solving Large-scale Routing Problems in Real-time
AAAI2024

开源:https://github.com/henry-yeh/GLOP
摘要
最近的端到端神经求解器在处理小型路线规划问题上展现出了潜力,但在实时放大到更大规模问题上存在限制。为了解决这个问题,本文提出了GLOP(Global and Local Optimization Policies),这是一个统一的层次化框架,可以有效地扩展到大规模路线规划问题。GLOP将大规模的路线规划问题划分为旅行商问题(TSP),再将TSP划分为最短哈密顿路径问题(SHPP)。本文首次将非自回归神经启发式方法用于粗粒度的问题划分,以及自回归神经启发式方法用于细粒度的路线构建,结合了两者的可扩展性和细致性。实验结果表明,GLOP在大规模路线规划问题上,包括TSP、ATSP、CVRP和PCTSP,都取得了具有竞争力的、最先进的实时性能。
引入
贡献
- 提出了一个通用的GLOP框架,将现有的神经求解器扩展到大规模。这是首次混合NAR和AR的端到端的有效尝试。
- 提出学习全局分区热图来分解大规模路由问题,以一种新的方式利用NAR热图学习。
- 提出了一个通用的实时(A)TSP求解器,可以学习任意大小的(A)TSP的小SHPP(最短哈密顿路径问题)解的构造。
- 第一个有效扩展到100k的神经求解器,目前的SOTA。
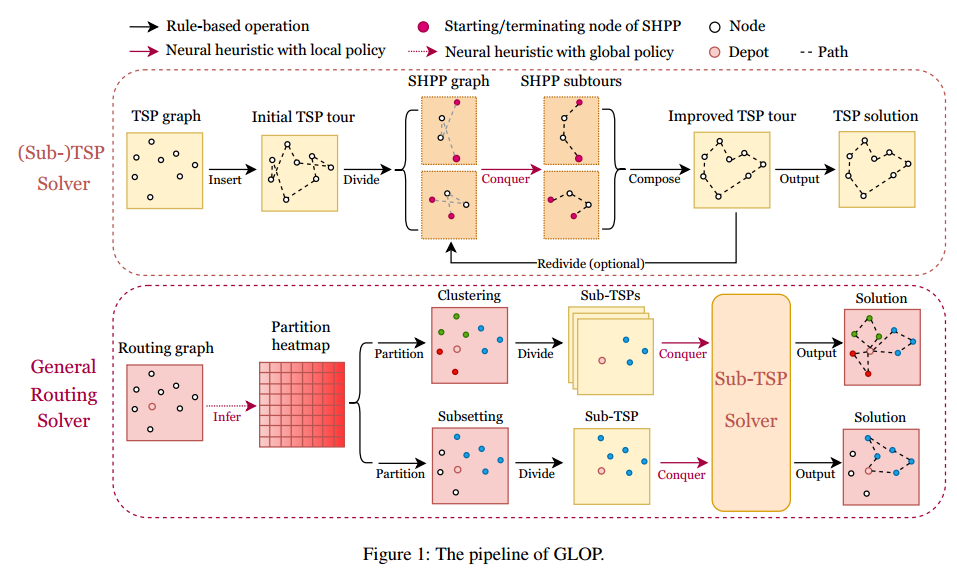
方法总览
方法的设计针对三个具有代表性的问题
- 单独的大规模TSP
- 需要问题划分和求解多个小子TSP的大规模CVRP
- 大规模的PCTSP,需要划分并求解一个大的子TSP
伪代码

子TSP求解器
(省流,先用随机插入获得一个初始解,然后将图分解成多个哈密顿通路,然后通过一个训练的模型重新求解该固定起点和终点的开源TSP。该模型是一个双头模型,即从起点构造一遍路径,和从终点构造一遍路径,推理的时候两个取最好的,训练的时候两者都参与loss计算。)
推理过程
初始化
GLOP使用随机插入法生成初始的TSP路径,一种简单通用的启发式算法,随机选择每个节点的插入成本最小的位置。
GLOP将对这个初始解进行改进,一轮改进称作 revision。
根据一个自回归网络参数化的局部策略,训练 $n$ 个节点的 SHPPs 叫做 Reviser-n。下面是四个顺序步骤。
- 分解:当由 Reviser-n 改进时,包含 $N$ 个节点的完整路径被随机分解为 $\lfloor \frac{N}{n}\rfloor$ 个子路径,每个子路径包含 $n$ 个节点。每两个子路径之间没有重叠。如果有剩余节点,则形成一个“尾部子路径”,在组合阶段之前保持不变。每个子路径对应一个SHPP图,重构子路径等同于解决一个SHPP实例。在重复改进时,随机选择分解位置。
- 转换和增强:为了提高模型输入的可预测性和同质性,对SHPP图应用最小-最大归一化和可选的旋转,将x轴坐标缩放到[0,1]范围,并将y轴的下限设置为0。此外,通过翻转节点坐标来增强SHPP实例,以提升模型性能。
- 使用局部策略解决SHPP:使用可训练的修订器自回归地重构子路径(即解决SHPP实例)。如果任何SHPP解决方案比当前解决方案更差,将被丢弃。
-
组合:将重构的(或原始的)子路径和尾部子路径(如果有)通过连接SHPP的起始/终止节点,按照原始顺序组合成一个改进的完整路径。
- GLOP可以应用多个修订器从不同角度解决问题,也可以在不同点分解路径并重复修订。经过所有修订后,GLOP输出改进的路径作为最终解决方案。值得注意的是,GLOP允许使用一组针对小SHPP训练的模型来解决任意大小的TSP。
用局部策略解决 SHPP
问题描述和动机
SHPP 也被称为开环 TSP。在固定起始/终止节点的情况下,SHPP 的目标是找到访问所有中间节点恰好一次的哈密顿路径的最短长度。
模型
基于注意力模型(AM)参数化局部策略。 局部策略:给定一个 SHPP 实例 s,起始/终止节点分别为 1 和 n,随机局部策略 $ p\theta(\omega_{fd}, \omega_{bd} \mid s) $ 表示构建前向和后向解 $ \omega_{fd} $ 和 $ \omega_{bd} $ 的条件概率。
\[p\theta(\omega_{fd}, \omega_{bd} \mid s) = p\theta(\omega_{fd} \mid s) × p\theta(\omega_{bd} \mid s)\] \[= \prod_{t=1}^{n-2} p\theta(\omega_t \mid s, \omega_{1:t-1}, n) × p\theta(\omega_t \mid s, \omega_{1:t-1}, 1).\]在推理过程中,接受 $ \omega_{fd} $ 和 $ \omega_{bd} $ 中较好的一个,而在训练过程中则同时使用两者。
训练
通过最小化其构造的 SHPP 解决方案的预期长度来训练参数化的局部策略(即修订器):
\[\min L(\theta \mid s)=E_{\omega_{f d}, \omega_{b d} \sim p\theta(\omega_{f d}, \omega_{b d}\mid s)}[f_{S H P P}(\omega_{f d}, s)+f_{S H P P}(\omega_{b d}, s)],\]其中 $f_{S H P P}$ 将 SHPP 解映射到其长度。我们应用基于 REINFORCE 的梯度估计器,使用两个贪婪回滚的平均路径长度作为基线。这种训练算法使每个实例的经验翻倍,并通过权衡两个方向的贪婪回滚来实现更可靠的基线。
两阶段课程学习
根据坐标变换,设计了一个两阶段课程,以提高训练和推理实例之间的同质性和一致性。
动机如下:修订器的输入
- 经过坐标变换后 y 轴上界范围为 0 到 1 的 SHPP 图
- 其前面模块的输出。
因此,课程的第一阶段使用多分布 SHPP 训练修订器,这些 SHPP 的 y 轴上界各不相同;第二阶段则按照推理流程协同微调所有修订器。
通用路由问题求解器
可以通过聚类(如CVRP、mTSP、CARP)或者节点子集(如PCTSP、OP、CSP)将问题分解成多个子TSP或者单个TSP问题来解决。
对于这些一般的问题,GLOP需要设计一个额外的全局分区策略。
作为分区热图的全局策略
分区热图
引入了一个参数化的分区热图 $ H_{\phi}(\rho) = [h_{ij}(\rho)]_{(n+1) \times (n+1)} $ ,其中 $ \rho $ 是包含 $ n + 1 $ 个节点的输入实例,节点 0 作为仓库。 $ h_{ij} \in \mathbb{R}^+ $ 表示节点 $i$ 和 $j$ 属于同一子集的非归一化概率。
模型和输入图
分区热图由一个同构的图神经网络(GNN) $ \phi $ 参数化。输入到模型的是为不同问题专门设计特征的稀疏图。
全局策略
对于节点聚类,GLOP 将所有节点分区为多个子集,每个子集对应一个子 TSP 问题。对于节点子集划分,GLOP 将所有节点分区为两个子集,即待访问子集和其他节点,其中待访问子集形成一个子 TSP 问题。设 $ \pi = \lbrace \pi_r\rbrace _{r=1}^{\mid \pi\mid } $ 表示一个完整的分区, $ \pi_r = \lbrace \pi_{r t}\rbrace _{t=1}^{\mid \pi_r\mid } $ 表示第 $r$ 个子集,包含普通节点和仓库。每个子集以仓库开始和结束,即 $ \pi_{r 1} = \pi_{r \mid \pi_r\mid } = 0 $ 。给定 $ H_{\phi}(\rho) $ ,全局策略通过顺序采样节点来将所有节点分区为 $ \mid \pi\mid $ 个子集,同时满足特定问题的约束条件 $ \Theta $ :
\[p_{\phi}(\pi \mid \rho) = \begin{cases} \prod_{r=1}^{\mid \pi\mid } \prod_{t=1}^{\mid \pi_r\mid - 1} \frac{h_{\pi_{r t}, \pi_{r t+1}}(\rho)}{\sum_{k \in N(\pi_p)} h_{\pi_{r t}, k}(\rho)}, & \text{if } \pi \in \Theta, \\ 0, & \text{otherwise}, \end{cases}\]其中 $ N(\pi_p) $ 是给定当前部分分区的可行操作集。
训练算法
训练全局策略使其输出的分区能够在解决子 TSP 问题后带来最佳的最终解决方案。对于每个实例 $ \rho $ ,训练算法推断分区热图 $ H_{\phi}(\rho) $ ,并行采样子节点分区,将采样的分区输入 GLOP 以获得子 TSP 解决方案,然后优化预期的最终性能:
\[\min L(\phi\mid \rho)=E_{\pi \sim p_{\phi}(\pi\mid \rho)}\left[\sum_{r=1}^{\mid \pi\mid } f_{TSP}(GLOP_{\theta}(\pi_r, \rho))\right],\]其中 $ f_{TSP} $ 将子 TSP 解映射到其路径长度,$GLOP_\theta$ 使用训练有素的局部策略生成子 TSP 解决方案。应用 REINFORCE 算法,以相同实例采样解的平均奖励作为基线。基线分别针对训练批次中的每个实例进行计算。GLOP 的子 TSP 解决方案(即 $GLOP_\theta$)由于其并行性和可扩展性,使得我们的全局策略能够在大规模问题上进行高效训练。
适用性
大多路由问题可以分层化,设计节点聚类或者节点子集。
对于复杂约束,给不可行解的reward分配一个很大的负值。
实验
基准问题
- TSP 500\1k\10k\100k,真实世界数据集(小于1000,坐标归一化)
- ATSP
- CVRP 1k\2k\5k\7k
- PCTSP 500\1k\5k,$K^n$ 分别设置成 9\12\20,$\beta_i$ 是 0 到 $3\frac{K^n}{n}$ 的标准分布。
设备
- 12-core Intel(R) Xeon(R) Platinum 8255C CPU and an NVIDIA RTX 3090
大规模TSP
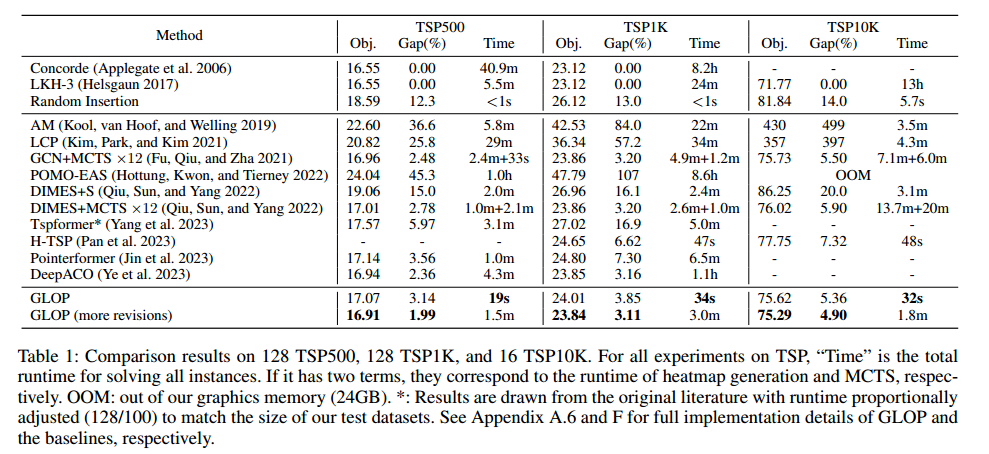
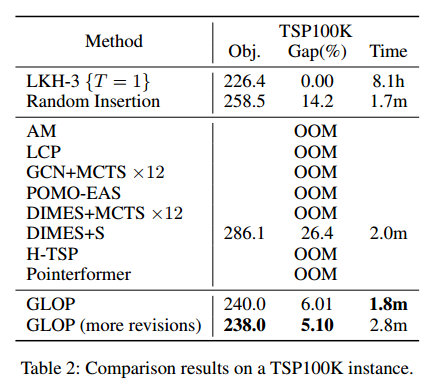
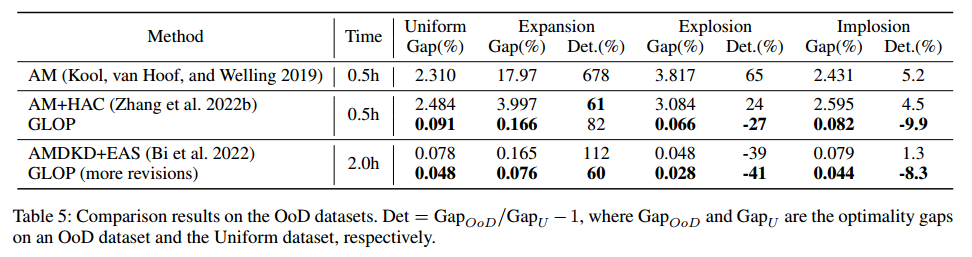
TSP100上的多分布
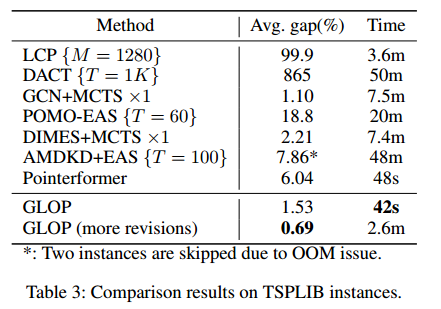
TSPLIB 真实世界数据集
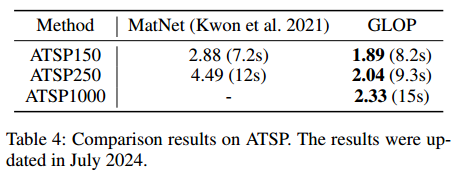
ATSP
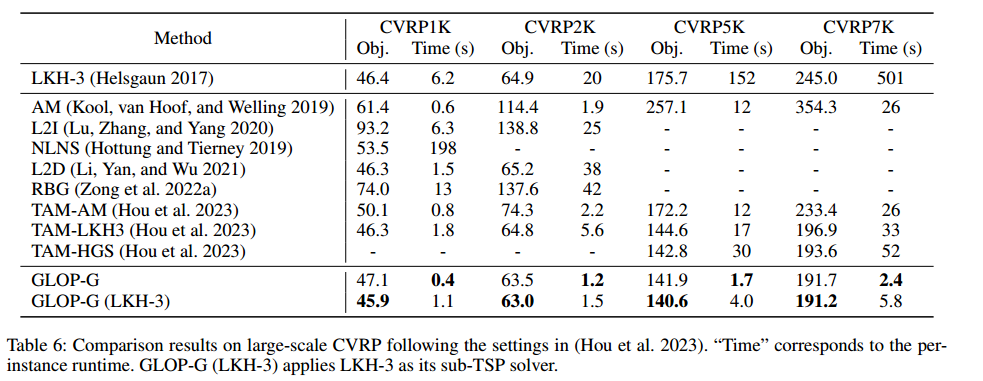
大规模CVRP
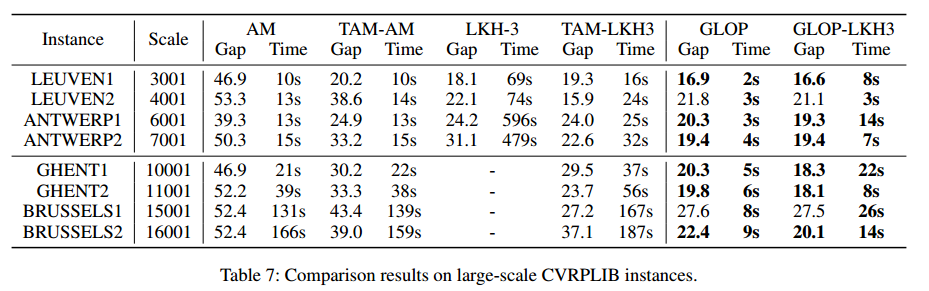
CVRPLIB 真实世界数据集
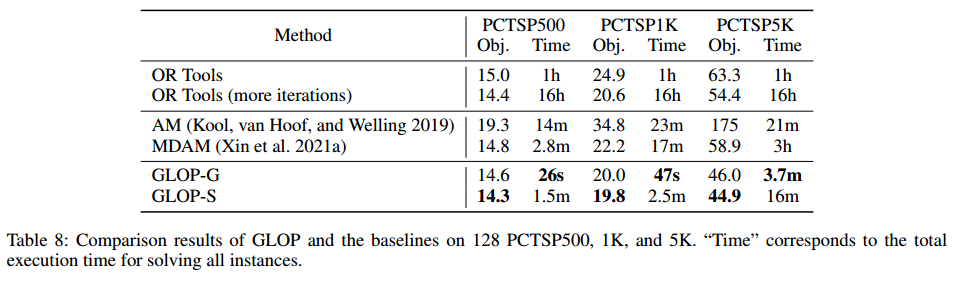
PCTSP
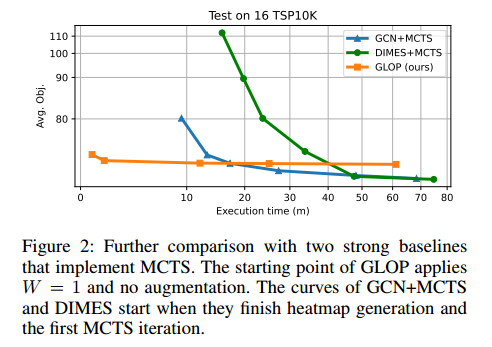
baseline+MCTS
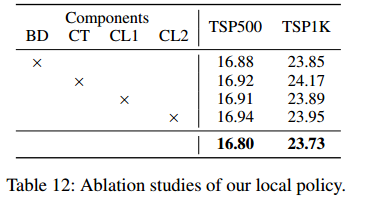
消融实验
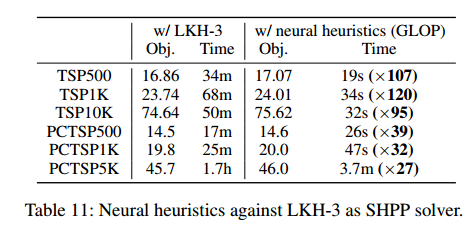
- 将SHPP神经求解器换成LKH
- 双向解码(BD)、坐标变换(CT)、两阶段课程学习(CL1、CL2)
- 全局策略,看表6的GLOP-G(LKH3)和TAM-LKH3,索命NAR全局策略优于AR划分策略