偏好优化理论基础
BT模型
BT模型是一种用于表示实例、团队或对象之间成对比较结果的概率模型。它估计了排序关系 $i \succ j$ 为真的概率,其中符号 $\succ$ 表示偏好或排序关系,例如实例 $i$ 被偏好于 $j$。
BT 模型的计算如下所示,其中两个竞争者的正向强度分别表示为 $\lambda_1$ 和 $\lambda_2$,$r_{1,2}$ 表示第一个竞争者在比较中获得更高排名的概率。
\[r_{12}=\frac{\lambda_{1}}{\lambda_{1}+\lambda_{2}}\]定义 $d_{12}=\ln\lambda_{1}-\ln\lambda_{2}$,它表示两个竞争者强度的对数差异。上式可以改写成下式,其中 $\text{sech}(\cdot)$ 表示双曲正割函数。这种关系表明,偏好概率 $r_{12}$ 仅取决于 $d_{12}$。
\[r_{12}=\frac{1}{4}\int_{-(\ln\lambda_{1}-\ln\lambda_{2})}^{\infty}\text{sech}^{2}(y/2)dy=\frac{1}{4}\int_{-d_{12}}^{\infty}\text{sech}^{2}(y/2)dy\]人类偏好建模
根据 BT 模型,人类偏好分布 $p^\ast$ 如下所示,其中 $r^\ast$ 是某种潜在的奖励模型,$r^\ast(x, y)$ 表示给定输入提示 $x$ 时对响应 $y$ 的奖励,$\sigma(\cdot)$ 是 Sigmoid 函数。变量 $x$、$y_1$ 和 $y_2$ 来自偏好数据集 $D = \lbrace x^i, y^i_1, y^i_2\rbrace$,其中 $y_1$ 是被偏好的响应,$y_2$ 是不被偏好的响应。项 $\exp(r^\ast(x, y))$ 表示遵循的响应强度 $\lambda$,承认奖励可能是负数。
\[p^{\ast}(y_{1}\succ y_{2}\mid x)=\frac{\exp(r^{\ast}(x,y_{1}))}{\exp(r^{\ast}(x,y_{1}))+\exp(r^{\ast}(x,y_{2}))}=\sigma(r^{\ast}(x,y_{1})-r^{\ast}(x,y_{2}))\]随后,可以使用最大似然估计方法训练一个反映人类偏好的奖励模型。
\[\max_{\theta}\mathbb{E}_{(x,y_{1},y_{2})\sim D}[\log\sigma(r_{\theta}(x,y_{1})-r_{\theta}(x,y_{2}))]\](个人理解,$r^\ast$ 是 $\lambda$ 的量化,而 $\exp$ 是为了防止奖励是负数,通过 $\exp$ 推理出了 sigmoid 的形式,最后 $\log$ 是最大似然估计的的训练方法)
直接偏好优化 (DPO)
在 RLHF 中,目标是在 KL 散度约束下最大化奖励的期望。
\[\max_{\pi_{\theta}}\mathbb{E}_{x\sim D,y\sim\pi_{\theta}(y\mid x)}[r_{\psi}(x,y)]-\beta\text{KL}(\pi_{\theta}(y\mid x)\parallel\pi_{\text{ref}}(y\mid x))\]这个问题的最优解满足以下关系式:
\[r(x,y)=\beta\log\frac{\pi^{\ast}(y\mid x)}{\pi_{\text{ref}}(y\mid x)}+\beta\log Z(x)\]其中 $Z(x)=\sum_{y}\pi_{\text{ref}}(y\mid x)\exp(\frac{1}{\beta}r(x,y))$ 仅依赖于提示 $x$。通过将这种关系整合到最大似然估计中,可以得到 DPO 的损失函数,如下所示,但它无法处理平局偏好数据。
\[L_{\text{DPO}}(\pi_{\theta};\pi_{\text{ref}})=-\mathbb{E}_{(x,y_{1},y_{2})\sim D}[\log\sigma(\beta\log\frac{\pi_{\theta}(y_{1}\mid x)}{\pi_{\text{ref}}(y_{1}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{2}\mid x)}{\pi_{\text{ref}}(y_{2}\mid x)})]\]TODO: Enhancing LLM Alignment with Ternary Preferences
美团
ICLR 2025
开源:实施细节和数据集可以在www.example.com中找到https://github.com/XXares/TODO。
摘要
将大型语言模型(LLM)与人类意图对齐对于提高其在各种任务中的性能至关重要。标准对齐技术,例如直接偏好优化(DPO),通常依赖于二进制BradleyTerry(BT)模型,该模型难以捕获人类偏好的复杂性-特别是在存在噪声或不一致标签和频繁关系的情况下。为了解决这些限制,我们引入了Tie-rank Oriented BradleyTerry模型(TOBT),它是BT模型的扩展,明确地包含了关系,使得偏好表示更加细致入微。在此基础上,我们提出了Tie-rank Oriented Direct Preference Optimization(TODO),一种新的比对算法,利用TOBT的三元排序系统来改善偏好比对。在对Mistral-7 B和Llama 3的评估中,8B模型中,TODO在分布内和分布外数据集的建模偏好方面始终优于DPO。使用MT Bench和Piqa、ARC-c和MMLU等基准进行的其他评估进一步证明了TODO的上级对齐性能。值得注意的是,TODO在二元偏好对齐方面也显示出了强大的结果,突出其多功能性和更广泛地集成到LLM对齐的潜力。
简要介绍
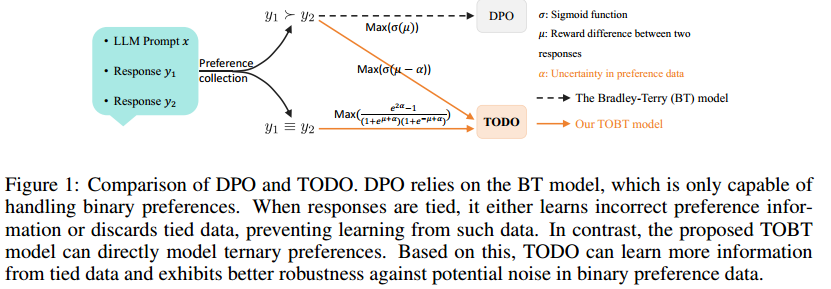
出发点:
- 目前的偏好优化无法处理平局
工作(引入平局):
- TOBT模型(详细推导略)
假设 $r_{12}>\alpha$ 才算赢,那么平局的概率就是 $1-r_{12}-r_{21}$。
$d_{12}$ 表示两个实例之间的偏好差异,$d_{12} > 0$ 意味着第一个实例更受偏好。为了处理平局,通过引入一个正数 $\alpha$ 来提高比较的要求,然后偏好关系由 $d_{12} > \alpha$ 确定。也就是说,排名概率 $r_{12}$ 变为:
\[r_{12} = \frac{1}{4} \int_{-(\ln \lambda_{1} - \ln \lambda_{2}) + \alpha}^{\infty} \text{sech}^{2}\left(\frac{y}{2}\right) dy\]然后,两个实例之间存在平局关系的概率为 $1 - r_{12} - r_{21}$,记作 $r_{(12)}$,可以表示:
\[r_{(12)} = \frac{1}{4} \int_{-(\ln \lambda_{1} - \ln \lambda_{2}) + \alpha}^{(\ln \lambda_{1} - \ln \lambda_{2}) - \alpha} \text{sech}^{2}\left(\frac{y}{2}\right) dy\]TOBT 模型可以表示,其中 $\phi = \exp(\alpha)$ 且 $\phi > 1$。详细的推导过程略。
\[r_{12} = \frac{\lambda_{1}}{\lambda_{1} + \phi \lambda_{2}}\] \[r_{(12)} = \frac{\lambda_{1} \lambda_{2} (\phi^{2} - 1)}{(\lambda_{1} + \phi \lambda_{2})(\phi \lambda_{1} + \lambda_{2})}\]- 带平局的人类偏好分布(详细推导略)
带平局的人类偏好分布 $p^{\ast}$ 可以表示。
\[p^{\ast}(y_{1} \succ y_{2} \mid x) = \frac{\exp(r^{\ast}(x, y_{1}))}{\exp(r^{\ast}(x, y_{1})) + \phi \exp(r^{\ast}(x, y_{2}))}\] \[p^{\ast}(y_{1} \equiv y_{2} \mid x) = \frac{\exp(r^{\ast}(x, y_{1})) \exp(r^{\ast}(x, y_{2})) (\phi^{2} - 1)}{\left(\exp(r^{\ast}(x, y_{1})) + \phi \exp(r^{\ast}(x, y_{2}))\right)\left(\exp(r^{\ast}(x, y_{2})) + \phi \exp(r^{\ast}(x, y_{1}))\right)}\]第一条表示根据 TOBT 模型,将 $y_{1}$ 视为优选响应而 $y_{2}$ 视为非优选响应的可能性。目标函数 $L_{p}^{\text{TODO}}$ 可以写成下式,其中 $\mu = r_{\theta}(x, y_{1}) - r_{\theta}(x, y_{2})$ 表示两个响应 $y_{1}$ 和 $y_{2}$ 的奖励差异。由于隐式奖励 $r_{\theta}(x, y)$ 中的 $Z(x)$ 仅依赖于 $x$,$\mu$ 的差异结果可以等价地表示为 $\mu = \beta \log \frac{\pi_{\theta}(y_{1}\mid x)}{\pi_{\text{ref}}(y_{1}\mid x)} - \beta \log \frac{\pi_{\theta}(y_{2}\mid x)}{\pi_{\text{ref}}(y_{2}\mid x)}$。$L_{p}^{\text{TODO}}$ 中的上标 $p$ 表示当一对响应表现出明确偏好而非平局时,TODO 的目标函数。
\[L_{p}^{\text{TODO}}(\pi_{\theta}; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_{1}, y_{2}) \sim D}[\log \sigma(\mu - \alpha)]\]第二条表示根据 TOBT 模型,将成对响应 $y_{1}$ 和 $y_{2}$ 视为平局的可能性。目标函数 $L_{t}^{\text{TODO}}$ 可以写成下式。$L_{t}^{\text{TODO}}$ 中的上标 $t$ 表示这代表当一对响应平局时 TODO 的目标函数。
\[L_{t}^{\text{TODO}}(\pi_{\theta}; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_{1}, y_{2}) \sim D}\left[\log \frac{\exp(2\alpha) - 1}{(1 + \exp(\mu + \alpha))(1 + \exp(-\mu + \alpha))}\right]\]给定一个偏好数据集 $(x_{i}, y_{i1}, y_{i2}, I_{i}) \in D$,指示符 $I_{i}$ 。具体来说,$I_{i} = 1$ 表示对相同提示 $x$ 的两个响应之间存在明确的偏好或质量差异,而 $I_{i} = 0$ 表示两个响应 $y_{i1}$ 和 $y_{i2}$ 是平局。然后,TODO 的最终损失函数 $L_{\text{TODO}}$ 可以表示。
\[I_{i} = \begin{cases} 1, & y_{i1} \equiv y_{i2}, \\ 0, & y_{i1} \succ y_{i2}. \end{cases}\] \[L_{\text{TODO}} = (1 - I)L_{p}^{\text{TODO}} + I L_{t}^{\text{TODO}}\]- 不同偏好对对TODO的影响
对于具有明确偏好的成对数据的梯度更新,引入了一个较小的正值 $\alpha$,与 DPO 相比,当奖励差异被误估时,这会导致更显著的权重调整。这种改进减少了窄奖励边缘的噪声,使 TODO 能够更有效地学习不同的偏好,同时增强优选响应 $y_{1}$ 的可能性,并降低非优选响应 $y_{2}$ 的可能性。
\[\nabla_{\theta} L_{p}^{\text{TODO}}(\pi_{\theta}; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_{1}, y_{2}) \sim D}\left[\beta \sigma(-\mu + \alpha) \left(\nabla_{\theta} \log(\pi(y_{1}\mid x)) - \nabla_{\theta} \log(\pi(y_{2}\mid x))\right)\right]\]对于成对平局数据的梯度更新,$G(\mu) = \frac{\exp(-\mu + \alpha) - \exp(\mu + \alpha)}{(1 + \exp(-\mu + \alpha))(1 + \exp(\mu + \alpha))}$ 随着 $\mu$ 的增加而单调递减,且 $G(0) = 0$。当 $\mu = 0$ 时,两个响应获得相同的奖励,如果 DPO 更新策略模型方式不变,降低非优选响应 $y_{2}$ 的可能性,可能丢弃有价值的信息。相比之下,TODO 不更新任何参数,以保持平局响应之间的一致偏好对齐。
当估计的平局响应的奖励差异为 $\mu > 0$ 时,表明 $y_{1}$ 的奖励高于 $y_{2}$,TODO 的梯度更新策略将降低 $y_{1}$ 的可能性并提高 $y_{2}$ 的可能性。相反,如果 $\mu < 0$,更新将提高 $y_{1}$ 的可能性并降低 $y_{2}$ 的可能性,确保平局响应之间保持偏好一致性。
\[\nabla_{\theta} L_{t}^{\text{TODO}}(\pi_{\theta}; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_{1}, y_{2}) \sim D}\left[ G(\mu) \nabla_{\theta} \log(\pi(y_{1}\mid x)) + G(-\mu) \nabla_{\theta} \log(\pi(y_{2}\mid x)) \right]\]