DIFUSCO: Graph-based Diffusion Solvers for Combinatorial Optimization
nips23
Carnegie Mellon University
开源:Edward-Sun/DIFUSCO: Code of NeurIPS paper: arxiv.org/abs/2302.08224
摘要
基于神经网络的组合优化(Combinatorial Optimization, CO)方法在解决各种 NP 完全(NPC)问题方面显示出良好前景,且无需依赖手工设计的领域知识。本文通过提出一种新颖的基于图的扩散框架,称为 DIFUSCO(Graph-based DIFfUsion Solvers for Combinatorial Optimization),拓展了当前神经求解器在 NPC 问题中的应用范围。
我们的框架将 NPC 问题形式化为离散的 $\lbrace 0,1\rbrace $ 向量优化问题,并利用基于图的去噪扩散模型生成高质量解。我们研究了两种类型的扩散模型:一种是基于高斯噪声的连续扩散模型,另一种是基于伯努利噪声的离散扩散模型。此外,我们设计了一种高效的推理调度策略以提升解的质量。
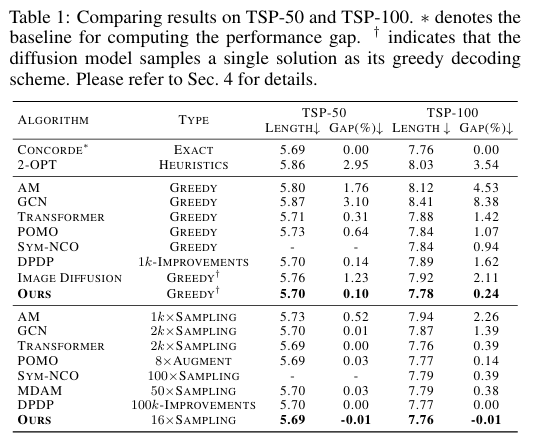
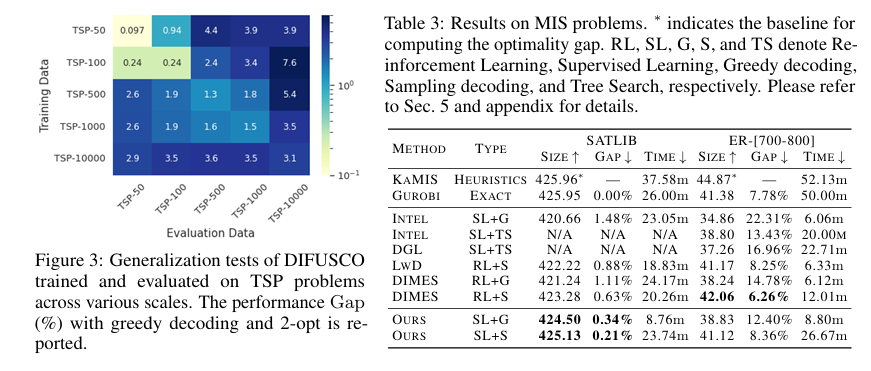
我们在两个经典的 NPC 组合优化问题上评估了我们的方法:旅行商问题(TSP)和最大独立集问题(MIS)。实验结果表明,DIFUSCO 显著优于当前最先进的神经求解器,在 TSP-500 上将性能差距从 1.76% 缩小至 0.46%,在 TSP-1000 上从 2.46% 缩小至 1.17%,在 TSP-10000 上从 3.19% 缩小至 2.58%。对于 MIS 问题,DIFUSCO 在具有挑战性的 SATLIB 数据集上也优于当前最优的神经求解器。
引入
受扩散模型在概率生成任务中成功的启发,提出了一种新颖的方法,名为 DIFUSCO(Graph-based DIFfUsion Solvers for Combinatorial Optimization)。为将扩散模型的迭代去噪过程应用于图结构问题,将每个 NPC 问题形式化为一个离散 $\lbrace 0,1\rbrace $ 向量优化问题,其中每个变量表示图中某个节点或边是否被选中。然后,我们使用基于消息传递的图神经网络(GNN)对问题实例图进行编码,并对被扰动的变量进行去噪。
该图-based 扩散模型从新的角度克服了以往神经 NPC 求解器的局限性:
- 并行推理:DIFUSCO 可在远少于 $N$ 步的去噪步骤中并行推理所有变量,避免了自回归方法的序列生成瓶颈;
- 多模态建模:通过迭代去噪,DIFUSCO 能够建模多峰分布,缓解了非自回归方法表达能力不足的问题;
- 稳定训练:DIFUSCO 使用监督学习方式进行去噪训练,避免了强化学习方法在训练扩展性上的困难。
在 DIFUSCO 框架中研究了两种扩散建模方式:
- 连续扩散模型:使用高斯噪声;
- 离散扩散模型:使用伯努利噪声。
系统比较了这两种建模方式,发现离散扩散模型显著优于连续扩散模型。本文还设计了一种有效的推理策略,进一步提升了离散扩散模型的生成质量。
最终,证明了同一种图神经网络架构——即各向异性图神经网络(Anisotropic Graph Neural Network, AGNN)——可以作为两个不同 NPC 问题(TSP 和 MIS)的骨干网络。实验结果表明,DIFUSCO 在多个规模的 TSP 和 MIS 基准数据集上均优于现有的概率型 NPC 求解器。
相关工作
- 自回归构造式启发求解器
- 非自回归构造式启发求解器
- 离散数据的扩散模型
方法
问题定义
将一个组合优化(CO)问题实例 $s$ 的候选解空间定义为 $X_s = \lbrace 0,1\rbrace ^N$,其中每个解 $x \in X_s$ 是一个长度为 $N$ 的二值向量。我们定义目标函数为:
\[c_s(x) = \text{cost}(x, s) + \text{valid}(x, s)\]其中:
- $\text{cost}(x, s)$ 是任务相关的代价函数(例如 TSP 中路径的总长度),通常是 $x$ 的简单线性函数;
- $\text{valid}(x, s)$ 是验证项,若解 $x$ 是可行的,则返回 0,否则返回 $+\infty$。
我们的优化目标是找到一个最优解 $x_s^*$:
\[x_s^* = \arg\min_{x \in X_s} c_s(x)\]该框架适用于多种 NPC 问题。例如:
- 在 TSP 中,$x \in \lbrace 0,1\rbrace ^N$ 表示从 $N$ 条边中选择一个子集,代价为:
其中 $d_i^{(s)}$ 是问题实例 $s$ 中第 $i$ 条边的权重。$\text{valid}(\cdot)$ 确保选中的边构成一个哈密顿回路。
- 在 MIS 中,$x \in \lbrace 0,1\rbrace ^N$ 表示从 $N$ 个节点中选择一个子集,代价为:
$\text{valid}(\cdot)$ 确保选中的节点构成一个独立集(即任意两个节点之间没有边相连)。
概率型神经 NPC 求解器通过定义一个参数化的条件分布 $p_\theta(x\mid s)$ 来最小化期望代价:
\[\mathbb{E}_{x \sim p_\theta(x\mid s)}[c_s(x)]\]通常使用强化学习进行优化。本文中,我们假设每个训练实例 $s$ 都有已知的高质量解 $x_s^*$,因此采用监督学习方式进行训练。设训练集为 $S = \lbrace s_i\rbrace _{i=1}^N$,我们最大化高质量解的似然,损失函数为:
\[\mathcal{L}(\theta) = \mathbb{E}_{s \sim S}[-\log p_\theta(x_s^*\mid s)]\]接下来,我们将介绍如何使用扩散模型对生成分布 $p_\theta(x\mid s)$ 进行建模。为简洁起见,在后文中我们省略条件 $s$,并将 $x_s^*$ 记为扩散模型中的 $x_0$。
DIFUSCO 中的扩散模型
从变分推断的角度来看,扩散模型是一类潜变量模型,其形式为:
\[p_\theta(x_0) := \int p_\theta(x_{0:T}) dx_{1:T}\]其中 $x_1, \dots, x_T$ 是与数据 $x_0 \sim q(x_0)$ 同维度的潜变量。联合分布为:
\[p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta(x_{t-1}\mid x_t)\]这是反向过程(去噪),逐步从噪声中恢复出数据。而前向过程为:
\[q(x_{1:T}\mid x_0) = \prod_{t=1}^T q(x_t\mid x_{t-1})\]逐步将数据加入噪声。训练目标是最小化负对数似然的变分下界:
\[\mathbb{E}[-\log p_\theta(x_0)] \leq \mathbb{E}_q\left[ -\log \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \right] = \mathbb{E}_q\left[ \sum_{t>1} D_{\text{KL}}[q(x_{t-1}\mid x_t, x_0) \\mid p_\theta(x_{t-1}\mid x_t)] - \log p_\theta(x_0\mid x_1) \right] + C\]其中 $C$ 是常数。
离散扩散模型(Discrete Diffusion)
对于使用多项式噪声的离散扩散模型,前向过程定义为:
\[q(x_t\mid x_{t-1}) = \text{Cat}(x_t; p = \tilde{x}_{t-1} Q_t)\]其中:
- $Q_t = \begin{bmatrix} 1-\beta_t & \beta_t \ \beta_t & 1-\beta_t \end{bmatrix}$ 是转移概率矩阵;
- $\tilde{x}_{t-1} \in \lbrace 0,1\rbrace ^{N \times 2}$ 是将原始向量 $x_{t-1} \in \lbrace 0,1\rbrace ^N$ 转换为每行为 one-hot 的形式;
- $\beta_t$ 是噪声强度,满足 $\prod_{t=1}^T (1 - \beta_t) \approx 0$,使得 $x_T$ 接近均匀分布。
$t$ 步边缘分布为:
\[q(x_t\mid x_0) = \text{Cat}(x_t; p = \tilde{x}_0 Q_t), \quad Q_t = Q_1 Q_2 \dots Q_t\]后验分布为:
\[q(x_{t-1}\mid x_t, x_0) = \text{Cat}\left(x_{t-1}; p = \frac{\tilde{x}_t Q_t^\top \odot \tilde{x}_0 Q_{t-1}}{\tilde{x}_0 Q_t \tilde{x}_t^\top} \right)\]训练时,神经网络预测的是干净数据 $\hat{x}_0$,反向过程为:
\[p_\theta(x_{t-1}\mid x_t) = \sum_{\hat{x}_0} q(x_{t-1}\mid x_t, \hat{x}_0) p_\theta(\hat{x}_0\mid x_t)\]连续扩散模型(Continuous Diffusion)
连续扩散模型也可用于离散数据,通过将输入从 $\lbrace 0,1\rbrace $ 映射到 $\lbrace -1, 1\rbrace $:
\[\hat{x}_0 = 2x_0 - 1\]前向过程为:
\[q(\hat{x}_t\mid \hat{x}_{t-1}) = \mathcal{N}(\hat{x}_t; \sqrt{1 - \beta_t} \hat{x}_{t-1}, \beta_t I)\]$t$ 步边缘分布为:
\[q(\hat{x}_t\mid \hat{x}_0) = \mathcal{N}(\hat{x}_t; \sqrt{\bar{\alpha}_t} \hat{x}_0, (1 - \bar{\alpha}_t)I), \quad \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{\tau=1}^t \alpha_\tau\]后验分布为:
\[q(\hat{x}_{t-1}\mid \hat{x}_t, \hat{x}_0) = \mathcal{N}(\hat{x}_{t-1}; \mu, \Sigma)\]训练时,神经网络预测的是未缩放的高斯噪声 $\epsilon_t$:
\[\epsilon_t = \frac{\hat{x}_t - \sqrt{\bar{\alpha}_t} \hat{x}_0}{\sqrt{1 - \bar{\alpha}_t}} = f_\theta(\hat{x}_t, t)\]反向过程为:
\[p_\theta(\hat{x}_{t-1}\mid \hat{x}_t) = q\left(\hat{x}_{t-1} \mid dle\mid \hat{x}_t, \frac{\hat{x}_t - \sqrt{1 - \bar{\alpha}_t} f_\theta(\hat{x}_t, t)}{\sqrt{\bar{\alpha}_t}} \right)\]最终通过阈值化或量化将 $\hat{x}_0$ 转换回 $\lbrace 0,1\rbrace $ 空间。
快速推理调度
扩散模型推理速度的主要瓶颈在于反向过程步数多,每一步都需要一次神经网络前向传播。为加速推理,一种直接方法是减少反向扩散步数,即使用稀疏调度(sparse schedule)。
DDIM 风格快速采样
连续域中的 DDIM(Denoising Diffusion Implicit Models)通过重新定义反向过程为:
\[q(x_{\tau_{i-1}} \mid x_{\tau_i}, x_0)\]其中 $\tau = \lbrace \tau_1, \dots, \tau_M\rbrace $ 是 $[1, T]$ 的一个长度为 $M$ 的单调子序列,满足 $\tau_1 = 1$,$\tau_M = T$,且 $M \ll T$。
我们考虑两种构造 $\tau$ 的策略:
| 调度名称 | 构造方式 | 说明 |
|---|---|---|
| 线性调度 | $\tau_i = \lfloor c \cdot i \rfloor$ | 均匀稀疏采样 |
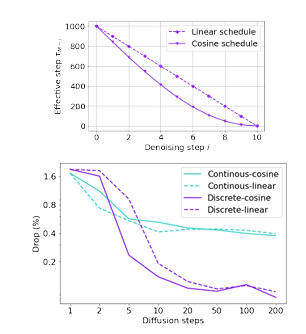
| 余弦调度 | $\tau_i = \lfloor \cos((1 - c \cdot i)\frac{\pi}{2}) \cdot T \rfloor$ | 低密度区采样更多步,提升低噪声阶段精度 |
已验证:余弦调度在离散扩散上显著优于线性调度;在连续扩散上两者相近。因此后续实验默认采用余弦调度。
图-based 去噪网络
网络功能
输入:
- 噪声变量 $x_t \in \lbrace 0,1\rbrace ^N$(或连续 $\hat{x}_t \in \mathbb{R}^N$)
- 问题图实例 $s$(节点坐标 + 边结构)
输出:
- 对干净数据 $x_0$(或 $\hat{x}_0$)的预测
骨干网络 (AGNN)
我们采用 各向异性图神经网络(AGNN)作为统一骨干,原因:
- 同时支持节点变量(MIS)与边变量(TSP)预测;
- 边门控机制可捕捉几何与结构信息;
- 可扩展至百层深度,保持训练稳定。
单层更新规则
设第 $l$ 层:
- $h_i^l$:节点 $i$ 的 $d$ 维特征
- $e_{ij}^l$:边 $ij$ 的 $d$ 维特征
- $t$:去噪时间步(sinusoidal 编码)
则下一层特征为:
\[\tilde{e}_{ij}^{l+1} = P^l e_{ij}^l + Q^l h_i^l + R^l h_j^l\] \[e_{ij}^{l+1} = e_{ij}^l + \text{MLP}_e\Bigl(\text{BN}(\tilde{e}_{ij}^{l+1})\Bigr) + \text{MLP}_t(t)\] \[h_i^{l+1} = h_i^l + \alpha\Bigl(\text{BN}\bigl(U^l h_i^l + \sum_{j \in \mathcal{N}(i)} \sigma(\hat{e}_{ij}^{l+1}) \odot V^l h_j^l\bigr)\Bigr)\]其中:
- $P^l, Q^l, R^l, U^l, V^l \in \mathbb{R}^{d \times d}$:可学习参数
- $\sigma$:sigmoid 门控
- $\alpha$:ReLU 激活
- BN:Batch Normalization
- $\mathcal{N}(i)$:节点 $i$ 的邻居集合
注:AGNN 为边中心消息传递,可同时输出节点嵌入 $\lbrace h_i\rbrace $ 与边嵌入 $\lbrace e_{ij}\rbrace $,天然支持 TSP(边变量)与 MIS(节点变量)两种任务。
输入初始化
| 任务 | 节点特征 $h_i^0$ | 边特征 $e_{ij}^0$ |
|---|---|---|
| TSP | 节点坐标 sinusoidal 编码 | $x_t$ 中对应边 $ij$ 的当前值 |
| MIS | $x_t$ 中节点 $i$ 的当前值 | 全零向量 |
输出头
- 离散扩散:2-神经元分类头 → 输出 $p_\theta(x_0 = 1 \mid x_t, s)$
- 连续扩散:1-神经元回归头 → 输出 $\hat{x}_0$
超参数
所有实验统一采用:
- 12 层 AGNN
- 隐藏维度 256
- Dropout 0.0
- 层间残差连接
解码策略
扩散模型训练完成后,我们从 $p_\theta(x_0\mid s)$ 中采样得到原始变量 $x_0$。然而,概率生成模型无法保证采样结果一定满足 CO 问题的可行性约束(如 TSP 的哈密顿回路、MIS 的独立集)。因此,我们需要为每个任务设计专用解码策略。
热图生成
扩散模型最终输出的是离散变量(离散扩散)或连续变量(连续扩散)。为保留变量置信度信息(即哪些变量更可能被选中),我们将其转换为热图(heatmap):
| 模型类型 | 热图得分计算方式 |
|---|---|
| 离散扩散 | 直接使用最终预测概率 $p_\theta(x_0 = 1 \mid s)$ |
| 连续扩散 | 去掉量化步骤,使用 $0.5(\hat{x}_0 + 1)$ 作为得分 |
与先前非自回归方法不同,DIFUSCO 可通过不同随机种子生成多样化热图,从而支持多模态解空间搜索。
TSP 解码
设热图得分为 $\lbrace A_{ij}\rbrace $,表示边 $(i,j)$ 的置信度。
- 贪心解码 + 2-opt(默认)
- 按得分降序排序所有边;
- 依次加入解中,避免子环/度冲突;
- 最后执行 2-opt 局部搜索进一步优化。
- 蒙特卡洛树搜索(MCTS)
- 以热图为先验,采样 k-opt 动作;
- 模拟、选择、反向传播直至无改进;
- 可支持多热图并行搜索。
MIS 解码
设节点热图得分为 $\lbrace a_i\rbrace $。
贪心解码
- 按 $a_i$ 降序遍历节点;
- 若加入后仍为独立集,则选中;
- 无需后处理:文献指出,即使从随机解出发,图归约 + 2-opt 也能达到近优解。
多解采样
遵循概率 CO 求解器常见做法:
- 用不同随机种子生成 K 张热图;
- 分别解码得到 K 个解;
- 报告最优解(长度最大/最小)。
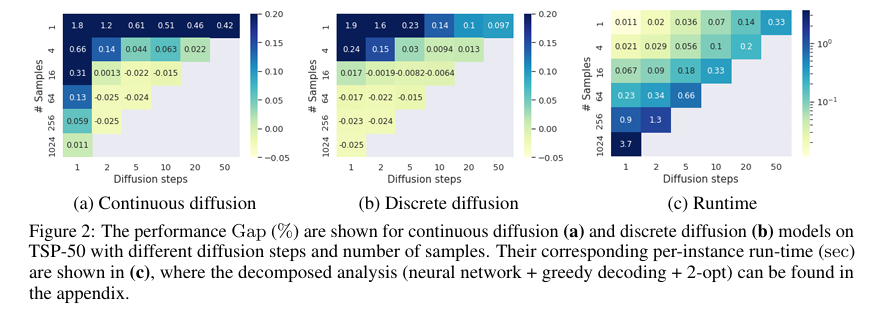
实验表明,增加扩散步数比增加采样数更高效。
训练细节
见原文
实验