ICLR 2026 review阶段,LLM AHD合集一
Generalizable Heuristic Generation Through LLMs with Meta-Optimization
https://openreview.net/forum?id=tIQZ7pVN6S
rating:8444, Accept
现有方法痛点
- 启发式优化器固定:大多数方法使用预设的进化计算(EC)框架,限制了搜索空间的多样性。
- 单任务训练:仅在单一任务上训练,导致泛化能力差,难以应对不同规模或类型的问题。
贡献
- 提出MoH框架: MoH不直接生成启发式算法,而是生成用于生成启发式算法的“元优化器”。通过元学习的方式,MoH不断迭代改进这个元优化器,使其能自适应地生成适用于不同任务的启发式优化器。
- 双层优化结构:
- 外层(Meta-level):元优化器生成多个候选的启发式优化器。
- 内层(Task-level):每个启发式优化器在多个下游任务上生成并优化启发式算法。
- 根据表现最好的启发式优化器更新元优化器,实现自我进化。
- 多任务训练机制: 在训练阶段引入多个不同规模或类型的COP任务,提高元优化器的泛化能力。
- 实验验证: 在TSP(旅行商问题)、BPP(装箱问题)、CVRP(车辆路径问题)等经典组合优化问题上,MoH生成的启发式算法在多个规模上均优于现有的传统方法和其他LLM-based方法。
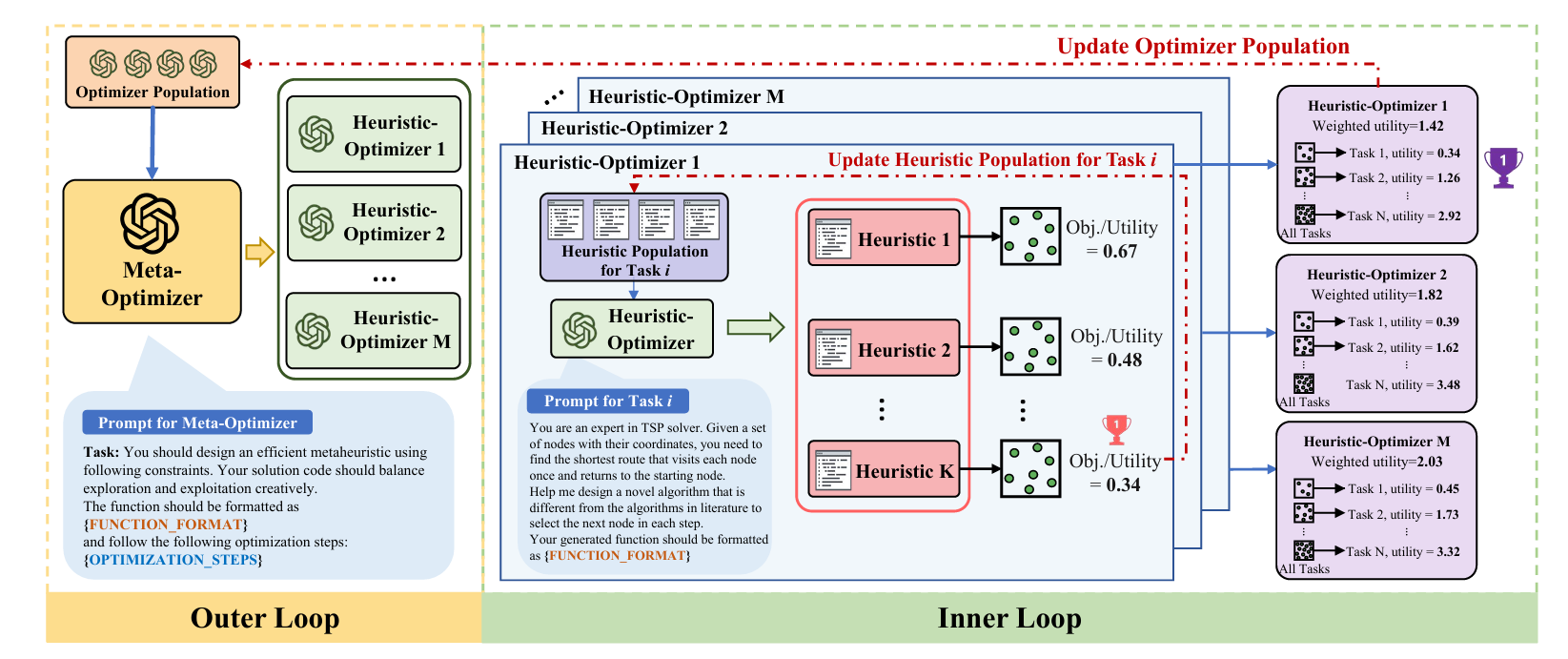
方法省流
现有的方法的框架是种群算法,现在把这个种群算法的框架变成了可以通过LLM设计的启发式。
方法
-
初始化 为每个下游任务$i$初始化一个启发式种群$\mathcal{H}_i$(通过LLM生成多样化启发式代码及自然语言描述),并用种子元优化器$\mathcal{I}_0$初始化优化器种群$\mathcal{P}$。
-
外层循环(优化器设计) 在第$t$轮迭代中,当前元优化器$\mathcal{I}_{t-1}^*$通过(自我)调用产生$M$个候选启发式优化器$\lbrace \mathcal{I}_t^1, \dots, \mathcal{I}_t^M\rbrace $。
-
内层循环(启发式设计) 每个候选启发式优化器$\mathcal{I}_t^j$在所有下游任务上独立演化出$K$个启发式算法,得到$\lbrace \lbrace h_{i,1}^{\mathcal{I}_t^j}, \dots, h_{i,K}^{\mathcal{I}_t^j}\rbrace \rbrace _{i=1}^{N}$。
-
评估与选择 对每个任务$i$选取最优启发式$\tilde{h}_i^{\mathcal{I}_t^j}$,计算该候选优化器的加权总效用:
效用最高的候选优化器成为下一轮元优化器$\mathcal{I}_t^*$。
- 推断阶段 训练完成后,最终元优化器$\mathcal{I}_T^*$可用于新任务(如更大规模问题)。通过若干轮启发式设计,即可快速获得高质量的任务专用启发式算法。
实验
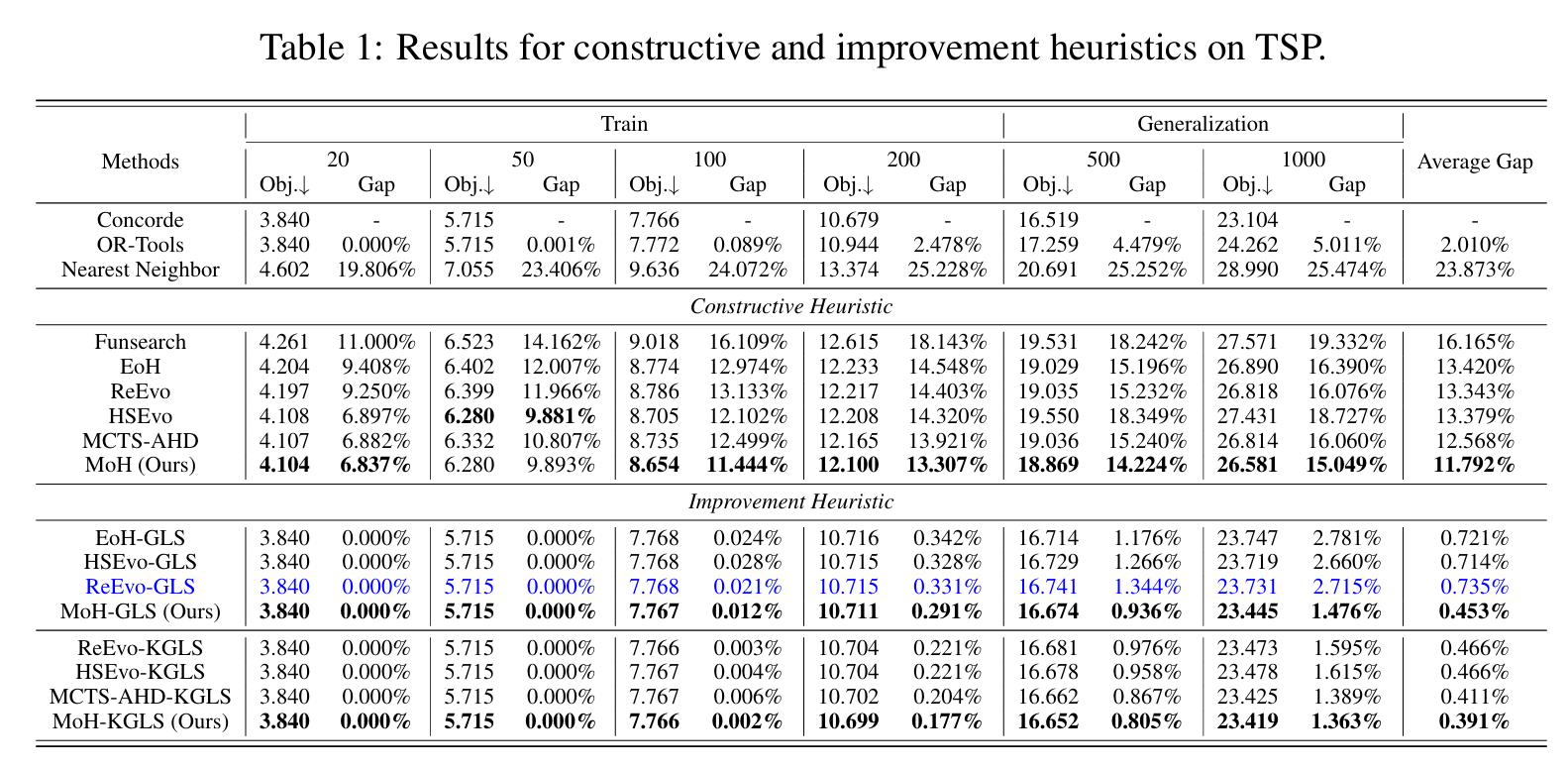
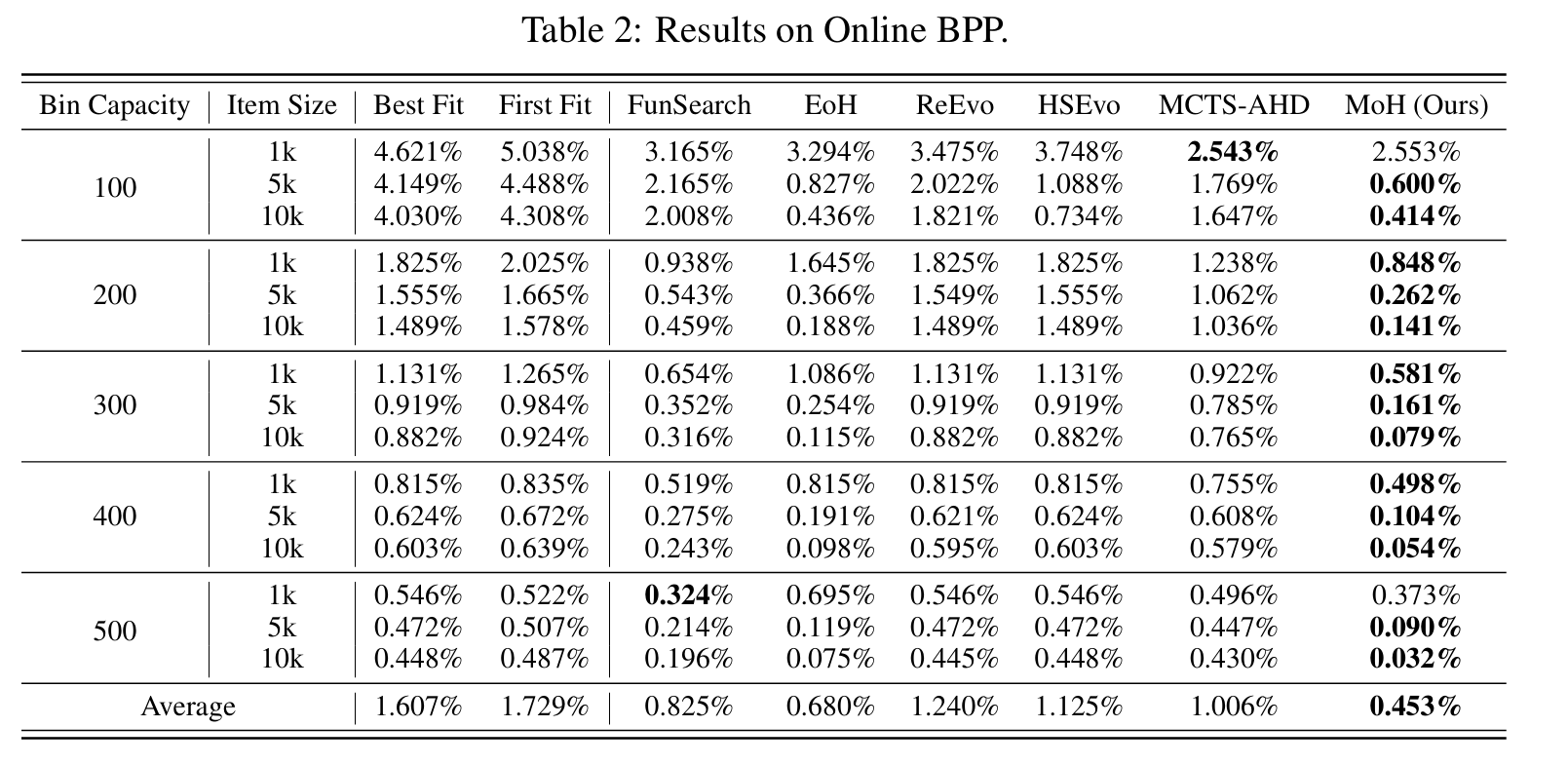
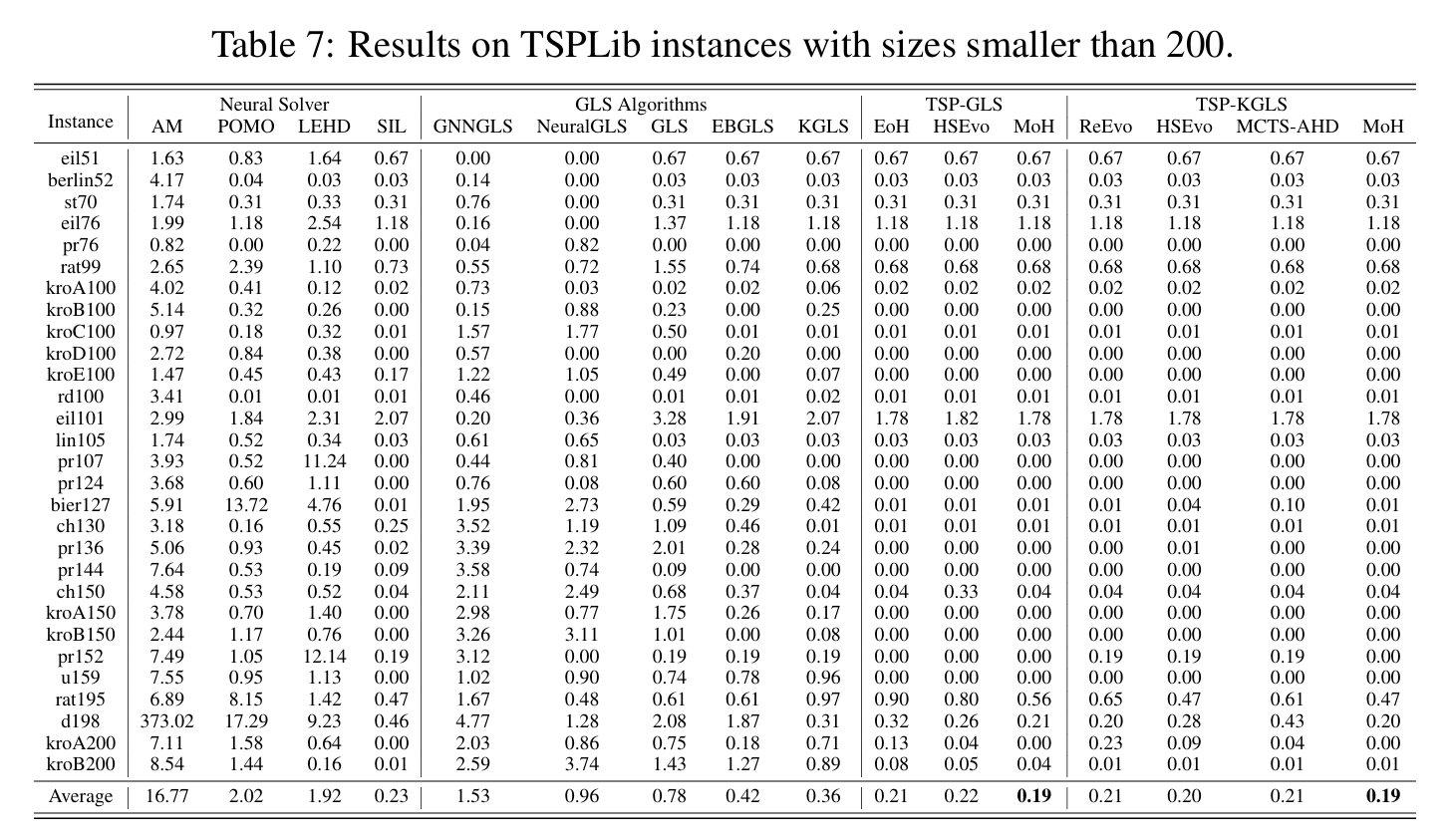
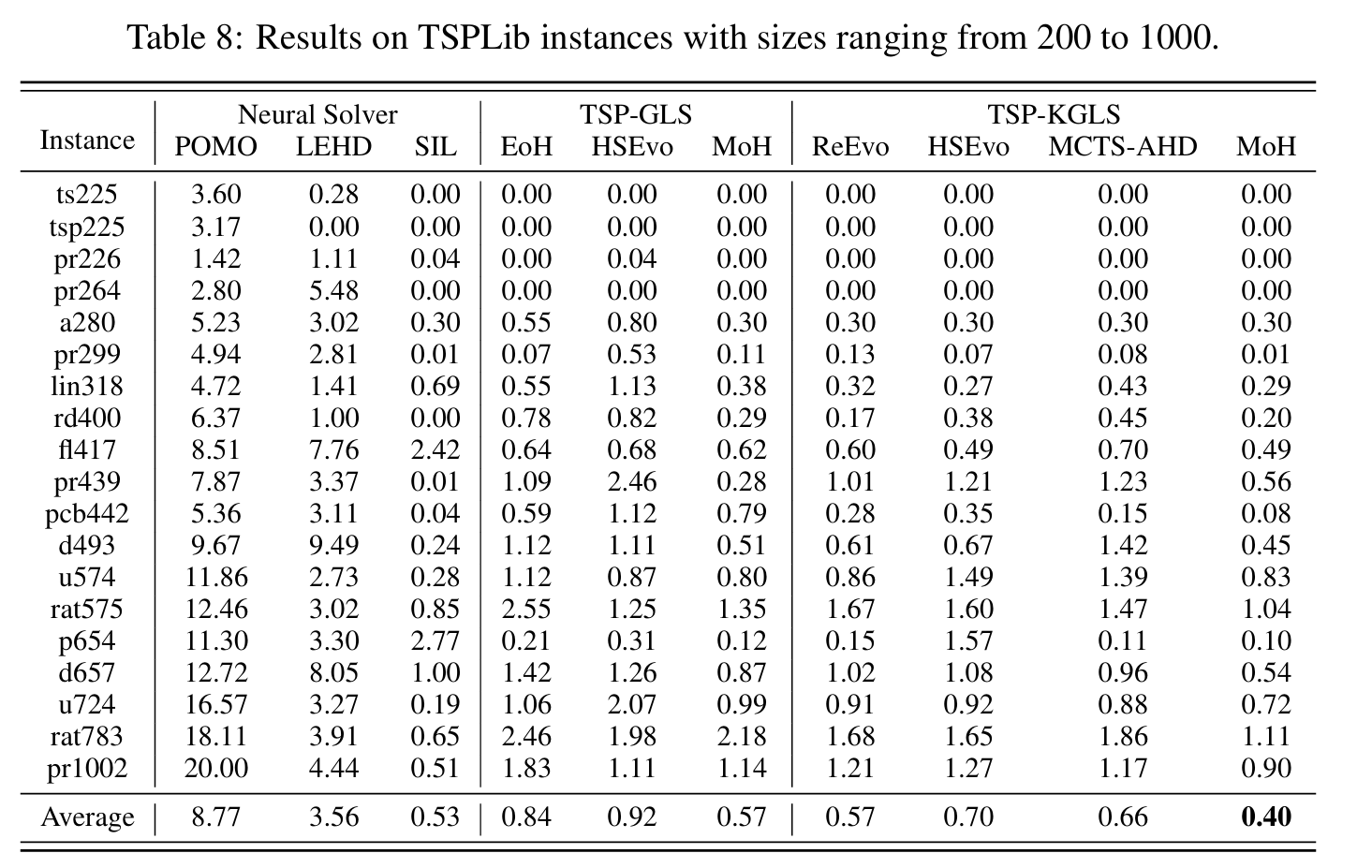
审稿人意见
- 实验结果并无明显改善
- 实验对比并不公平
- 元启发式优化器不还是用进化算法生成的
Rethinking Code Similarity for Automated Algorithm Design with LLMs
https://openreview.net/forum?id=HIUqeO9OOr
rating:6266, Accept
省流:通过代码相似性检测,扩大种群代码多样性。
审稿人意见:相似性检测采用的BehaveSim局限性很大。
CALM: Co-evolution of Algorithms and Language Model for Automatic Heuristic Design
https://openreview.net/forum?id=x6bG2Hoqdf
rating:4828, Accept
痛点
现有基于 LLM 的 AHD 方法仅通过文本提示操控(即“言语梯度”)来引导启发式演化,并未对底层 LLM 本身进行调优,从而错失了基于启发式反馈来提升模型生成能力的机会。
贡献
引入了GRPO对LLM进行微调。
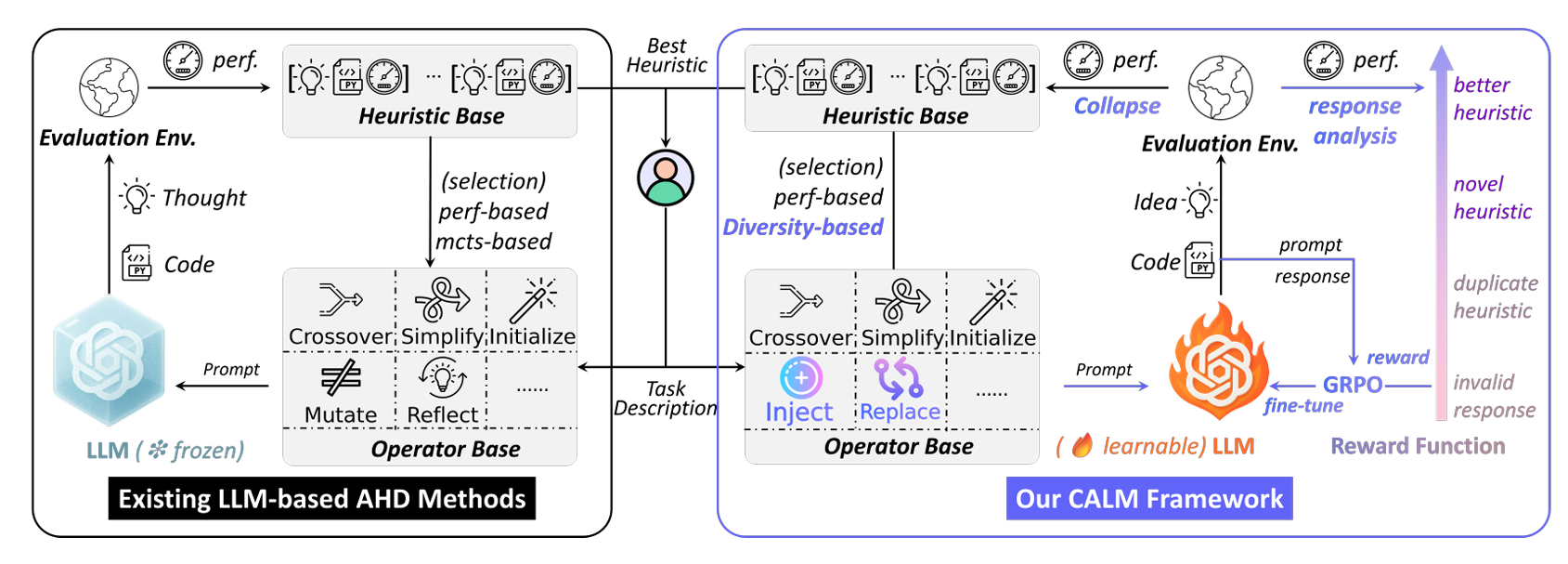
方法
提示生成
CALM 提供五种演化算子:注入(injection)、替换(replacement)、交叉(crossover)、简化(simplification)与初始化(initialization)。除初始化外,所有算子均从当前池中采样一个或多个启发式作为“父代”,生成新提示。下面依次介绍启发式采样策略与各算子细节。
启发式采样策略
-
非交叉算子(注入、替换、简化)按性能排名逆概率采样:
\[P(h) \propto \frac{1}{\mathrm{rank}_p(h)}\]
对启发式 $h$,其被采样概率为其中 $\mathrm{rank}_p(h)$ 为 $h$ 在当前池中的性能排名;排名低于种群规模阈值者概率为 0。
-
交叉算子采用混合策略:
\[\mathrm{div}(h_1, h_2) = \frac{\mid \text{idea\_token}(h_2) \setminus \text{idea\_token}(h_1)\mid }{\mid \text{idea\_token}(h_2)\mid }\]
以 0.5 概率执行性能交叉(双亲均按性能排名采样);
以 0.5 概率执行多样性感知交叉:第一个父代按性能采样,第二个父代按多样性排名逆概率采样。
多样性度量定义为其中 $\text{idea_token}(\cdot)$ 为启发式思路文本的唯一词集合。
细粒度变异算子
- 注入(Injection)
给定一个父代启发式,提示 LLM 向其中注入一个全新组件,并要求在返回的思路中用一句话描述该组件(格式:“The new component … has been introduced.”)。- 全局维护已注入组件描述列表,后续注入必须选择未出现过的组件,以保证多样性。
- 若当前池中个体数少于种群规模,提高注入算子采样权重,加速早期探索。
- 替换(Replacement)
给定父代启发式,提示 LLM 识别并替换某一现有组件。CALM 预定义三类替换指令:- 将实例无关的决策规则改为依赖当前观测的实例相关规则;
- 将人为设定的超参数(常数或静止变量)替换为有理论或实践依据的常数;
- 将对所有候选元素赋予相等或近似相等权重的片段,重写为根据上下文性能差异性地赋予权重的片段。
每次应用替换算子时,随机采样一条指令执行。
多样性感知交叉(Crossover)
交叉提示模板要求 LLM 综合两个父代启发式的优势,生成一个在任何相同实例上表现更优的新算法。通过上述混合采样策略,确保至少一个父代高质量,另一个或高性能、或结构新颖,从而在利用与探索间取得平衡。
简化(Simplification)
随着演化进行,启发式可能累积冗余或过度复杂组件。简化算子提示 LLM 对给定启发式进行蒸馏与精炼,生成更简洁、高效且保留核心思想的版本。
初始化(Initialization)
当池中无任何启发式(未提供种子)时,调用初始化算子,提示 LLM 从零生成一个高效算法;提示模板仅包含问题描述与代码格式要求。
崩溃机制
为什么需要崩溃?
LLM 演化搜索的成功在于:包含更优启发式的提示更容易引导 LLM 生成更优新启发式,形成自我强化循环。然而,这一机制也可能导致近亲繁殖与早熟收敛:种群逐渐被当前最优启发式的微小变体占据,陷入局部最优。
如何崩溃?
当检测到停滞时,CALM 主动重置种群:
- 仅保留两个个体:原始种子启发式 与 当前最优启发式;
- 清空其余所有个体,以二者为种子重新启动演化;
- 在重新填充阶段,暂时放宽选择压力:若池中个体数 < 种群规模,新产生的启发式无论性能如何均被接受,从而给予结构新颖但暂时表现平庸的组件传播与演化机会。
何时崩溃?
当池中个体数达到目标种群规模后,CALM 启动无突破计数器 $c_n$:
- 每轮(一次提示采样 $G$ 个响应)若未产生全局更优启发式,则 $c_n \leftarrow c_n + 1$;
- 否则重置 $c_n \leftarrow 0$。 每轮结束时,以概率
触发崩溃,其中 $\delta_0 \ll 1$ 控制概率增长速度,$C$ 为硬上限。 论文给出期望崩溃轮次近似:
\[\mathbb{E}[c_n \mid \text{collapse}, C > 1/\delta_0] \approx \sqrt{\frac{\pi}{2\delta_0}}\]奖励函数设计
奖励函数为每个 LLM 响应打分,指导 GRPO 更新模型参数。AHD 目标在于可行、新颖且高性能的启发式。为此,我们采用渐进式评分:
-
不可行响应(无法解析为有效启发式) 奖励为负值,上界为 $r_{\mathrm{invalid}} \in (-1,0)$。
-
可行启发式 设 $H$ 为构造提示所用父代启发式集合,$h_{\mathrm{new}}$ 为解析出的新启发式,定义
\[h_{\text{base}}^* = \arg\max_{h \in H} g(h)\]相对性能差距
\[\Delta(h_{\mathrm{new}}, h_{\text{base}}^*) = \mathrm{clip}\left( \frac{\mid g(h_{\mathrm{new}}) - g(h_{\text{base}}^*)\mid }{\min\lbrace \mid g(h_{\mathrm{new}})\mid , \mid g(h_{\text{base}}^*)\mid \rbrace }, 0,1 \right)\]奖励函数定义为
\[r_\phi(q,o \mid h_{\mathrm{new}}, h_{\text{base}}^*) = \begin{cases} \alpha_1 r_{\mathrm{invalid}}, & \exists h \in H, g(h)=g(h_{\mathrm{new}}); \\[4pt] \alpha_2 r_{\mathrm{invalid}} \cdot \Delta, & g(h_{\mathrm{new}}) < g(h_{\text{base}}^*); \\[4pt] 1 + \Delta, & g(h_{\mathrm{new}}) > g(h_{\text{base}}^*). \end{cases}\]其中 $0 < \alpha_2 < \alpha_1 < 1$,确保:
- 复制已有性能得微小负奖励;
- 劣于最优父代得比例负奖励;
- 真正改进得正奖励,且改进幅度越大奖励越高。
实验
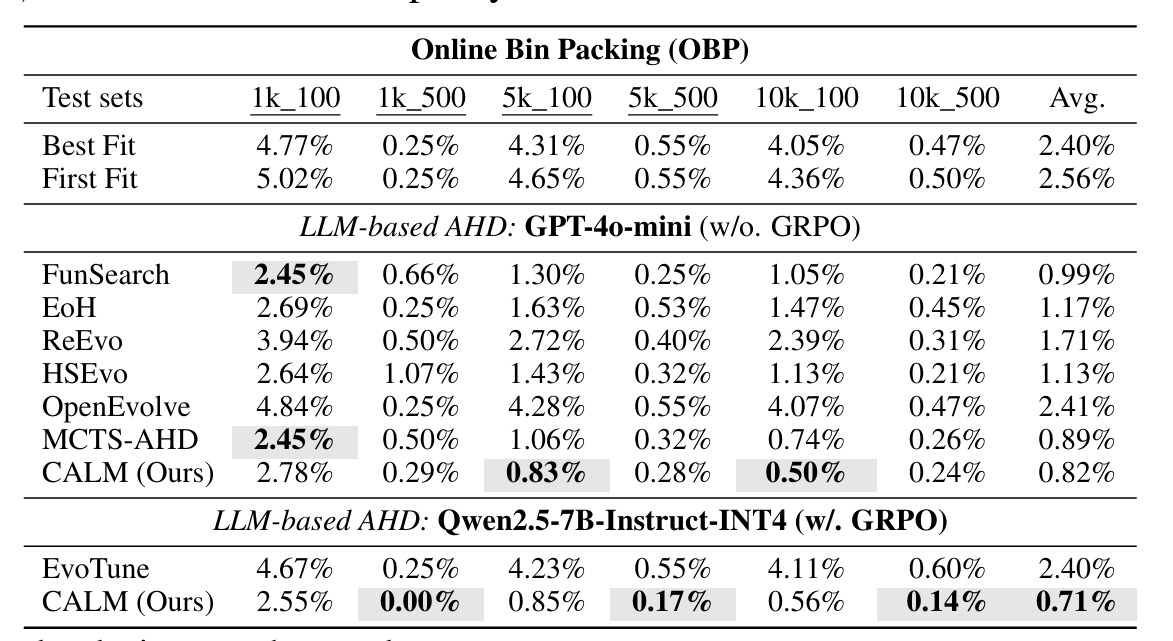
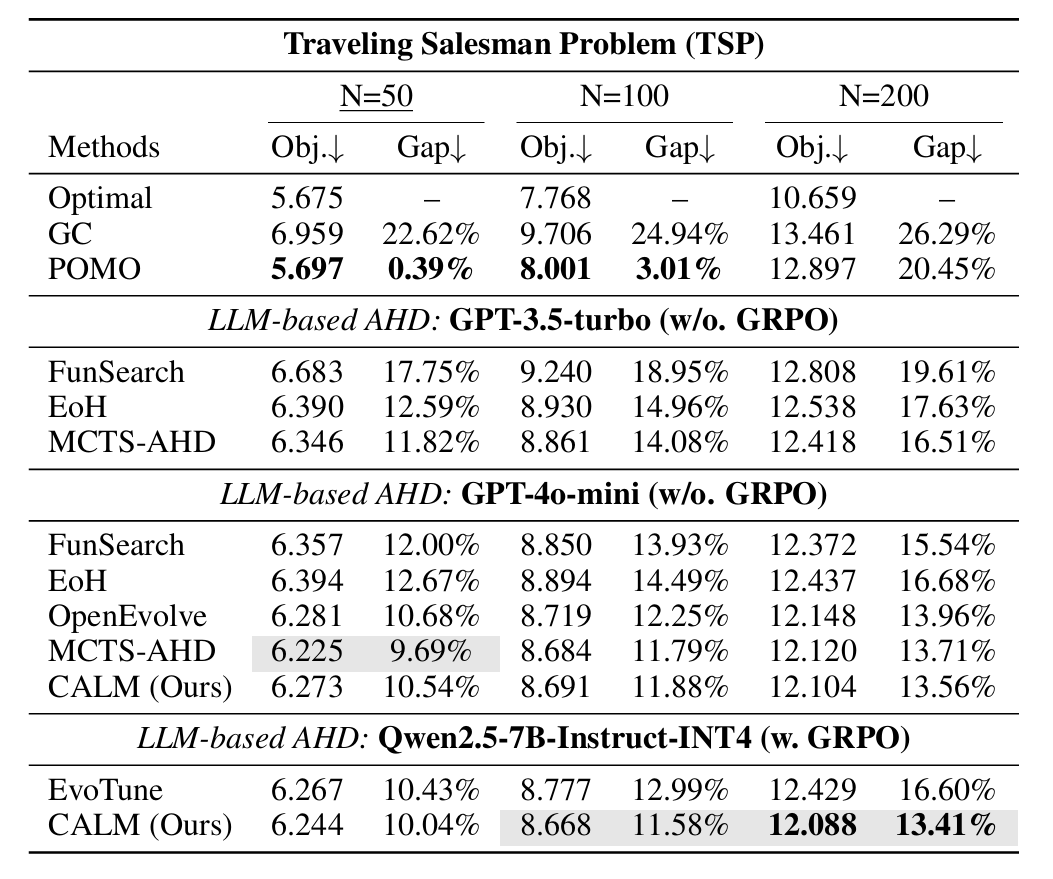
审稿人意见
没什么硬伤。但我个人感觉,实验结果很一般。
Automated Algorithm Design with LLMs: A Benchmark-Assisted Approach to Black-Box Optimization
https://openreview.net/forum?id=ad9BPW5bI6
rating:2442, Reject
动机
- LLM驱动优化的现状:近年来,像 FunSearch、EoH、LLaMEA 等方法已经展示了 LLM 在自动生成优化算法方面的潜力,但大多数方法依赖直觉式 prompt 设计,缺乏对 prompt 各部分的系统性理解。
- 问题:LLM 如何被 prompt 引导生成更好的算法?是否能通过控制 prompt 中的“示例代码”来引导搜索方向?
贡献
- 首次系统性分析 prompt 中各 token 对生成算法的影响 使用 AttnLRP(一种注意力感知的特征归因方法)分析 prompt 中不同部分(如任务描述、策略、示例代码)对生成算法的影响。发现:示例代码(reference code)对生成结果影响最大,远超语言描述或策略说明。
- 提出“基准引导”策略(Benchmark-Guided Approach) 利用已有 benchmark 中的优秀算法代码作为初始示例,引导 LLM 在局部搜索空间内优化算法。方法命名为 BAG(Benchmark-Assisted Guidance)。
- BAG 方法结构
- 采用 (1+1) 精英搜索策略
- 每轮迭代中,LLM 被 prompt 去:
- 精炼当前最优算法(refine)
- 或基于基准算法生成新算法(create)
- 每 q 轮引入一次 benchmark 中的算法进行精炼(q=10 最佳)
审稿人意见
更像是一种直觉,而并非一套方法。
Experience-Guided Reflective Co-Evolution of Prompts and Heuristics for Automatic Algorithm Design
https://openreview.net/forum?id=oD9RwlFqEE
rating:2222,withdraw
人大高瓴
动机
不仅算法进化,prompt也要进化。
贡献
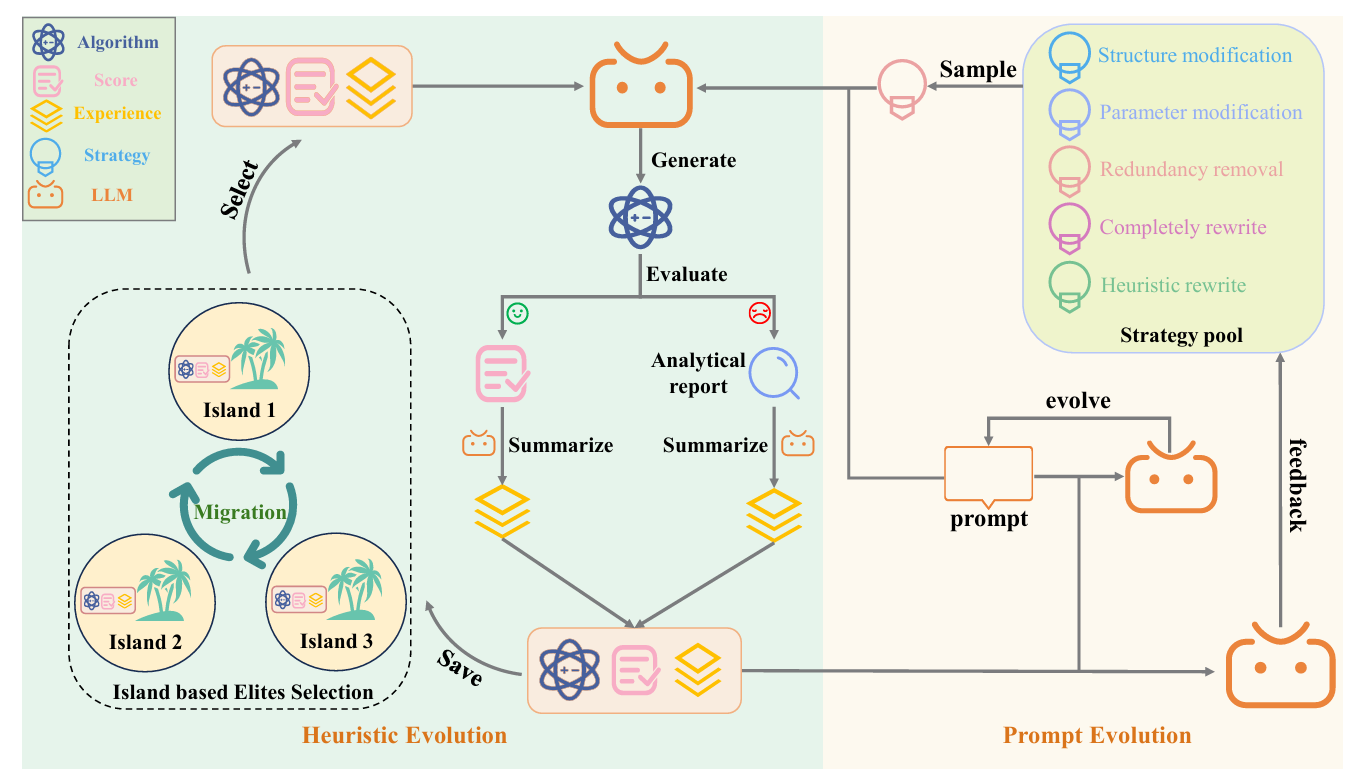
通过大语言模型(LLM)作为“智能变异算子”,EvoPH 在每一轮中:
- 生成新算法(由 LLM 根据提示词写出)
- 评估性能(运行算法并计算相对误差)
- 总结经验(记录哪些策略有效、哪些失败)
- 更新提示词(根据经验优化下一轮提示)
- 迁移精英策略(多个“岛屿”之间交换优秀算法)
审稿人评价
- 方法不新颖
- 代码是AI写的
- 很多细节没有报告,方法表述不清晰
HiFo-Prompt: Prompting with Hindsight and Foresight for LLM-based Automatic Heuristic Design
https://openreview.net/forum?id=imSLzfZ6av&utm_source=chatgpt.com
rating:26446, Accept
贡献
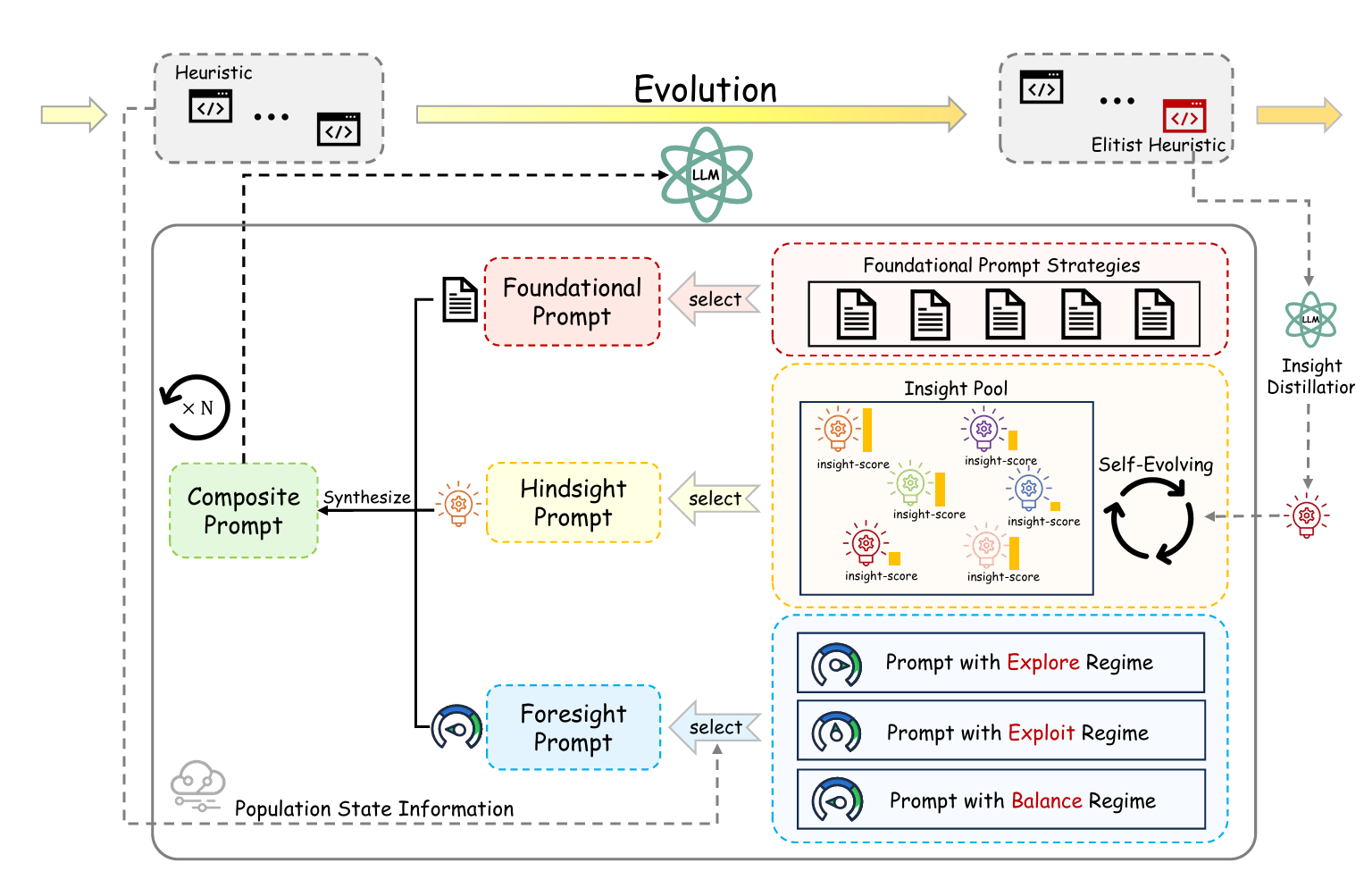
- 提出HiFo-Prompt框架
该框架引入了两个关键模块:
- Foresight(前瞻)模块:作为一个元控制器,监控种群动态(如停滞和多样性下降),主动在探索与利用之间切换搜索策略。
- Hindsight(后见)模块:构建一个持续更新的知识库(Insight Pool),从过去的高性能启发式中提炼出可复用的设计原则。
- Insight Pool(知识池)机制 使用LLM从优秀个体中提取抽象的设计原则,并通过信用分配机制(credit assignment)动态更新每个原则的“可信度”。这些原则以自然语言形式存在,能被直接嵌入提示中,指导后续生成。
- Evolutionary Navigator(进化导航器) 基于种群表现(如是否停滞、是否多样性下降)动态选择进化策略(探索、利用或平衡),并将该策略转化为自然语言指令注入提示,实现对LLM生成过程的高层次控制。
- 实验验证
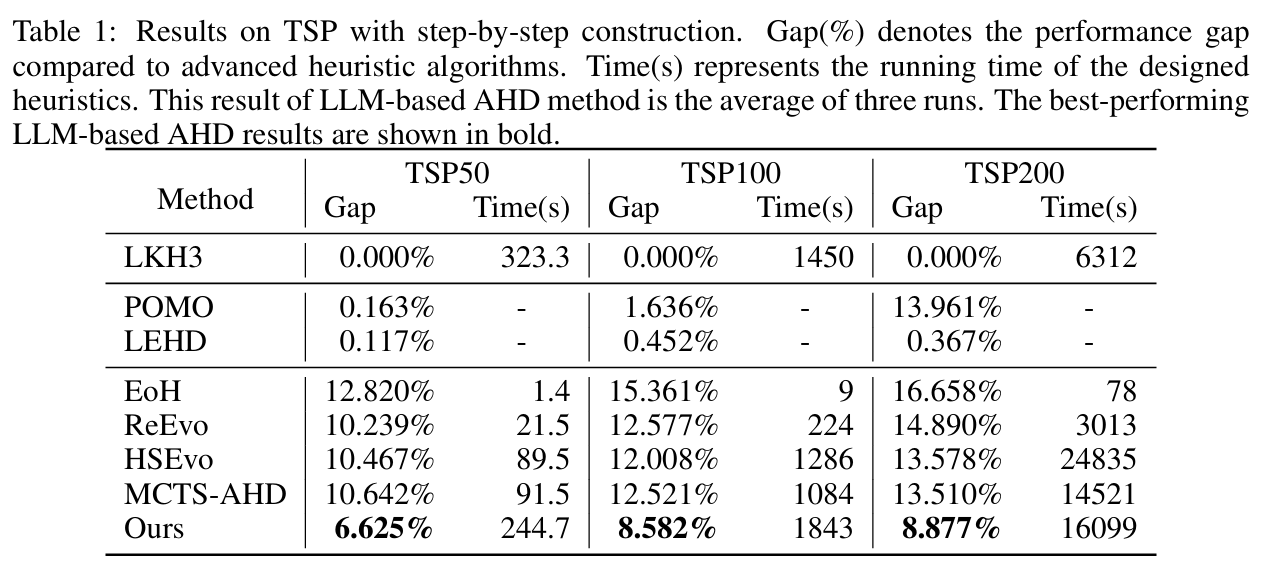
在多个经典组合优化问题上(如TSP、在线装箱、流水车间调度、贝叶斯优化)进行了广泛实验,结果表明:
- HiFo-Prompt显著优于现有的AHD方法(如EoH、ReEvo、MCTS-AHD等)。
- 在收敛速度和样本效率方面表现优异,通常只需约200次LLM调用即可发现高质量启发式。
- 在多个任务上甚至超过了人工设计的高级启发式算法(如LKH3、NEH等)。
- 消融实验与可解释性分析 论文还提供了详细的消融实验,验证了Insight Pool和Evolutionary Navigator各自对性能的关键作用,并展示了框架在不同LLM、不同参数设置下的鲁棒性。
实验

审稿人评价
反思、知识库、精炼等概念都是已有概念,并非新颖工作。
AutoMOAE: Multi-Objective Auto-Algorithm Evolution
https://openreview.net/forum?id=G8tP1Z9dLy
rating:42424,withdraw
西电的课题组
动机
解决多目标问题。
方法
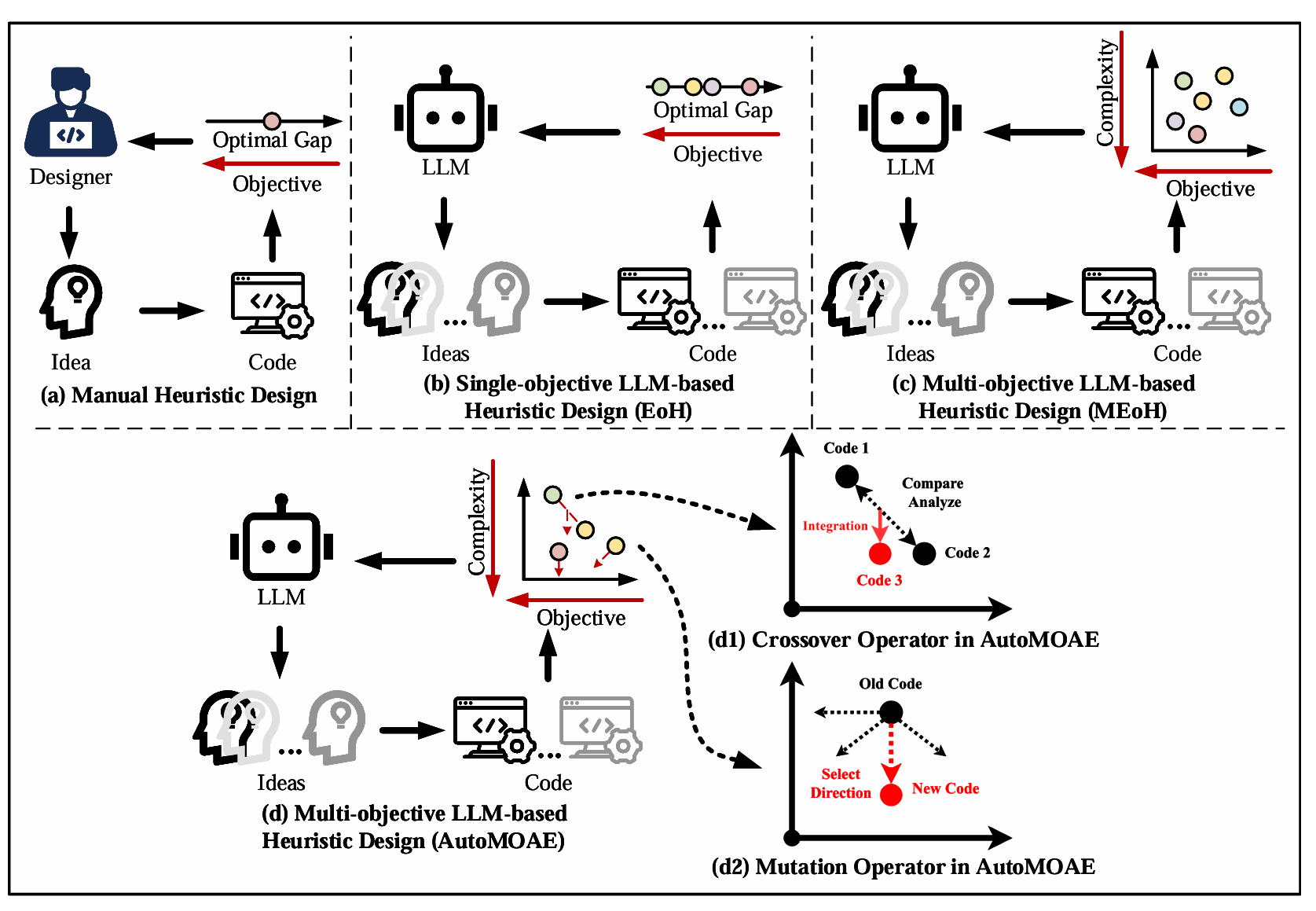
AutoMOAE 将每一个候选算法表示为一段代码片段(个体),并通过“初始化 → 遗传变异(交叉 & 突变)→ 基于 Pareto 的种群维护”这一迭代过程对种群进行精炼。
实验
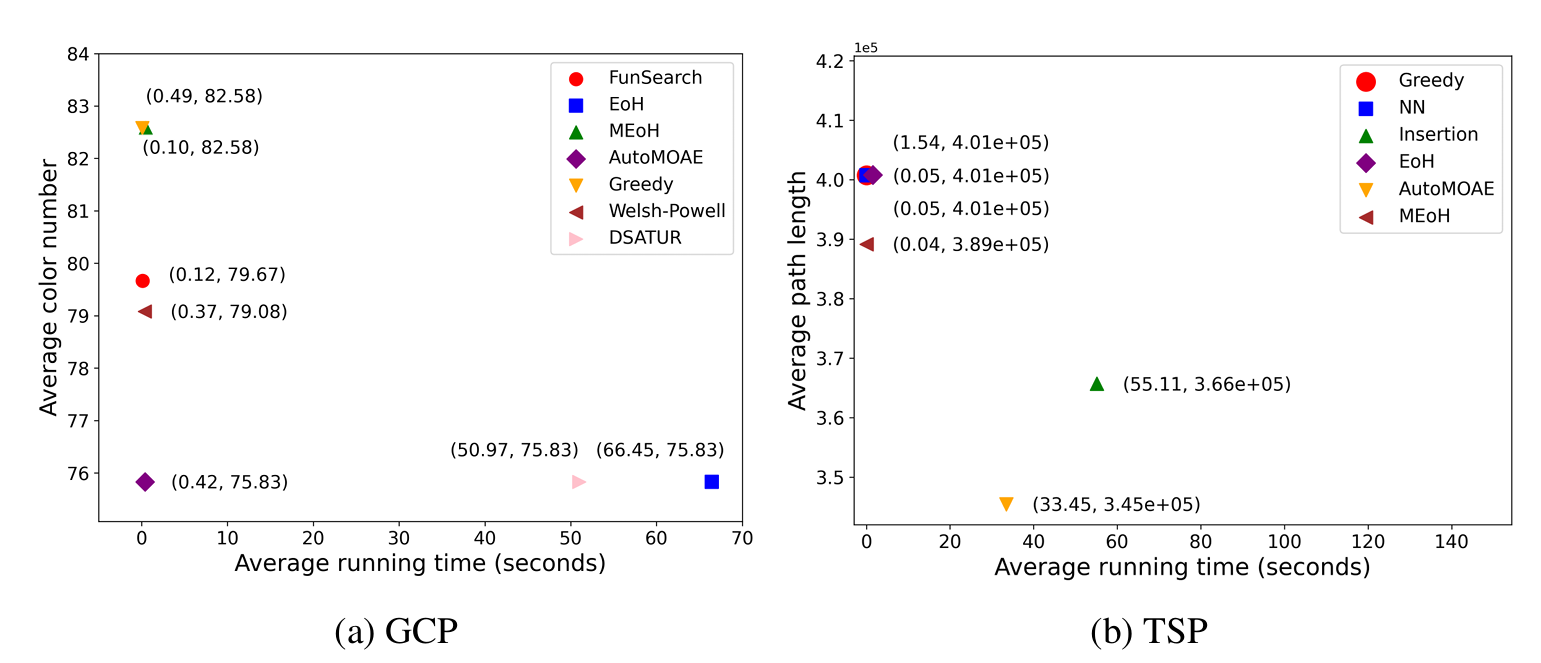
审稿人评价
贡献没讲,和原有方法的对比也没讲,实验也没怎么做,定义也不清晰。
RedAHD: Toward End-to-End LLM-Based Automatic Heuristic Design using Reductions
https://openreview.net/forum?id=6f8qlK7wN4
rating:448, Reject
痛点
- 传统做法:人工为每个 COP 设计启发式,或在预定的GAF(通用算法框架,如蚁群算法)里让 LLM 只填一个子模块(如 ACO 的启发式矩阵)。
- 痛点:仍离不开领域知识、手工实现 GAF,且不同问题要重写整套代码,远非“端到端”。
贡献
- 提出了一种全新的通用框架——基于归约的自动启发式设计(RedAHD),使现有的 LLM-EPS 方法无需依赖 GAF 即可独立运行。RedAHD 基于“归约”这一算法设计中简洁而强大的思想:将待求解的 COP 转换成更易理解的相似 COP,然后利用基于 LLM 的启发式设计方法直接为变换后的问题设计有效启发式,再间接解决原问题。该过程由 LLM 自动完成,无需人工干预。
- 在 RedAHD 中内置了一种机制:当搜索过程陷入停滞、似乎收敛到局部最优(在 COP 目标函数定义的景观内)时,自动对归约函数(负责映射两个 COP 的实例与解)进行精炼。该扩展使 RedAHD 即使面对 LLM 初始归约不够理想的情况,也能保持良好的优化性能。
省流
给定问题 A,LLM 即兴生成 M 个“听起来能高效求解、又跟 A 有点像”的候选问题 B₁…Bₘ(自然语言描述,几行字)。再即兴生成一对 Python 函数
- f:把 A 的实例 → B 的实例
- g:把 B 的解 → A 的解
方法

RedAHD 仅以待求解 COP 的规格说明作为输入,几乎无需人工干预即可输出式 (2) 定义的 $h^*$。 它维护 $N$ 个由 LLM 生成的启发式集合 $\bar P=\lbrace \bar h_1’,\ldots,\bar h_N’\rbrace $,采用某一 LLM-EPS 方法迭代寻找在有限实例集上目标值更优的启发式。 每个启发式 $h_i’\in P$ 关联一个语言归约 $r_j\in R=\lbrace r_1,\ldots,r_M\rbrace $,后者将原问题 $A$ 变换为另一 COP $B_j$。 当搜索过程停滞时,LR 会被自动精炼,避免早熟收敛。 整体包含三步: (i) 归约初始化; (ii) 多问题 LLM-EPS; (iii) 归约精炼。
归约初始化
LR 表示 一个语言归约包含以下组件:
- 用几句话自然语言描述问题 $B$。
- 根据 $A$ 与 $B$ 的描述,实现一对映射函数 $(f,g)$ 的代码片段,需遵循预定义的“归约模板”,以便与现有 LLM-EPS 方法无缝衔接。
- 基于已实现的 $(f,g)$,为所采用的 LLM-EPS 方法生成对应的“代码模板”。
- 每个 LR 被赋予一个分数,用于选择及停滞跟踪。
候选 LR 生成 给定 $A$ 的描述,RedAHD 首先提示 LLM 给出 $M_{\rm init}\ge M$ 个候选 COP $\lbrace B_j\rbrace _{j=1}^{M_{\rm init}}$ 的简短描述。 对每一个 $B_j$,RedAHD 通过一次 LLM 调用生成 $(f_j,g_j)$;再调用一次 LLM 生成与 $B_j$ 对应的代码模板。 两次调用分开进行,以减少幻觉。
启发式初始化 对每个 $B_j$,用其描述与代码模板提示 LLM,生成初始启发式集合 $P_j$。 启发式 $h_i^{(j)}$ 的优化性能(适应度)计算如下:
\[Q(h_i^{(j)}) = \frac 1 D \sum_{k=1}^D q(x^{(k)},y^{(k)}),\]其中 $q$ 为 $A$ 的目标函数(例如 TSP 取负 tour 长度),且
\[y^{(k)} = g_j\!\bigl(h_i^{(j)}(f_j(x^{(k)}))\bigr).\]重复 $\lceil N/M \rceil$ 次,得到 $P_j=\lbrace h_1^{(j)},\ldots,h_{\lceil N/M\rceil}^{(j)}\rbrace $。
选择 定义 LR 分数 $s_j$ 为其关联的前 $l$ 个最优启发式的平均适应度。 评估完 $M_{\rm init}$ 个候选 LR 后,保留分数最高的 $M$ 个。 初始启发式集合即为 $P=\bigcup_{j=1}^M P_j$,总数至少 $N$ 个。 注意:只要经 $(f_j,g_j)$ 返回的解 $y^{(k)}$ 对所有实例 $x^{(k)}$ 均合法(如 TSP 中每个节点仅访问一次),就认为 $r_j$ 有效,而不显式检查 $(f_j,g_j)$ 的正确性。
多问题 LLM-EPS
初始化完 LR 集合 $R$ 与启发式集合 $P$ 后,RedAHD 的演化流程与现有 LLM-EPS 方法一致,通常包括: (i) 从 $P$ 中选择父代启发式(随机或基于 $Q$); (ii) 通过 LLM 提示对这些启发式施加变异算子,在 $H’$ 中搜索新启发式; (iii) 控制 $\mid P\mid \le N$,仅保留最优者。
由于现在存在多个 $H’$(对应不同 $B_j$),需要高效探索扩展后的启发式空间而不增加额外开销。 因此,我们将 LLM-EPS 扩展到“多问题”场景:种群中的任意启发式,无论原本用于哪个 COP,均可无差别地作为父代,为任一 $B_j$ 生成子代。 即,为 $B_j$ 设计的启发式 $h_i^{(j)}$ 可作为算法参考,为另一 $B_{j’}$($j’\ne j$) 生成子代启发式。
相比单独为每个 $B_j$ 设计启发式,该策略有两方面优势:
- 防止某个 LR 性能过强导致种群中所有启发式都针对单一 COP,从而使其他 COP 的启发式搜索失效;
- 促进跨问题知识迁移,有助于发现未探索的启发式空间,可能带来性能提升。图 3 给出了 TSP 启发式设计中的一个支持性示例。
LR 配额 在 EoH 的每一代,每个变异算子(交叉、变异)各应用 $N$ 次,共生成 $N$ 个新启发式。 在多问题设置中,每个算子只为 $\lbrace B_j\rbrace _{j=1}^M$ 中的部分问题生成子代,且满足 $0<N_j<N$,$\sum_{j=1}^M N_j=N$。 具体配额由以下方式确定:
LR 选择 从 $R$ 中有放回采样 $N$ 次,选择概率为
- 若 $q(x,y)<0$(如 TSP):$p_j\propto 1/\mid s_j\mid $
- 若 $q(x,y)\ge 0$(如背包):$p_j\propto s_j$
该概率与 EoH 中选择父代启发式的方式类似。因此,表现更好的 LR 更可能获得较大的 $N_j$。
归约精炼
演化过程中,某一 LR 可能远优于其他 LR,从而占据几乎所有配额,导致种群几乎全为针对单一 $B_j$ 的启发式。 此时搜索退化为普通 LLM-EPS,易早熟收敛到局部最优。
为避免此现象,RedAHD 在 LR 分数停滞时自动精炼归约: 对每一个 $r_j$,若 $s_j$ 连续 $T$ 代(或评价次数)无提升,则通过 LLM 重新生成 $(f_j,g_j)$ 及对应的代码模板。 提示词同时包含 $A$ 与 $B_j$ 的描述以及当前版本。 更新后,重新计算与该 LR 关联的所有启发式适应度,进而更新 $s_j$。 仅当 $s_j$ 提升时才保留此次更新。附录 D.1 给出具体提示。
例子
TSP问题规约成:对每个节点都跑一次“最近邻”启发式,然后挑长度最短的那条回路作为近似解。
对应规约问题的启发式是:
- 先随机抽 10 个不同起点跑最近邻;
- 对每条回路再做 2-opt 局部爬坡;
- 返回最好的一条。
实验
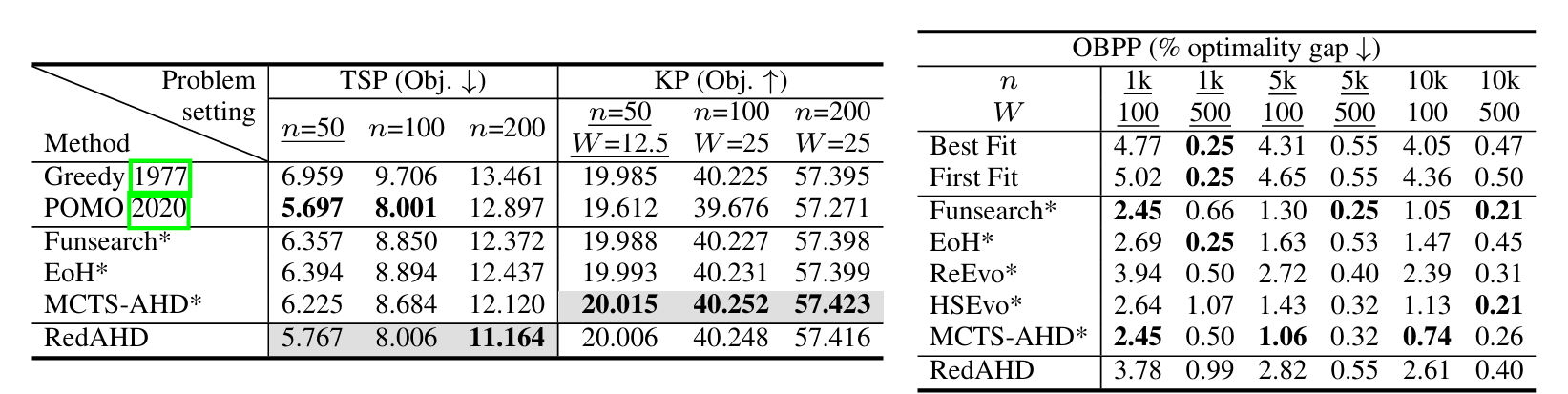

审稿人意见
都是基于实验的问题,方法本身挺有意思的。
QUBE: Enhancing Automatic Heuristic Design via Quality-Uncertainty Balanced Evolution
https://openreview.net/forum?id=y8Ctbiriia
rating:2222,withdraw
浙江大学、西湖大学
痛点
近期结合大语言模型(LLM)与进化算法(EA)的方法(如FunSearch)虽取得进展,但在探索(exploration)与利用(exploitation)的平衡上存在不足,导致性能受限。
贡献
- 提出QUBE框架
- 关键创新:引入质量-不确定性权衡准则(QUTC),基于新提出的不确定性融合质量(UIQ)指标评估候选启发式。
- 动态平衡:通过UCB(上置信界)思想,同时考虑候选解的历史表现(质量)和未被充分探索的潜力(不确定性),动态调整搜索策略。
- 算法设计
- 父代选择:在进化过程中,优先选择UIQ值高的候选解作为父代,兼顾高潜力与低探索区域。
- 岛屿重置机制:定期淘汰低UIQ的岛屿(种群),避免资源浪费在低潜力区域。
个人见解
QUTC有点像蒙特卡洛的评估方式。
方法
质量-不确定性权衡准则(QUTC)
1) 聚类质量定义
与静态地使用样本自身得分不同,我们定义聚类$\mathbb{C}$的演化质量为:
\[Q_t(\mathbb{C}) = \frac{1}{\sum_{c\in\mathbb{C}}\mid \mathcal{P}_{c,t}\mid } \sum_{c\in\mathbb{C}}\sum_{a\in\mathcal{P}_{c,t}} s(a)\]其中$\mathcal{P}_{c,t}$表示截至时刻$t$以$c$为父代生成的所有子代集合。$Q_t(\mathbb{C})$动态估计“以$\mathbb{C}$为父代能产生多好的后代”,直接关联利用价值。
2) 不确定性融合质量(UIQ)
受UCB启发,引入访问次数$N_t(\mathbb{C})$(截至$t$聚类$\mathbb{C}$被用作父代的总次数)与超参数$k$,定义
\[\tilde{Q}_t(\mathbb{C}) = Q_t(\mathbb{C}) + k \sqrt{\frac{\ln t}{N_t(\mathbb{C})}}\]UIQ同时反映:
- 利用项 $Q_t(\mathbb{C})$:历史后代表现越好,值越高;
- 探索项 $k\sqrt{\frac{\ln t}{N_t(\mathbb{C})}}$:访问越少,不确定性越高,奖励越大。
QUTC按 $\tilde{Q}_t(\mathbb{C})$ 对所有聚类排序,实现探索与利用的自适应平衡。
实验
结果太粗糙了,几乎没怎么做实验。
###
HeuriGym: An Agentic Benchmark for LLM-Crafted Heuristics in Combinatorial Optimization
https://openreview.net/forum?id=HWxHUO15Yy
rating:6864, Accept
康奈尔大学、哈佛大学、Nvidia
痛点
尽管大语言模型在推理和代码生成方面取得了显著进展,但现有评估方法存在以下问题:
- 封闭性问题饱和:如AIME、HumanEval等基准测试,模型性能已接近天花板,且容易被“背题”。
- 主观评估不稳定:如Chatbot Arena,评估标准不一致,容易受表面因素影响。
- 缺乏真实工程挑战:现有测试难以反映LLM在真实科研与工程问题中的能力。
贡献
- 新基准:HeuriGym 提供了一个开放、可扩展、具有现实意义的组合优化评估平台。
- 新指标:QYI 综合衡量解的质量与可行性,适用于迭代式智能体评估。
- 实证研究:系统评估了当前LLM在复杂工程问题上的真实能力,揭示了差距与改进方向。
框架
HeuriGym 是一个面向组合优化问题的智能体评估框架,其核心流程如下:
- 问题描述:向LLM提供明确的组合优化问题(如调度、布线、路径规划等)。
- 代码生成:LLM生成完整的启发式算法代码(Python为主)。
- 执行与验证:代码在沙箱中运行,检查是否满足约束条件。
- 反馈与迭代:将运行结果(错误、得分、超时等)反馈给LLM,支持多轮优化。
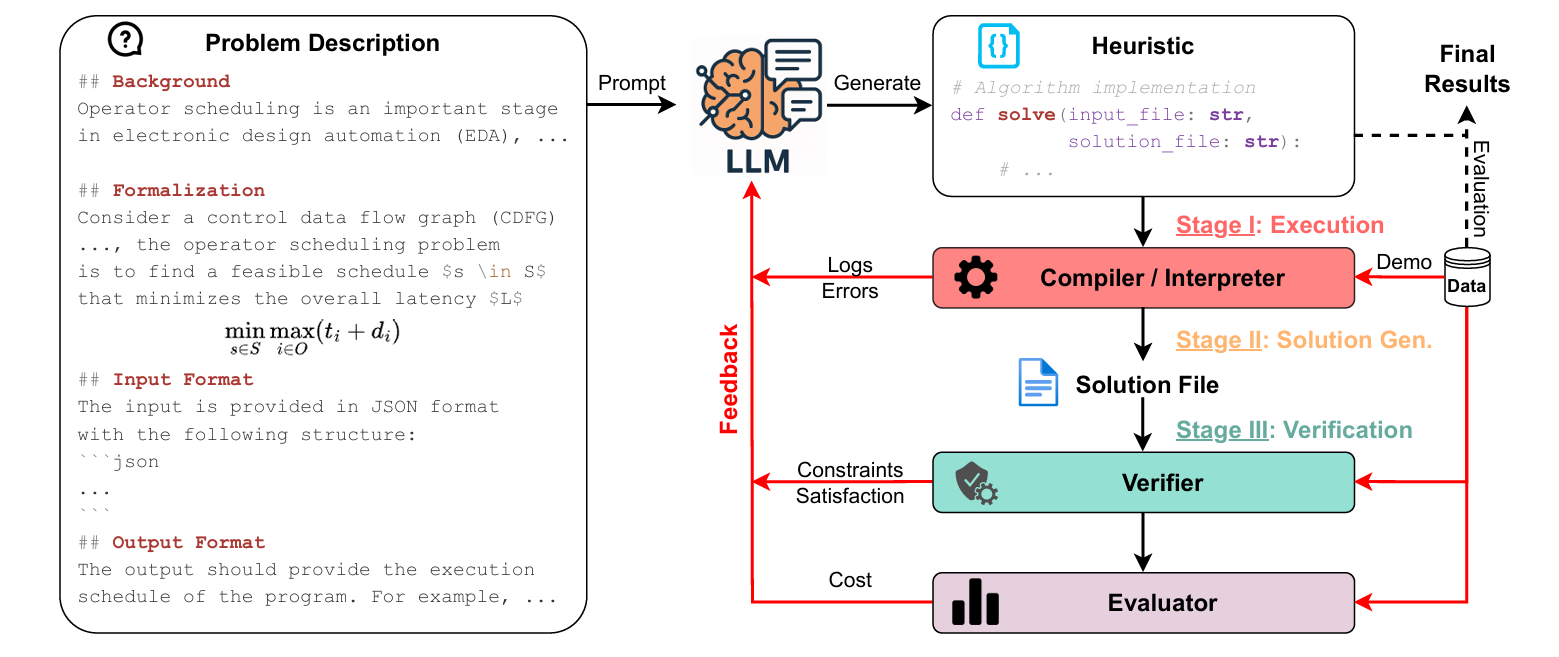
方法
问题描述
如图1左侧所示,我们以算子调度(operator scheduling)为例,这是一个电子设计自动化(EDA)中的经典优化问题。每个基准任务都配有结构化的问题描述,包含以下三部分:
- 背景(Background):介绍优化问题的背景与关键术语,帮助大语言模型理解问题设定。
- 形式化(Formalization):使用数学符号定义优化目标与约束条件(例如在硬件资源限制下最小化延迟),引导模型朝向目标导向的算法设计。
- 输入/输出格式(Input/Output Format):规定输入输出文件的结构,为解析与执行提供明确预期。
提示设计
有效的提示工程对于发挥大语言模型能力至关重要。我们为每个问题构建了系统级与用户级提示,并在附录中提供了完整示例。
- 系统提示(System Prompt):包含机器配置(如CPU核心数、内存限制)、可用库及其版本号、任务特定约束(如执行超时)。该环境说明旨在防止模型做出不切实际假设或生成低效解。
- 用户提示(User Prompt):在首次迭代中,用户提示包含问题描述与一个预定义函数签名的代码骨架。如图1所示,大语言模型仅获得函数接口——函数名、输入路径与输出路径——不包含任何数据结构或算法提示。这与已有工作(如FunSearch、AlphaEvolve)不同,后者通常手工提供部分实现或限制设计空间。在此,大语言模型必须整体性地推理:解析输入、构建内部表示、从零设计并实现启发式算法。
反馈循环
为模拟少样本上下文学习设置,我们将数据集划分为:
- 演示集(demonstration set):约5个实例,用于在迭代过程中提供基于示例的反馈;
- 评估集(evaluation set):更大规模,仅在模型稳定后用于最终性能测试。
每个问题都配有:
- 验证器(verifier):检查解是否满足问题特定约束(如算子调度中的依赖保留);
- 评估器(evaluator):根据优化目标计算解的成本。
若验证失败,诊断信息将被记录;每次迭代后,我们将生成的解、执行轨迹、验证结果与目标得分追加到提示中,供下一轮使用,从而实现模型的渐进式改进。
指标设计
传统大语言模型基准主要使用 PASS@k 指标,衡量在 top-k 样本中是否生成正确答案。虽然该指标适用于单轮、有确定真值的测试,但无法反映多轮智能体设置中所需的迭代推理与问题解决能力。
为此,我们提出新指标:
\[\mathrm{SOLVE}_{s}@\mathit{i} = \frac{1}{N}\sum_{n=1}^{N}\mathbb{1}\big(\text{pass stage } s \text{ at the } i\text{-th iteration}\big)\]其中:
- $N$:输入实例总数;
- $s \in \lbrace \mathrm{I}, \mathrm{II}, \mathrm{III}\rbrace $:表示解必须通过的管道阶段,分别代表智能体推理中的关键里程碑:
| 阶段 | 含义 |
|---|---|
| Stage I | 执行:程序必须成功编译/解释,包含所有必要库,并完成基本 I/O 操作。 |
| Stage II | 解生成:程序必须在预设超时内产生非空输出,并符合预期输出格式。 |
| Stage III | 验证:解必须通过问题特定验证器,满足所有约束条件。 |
然而,$\mathrm{SOLVE}_{s}@\mathit{i}$ 仅表明是否最终产生可行解,未考虑解的质量。为此,我们定义以下两个补充指标:
质量(QUALITY)
\[\mathbf{QUALITY} = \frac{1}{\hat{N}}\sum_{n=1}^{\hat{N}} \min\left(1, \frac{c_{n}^{\star}}{c_{n}}\right)\]- $c_n$:大语言模型生成解的目标成本;
- $c_n^{\star}$:专家解的目标成本;
- $\hat{N}$:在某轮迭代中通过验证(Stage III)的实例数。
我们使用截断版本的质量指标(上限为1),也可使用非截断版本衡量模型是否超越专家。
成功率(YIELD)
\[\mathbf{YIELD} = \frac{\hat{N}}{N}\]综合指标:QYI(Quality-Yield Index)
我们定义统一指标 QYI 为质量与成功率的调和平均(类比 F1 分数):
\[\mathrm{QYI} = \frac{(1+\beta^{2})\cdot \mathrm{QUALITY} \cdot \mathrm{YIELD}}{(\beta^{2}\cdot \mathrm{QUALITY}) + \mathrm{YIELD}}\]- 默认 $\beta = 1$,即质量与成功率权重相等;
- QYI 取值范围为 $[0, 1]$,1 表示专家级表现;
- 我们还定义了加权 QYI,按每个问题的实例数加权平均,用于总体性能评估。
结论
- LLM能设计启发式算法,但质量有限:能跑通代码,但优化效果不佳。
- 多轮反馈有效:LLM能从错误中学习并逐步改进。
- 问题理解能力参差不齐:部分模型在复杂约束下容易出错(如API误用、逻辑错误)。