ICLR 2026 review阶段,LLM AHD合集三
Cognitively Inspired Reflective Evolution: Interactive Multi-Turn LLM–EA Synthesis of Heuristics for Combinatorial Optimization
https://openreview.net/forum?id=31VTD5pS2v
rating:2224, withdraw
痛点
大型语言模型(LLMs)被尝试用于自动生成启发式代码,但大多数方法只是一次性生成(one-shot),缺乏反馈与迭代优化,导致生成的启发式算法脆弱、不可解释、难以改进。
框架
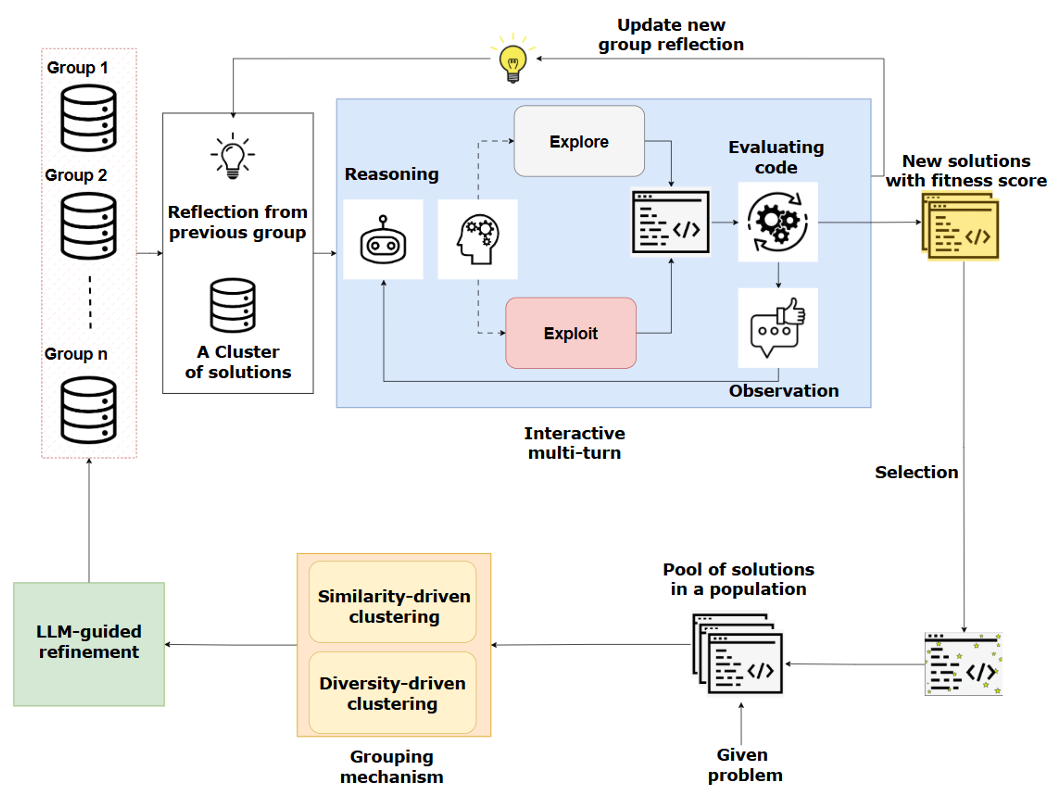
CIRE 将 LLM 视为一个可交互、多轮推理的智能体,而不是一次性代码生成器。它结合了演化算法(EA)与认知启发的反思机制,通过以下三阶段循环迭代优化启发式:
-
行为聚类(Grouping & Behavioral Clustering) 将候选启发式按性能表现与代码结构聚类,形成“行为相似”或“结构多样”的组,供LLM分析。
聚类后,包括同质组和异质组,异质组补充了多样性。
-
多轮反思优化(Reflective Multi-Turn Refinement) LLM 对每组启发式进行多轮对话式分析,识别其优劣,提出改进建议,并生成新的启发式版本。 每轮包括:
-
观察(Observe):查看当前启发式的表现;
-
推理(Reason):分析失败原因、成功因素;
-
行动(Act):决定是探索新策略(explore)还是利用现有策略(exploit)。
探索:当近期改进停滞或结构趋同,LLM 提出全新算子或跨簇重组,以扩大搜索前沿。
利用:当发现高质量候选,LLM 进行参数微调、结构打磨,系统性地提升性能。
-
-
演化控制(EA Meta-Controller) 一个演化控制器负责选择、验证、保留最有潜力的启发式,维持多样性与性能的平衡。
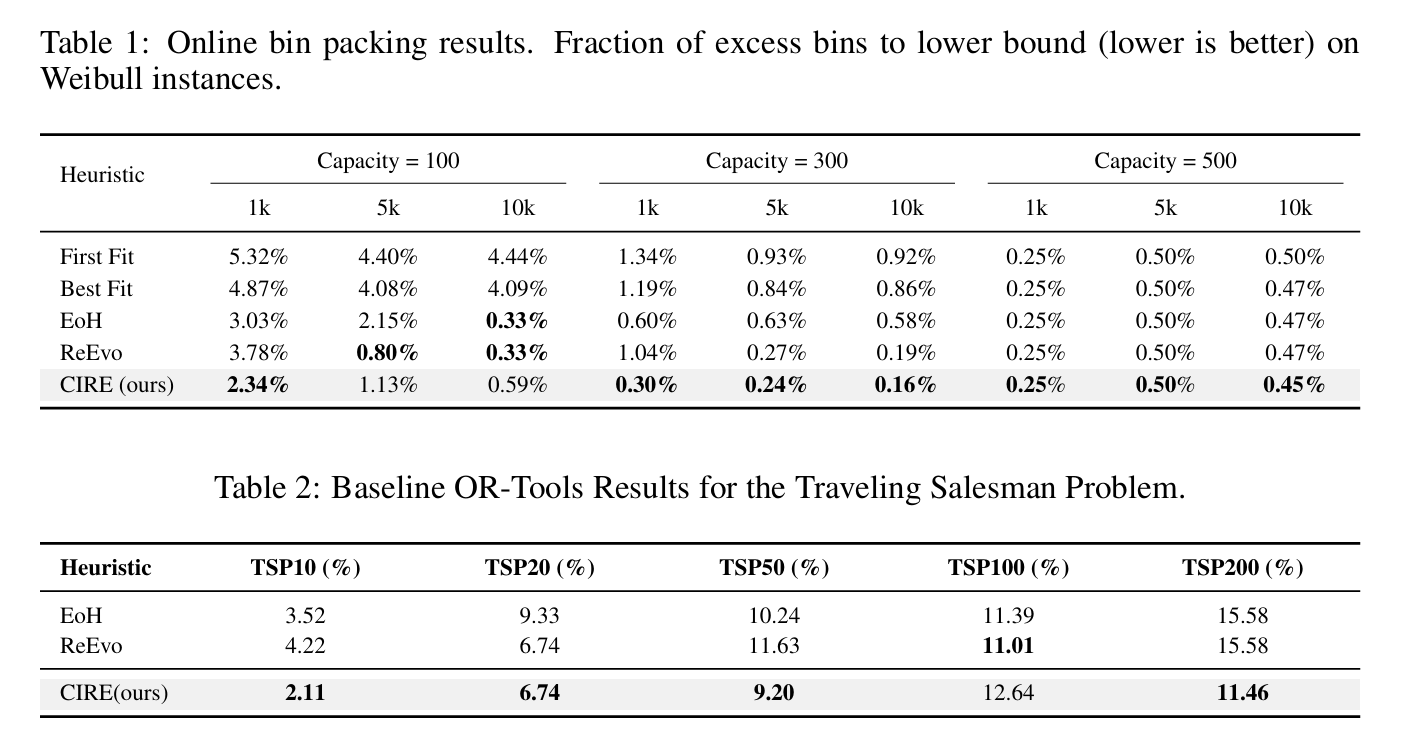
实验
审稿人意见
实验太少没有说服力,细节不充分,没有消融实验。
Automating Thought of Search: A Journey Towards Soundness and Completeness
https://openreview.net/forum?id=DE9Vapk5DW
康奈尔大学、IBM
rating:44244,withdraw(投过NIPS2024)
背景
近年来,大语言模型(LLMs)被广泛用于解决规划问题,尤其是通过搜索方式。然而,大多数方法将 LLM 作为“世界模型”来生成状态转移,牺牲了正确性(soundness)和完备性(completeness)以换取灵活性。
Thought of Search (ToS) 是一种新兴方法,它让 LLM 用代码定义搜索空间(即生成 succ 后继函数和 isgoal 目标判断函数),从而保证搜索的可靠性和效率。ToS 在多个基准测试中达到了 100% 准确率,但其缺点是需要人类专家参与反馈循环。
目标
提出 AutoToS,目标是去除人类在反馈循环中的参与,通过自动化的方式引导 LLM 生成正确且完备的搜索组件(succ 和 isgoal 函数),从而解决规划问题。
方法
AutoToS 的核心思想是:用单元测试(unit tests)代替人类反馈,通过自动化的测试-修复循环来迭代改进 LLM 生成的代码。
四个步骤
- 初始生成:让 LLM 生成
succ和isgoal函数的初始版本。 - 目标函数正确性检查:用已知的 goal/non-goal 状态测试
isgoal是否正确。 - 后继函数正确性检查:
- 检查是否修改了输入状态;
- 检查是否超时;
- 检查状态转移是否“合理”(如状态长度是否减1);
- 后继函数完备性检查(可选):检查是否遗漏了某些合法后继状态。
每一步失败时,都会将错误信息反馈给 LLM,要求其修复代码。
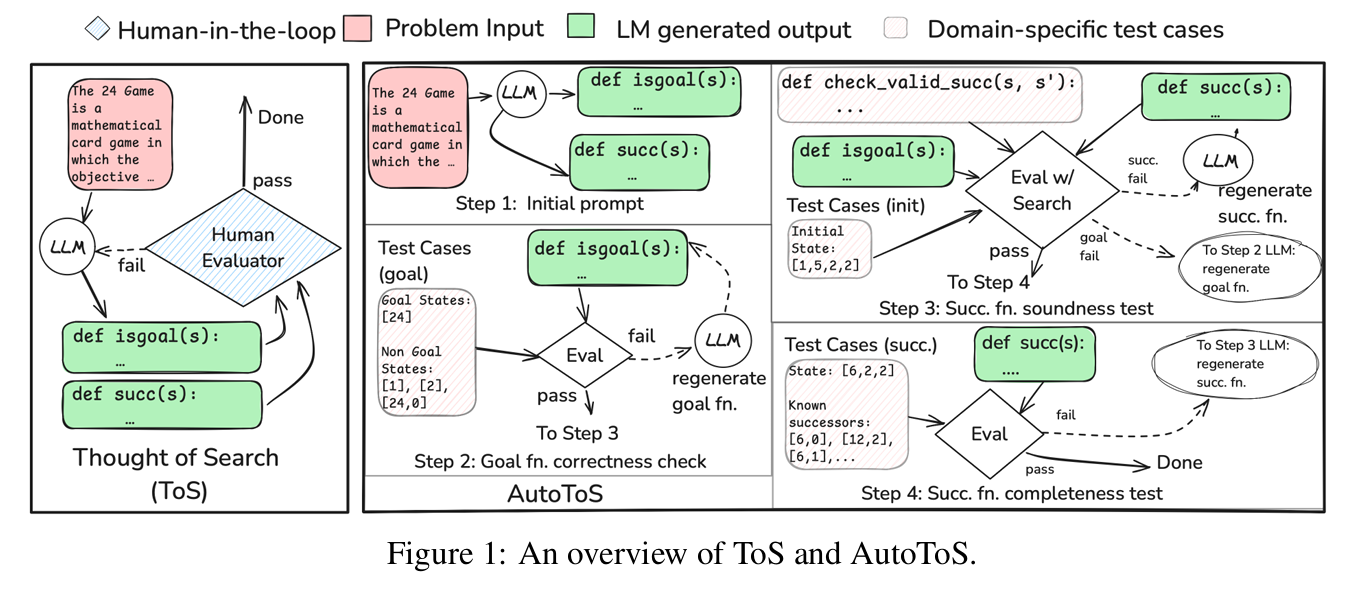
例子
24Game(二十四点)
状态表示:一个数字列表,长度 ≤ 4 目标:通过四则运算,最终得到
[24]操作:每次选两个数,做一次运算,用结果替换它们,列表长度减 1
例子 1:isgoal 出错 → 自动反馈修复
① 初始代码(LLM 第一次生成)
def isgoal(s):
return 24 in s
② 单元测试失败
- 输入:
[24, 1] - 期望输出:
False(因为还剩两个数,游戏未结束) - 实际输出:
True(函数错误地认为已达成目标)
③ 自动反馈提示(原文逐字)
The goal test function failed on the following input state
[24, 1], incorrectly reporting it as a goal state. First think step by step what it means for a state to be a goal state in this domain. Then think through in words why the goal test function incorrectly reported input state:[24, 1]as a goal state. Now, revise the goal test function and ensure it returns false for the input state. Remember how you fixed the previous mistakes, if any. Keep the same function signature.
④ 修复后的代码(LLM 返回)
def isgoal(s):
return len(s) == 1 and s[0] == 24
例子 2:succ 出错 → 局部正确性检查失败
① 初始代码(片段)
def succ(s):
# 某版本实现
...
return [[6, 5]] # 错误:长度没有减 1
② 局部正确性检查失败
- 父状态:
[1, 1, 4, 6](长度 4) - 后继状态:
[6, 5](长度 2) → 长度应减 1,但实际减 2 → 非法转移
③ 自动反馈提示
Invalid transformation: length mismatch - the length of a successor must be one less than the parent. Let’s think step by step. First think through in words why the successor function produced a successor that had a length that was not exactly one less than the parent. Then provide the complete Python code for the revised successor function that ensures the length of a successor is exactly one less than the parent. Remember how you fixed the previous mistakes, if any. Keep the same function signature.
④ 修复后
- 确保每次只合并两个数,其余数保留 → 长度严格减 1
例子 3:succ 缺后继 → 完备性检查失败
① 父状态
[1, 1, 4, 6]
② 已知合法后继(部分)
[1, 4, 7], [-5, 1, 4], [1, 1, 2], [1, 5, 6], [0.25, 1, 6], ...
③ LLM 生成版本漏掉了上述后继
④ 自动反馈提示
Successor function when run on the state
[1, 1, 4, 6]failed to produce all successors. Missing successors are:[[1, 4, 7], [-5, 1, 4], [1, 1, 2], [1, 5, 6], [0.25, 1, 6], ...]First think step by step why the successor function failed to produce all successors of the state. Then, fix the successor function. Remember how you fixed the previous mistakes, if any. Keep the same function signature.
⑤ 修复后
- LLM 补全了所有可能的二元运算组合,确保完备性
实验
测试了5个代表性搜索/规划问题
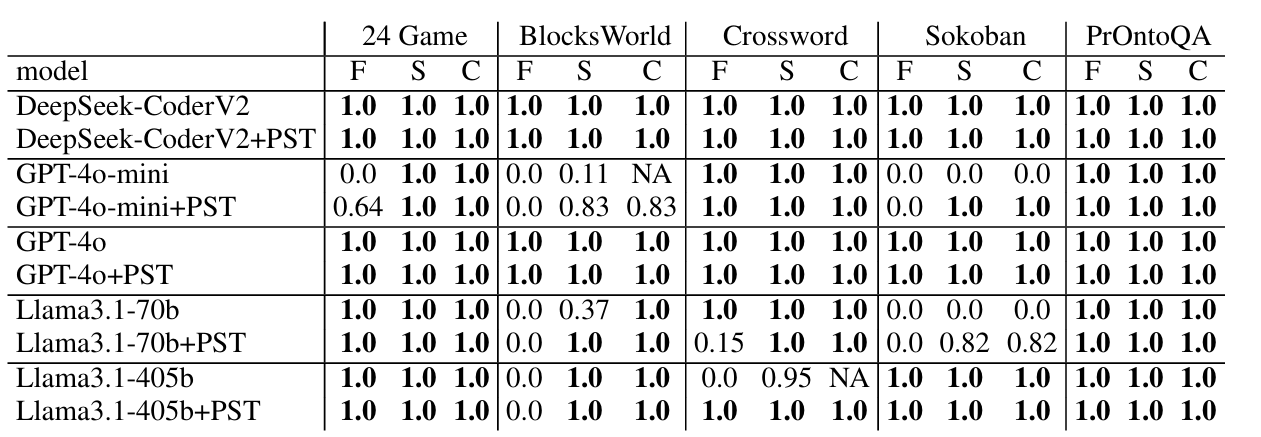
- 所有模型在所有领域都达到了 100% 准确率(至少在一次试验中)
- 所需的 LLM 调用次数与 ToS 有人类参与时相当
- 引入“部分正确性检查”(PST)显著提升了准确
- 较小的模型(如 GPT-4o-mini)也能表现良好
审稿人意见
并未消除人类影响,还是需要人工校验。贡献比较简单,实验结果也略微夸大。
Building Learning Context For Autonomous Agents Through Generative Optimization
https://openreview.net/forum?id=wtLyksjIdl
Google DeepMind、斯坦福、CMU、微软等
rating:2442,withdraw
痛点
- 当前 LLM 智能体依赖人工设计提示、规则、工作流,难以自动适应复杂任务。
- 生成式优化(Generative Optimization)用 LLM 作为优化器,通过反馈迭代改进代码/提示,但存在:
- 行为不稳定
- 目标不对齐(misalignment)
- 学习上下文缺失 → 导致“学不对”或“学不会”
贡献
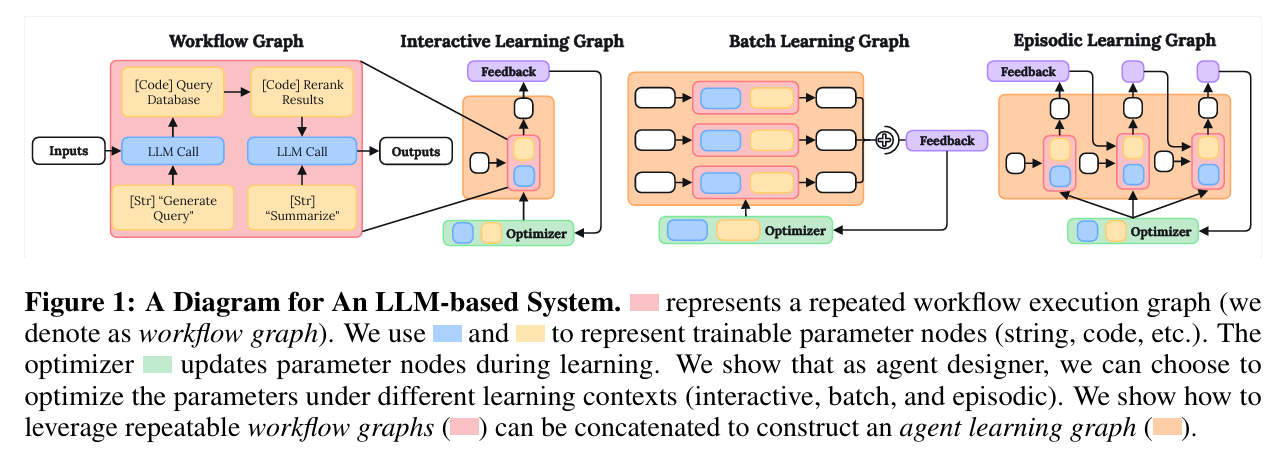
- 提出“学习上下文”(Learning Context)概念
- 指出:仅定义工作流(workflow)不足以让智能体学习,必须构建“学习图”(Learning Graph)。
- 引入三种模板,将工作流嵌入不同学习上下文:
| 模板类型 | 适用场景 | 特点 |
|---|---|---|
| Interactive | 在线学习、实时反馈 | 每步更新参数 |
| Batch | 监督/偏好学习 | 小批量样本聚合反馈 |
| Episodic | 强化学习、长期决策 | 整轮结束后更新 |
- 构建“元图”(Meta-Graph)机制
- 用运算符
⊕(batchify)与⇒(因果链)将工作流组合成“学习图”,明确:- 何时更新参数
- 如何利用反馈
- 如何捕捉时序依赖
- 三大任务验证:首次实现“用 LLM 优化器学会玩 Atari”
| 任务 | 成果 | 亮点 |
|---|---|---|
| Atari 游戏 | 在 Pong、Breakout、Space Invaders 上 媲美 DQN/PPO,训练时间减少 50–90% | 仅通过 Python 代码 学习策略,不更新神经网络权重 |
| 数据科学(MLAgentBench) | 自动构建 ML 管道,Kaggle 排行榜超越 86.6% 人类选手 | 学会特征工程、模型集成、超参调优 |
| 语言理解(BBEH/GSM8K) | GSM8K 准确率从 78.9% → 93.4% | 学会提示工程与答案提取策略 |
方法
看不懂,总体来说是希望将LLM的求解变成一个计算图。
审稿人意见
写作混乱,方法中有很多手工设计场景,感觉是个很工程的场景。
Evolution Strategies at Scale: LLM Fine-Tuning Beyond Reinforcement Learning
https://openreview.net/forum?id=1zqmmcjvdN
Cognizant AI Lab、MIT
rating:424, withdraw
(做的LLM微调,传统是用RL微调,有一种是进化算法来微调,但LLM参数很大,无法直接应用,因此本文改进了进化算法成功微调LLM)
背景
预训练大语言模型(LLMs)在下游任务上的微调是 AI 部署流程中的关键步骤。强化学习(RL)无疑是目前最主流的微调方法,催生了许多最先进的 LLM。相比之下,进化策略(Evolution Strategies, ES)曾在仅含数百万参数的模型上与 RL 表现相当,却因“难以扩展到大模型”的悲观看法而被忽视。
痛点
RL 微调的挑战
- 样本效率低:RL 在处理仅含结果奖励(outcome-only reward)的长周期任务时,梯度估计方差大,信用分配困难。
- 对基础模型敏感:不同模型上表现不一致。
- 易 reward hacking:RL 倾向于“破解”奖励函数,产生不符合预期的行为。
- 训练不稳定:相同超参下多次运行结果差异大,增加调参成本。
ES 的优势与瓶颈
- 高度并行
- 对长周期奖励鲁棒
- 无需反向传播,节省显存
- 对超参不敏感
然而,ES 直接优化参数空间的做法在过去仅限于百万级参数的模型。LLM 参数量达数十亿,使得“在参数空间中搜索”被认为不可行。
贡献
- 首次成功将 ES 扩展到直接微调 LLM 的全部参数,并在多个方面优于现有 RL 微调方法,包括:
- 样本效率更高
- 对长周期奖励更鲁棒
- 对不同基础模型更稳定
- 不易出现 reward hacking
- 多次运行结果更一致
因此,ES 为 LLM 微调开辟了一条超越当前 RL 技术的新方向。
-
首次实现:在数十亿参数空间中直接搜索,仅用种群大小 $N=30$,即可高效微调 LLM。
-
关键算法简化
原始 ES 更新公式为:
\[\theta_t \leftarrow \theta_{t-1} + \frac{\alpha}{\sigma} \cdot \frac{1}{N} \sum_{n=1}^{N} R_n \varepsilon_n\]本文将其简化为:
\[\theta_t \leftarrow \theta_{t-1} + \alpha \cdot \frac{1}{N} \sum_{n=1}^{N} R_n \varepsilon_n\]即将 $\frac{1}{\sigma}$ 吸收进学习率 $\alpha$,简化计算与调参。
方法
基础 ES 算法
自然进化策略(Natural Evolution Strategies, NES) 的算法简化版,整体设计与 OpenAI ES 类似:固定协方差的高斯扰动。
给定预训练 LLM 的初始参数 $\theta_0$ 与奖励函数 $R(\cdot)$,目标是通过微调参数使奖励最大化。算法流程如下:
Require: 预训练 LLM 初始参数 θ₀,奖励函数 R(·),总迭代次数 T,种群大小 N,噪声尺度 σ,学习率 α
for t = 1 to T do
for n = 1 to N do
采样噪声 εₙ ∼ N(0, I)
计算扰动后奖励 Rₙ = R(θ_{t-1} + σ · εₙ)
end for
对 {Rₙ} 做 z-score 标准化
更新参数 θ_t ← θ_{t-1} + α · (1/N) Σ_{n=1}^{N} Rₙ εₙ
end for
注:原文标准更新式含系数 $1/\sigma$,本文将其吸收进学习率 α,从而简化实现与调参。
面向 LLM 微调的实现细节
(1) 基于随机种子的噪声复用(Noise retrieval with random seeds)
- 不保存高维噪声 $\varepsilon$,仅保存随机种子 $s_n$
- 需要时重新设置 RNG 状态即可精确复现 $\varepsilon$
- 显存占用从 $\mathcal{O}(N \cdot \mid \theta\mid )$ 降至 $\mathcal{O}(N)$
(2) 并行评估(Parallel evaluations)
- 每轮 $N$ 个扰动模型完全并行推理
- 每个进程分配一个种子 $s_n$,独立计算 $R_n$
- 通信仅传输标量奖励,带宽开销极小
(3) 逐层原地扰动与恢复(Layer-level in-place perturbation & restoration)
- 按层(layer)遍历参数:
- 采样该层噪声 $\varepsilon_{n,l} \sim \mathcal{N}(0, \mathbf{I})$
- 原地扰动:$\theta_l \leftarrow \theta_l + \sigma \cdot \varepsilon_{n,l}$
- 前向推理得 $R_n$
- 原地恢复:$\theta_l \leftarrow \theta_l - \sigma \cdot \varepsilon_{n,l}$
- 峰值显存仅增加一层大小,与总参数量无关
(4) 奖励标准化(Reward normalization)
-
每轮对所有 $R_n$ 做 z-score:
\[Z_n = \frac{R_n - \mu_R}{\sigma_R}\] -
保证不同任务、不同迭代之间的奖励尺度一致,无需手动 rescale
(5) 贪婪解码(Greedy decoding)
- 扰动模型生成回答时不使用采样,而是 greedy decode
- 消除动作空间随机性,所有性能差异仅来源于参数扰动,便于分析
(6) 参数更新的分块累加(Decomposed parameter update)
-
主进程逐层、逐种子地原地累加更新:
\[\theta_l \leftarrow \theta_l + \frac{\alpha}{N} \sum_{n=1}^{N} Z_n \cdot \varepsilon_{n,l}\] -
避免一次性构造全参数梯度张量,进一步降低峰值显存
(7) 学习率消化(Learning rate digestion)
- 将标准 NES 更新中的系数 $1/\sigma$ 直接吸收进 α
- 简化超参列表,只需调节 α 与 σ 的相对大小
显存与计算复杂度
| 项目 | 复杂度 | 说明 |
|---|---|---|
| 峰值显存 | $\mathcal{O}(\mid \theta_{\text{layer}}\mid )$ | 与层大小成比例,与总参数量无关 |
| 通信量 | $\mathcal{O}(N)$ | 每轮仅传输标量奖励 |
| 计算 | 可线性扩展 | 每轮 $N$ 次前向推理可完全并行 |
与现有 ES 实现的差异
| 技术点 | 本文实现 | OpenAI ES 等早期工作 |
|---|---|---|
| 种群大小 $N$ | 30 即可 | 需 10 000+ |
| 模型规模 | 数十亿参数 | 百万级 |
| 显存优化 | 逐层扰动 | 全参数复制 |
| 奖励变换 | 仅用 z-score | rank-Fitness、VBN 等复杂技巧 |
| 优化器 | 无( vanilla ES ) | Adam、权重衰减等 |
本文未使用 mirrored sampling、rank transformation、weight decay、Adam 等常见技巧,以纯粹 vanilla ES 展现其在大模型上的潜力。
审稿意见
方法的能力有点夸大,实验任务太少没有泛用性。
ENCOURAGING CRITICAL THINKING FOR MULTIAGENT DEBATE
https://openreview.net/forum?id=owpU8gxnkM
rating:4226, Reject
痛点
传统多轮自我反思或单一策略提示(如CoT、Self-Reflection)在多次迭代后容易出现收益递减,因为模型倾向于重复相似的推理路径,缺乏多样性与纠错能力。
贡献
- 策略生成器(Strategy Generator)
- 不再使用固定模板(如CoT、Step-Back),而是让模型自动生成多样化的推理策略。
- 每个策略分配给一个独立智能体,形成策略条件生成(strategy-conditioned generation)。
- 多智能体辩论机制
- 多个智能体基于不同策略生成初始解。
- 通过多轮辩论互相 critique,逐步修正推理路径。
- 最终通过多数投票构造伪标签(pseudo-label),无需人工标注。
- 质量+多样性双轮筛选
- 正确性筛选:只保留与伪标签一致的解。
- 多样性筛选:使用高斯核函数(RBF kernel)度量解之间的语义相似度,剔除冗余路径,保留推理多样性。
- 策略对齐:若最终解偏离初始策略,自动重构策略以匹配成功路径。
- 迭代微调策略生成器
- 用筛选后的(问题, 策略)对微调策略生成器,形成自我强化闭环。
- 实验表明,仅需1轮微调即可显著超越8个强基线,多轮后持续提升。
方法
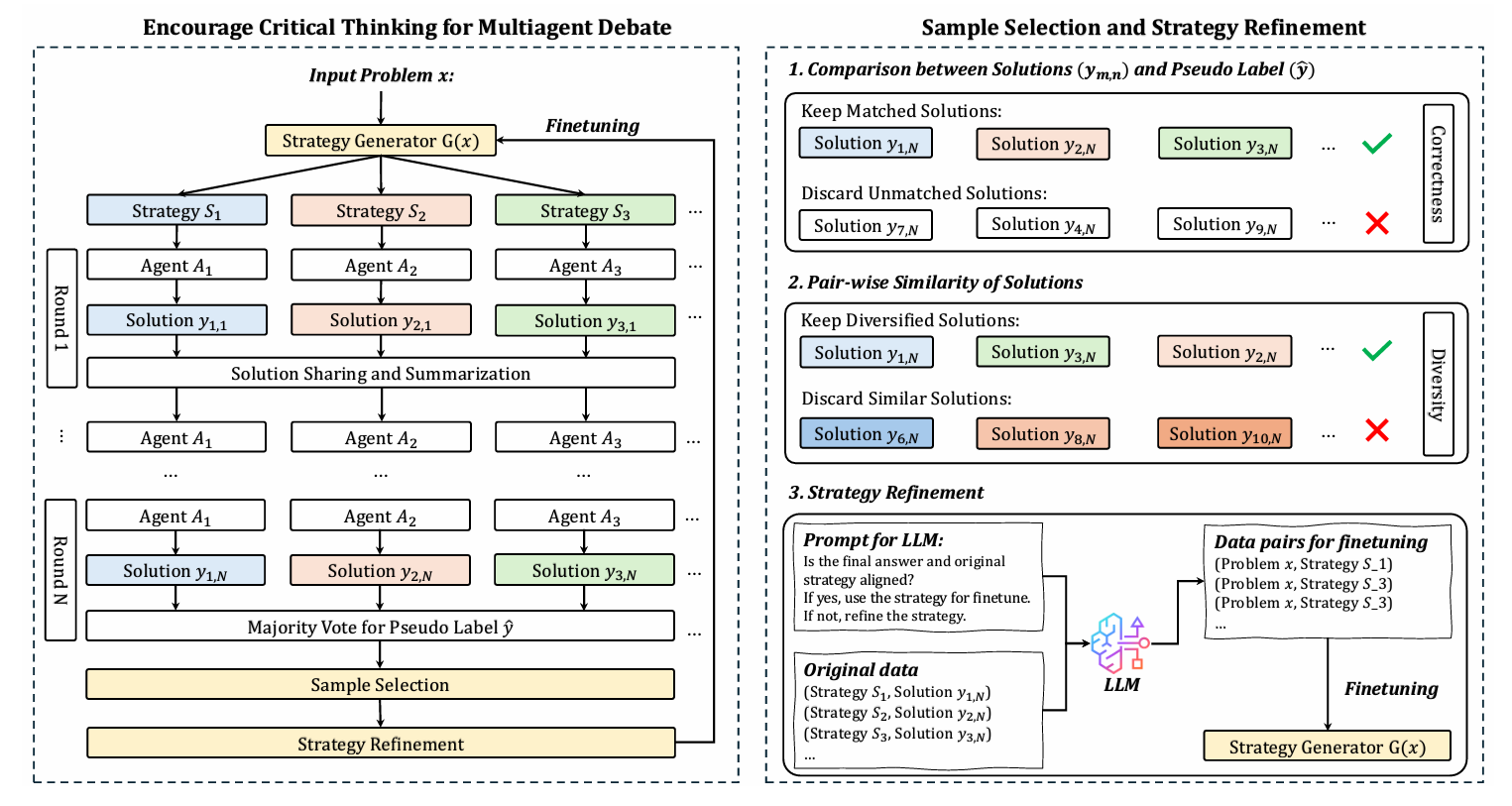
总体框架
整体流程见图 。给定自然语言描述的问题 $x\sim\mathcal{P}_q$,策略生成器 $G(x)$ 先生成一组可能求解的高层策略:
\[S_1,S_2,\ldots,S_M = G(x), \quad x\sim\mathcal{P}_q\]记策略集合为 $S=\lbrace S_i\mid i=1,2,\ldots,M\rbrace $。随后初始化 $M$ 个 LLM 智能体 $\mathbb{A}=\lbrace \mathcal{A}_i\mid i=1,2,\ldots,M\rbrace $。
第一轮辩论中,每个智能体 $\mathcal{A}_i$ 在策略 $S_i$ 条件下生成推理轨迹与答案:
\[y_{i,1}=\mathcal{A}_i(x;S_i),\quad i=1,2,\ldots,M.\]后续轮次,将上一轮所有响应汇总为共享历史 $h_1$,所有智能体基于该历史继续生成。第 $n$ 轮的一般形式为:
\[y_{i,n}=\mathcal{A}_i(x;h_{n-1}),\quad i=1,2,\ldots,M,\quad n=2,3,\ldots,N\]用筛选样本微调策略生成器
为使策略生成器具备批判性思维,需挑选既正确又多样的样本。由于无真值,我们设计无监督指标分别度量正确性与多样性。
正确性筛选:
取最后一轮 $M$ 个答案的多数投票作为伪标签 $\hat{y}$,构建与之一致的集合:
\[\mathcal{D}_c \leftarrow \bigl\lbrace y_{m,N} \mid y_{m,N}=\hat{y},\; m\in\lbrace 1,2,\ldots,M\rbrace \bigr\rbrace\]多样性筛选:
辩论易使轨迹趋同,导致微调收益递减。为此引入多样性度量 $D$,要求满足:
- 渐近正确:均匀分布时最大;
- 有限样本有效;
- 捕捉非线性语义关系。
采用高斯势核(RBF):
\[G_t(u,v)=\mathrm{e}^{-t\mid \mid u-v\mid \mid ^2},\quad t>0\]定义多样性为期望核的对数:
\[D(f;t)=\log\mathbb{E}_{x,y\sim\mathcal{D}_c}\!\Bigl[\mathrm{e}^{-t\mid \mid f(x)-f(y)\mid \mid ^2}\Bigr],\quad t>0\]其中 $f$ 为嵌入模型。
筛选流程:从 $\mathcal{D}_c$ 中依次加入样本,仅当与已选集合的最大核值小于阈值 $\tau$ 时保留:
\[\mathcal{D}_{\mathrm{div}}\leftarrow \lbrace y_1\rbrace \cup\lbrace y_i\in\mathcal{D}_c\setminus\lbrace y_1\rbrace \;\mid \; \max_{y_j\in\mathcal{D}_{\mathrm{div}}}G_t(f(y_i),f(y_j))<\tau\rbrace\]$\tau$ 越大,多样性越高,但可用样本减少。
策略对齐(可选):
初始策略 $S_i$ 可能与最终正确解 $y_{i,N}$ 偏离。引入对齐智能体 $\mathcal{A}_{\mathrm{align}}$,在提示 $P_{\mathrm{ref}}$ 下判断并修正策略:
\[\hat{S}_i=\mathcal{A}_{\mathrm{align}}(S_i,P_{\mathrm{ref}};\hat{y}),\quad i=1,2,\ldots,M.\]最终用高质量三元组 $(x,\hat{S}_i)$ 构成微调数据集 $\mathcal{D}_f$。
批判性思维算法
Require: 问题集 $\mathcal{P}_q$;策略生成器 $G(x)$;$M$ 个智能体;辩论轮数 $N$;微调迭代 $L$;多样性阈值 $\tau$
1: 初始化微调数据集 $\mathcal{D}_f=\emptyset$
2: for $l=1\to L$ do
3: for $x\in\mathcal{P}_q$ do
4: for 轮次 $j=0,\ldots,N$ do
5: $S_1,\ldots,S_M \leftarrow G(x)$ // 生成策略
6: if $j=0$ then
7| $y_{1,1},\ldots,y_{M,1}\leftarrow \mathcal{A}_i(x;S_i)$ // 首轮解
8: else
9: $h_{j-1}\leftarrow$ 汇总上轮响应
10: $y_{1,j},\ldots,y_{M,j}\leftarrow \mathcal{A}_i(x;h_{j-1})$ // 后续轮解
11: end if
12: end for
13: $\hat{y}\leftarrow \mathrm{MajorityVote}(y_{1,N},\ldots,y_{M,N})$
14: $\mathcal{D}_c \leftarrow$ 按公式 (4) 选正确样本
15: $\mathcal{D}_{\mathrm{div}}\leftarrow$ 按公式 (7) 选多样样本
16: $\hat{S}_1,\ldots,\hat{S}_M\leftarrow \mathcal{A}_{\mathrm{align}}(S_i,P_{\mathrm{ref}})$ // 策略对齐
17: $\mathcal{D}_f \leftarrow \mathcal{D}_f \cup \lbrace (x,\hat{S}_i)\rbrace _{i=1}^M$
18: end for
19: $G \leftarrow \mathrm{FineTune}(G,\mathcal{D}_f)$
20: end for
实验
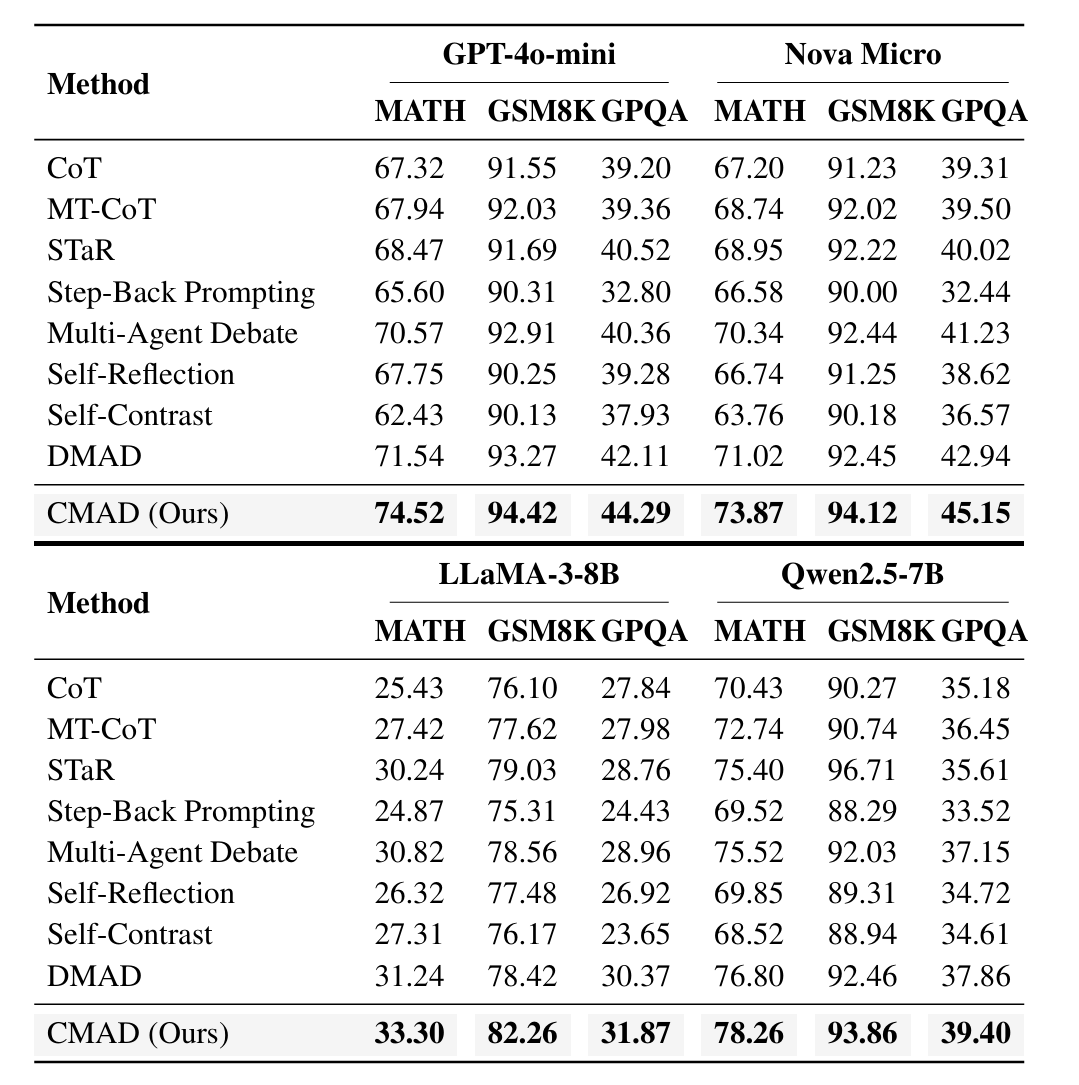
- 在MATH、GSM8K、GPQA三大推理基准上全面领先。
- LoRA微调版本仅训练0.1%参数,性能仍优于全量微调基线。
审稿人意见
策略生成器没讲清楚,有相同的工作,且实验细节缺失,实验报告不一致。
和《Multiagent finetuning of language models》几乎一样。
Self-Directed Discovery: How LLMs Explore and Optimize Configurable LLM Solutions
https://openreview.net/forum?id=c3mE9mXDLn
rating:62222, 不可见
动机
- 行业趋势:金融、医疗、客服等场景越来越倾向于用“通用 LLM 重复推理”代替传统专用模型,因为维护简单。
- 痛点:想让这类系统在生产环境达到“足够好”的效果,目前主要靠专家手工调 Prompt、换模型、加例子,成本高且难以规模化。
- 目标:能否让 LLM 自己完成“设计→评估→分析→改进”的闭环,自动发现更高质量、更低成本的可行配置?
贡献
- 提出一套配置驱动的 LLM-Workflow 描述方法,人类可读、机器可改。
- 实现通用、无人工 Prompt Engineering的 Analyzer-Improver 迭代闭环;只给框架文档+一个例子,就能自动产出可运行 Agent。
- 证明“自指”可行:用来优化任务的 LLM 也可以优化它自己,形成持续累积的改进飞轮。
- 在数学、多选、算法执行三类差异很大的任务上均取得显著增益,显示方法跨领域通用。
方法
核心思路:配置驱动 + 自指迭代
① 配置驱动框架 把任何“LLM 推理任务”都拆成 3 个文件:
- JSON 配置:声明模型、温度、Prompt 模板、输入/输出格式、哪些字段允许被后续优化(modifiability flag)。
- Python 实现:写若干输入预处理函数(特征提取、选例、格式转换等)。
- JSON Schema:定义输入数据接口,保证上下游可拼装。
② 自指迭代闭环(Analyzer-Improver Loop)
- 用另一个“元 LLM”扮演 Analyzer:看当前 Agent 在开发集上的每条对错样本,写一份“错误模式 + 改进建议”的自然语言报告。
- 再用一个“元 LLM”扮演 Improver:读取报告、历史最佳配置、当前配置,生成下一代 JSON+Python。
- 重复 10 轮即可;因为 Analyzer/Improver 本身也是“配置驱动”的 Agent,所以它们自己也可以被继续优化,形成“自指”。
审稿人意见
- 说是agent,但其实就是单次调用,这不叫作agent
- 说是自我提升,但有很多相关的工作,并没发现有什么不同
Few-Shot Idea Auto-Generation: Reasoning Over Idea Representations to Predict New Research Ideas
https://openreview.net/forum?id=R3PdluB82U
南开、南洋理工、港城、Astar
rating:2622,withdraw
目标
用极少量的已有论文作为“种子”,让大模型自动推理并生成可落地的研究新点子。
挑战
- 如何有效表示现有论文的核心思想?
- 如何在过滤不可行想法的同时,生成可落地、可实施的想法?
- 如何有效验证生成的想法?
贡献
- 提出一种想法表示法,通过多智能体提取“梗概+流程画像”来捕获论文核心贡献。
- 设计一个基于 LLM 智能体的生成框架,通过在论文对之间系统化地“架桥”实现交叉授粉。
- 提出一种评估方法:结合语义相似度与“时间加权新颖度评分”,并在 8 个 CS 方向、3353 篇论文上构建基准。
动机
(1) 问题驱动 vs. 缺口驱动 现有方法(CoI、SciAgents、AI Scientist 等)多为问题驱动:先广泛阅读文献→构建想法链→让代理评估新颖性与可行性。该范式资源消耗大,且想法产生过程不透明。相比之下,缺口驱动只需两篇论文,显式地把“一篇的缺口”与“另一篇的贡献”对齐,即可可控地合成新想法(图 2)。我们采用后者。
(2) 想法表示的重要性 现有系统仅用章节级泛泛摘要,不足以识别有意义的研究缺口。我们实验表明:缺乏细粒度表示时,模型难以发现可迁移的创新点。
(3) 实证评估的缺陷 已有研究多让 LLM 按“新颖、可行、意义、清晰、有效”五维打分,或采用共被引、词嵌入距离等代理指标。这些方法要么缺乏前瞻性验证,要么无法追溯想法来源。我们提出基于文献grounded的评估,将生成想法映射到真实学术版图,并给出可调、透明的评分。
方法
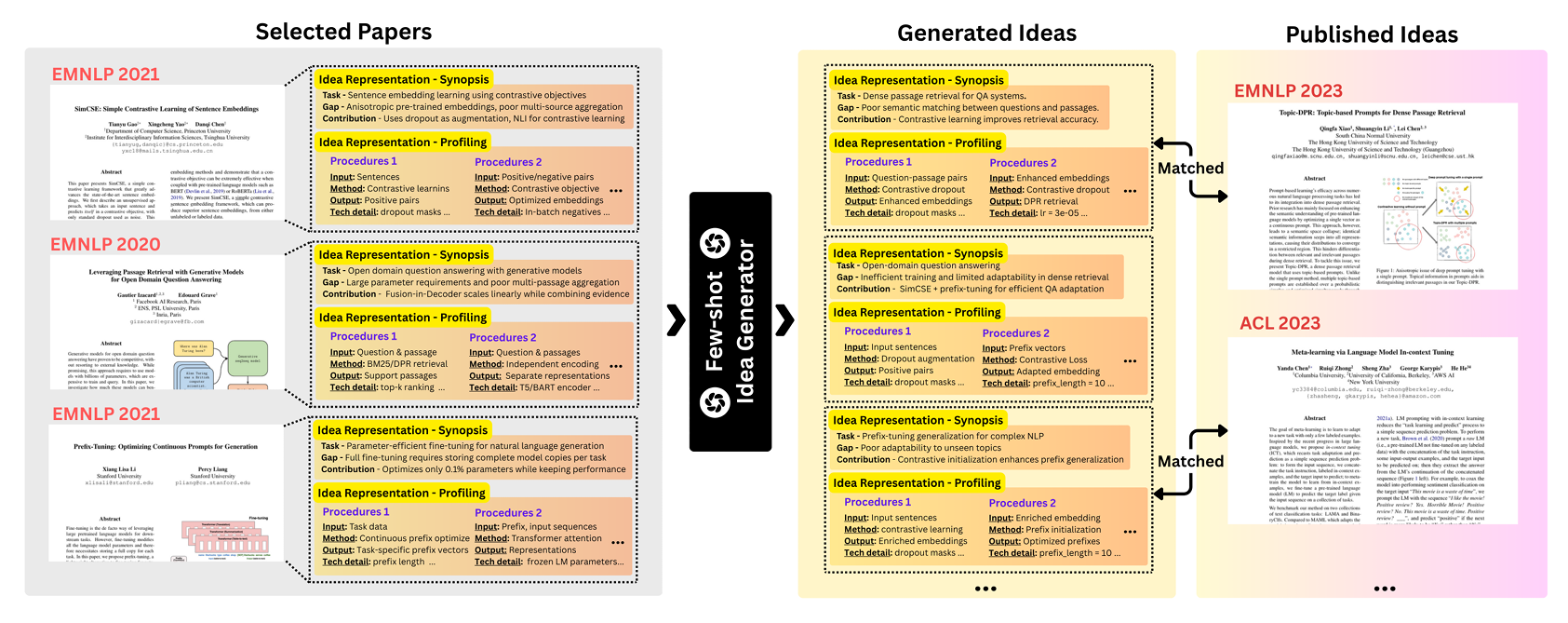
想法表示
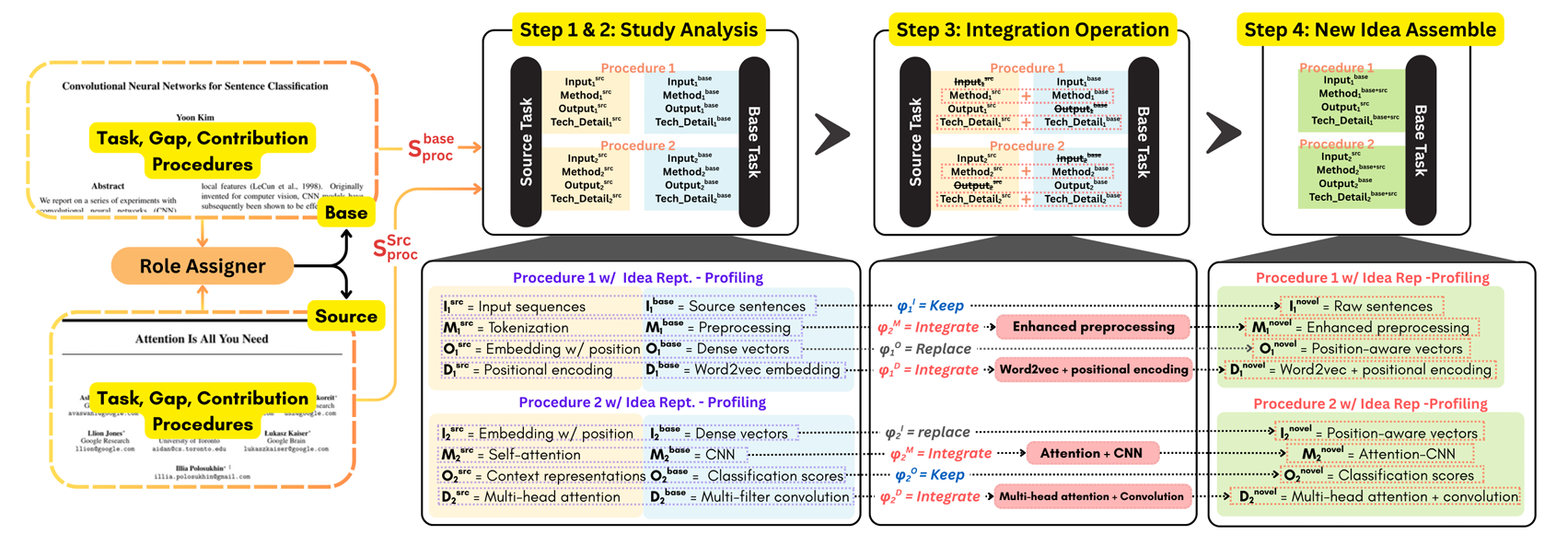
对论文 $P$ 分章节得到 $\mathcal{P}=\lbrace \mathcal{I}, \mathcal{M},\dots\rbrace $($\mathcal{I}$ 为引言,$\mathcal{M}$ 为方法)。目标是输出结构化表示:
\[\mathcal{R}= \lbrace \mathcal{T},\mathcal{G},\mathcal{C}\rbrace \cup\lbrace \mathcal{S}_{\mathrm{proc}}\rbrace\]其中
- $\mathcal{T}$:核心研究任务
- $\mathcal{G}$:识别到的研究缺口
- $\mathcal{C}$:论文贡献
- $\mathcal{S}_{\mathrm{proc}}$:详细流程画像
梗概
用三个函数提取:
\[\begin{aligned} \mathcal{T}&=f_{\mathrm{task}}(\mathcal{I})\\ \mathcal{G}&=f_{\mathrm{gaps}}(\mathcal{I})=\lbrace g_1,g_2,\dots,g_n\rbrace \\ \mathcal{C}&=f_{\mathrm{contrib}}(\mathcal{I},\mathcal{G})=\lbrace (g_i,c_i)\mid g_i\in\mathcal{G},c_i\in\mathcal{C}\rbrace \end{aligned}\]$f_{\mathrm{task}}$ 生成面向行动的描述;$f_{\mathrm{gaps}}$ 列出 2–5 条技术局限;$f_{\mathrm{contrib}}$ 建立“缺口-贡献”显式映射,保证可追溯。
流程画像
从方法章节 $\mathcal{M}$ 提取四元组序列:
\[\mathcal{S}_{\mathrm{proc}}=f_{\mathrm{profile}}(\mathcal{M})=\Big\lbrace \langle I_k,M_k,O_k,D_k\rangle \Bigm| k=1,\dots,K\Big\rbrace\]- $I_k$:输入组件
- $M_k$:方法步骤
- $O_k$:输出规格
- $D_k$:超参、算法、工具等细节
想法生成
角色分配(Role Assignment)
对两篇论文 $\mathcal{P}_1,\mathcal{P}_2$,先让角色分配器 $G_{A_r}$ 决定谁当基座(base)、谁当外援(source):
\[\mathcal{R}^*=G_{A_r}\Big(\lbrace \mathcal{T}_1,\mathcal{G}_1,\mathcal{C}_1\rbrace ,\lbrace \mathcal{T}_2,\mathcal{G}_2,\mathcal{C}_2\rbrace \Big)\rightarrow [\mathcal{R}^{\mathrm{base}},\mathcal{R}^{\mathrm{src}}]\]依据:问题清晰度、贡献新颖度、可迁移性。
交叉授粉生成器
用 Chain-of-Thought 代理按四步执行:
- 基座分析:提取 $\mathcal{R}^{\mathrm{base}}=\lbrace \mathcal{T}^{\mathrm{base}},\mathcal{G}^{\mathrm{base}},\mathcal{C}^{\mathrm{base}}\rbrace \cup\lbrace \mathcal{S}_{\mathrm{proc}}^{\mathrm{base}}\rbrace $
- 外援分析:提取 $\mathcal{R}^{\mathrm{src}}$,聚焦可迁移创新 $\mathcal{S}_{\mathrm{proc}}^{\mathrm{src}}$
- 整合操作:对每对四元组,选择操作 $\psi\in\lbrace \text{integrate},\text{replace},\text{keep},\text{remove}\rbrace $,生成新四元组:
- 新想法组装:遍历所有步骤,得到完整流程 $\mathcal{R}_{\mathrm{proc}}^{\mathrm{novel}}$,输出结构化研究提案。
想法评估
论文相似度
- 将生成想法蒸馏为查询 $Q$(去模型名、留通用算法)。
- 用语义搜索在 OpenAlex 检索候选集 $\mathcal{P}_{\mathrm{retrieved}}$,并排除 parent papers:$\mathcal{P}_{\mathrm{filtered}}=\mathcal{P}_{\mathrm{retrieved}}\setminus\lbrace P^{\mathrm{base}},P^{\mathrm{src}}\rbrace $。
- 计算余弦相似度:
唯一论文比率(Unique Paper Ratio)
在高相似度子集 $\mathcal{P}_{\mathrm{max}}=\lbrace p_j\mid \sigma(\mathcal{Q},p_j)=\max\limits_{p\in\mathcal{P}_{\mathrm{filtered}}}\sigma(\mathcal{Q},p)\rbrace $ 中,按方法聚类,计算:
\[\mathrm{URatio}=\frac{|\mathcal{P}_{\mathrm{unique}}|}{|\mathcal{P}_{\mathrm{max}}|}\]新颖度(Novelty)
设 $y_i$ 为匹配论文 $P_i$ 的出版年,$Y_{\mathrm{max}}$ 为参考集最新年份,$Y_{\mathrm{now}}$ 为当前年。时间因子:
\[t_i=\frac{\max(0,\;y_i-Y_{\mathrm{max}})}{Y_{\mathrm{now}}-Y_{\mathrm{max}}}\in[0,1]\]取 top-k 最相似论文,权重:
\[w_i=\frac{\sigma_i^{\beta}}{\sum_{j=1}^{n}\sigma_j^{\beta}},\quad \sum w_i=1\]最终新颖度:
\[\begin{aligned} \mathsf{Penalty}&=\lambda\sum_{i=1}^{n}w_i\,\sigma_i^{2}\,(1-t_i)^{2}\\ \mathsf{Bonus}&=\alpha\sum_{i=1}^{n}w_i\,\sigma_i\,t_i^{2}\\ N(\mathcal{Q})&=1-\mathsf{Penalty}+\mathsf{Bonus}\in[0,1] \end{aligned}\]$\lambda>\alpha$ 时保守,$\alpha>\lambda$ 时鼓励紧跟最新工作。
实验
| 指标 | Baseline (CoI) | 本文 Full System | 相对提升 |
|---|---|---|---|
| 高相似度(≥0.7)比例 | 8.3 % | 11.7 % | +41 % |
| 高相似度段唯一论文比 | 76.9 % | 78.4 % | 更分散,不扎堆 |
| Novelty 分数 | 0.349 | 0.352 | 持平,不牺牲新颖 |
- 成本:用 GPT-4o-mini 全流程,每生成一个点子 0.0075 美元,比直接用 GPT-4o 便宜 8×。
- 人工双盲评测:16 位领域博士打分,96.6 % 一致同意生成点子“有意义”。
用法
把 3–5 篇你最关心的论文丢进去,系统会返回:
- 一张“缺口-贡献”对照表;
- N 条可执行的新研究流程(含输入、算法、输出、超参);
- 每条流程的“前瞻性得分”与最相关的未来论文。
审稿人评价
- 有相似的工作:SciAgents
- 创新性评估存在缺陷
- 评估指标有待商榷
A Problem-Oriented Perspective and Anchor Verification for Code Optimization
https://openreview.net/forum?id=HGaUV3jjvo
浙江大学
rating:6664, Accept
动机
传统方法(如 PIE)是基于用户视角(User-Oriented),即:同一个程序员对同一个问题逐步提交优化版本,形成优化对(slow → fast)。但这种方法受限于个人思维惯性,优化往往是局部、渐进的。
本文提出问题导向视角(Problem-Oriented),即:将所有程序员对同一问题的提交按运行时间排序,构建跨用户的优化轨迹。这样可以从不同程序员的多样解法中提炼出更本质、更全局的优化策略。
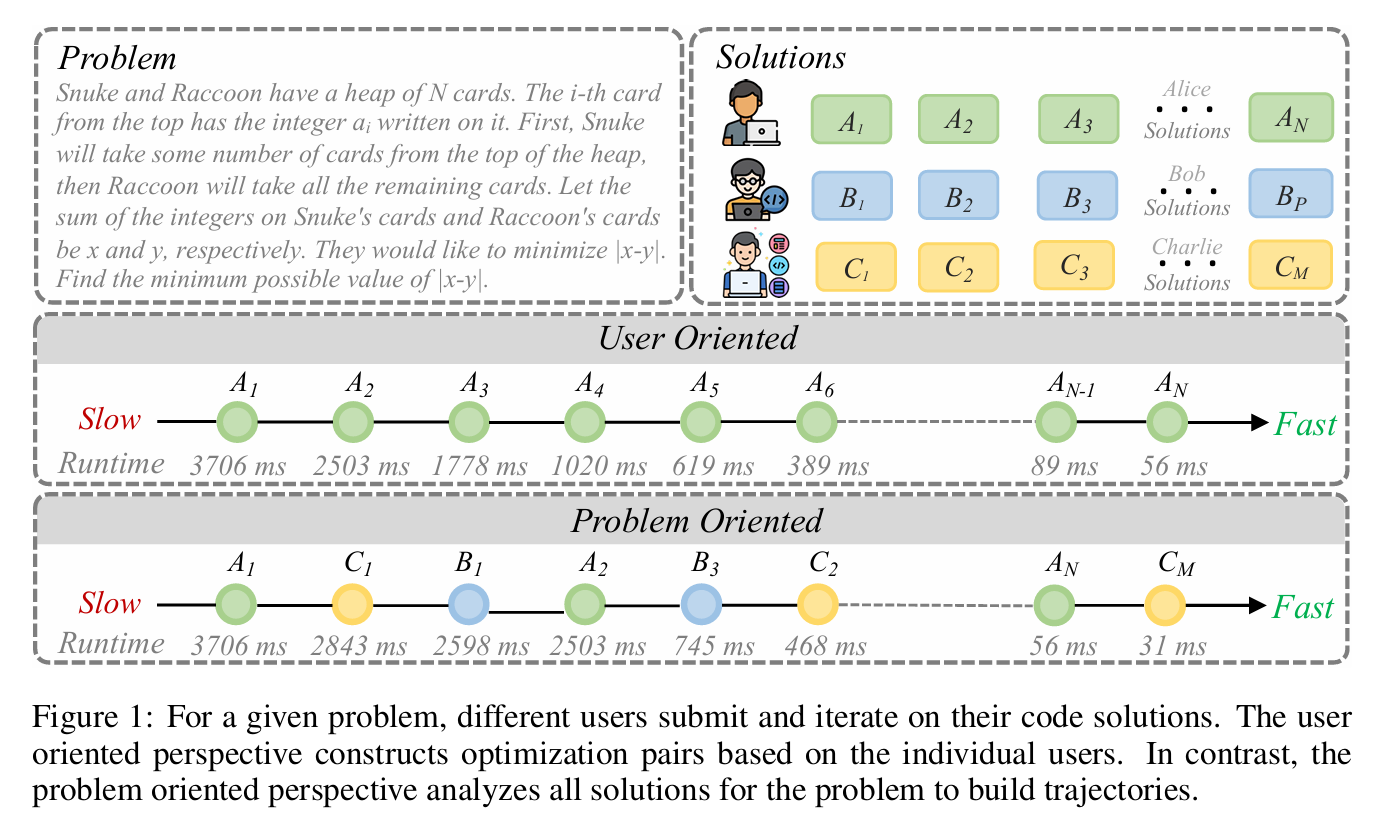
问题导向的代码优化
问题导向优化对
用户导向视角
当前研究中的代码优化对来自 PIE 数据集,该数据集基于同一程序员在同一题目上的迭代提交。 设共有 $P$ 道题目,第 $p$ 道题有 $U_p$ 个用户提交,用户 $u$ 的合法提交序列为
\[[A^{(u)}_1,\; A^{(u)}_2,\; \dots,\; A^{(u)}_{n_u}]\]则用户导向优化对为相邻提交构成的集合
\[\Bigl\lbrace \bigl(A^{(u)}_i,\; A^{(u)}_{i+1}\bigr)\Bigr\rbrace _{i=1}^{n_u-1},\quad \forall u,\;\forall p.\]所有用户的所有相邻对聚合后即为 PIE 数据集。
问题导向视角
我们将同一题目 $p$ 下所有用户的合法提交按运行时间升序排列,得到跨用户的优化轨迹
\[[A_1,\; C_1,\; B_1,\; A_2,\; B_3,\; C_2,\; \dots,\; C_M].\]由此构造优化对
\[\Bigl\lbrace \bigl(X_i,\; X_j\bigr)\Bigm| i<j,\; X_i,X_j\in\text{所有合法提交}\Bigr\rbrace .\]记每道题最终保留的优化对数量等于 PIE 中该题目的对数,以保证实验公平。
缓解数据稀缺
设每道题有 $U$ 个用户,每个用户平均 $n_u$ 次合法提交。 用户导向优化对总数
\[N_{\text{user}}=\frac12\sum_{p=1}^P\sum_{u=1}^{U_p}(n_u-1)\approx\frac12\sum_{p=1}^P U_p\cdot\overline{n_u}.\]问题导向优化对总数
\[N_{\text{problem}}=\frac12\sum_{p=1}^P\binom{\sum_{u=1}^{U_p}n_u}{2}\approx\frac12\sum_{p=1}^P\frac{(U_p\cdot\overline{n_u})^2}{2}.\]当 $U_p\ge10$ 时,$N_{\text{problem}}$ 比 $N_{\text{user}}$ 高一个数量级,显著缓解数据稀缺。
多维分析
我们在相同规模(78 k 对)下比较 PIE(用户导向)与 PCO(问题导向):
| 维度 | 指标 | 结论 |
|---|---|---|
| 结构差异 | 控制流图编辑距离(GED) | PCO 平均 GED 显著更大,表明常涉及全局算法改动 |
| 语义差异 | CodeT5+ 嵌入 + t-SNE | PCO 嵌入点更分散,说明语义多样性更高 |
| 人工抽样 | 优化类型分类 | PCO 中 78 % 为全局算法优化,PIE 仅 19 % |
使 LLM 适应优化对
评测指标
- %OPT:测试集中被加速且正确的比例(加速 $\ge10\%$)
-
SPEEDUP:平均加速比
\[\text{SPEEDUP}(o,n)=\frac{o}{n},\quad \text{失败时取 }1.0\] - CORRECT:测试集中功能等价的比例
实验设置
- 模型:CODELLAMA-13 B、DeepSeek-Coder-7/33 B、Qwen2.5-Coder-7/32 B
- 解码:temperature=0.7,BEST@k(k=1 或 8)
- 编译:g++-9.4,flag=`-O3 -std=c++17`,gem5 模拟器测时
主要结果(BEST@1)
| 模型 | 数据集 | %OPT | SPEEDUP | CORRECT |
|---|---|---|---|---|
| Qwen2.5-Coder-32 B | PIE | 31.24 % | 2.95× | 46.52 % |
| Qwen2.5-Coder-32 B | PCO | 58.90 % | 5.22× | 61.55 % |
进一步分析
PCO 比例实验
随机抽取 10 %–100 % 的 PCO 对训练 Qwen2.5-Coder-32 B:
- 30 % 的 PCO 对即可在 %OPT 与 SPEEDUP 上全面超越完整 PIE
- 50 % 的 PCO 对即可在 CORRECT 上追平完整 PIE
视角 vs 选择效应
控制实验(Qwen2.5-Coder-7 B,同一超参)
| 数据集 | 构造方式 | %OPT | SPEEDUP | CORRECT |
|---|---|---|---|---|
| PIE | 原始用户导向 | 26.96 % | 2.80× | 41.21 % |
| PCO-Random | 问题导向+随机采样 | 49.55 % | 4.56× | 53.23 % |
| PCO-Top | 问题导向+高速优先 | 54.83 % | 4.73× | 56.26 % |
结论:视角本身是性能提升的主因,高速优先采样仅进一步精炼。
编辑模式可迁移性
对 PCO 进行 GED 分层实验(每题选 40 % 对):
| 子集 | %OPT | SPEEDUP | CORRECT |
|---|---|---|---|
| PCO-High-GED | 46.23 % | 4.48× | 50.43 % |
| PCO-Low-GED | 36.49 % | 3.75× | 42.43 % |
| PCO-Random | 40.32 % | 4.11× | 46.94 % |
High-GED 对并未造成学习困难,反而使模型学到更具迁移性的算法改进模式(如前缀和、哈希、差分等)。
面向实用性的锚点验证框架
LLM 代码优化固有的关键挑战:无论采用指令提示还是微调,优化后的代码都无法保证 100 % 正确,我们称这一现象为优化税(optimization tax)。为应对该挑战,提出锚点验证框架(Anchor Verification Framework),利用原始“慢但正确”的代码作为金标准锚点,生成可信测试用例并迭代精炼优化代码。
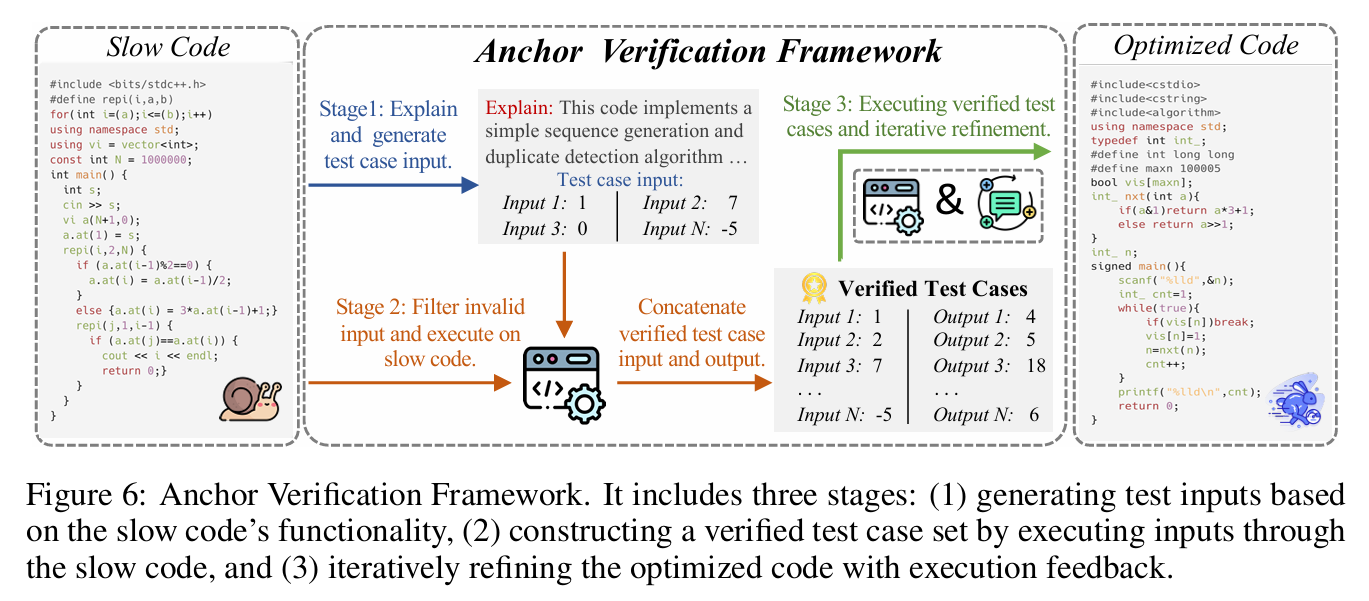
与通用代码生成中依赖可能出错的合成测试用例不同,代码优化场景具有独特优势:待优化的原始代码虽然低效,但功能正确,因此可直接作为测试用例的可靠锚点。框架整体流程如图 6 所示,共分三阶段:
阶段 1:测试输入生成
给定慢代码 $S$,提示 LLM 解释其功能并生成仅包含输入的测试用例集合
\[\mathcal{I}=\lbrace x_1,x_2,\dots,x_k\rbrace ,\quad k=3\;(\text{默认}).\]与直接生成完整用例相比,仅生成输入可降低 LLM 负担,避免输出错误。
阶段 2:构造已验证测试用例
将 $\mathcal{I}$ 输入到慢代码 $S$ 真实执行,得到对应输出
\[y_i=S(x_i),\quad i=1,\dots,k.\]过滤格式不符的输入后,获得已验证测试用例集
\[\mathcal{T}=\bigl\lbrace (x_i,y_i)\bigr\rbrace _{i=1}^k.\]阶段 3:迭代精炼
用 $\mathcal{T}$ 检验优化代码 $F$:
- 若 $F(x_i)\ne y_i$,将编译/运行错误信息反馈给 LLM,要求其修正 $F$;
- 最多迭代 $T$ 次(实验取 $T=1$ 或 $5$)。
反馈提示模板示例:
### 错误信息
{编译或运行时错误}
### 需修正的优化代码
{F的当前版本}
### 要求
请根据上述错误修正代码,确保通过所有已验证测试用例。
审稿人意见
扩展到现实软件工程场景如输入输出瓶颈、内存管理、API使用以及与大型代码库的交互中表现有待考究。
AutoPBO: LLM-powered Optimization for Local Search PBO Solvers
https://openreview.net/forum?id=mpwnjHxtBP
rating:242022246(审稿人好多), Reject
背景
伪布尔优化(PBO)问题:一种组合优化问题,目标是在满足一组伪布尔约束的前提下,最小化一个线性目标函数。
求解方法:
- 完备方法:如MIP求解器(Gurobi、SCIP)和SAT-based方法,能保证最优解,但对大规模问题效率低。
- 不完备方法:如局部搜索(Local Search, LS),求解速度快,但依赖人工设计的启发式策略,调优成本高。
贡献
1. 提出AutoPBO框架
- 首次将LLM用于PBO局部搜索求解器的自动化优化。
- 采用多智能体协作机制(Code Optimization Planner、Code Editor、Modification Evaluator)迭代优化求解器中的关键函数。
- 引入贪心策略,逐步优化各个函数模块,避免模块间冲突。
2. 设计StructPBO求解器
- 为便于LLM理解和优化,提出一个结构化、模块化的PBO局部搜索求解器。
- 将求解器分解为7个独立函数(如CalculateScore、UpdateWeights、PickEscapeVariable等),支持逐模块优化。
方法
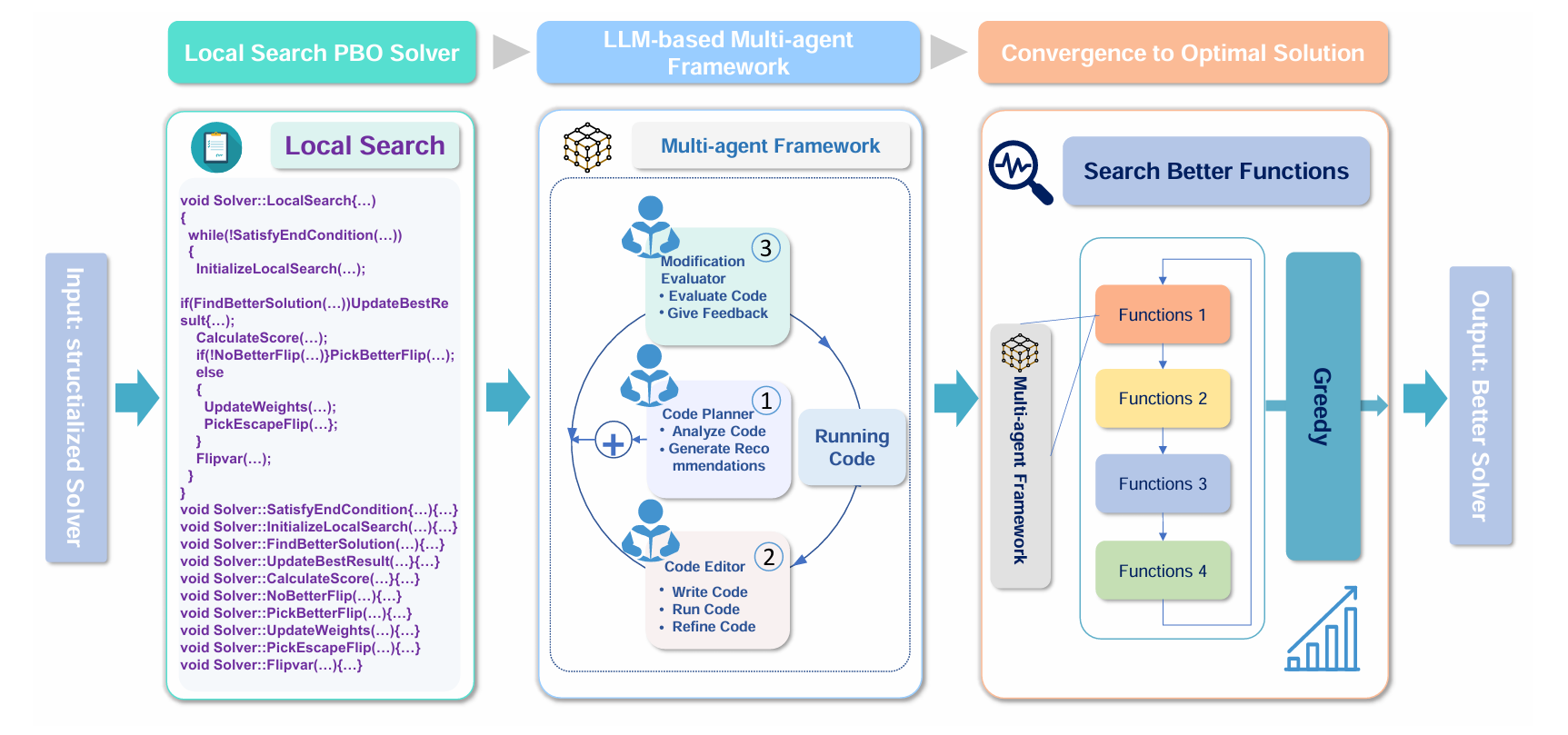
如图所示,框架首先加载一个局部搜索 PBO 求解器,随后启动多轮代码优化。每一轮中,我们并行地执行若干次独立的代码修改任务,每次任务由三个 LLM 智能体协作完成。一轮优化结束后,生成多个代码版本,并通过贪心策略选出表现最优的版本作为下一轮输入。重复此过程,最终得到优化后的求解器。
多智能体优化
框架中包含三个专用 LLM 智能体,各自承担不同角色:
- Code Optimization Planner:分析关键代码片段,识别待优化的函数,并生成修改方案。
- Code Editor:根据 Planner 的建议,实际修改代码以提升性能。
- Modification Evaluator:评估修改后的代码,并生成后续改进建议。
三者通过“规划—编辑—评估”的闭环自动循环工作。
一个代码优化轮次分为两个阶段:
- 规划阶段:Planner 智能体提出优化建议,例如:
- “动态分数比例:根据当前搜索状态自适应调整
hscore与oscore的权重,当解不可行时提高硬约束权重。” - “引入变量年龄项:在评分函数中加入变量自上次翻转以来的时间,鼓励多样化以逃离局部最优。”
- “动态分数比例:根据当前搜索状态自适应调整
- 编辑阶段:Editor 与 Evaluator 多次交互:
- Editor 首先根据建议修改代码,排除如变量重命名、参数微调等无意义变动,并尝试编译运行,收集报错或运行信息。
- Evaluator 对代码进行语义与性能评估,反馈给 Editor。
- 多次迭代后,输出本轮最终代码版本。
提示工程
我们为三个智能体设计了结构化提示,遵循 OpenAI 指南,包含:
| 智能体 | 任务 | 提示要点 |
|---|---|---|
| Planner | 1. 全面分析关键代码段 2. 提出可行且理论上有前景的修改方案 |
1. 完整阅读相关代码 2. 生成实用且理论上有效的建议 3. 严格遵循 JSON 格式输出 |
| Editor | 阶段1:准确理解 Planner 描述,提出代码修改方向 阶段2:分析实验结果,生成更优版本 |
阶段1:保留函数签名,不引入未定义变量,确保与旧代码有实质差异 阶段2:保持代码格式,避免重复修改 |
| Evaluator | 评估并分类修改效果 | 1. 仔细语法检查 2. 对比分析是否带来有意义提升 3. 分类记录结果 |
所有提示统一以“一名试图改进 PBO 启发式函数的求解器研究者”身份开头,确保上下文一致。
收敛至最优解
实现了一种迭代贪心算法,通过以下三步逐步构建更优求解器:
- 代码优化轮次:每次只优化一个函数,其余固定。
例如,先对
UpdateWeights生成多个版本,并行运行后在训练集上比较:- 记录每个版本的 可行解数量(Feasible count)
- 记录 优于 StructPBO 的实例数(Win count)
- 选出两项指标总和最高的版本进入下一步
-
修改传播:将当前最优函数(如改进后的
UpdateWeights)立即集成到 StructPBO 中,后续优化(如CalculateScore)在此基础上进行,确保模块间一致性。 - 迭代改进:重复上述过程,直到所有目标函数都被优化过。
这种顺序式贪心策略避免了函数间耦合导致的冲突,例如 CalculateScore 必须基于 UpdateWeights 最新权重分布进行评分,若独立优化后拼接,可能因权重不一致而失效。
新型结构化局部搜索 PBO 求解器:StructPBO
现有局部搜索 PBO 求解器(如 NuPBO)结构复杂、模块耦合高,直接交给 LLM 优化易产生语法错误或逻辑混乱。为此,我们设计了 StructPBO,一个模块化、易读、易改的 PBO 局部搜索框架。
StructPBO 的整体流程见:
\caption{Algorithm 1: the StructPBO solver}
\begin{algorithmic}[1]
\Require PBO instance $F$, cutoff time \textit{cutoff}
\Ensure Best solution $\alpha^*$ and its objective value $obj^*$, or "No solution found"
\State $\alpha^* \gets \emptyset,\quad obj^* \gets +\infty$
\State $\alpha \gets \text{InitializeAssignment}()$
\While{\textrm{elapsed time} < \textit{cutoff}}
\If{$\alpha$ is feasible and $obj(\alpha) < obj^*$}
\State $\alpha^* \gets \alpha,\quad obj^* \gets obj(\alpha)$
\EndIf
\For{each variable $x$}
\State $hscore(x) \gets \Delta\text{Penalty}_{\text{hard}}(x)$
\State $oscore(x) \gets \Delta\text{Penalty}_{\text{obj}}(x)$
\State $score(x) \gets \text{CalculateScore}(hscore(x), oscore(x))$
\EndFor
\State $D \gets \lbrace x \mid score(x) > 0\rbrace $
\If{$D \neq \emptyset$}
\State $x \gets \text{PickBestVariable}(D)$
\Else
\State \text{UpdateWeights}(F)
\State $x \gets \text{PickEscapeVariable}(F)$
\EndIf
\State $\alpha \gets \alpha$ with $x$ flipped
\EndWhile
\If{$\alpha^* \neq \emptyset$}
\Return $\alpha^*, obj^*$
\Else
\Return \text{No solution found}
\EndIf
\end{algorithmic}
StructPBO 将求解器分解为 7 个独立函数:
| 函数名 | 功能 |
|---|---|
InitializeAssignment |
启发式生成初始完整赋值 |
Penalty_hard |
计算翻转变量对硬约束惩罚的减少量 |
Penalty_obj |
计算翻转变量对目标函数惩罚的减少量 |
CalculateScore |
将上述两项组合为动态复合分数 |
PickBestVariable |
根据分数选择最优翻转变量 |
UpdateWeights |
动态调整硬约束与目标函数的权重 |
PickEscapeVariable |
当陷入局部最优时,选择变量进行多样化逃逸 |
这种模块化设计使得 LLM 可以逐函数优化,而不破坏整体一致性,为 AutoPBO 提供了理想输入。
实验结果
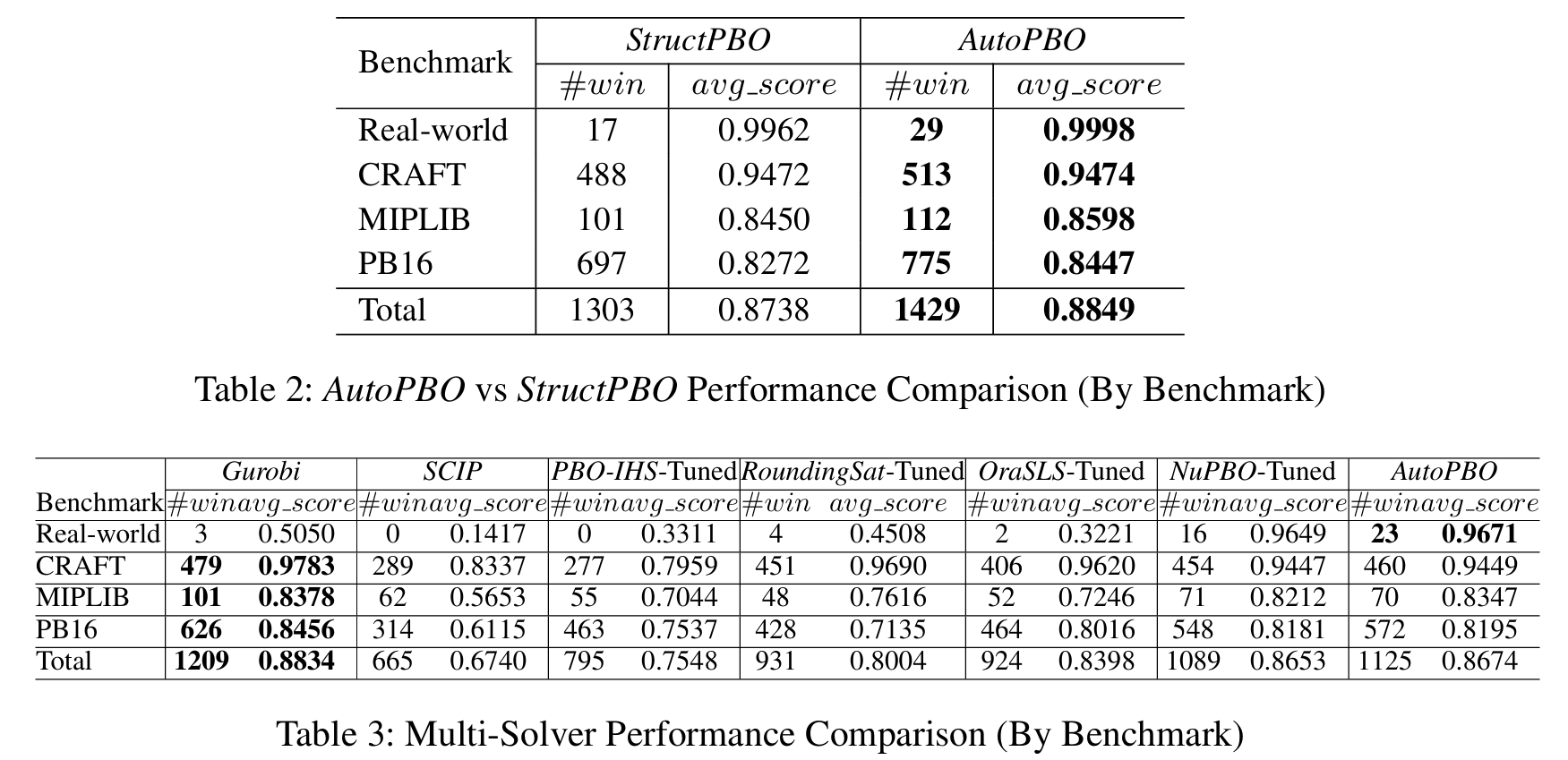
审稿人意见
写作混乱、数学细节不清晰、没有创新、高度依赖求解器、实验不足、通用性受限
Discovering Architectures via an Evolutionary Agentic Framework
https://openreview.net/forum?id=ndHE6IfOnw
rating:44424, Reject
动机
在科学发现这类长周期、复杂任务中,大语言模型(LLMs)迄今大多只是人类研究者的“助手”,而非能够从假设到发现全程主导创新的自主智能体。本文尝试让 LLM 不仅端到端地走完整个科研 workflow:提出新想法、编写代码、做实验、分析结果,还能从实验反馈中进化策略。
痛点
理想中的“AI 科学家”(AI Scientist)应能独立完成整个科研循环,但现有系统往往只能充当“副驾驶”:
- 上下文窗口有限,难以跟踪长周期实验
- 缺乏来自真实训练环境的丰富、可交互反馈
- 只能完成写代码、检索等离散子任务
近期一些工作(如 AlphaFold、AlphaGeometry)实现了特定领域的全自动化,但它们通常依赖简化环境,与真实科研场景差距较大。
框架
ASI-ARCH 框架通过三种专职智能体协同完成上述闭环:
- Researcher:提出新架构并写代码
- Engineer:负责训练与评估
- Analyst:总结实验洞察,指导下一次迭代
在线性注意力这一极具挑战的领域验证了该方法。经过 1 773 次完全自主的实验,LLM 智能体发现了 105 个全新架构,在多种规模与基准上均优于现有 SOTA。此外,我们对智能体自发涌现的设计模式进行了系统分析,为社区提供了可借鉴的洞察。代码与全部模型已开源。
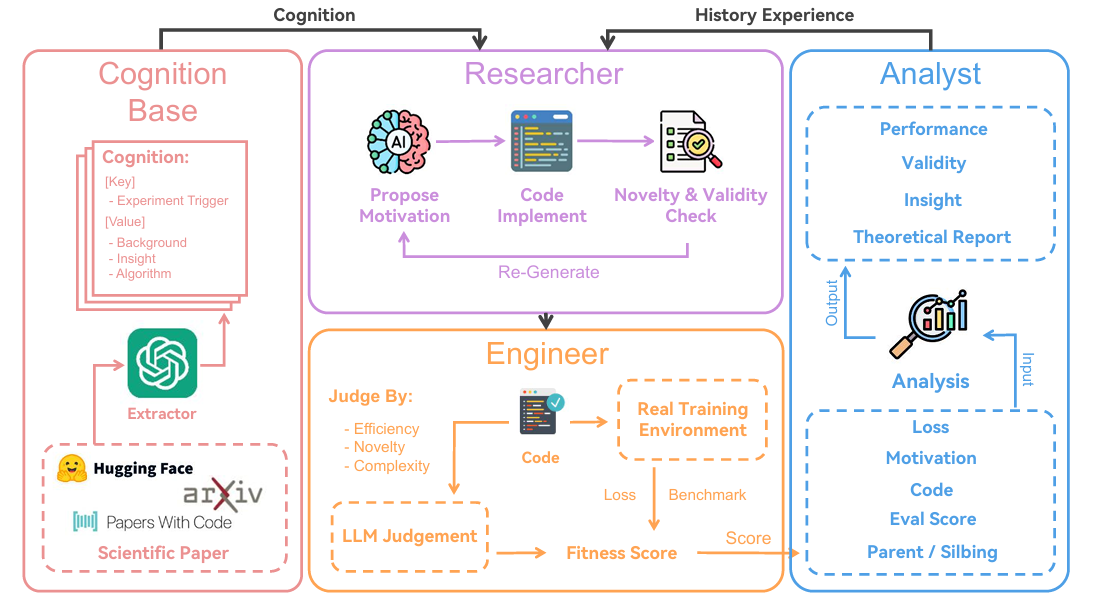
框架包含 4 个模块,形成进化闭环:
- Researcher(紫色):从历史数据提出新架构
- Engineer(橙黄):训练并返回客观指标
- Analyst(蓝色):结合Cognition 知识库(红色)生成洞察
- Cognition:蒸馏自 100 篇线性注意力经典论文的结构化知识
每轮迭代后,候选池更新,仅保留 top-50 架构作为下一轮“父母”。整个系统完全自循环,无需人类干预。
方法
受人类科学家工作流启发,ASI-ARCH 被设计为一个闭环自主架构发现系统。 框架由三大核心角色组成:
- Researcher:提出新架构
- Engineer:在真实环境中训练并评估
- Analyst:分析结果、提取洞察,供下一轮使用
整个进化过程让后续设计直接继承并放大过往成功经验。 系统通过两条关键途径实现“从经验中学习”:
- 统一适应度分数(fitness score)——量化每个架构的优劣,为进化提供明确目标;
- 双源知识注入——既蒸馏人类专家文献(Cognition),也总结自身实验历史(Experience),共同指导下一次设计。
适应度函数
传统方法往往只看定量指标(训练 loss、 benchmark 分数),易被“奖励黑客”或“过拟合个别 benchmark”带偏。 我们引入定性+定量的复合适应度:
\[\displaystyle \text{Fitness} = \underbrace{\frac{1}{3}\Big[\sigma(\Delta_{\text{loss}})+\sigma(\Delta_{\text{benchmark}})\Big]}_{\text{Quantitative}} + \underbrace{\frac{1}{3}\text{LLM}_{\text{judge}}}_{\text{Qualitative}}\]其中
- $\Delta_{\text{loss}}$、$\Delta_{\text{benchmark}}$ 为新架构相对于基线(DeltaNet)的相对改善;
- $\sigma(\cdot)$ 为 sigmoid 映射,放大微小但显著的改进,同时封顶极端值;
- $\text{LLM}_{\text{judge}}$ 由固定 prompt 的独立 LLM evaluator在 1–10 分区间给出主观建筑质量评分,线性归一化到 $[0,1]$。
该复合分数兼顾“跑分”与“建筑美学”,与人类专家直觉对齐。
Researcher:提出新架构
Researcher 模块的目标有两个:
- 高质量创新:避免平凡改动;
- 避免重复:减少算力浪费。
为此我们设计 4 个协同机制:
(1) 种子选择(Seed Selection)
维护一个全局候选池(容量 50),保存历史分数最高的架构。 每轮进化采用两级采样:
- 从 top-10 中随机选 1 个“父母”直接做变异;
- 从 11–50 名中再抽 4 个“远亲”提供多样化参考。
(2) 动态上下文(Flexible Context)
历史实验的自然语言描述(动机、实现、分析)可能很长。 每次进化前,用低温度 LLM 现场生成 1–2 句浓缩摘要,不缓存。 摘要的微小差异迫使 Researcher 以不同视角看待同一段历史,从而增加多样性。
(3) 一体化实现(Integrated Implementation)
传统做法把“设计”与“写代码”拆成两个模型,导致实现漂移(implementation drift)——代码与初衷不符。 ASI-ARCH 让同一个 LLM 先写设计动机,再立即写代码,全程保持上下文一致,显著降低漂移。
(4) 新颖性与合理性预检(Novelty & Sanity Check)
训练前做两道过滤:
- 文本层面:用 embedding 检索 top-5 最相似历史动机,再让 LLM 判断是否实质性重复;
- 代码层面:运行轻量静态检查(复杂度红旗、掩码模式等),拦截常见设计陷阱。
未通过者将收到具体反馈,由 Researcher 自行重写,不浪费 GPU。
Engineer:训练与评估
Engineer 模块负责在真实 GPU 环境中跑通代码,返回客观指标供计算适应度。 评估分两步:
(1) 真实代码环境(Real Code Environment)
- 给 LLM 可交互的 Python 运行时,直接执行其生成的 PyTorch 代码;
- 出错时把报错日志 + 设计动机一并返回,让 LLM 自行 debug、迭代修正;
- 监控训练轨迹,异常 loss、编译超时、病态速度 等情况立即终止,防止浪费。
(2) LLM-as-Judge 主观评分(LLM-as-Judge Scoring)
- 用固定 prompt的独立 LLM 对架构进行 1–10 分主观评价;
- 评价维度:性能上下文、复杂度、计算效率、与基线相比的新颖性;
- 分数经线性映射到 $[0,1]$ 后纳入适应度。
Analyst:挖掘实验洞察
Analyst 模块在每轮实验结束后,指出当前架构的优劣,并给出下一步改进方向。 分析依赖两条知识源:
(1) Cognition 知识库
- 预先蒸馏约 100 篇线性注意力经典论文,结构化存储为“cognition”三元组:
(适用场景,核心算法,历史背景) - 用嵌入检索取最相关的 3 条 cognition,作为“人类专家提示”供 Researcher 下一轮参考。
(2) 上下文对比分析(Contextual Analysis)
- 把当前架构与亲代、兄弟节点做对比,近似做消融实验;
- 通过结构相似但性能差异反推各模块贡献,定位关键设计元素。
Analyst 的输出(优势、劣势、下一步建议)直接写入历史库,成为下一轮进化的“经验”。
实验
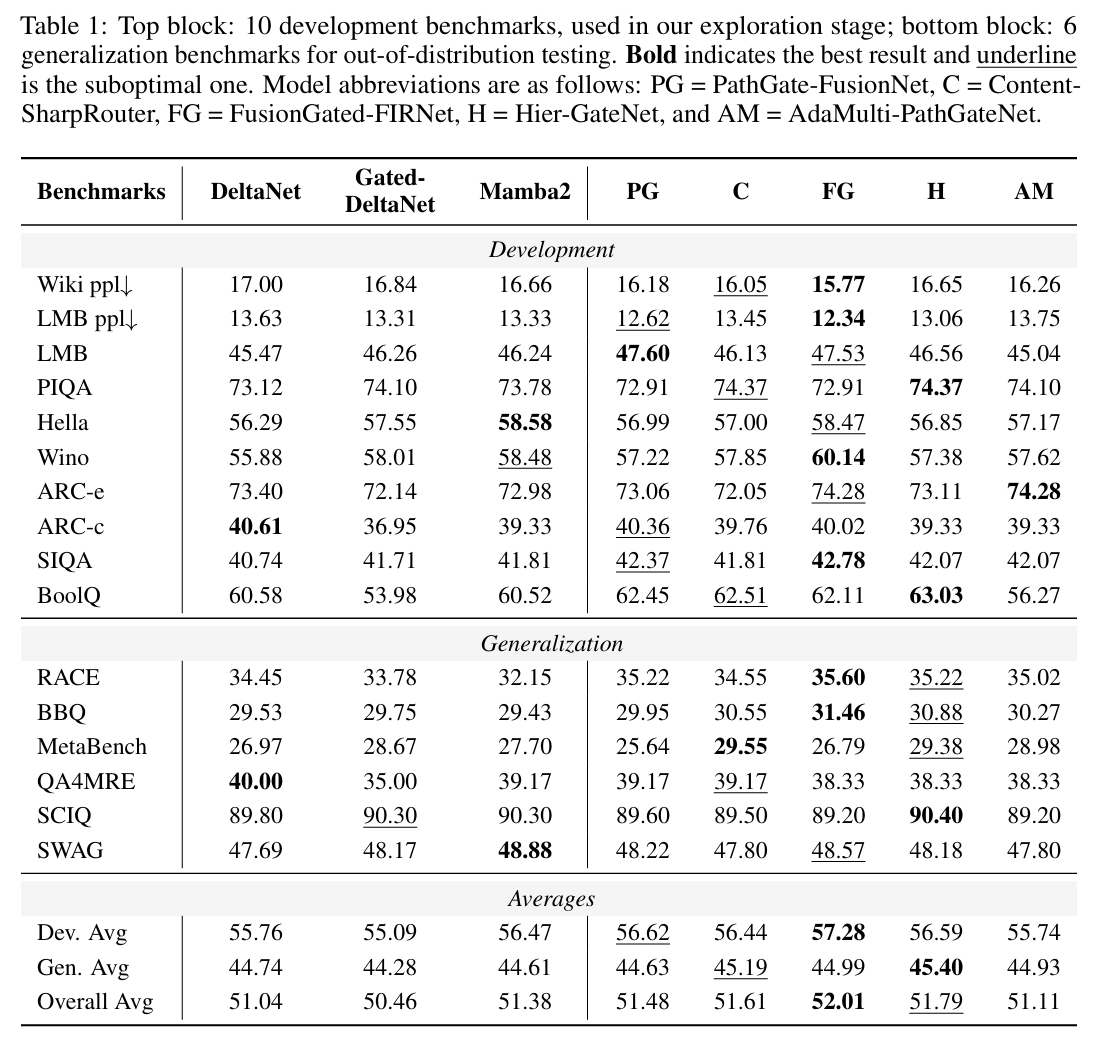
审稿人意见
- LLM生成的方法改进都比较小,而且没有可解释性
- 框架的每个部分都有人工设计
- 方法的评分比较随意
- 没有消融