ICLR 2026 review阶段,LLM AHD合集四
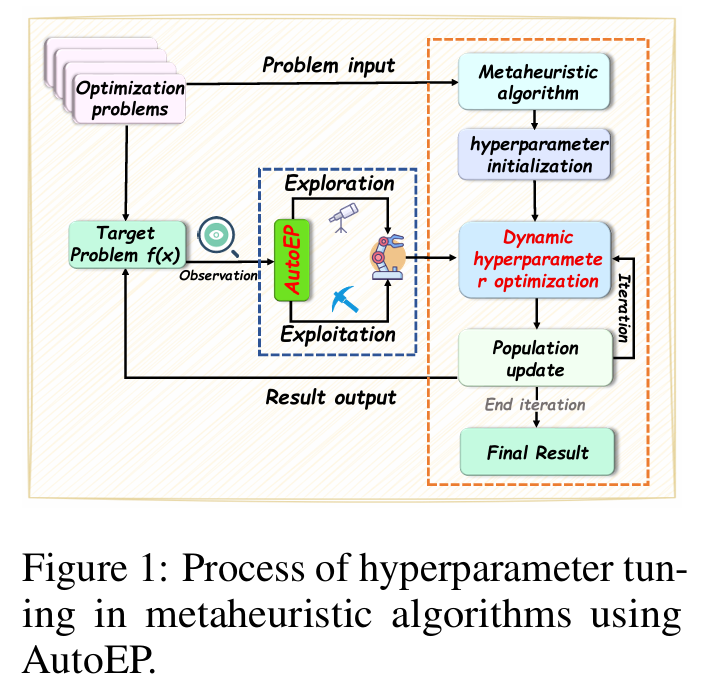
AutoEP: LLMs-Driven Automation of Hyperparameter Evolution for Metaheuristic Algorithms
https://openreview.net/forum?id=hit3hGBheP
国防科大
rating:8666, Accept, Oral
背景
元启发式算法(如遗传算法 GA、粒子群优化 PSO、蚁群算法 ACO)在解决复杂组合优化问题中表现优异,但其性能高度依赖于超参数设置。传统方法依赖人工经验或强化学习(RL)来调节这些参数,但存在以下问题:
- 人工方法:规则僵化,难以泛化;
- RL 方法:训练成本高、样本效率低、泛化能力差。
贡献
核心贡献:AutoEP 框架
AutoEP 是一种基于大语言模型(LLM)的零样本超参数自动调节框架,无需训练即可实时调节算法参数。其核心思想是:
用 LLM 替代训练过程,用“推理”替代“学习”。
- 零样本算法控制新范式:我们提出了一种无需训练的通用框架,LLM 作为“可插拔”推理核心,动态控制算法超参数,适用于任何元启发式算法,无需修改或重训练。
- 基于搜索轨迹分析的 LLM 推理接地机制:为避免幻觉并确保数据驱动决策,我们将 LLM 的推理锚定在实时搜索轨迹的实证证据上。通过持续提供 ELA 特征(如适应度分布、解多样性、搜索难度估计等),LLM 能感知当前优化状态,从而做出有依据的超参数调整。
- 多 LLM 协作的复杂推理能力:我们展示了一个由多个小型开源 LLM(如 Qwen-72B、DeepSeek-67B)组成的协作流水线,能够有效分解并解决复杂控制任务。实验表明,该方法的性能可与大规模专有模型(如 GPT-4)媲美,同时推理延迟显著降低,提升了可访问性、可复现性与效率。
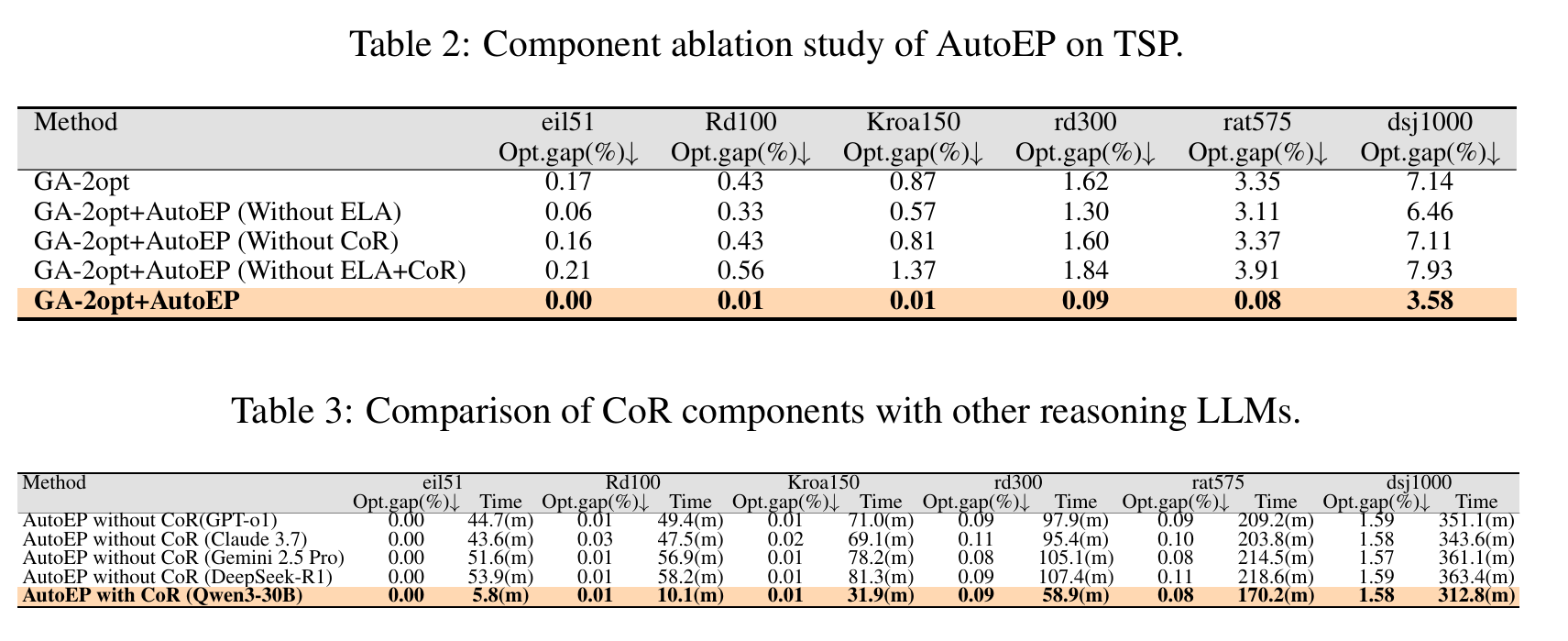
- 跨基准问题的 SOTA 性能:我们在三种元启发式算法(GA、PSO、ACO)与四个组合优化问题上进行了广泛实验,结果表明 AutoEP 一致且显著地优于传统调参方法与近期基于 LLM 的方法。尤其值得注意的是,我们的框架使开源模型 Qwen3-30B 达到了与 GPT-4 相当的性能,展示了自动化超参数设计的新范式。
方法概括
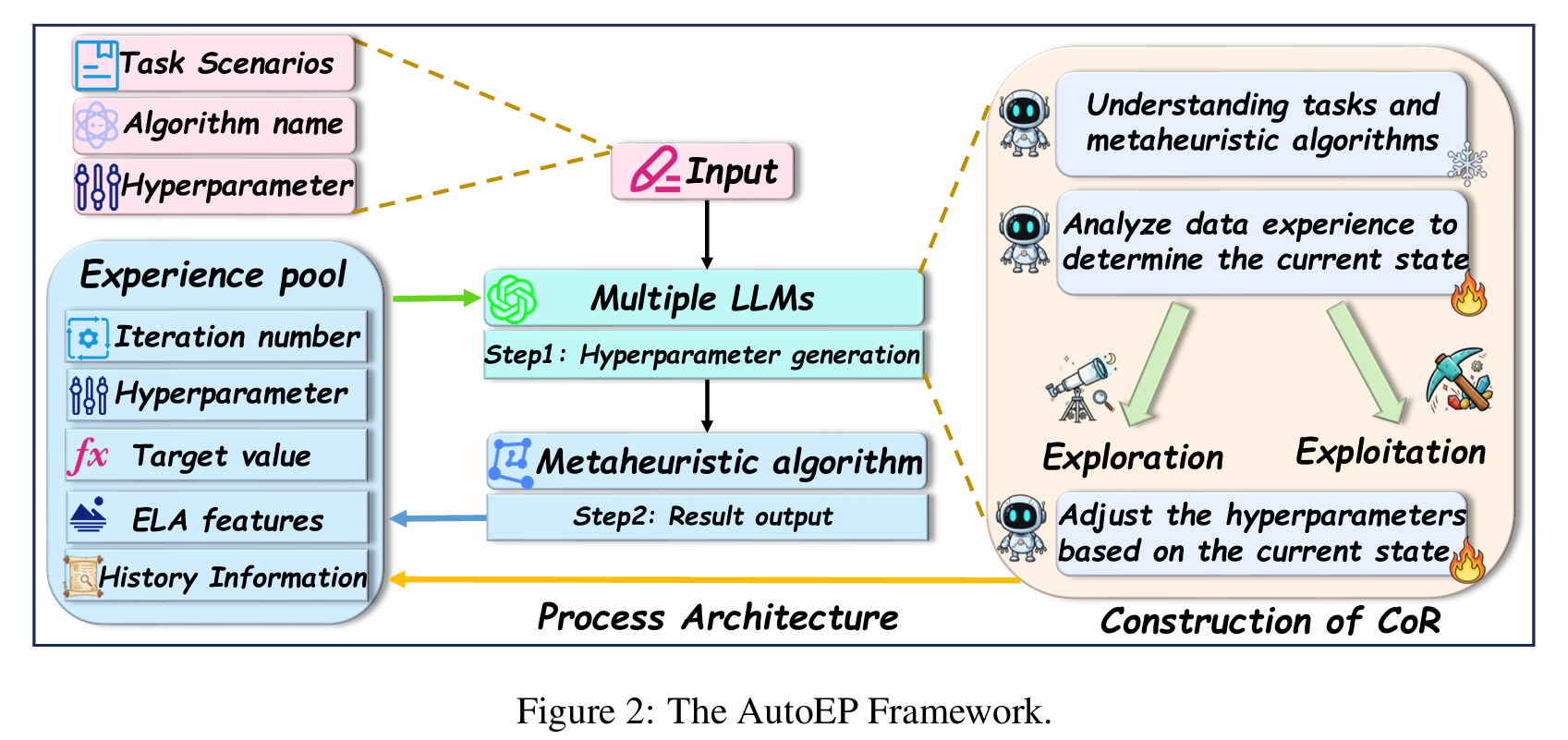
- ELA(Exploratory Landscape Analysis):
- 实时提取搜索状态特征(如种群分布、多样性、地形结构等);
- 将“黑箱”算法状态转化为结构化、可解释的数据。
- CoR(Chain of Reasoning)多 LLM 协作链:
- 将控制任务分解为三个子任务:
- Strategist:制定参数作用语义(如“突变率提升探索”);
- Analyst:基于 ELA 特征判断当前应“探索”还是“利用”;
- Actuator:生成具体的超参数值;
- 使用多个小型开源模型(如 Qwen3-30B)协作,避免依赖单一大型模型。
- 将控制任务分解为三个子任务:
- Experience Pool(经验池):
- 存储历史状态、参数与结果;
- 支持 LLM 进行上下文学习,提升调节策略的适应性。
方法
用定量搜索动态信息接地推理
为了有效控制元启发式算法,决策智能体必须对搜索过程有实时且定量的理解。由于元启发式算法本质上是黑箱,我们采用 探索性景观分析(Exploratory Landscape Analysis, ELA) 提取能够刻画算法状态的特征。我们精选了一组简洁但全面的特征,旨在捕捉搜索的四个关键方面:
- 当前种群适应度的统计分布;
- 局部适应度景观的结构特性;
- 解的多样性;
- 搜索的近期进展。
适应度分布特征
- 偏度(Skewness, $S$)
衡量当前种群内解分布的不对称性:
\[S = \frac{\frac{1}{n}\sum_{i=1}^{n}(y_i - \bar{y})^3}{\left(\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \bar{y})^2}\right)^3}\]- $y_i$:第 $i$ 个个体的适应度;
- $\bar{y}$:种群平均适应度;
- $n$:种群大小。
对于最小化问题:
- $S \approx 0$:分布对称,探索与利用平衡;
- $S > 0$:低质量解拖尾,应加强利用;
- $S < 0$:高质量解集中,有早熟收敛风险,应增强探索。
- 峰度(Kurtosis, $K$)
衡量适应度分布的尾部厚度:
\[K = \frac{\frac{1}{n}\sum_{i=1}^{n}(y_i - \bar{y})^4}{\left(\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \bar{y})^2}\right)^4} - 3\]- $K > 0$:解集中,多样性低,需增加探索;
- $K < 0$:解分散,需加强利用。
适应度景观与多样性特征
- 元模型决定系数($R^2$)
用简单模型(如二次函数)拟合样本解,评估景观的可预测性:
\[R^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - f(\mathbf{x}_i))^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2}\]- $f(\mathbf{x}_i)$:模型预测值;
- $R^2 \approx 1$:景观结构化(单漏斗),应加强利用;
- $R^2 \approx 0$:景观崎岖或多峰,应增强探索。
- 分散比(Dispersion Ratio, $D_{\text{ratio}}$)
比较最优 10%与最差 10%解的空间分布:
\[D_{\text{ratio}} = \frac{D(Q_{\text{best}})}{D(Q_{\text{worst}})}\]其中
\[D(Q) = \frac{2}{|Q|(|Q|-1)} \sum_{\substack{\mathbf{x}_i, \mathbf{x}_j \in Q \\ i < j}} d(\mathbf{x}_i, \mathbf{x}_j)\]- $d(\cdot,\cdot)$:决策空间距离(如汉明距离);
- $D_{\text{ratio}} \ll 1$(如 $<0.2$):最优解紧密聚集,单漏斗结构,应加强利用;
- $D_{\text{ratio}} \approx 1$:最优解分散,多峰景观,应增强探索。
搜索进展特征
- 变异性(Variability, $V$)
衡量最近 $m$ 代平均适应度的相对改善率:
\[V = \frac{\frac{1}{m}\sum_{g'=g-m}^{g-1} \bar{y}_{g'}}{\bar{y}_g}\]- $\bar{y}_g$:第 $g$ 代平均适应度;
- $V > 1$:足够进步,可加强利用;
- $V \leq 1$:停滞,需增强探索。
这些 ELA 特征将黑箱搜索状态转化为结构化、机器可读的表示,为 LLM 的推理过程提供实证基础,使其能够做出有依据的超参数调整决策。
LLM 驱动的闭环控制架构
AutoEP 作为一个闭环控制系统,迭代执行三大功能:
-
状态感知与上下文构建 每轮计算上述 ELA 特征,并与经验池(Experience Pool)中的历史状态、动作、结果拼接,构建结构化提示词。
-
多 LLM 推理链(CoR) 提示词送入 Chain-of-Reasoning 引擎,由多个协作 LLM 分析当前状态,决定探索或利用,并输出具体超参数配置。
-
动作与反馈 新配置送回元启发式算法,执行下一代搜索,并将结果存入经验池,完成反馈闭环,实现在线上下文学习。
用推理链分解控制逻辑
复杂控制任务涉及多维度推理:理解任务、诊断状态、决定动作。 若用单一 LLM 处理,会导致高延迟与输出不稳定。
为此,我们提出 Chain-of-Reasoning(CoR) 框架,将控制任务分解为三个专门化 LLM 代理:
| 代理 | 职责 | 触发频率 |
|---|---|---|
| Strategist | 生成静态控制映射(如“突变率↔探索”) | 仅运行前一次 |
| Analyst | 基于 ELA 特征与经验池,判断当前需探索 or 利用 | 每代一次 |
| Actuator | 根据 Analyst 指令与 Strategist 映射,输出具体数值 | 每代一次 |
Actuator 的两阶段决策
- 参数选择:依据控制映射,确定需调节的参数(如“提升突变率”);
- 幅度确定:参考经验池中相似状态下有效调整幅度,通过上下文学习决定步长。
这种分解式 CoR 流水线将非结构化控制问题转化为一系列聚焦、互联的推理任务,显著提升可靠性与效率,并降低对单一大模型的依赖。
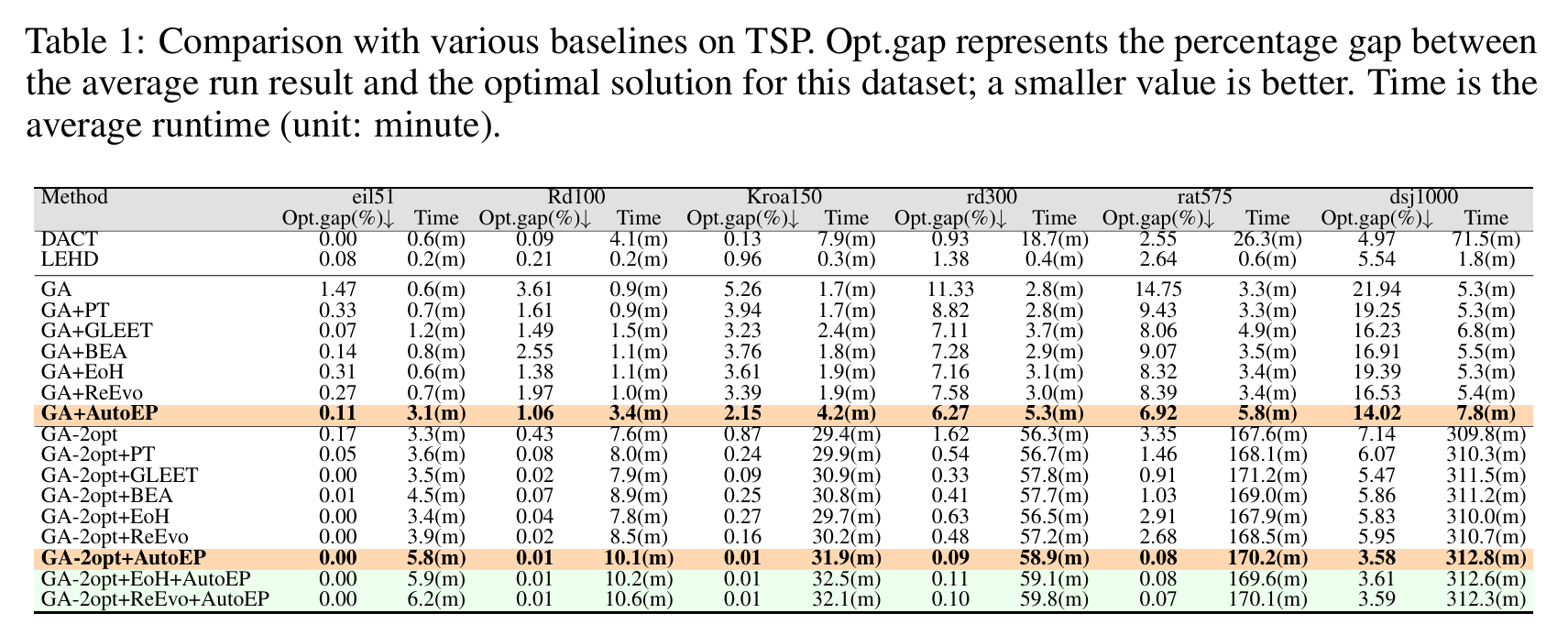
实验
审稿人意见
需要用户有一定的专业知识。
PaT: Planning-after-Trial for Efficient Code Generation
https://openreview.net/forum?id=767aZTpsIl
韩国浦项科技大学
rating:6422,withdraw
研究对象
旨在解决大语言模型(LLM)在代码生成任务中面临的高推理成本和效率问题。
痛点
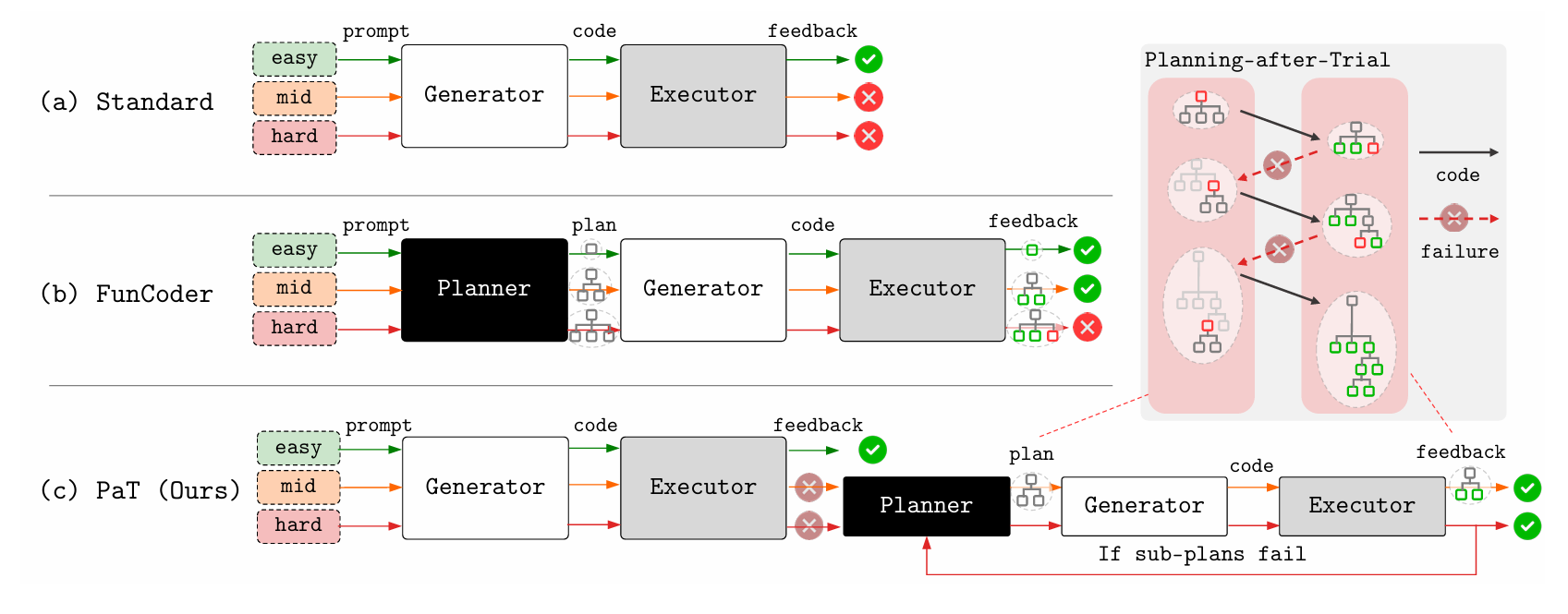
现有方法普遍采用先规划后尝试(Planning-before-Trial, PbT)的策略:在任何求解尝试之前,就一次性生成完整分解计划。如图所示,这种预先规划存在根本低效性:
- 对可直接求解的简单问题,仍强制支付分解开销;
- 分解计划未考虑生成模型的真实能力,可能产生依旧难以实现的子问题。
因此,PbT 策略常在简单任务上浪费资源,在复杂任务上又力不从心。
方案
为在简单问题上保持高效、在复杂问题上保持有效,我们提出先尝试后规划(Planning-after-Trial, PaT)的自适应策略,把刚性 PbT 彻底“反转”:
- 先由生成器直接输出完整代码并执行验证;
- 仅当验证失败时,才调用规划器进行问题分解。
PaT 用“直接尝试”的反馈作为信号,只在被证明需要时才触发规划。PaT 在显著提升通过率的同时,大幅降低了平均计算成本,将成本-性能帕累托前沿向前推进。其效率来源于“简单问题便宜处理,困难问题集中火力”。
PaT 的效率在异构模型配置中进一步放大。该配置把“生成”与“规划”两种角色分离:
- 生成器(Generator):处理高频、规模可控的子问题,可用成本极低的小模型(sLM);
- 规划器(Planner):处理低频但复杂的分解任务,需能力强劲的大模型(LLM)。
审稿人意见
有相同的工作,论文中的数学推导像是装饰。
LLM-First Search: Self-Guided Exploration of the Solution Space
https://openreview.net/forum?id=97kU2E3UKU
rating:226, Reject
伦敦大学学院
背景
大型语言模型(LLM)的推理与规划能力已通过“增加测试阶段算力”得到显著提升,这一过程类似于人类的“系统 2”思维——缓慢而审慎,而非快速、直觉的“系统 1”思维。早期的提示技术,如CoT启发了基本的系统 2 推理,但近期工作开始将推理重新定义为搜索问题,借助MCTS等经典算法。MCTS 与 LLM 的结合已在多个领域被证明有效,并得到了广泛采用。这些系统通常集成 LLM 世界模型、奖励/价值估计器、自一致性、自我修正、多智能体辩论与记忆模块,以达到 SotA 结果。
MCTS 的一个关键局限是它对“探索-利用”权衡的敏感性,该权衡由探索常数 c 控制。尽管超参数调优可针对特定任务优化性能,但固定的 c 无法适应不同难度的问题或不同能力的 LLM,导致在某些场景下过于昂贵或不切实际。过度探索会妨碍 LLM 在简单任务上发挥先验优势,而探索不足又会限制其解决更难问题的成功率。这一长期存在的问题与近期大型推理模型的发现相似:它们可能因过度依赖系统 2 思维而在简单任务上“想太多”,类似于 MCTS 因 c 值过高而过度探索。
核心思想
把搜索过程的控制权完全交给大模型自己,让模型在“探索-评估-决策”每一步都用自己的语言推理能力来决定下一步怎么走,而不再依赖任何人工设计的启发式、超参数或经典搜索算法(如 MCTS 的 UCB 常数、Best-FS 的贪心价值、ToT-BFS 的固定束宽等)。
贡献
LLM-First Search(LFS),一种全新的 LLM 自引导搜索方法,它无需预定义搜索策略,而是赋予 LLM 自主控制搜索过程的权力。LFS 不再依赖外部启发式或硬编码策略,而是让模型基于其内部评分机制,自行判断是继续当前搜索路径还是探索其他分支。这使得推理更具灵活性,并对上下文敏感,而无需手动调优或针对任务的特定适配。实验表明,LFS
(1)在更难的任务上表现更佳,且无需额外调参;
(2)在计算效率上优于其他方法,尤其在更强模型上优势更明显;
(3)因“LLM 优先”设计,随模型能力提升而更好地扩展;
(4)随测试阶段算力预算增加而更好地扩展。
方法
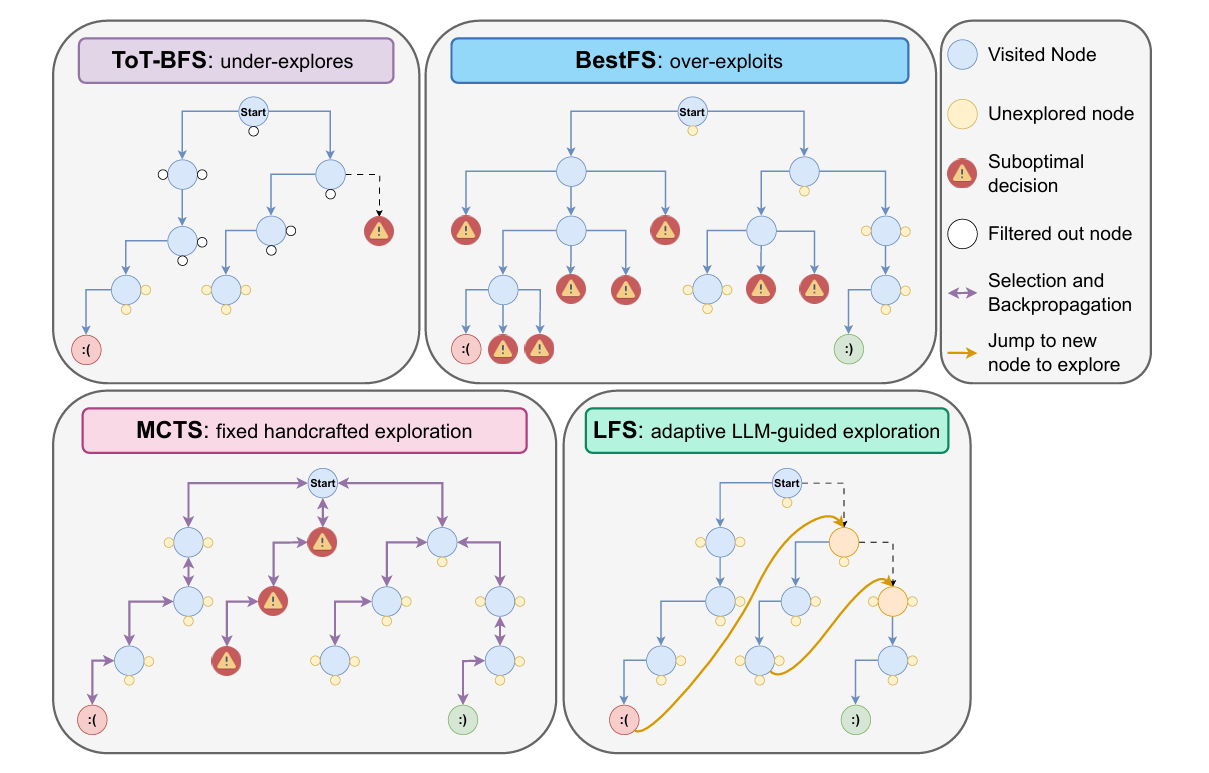
省流:把“搜索控制权”内化为 LLM 的语言推理步骤,让模型用自然语言自问自答: “当前路径有希望吗?”、“要不要换条支线?”——从而一次性扔掉所有人工超参数,实现任务无关、模型无关、无需调参的自适应搜索。
审稿人意见
创新有限。(这篇论文加上附录有61页,但方法部分只有半页)
ARS: Automatic Routing Solver with Large Language Models
https://openreview.net/forum?id=Tw1kyA5akb
rating:4444, Reject
zhenkun wang、qingfu zhang和fei liu课题组
背景
车辆路径问题(VRP)是组合优化中的经典难题,广泛应用于物流、配送、制造等领域。实际问题中往往包含多种复杂约束(如容量限制、时间窗、取送货、优先级等),导致:
- 手工设计启发式算法耗时耗力;
- 现有方法只能处理少数标准VRP变种;
- 通用求解器(如OR-Tools、Gurobi)在建模复杂约束时效率低、易出错。
核心思想
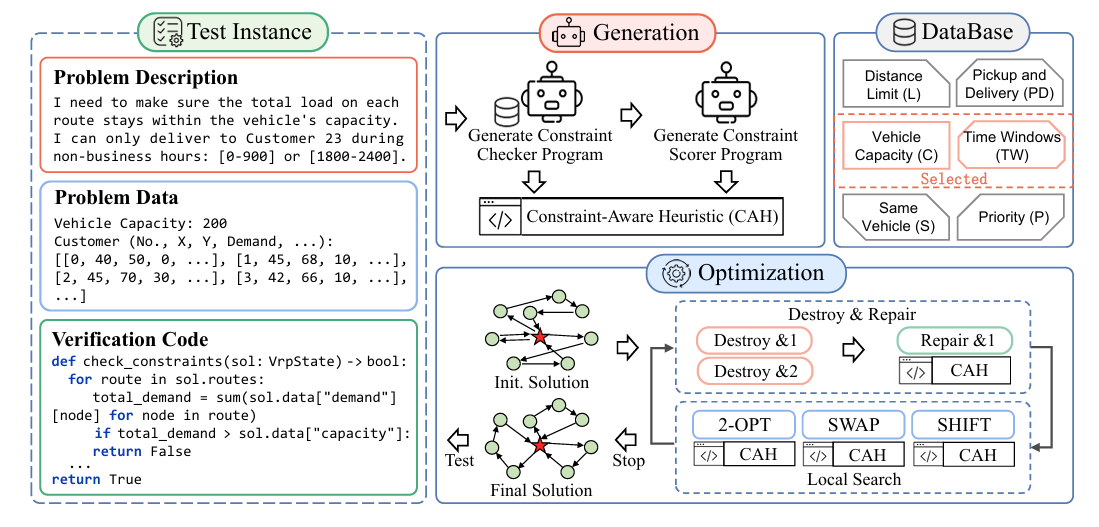
ARS 利用大语言模型(LLM)自动生成约束感知的启发式代码,嵌入到一个统一的元启发式求解框架中,实现对任意VRP变种的自动求解。其核心组成包括:
- 预定义约束数据库(Database) 包含6类典型约束(容量、距离、时间窗、取送货、同车、优先级)的描述与可行性检查代码。
- 约束感知启发式生成模块(CAH)
- 约束选择:基于RAG从数据库中检索相关约束;
- 约束检查器生成:LLM根据问题描述生成可行性判断函数;
- 约束评分器生成:LLM生成衡量约束违反程度的评分函数;
- 启发式策略集成:将上述函数嵌入到破坏-修复与局部搜索过程中,指导求解。
- 增强型启发式求解器(Augmented Heuristic Solver) 使用破坏-修复(Destroy & Repair)与局部搜索(2-opt、Swap、Shift)等操作,结合CAH策略进行迭代优化。
实验
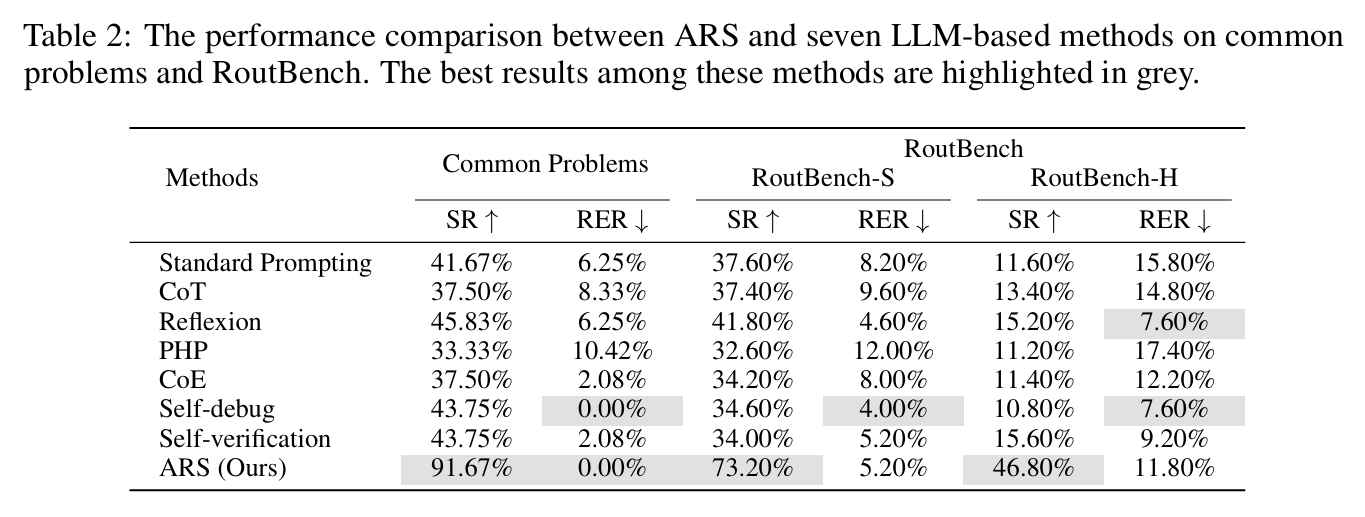
成功率(SR)衡量生成的解决方案通过验证过程的程序比例。
Runtime Error Rate(RER)是由于不合时宜的错误、API使用不当或语法错误而失败的程序的百分比。
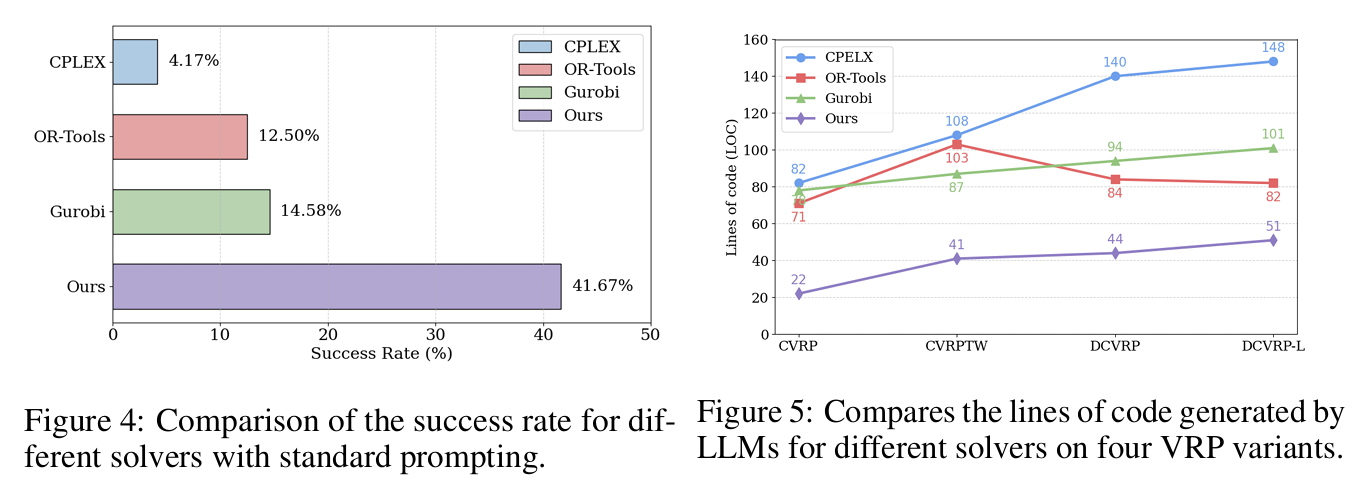
ARS 的成功率显著高于其他求解器,且生成代码行数最少,说明其框架更易于 LLM 理解与生成。
审稿人意见
现有技术的组合,创新性有限。
依赖搜索框架。
约束违反交给LLM判断,判断错了怎么办。
DHEvo: Data-Algorithm Based Heuristic Evolution for Generalizable MILP Solving
https://openreview.net/forum?id=VJLRgDLKwP
rating:4644, Reject
哈工大、华为诺亚方舟
背景
MILP 是组合优化、运筹学和计算机科学中的核心问题,广泛应用于供应链、硬件设计、生产调度、能源管理等领域。 Diving 启发式是一种在分支定界(B&B)框架下,通过迭代固定变量来快速寻找可行解的策略。
然而,现有方法存在两个主要问题:
- 人工设计启发式依赖专家经验,适应性差;
- 基于学习或 LLM 的方法往往只在训练实例上表现好,泛化能力差,因为同一类 MILP 问题内部结构差异很大。
核心思想
DHEvo 不再将“实例”视为静态训练数据,而是将实例和算法一起演化:
- 每代演化中,选出“结构代表性高、算法表现好”的实例-算法对;
- 用这些“好对”继续生成新的算法和实例,逐步提升算法的泛化能力;
- 引入多智能体 LLM 系统(MA-Evolution System)来自动生成、评估、改进启发式代码。
方法
如图所示,框架采用结构化演化流程,将实例选择与启发式生成紧耦合:
- 初始化:从领域数据集中随机采样实例,利用基于 LLM 的多智能体演化系统(MA-Evolution System)为每个实例生成唯一“实例-启发式”对,形成初始种群。
- 评估与选择:在每对实例上评估对应启发式,按适应度(相对原始间隙)采用温度控制策略挑选高分对。通常,高适应度启发式对应的实例结构更简单。
- 迭代演化:保留的高分启发式将在下一代继续演化,低性能对被淘汰。生成-评估-选择-重初始化循环重复多代,使实例与启发式协同进化。
- 终止与输出:最终产生在实例层面表现优异、在整个问题类上泛化可靠的 diving 启发式。
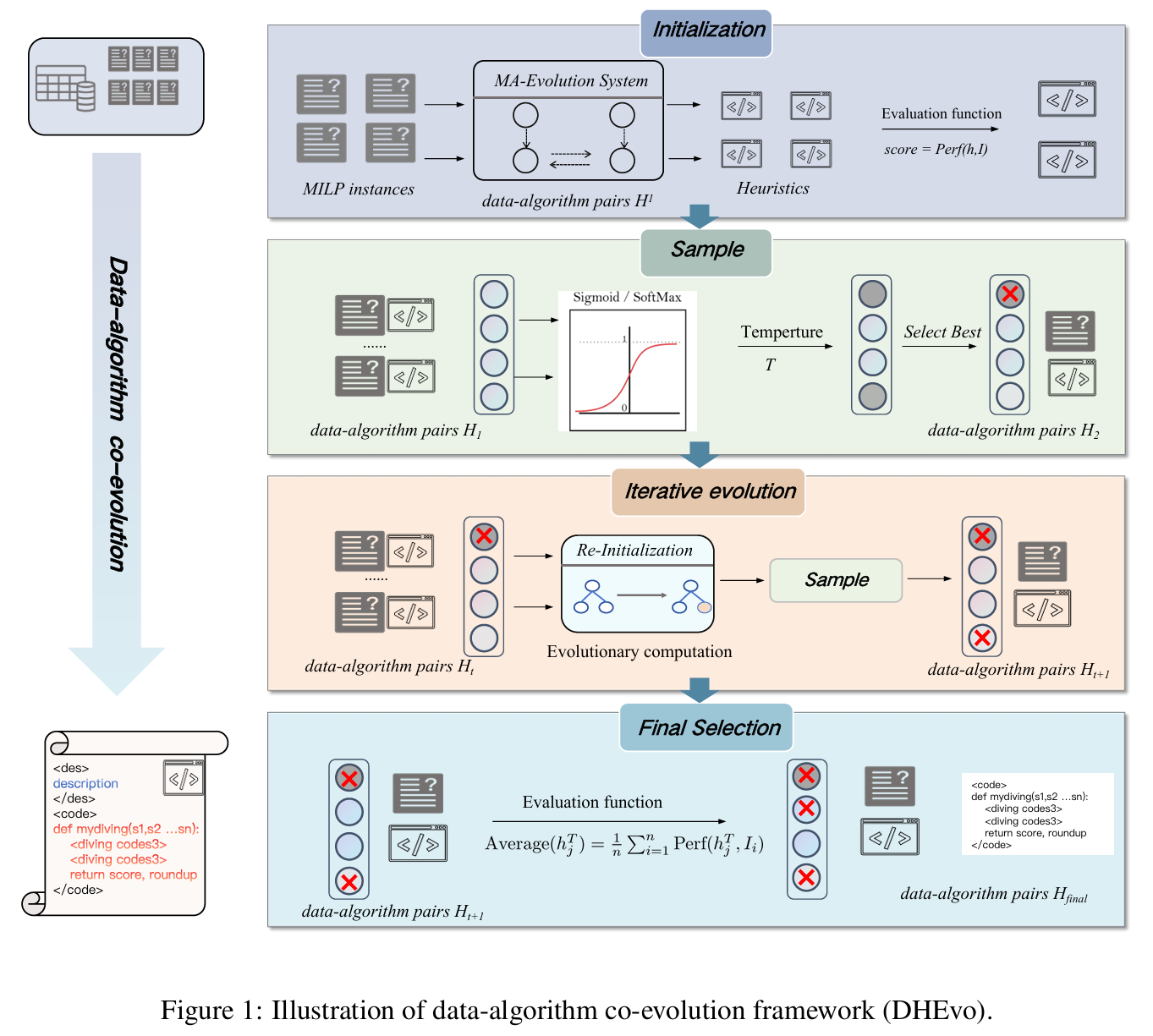
演化框架包含四大操作:初始化、交叉、变异、父代选择。通过精心设计的提示词(prompt)完成前三者;父代选择采用基于适应度的比例选择(fitness-proportional selection),平衡探索与利用。
MA-Evolution System
为生成高质量启发式,我们提出多智能体演化系统,受多智能体辩论启发,包含三阶段:
- Designer:接收 MILP 任务上下文、现有代码及演化操作类型,输出高层设计与步骤。
- Coder 与 Reviewer 循环:Coder 按设计生成代码;Reviewer 编译并逻辑分析,给出反馈;两者迭代改进。
- Judge:若循环未达成共识,Judge 综合历史交互做出最终裁决,输出代码与描述。
Prompt Engineering
提示设计遵循三条原则:
- 演化特异性对齐:显式嵌入演化操作语义;
- 角色专业化:明确 LLM 在 MA-E 中的职能;
- 问题上下文化:引入 MILP 与 diving 背景知识。
实验
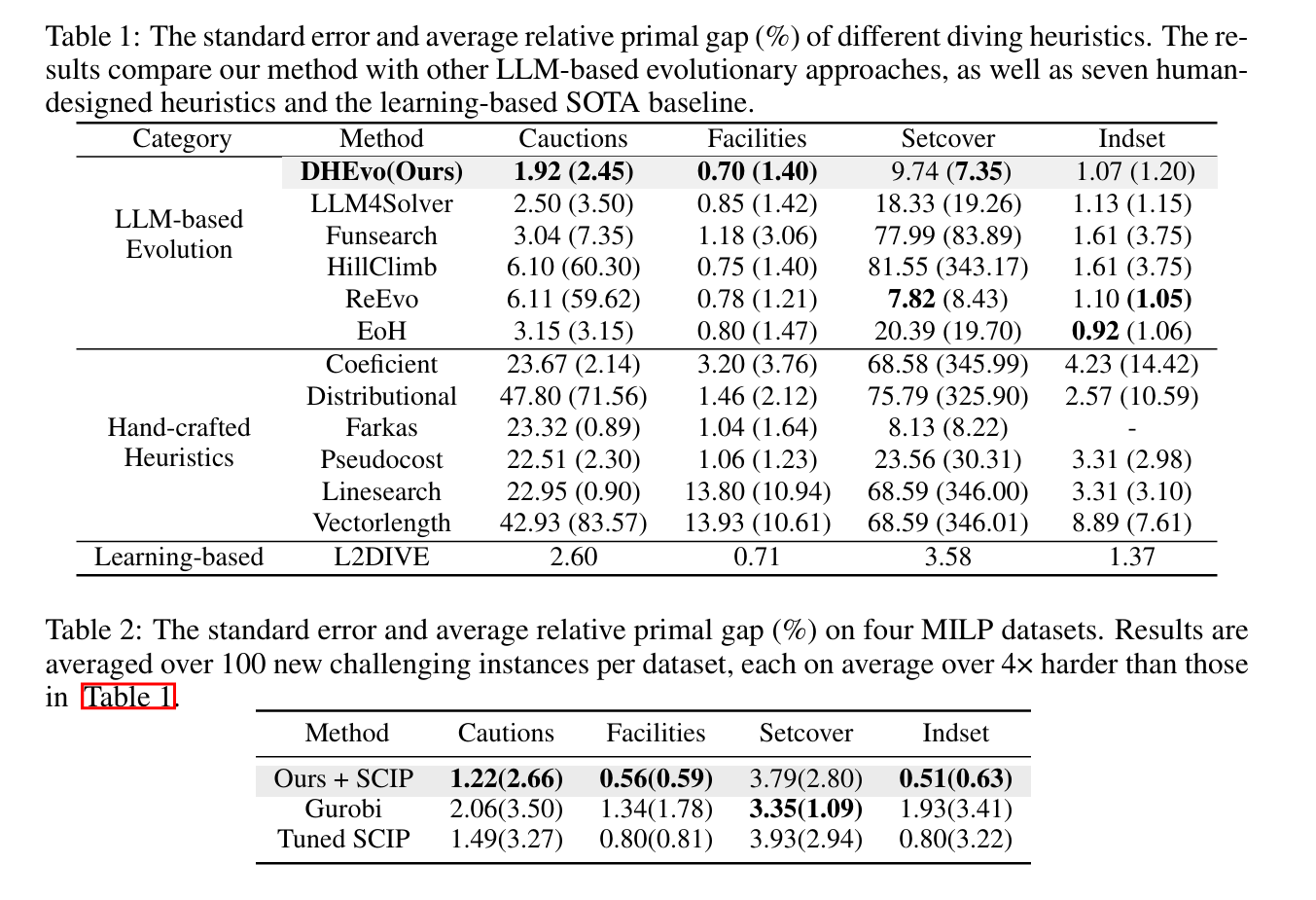
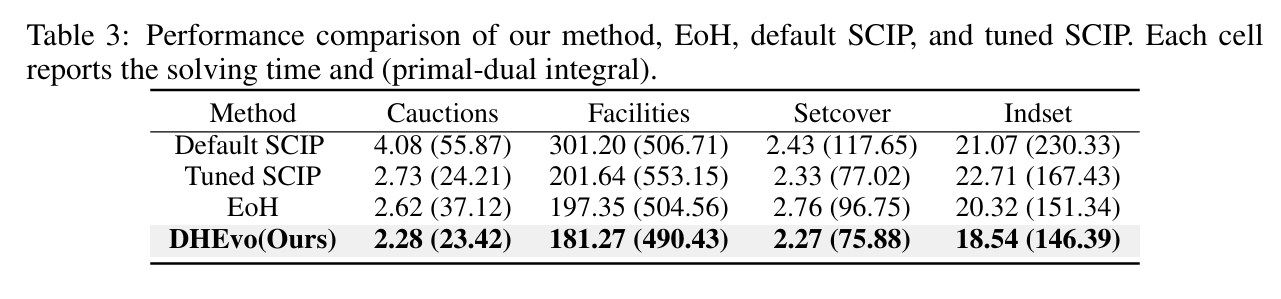
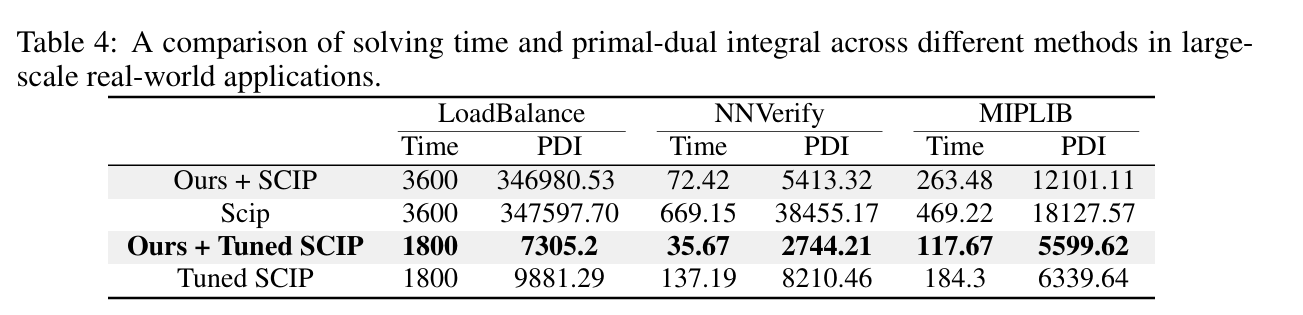
审稿人意见
比较温和。
回复澄清,LLM并不演化实例,而是作为输入提供。
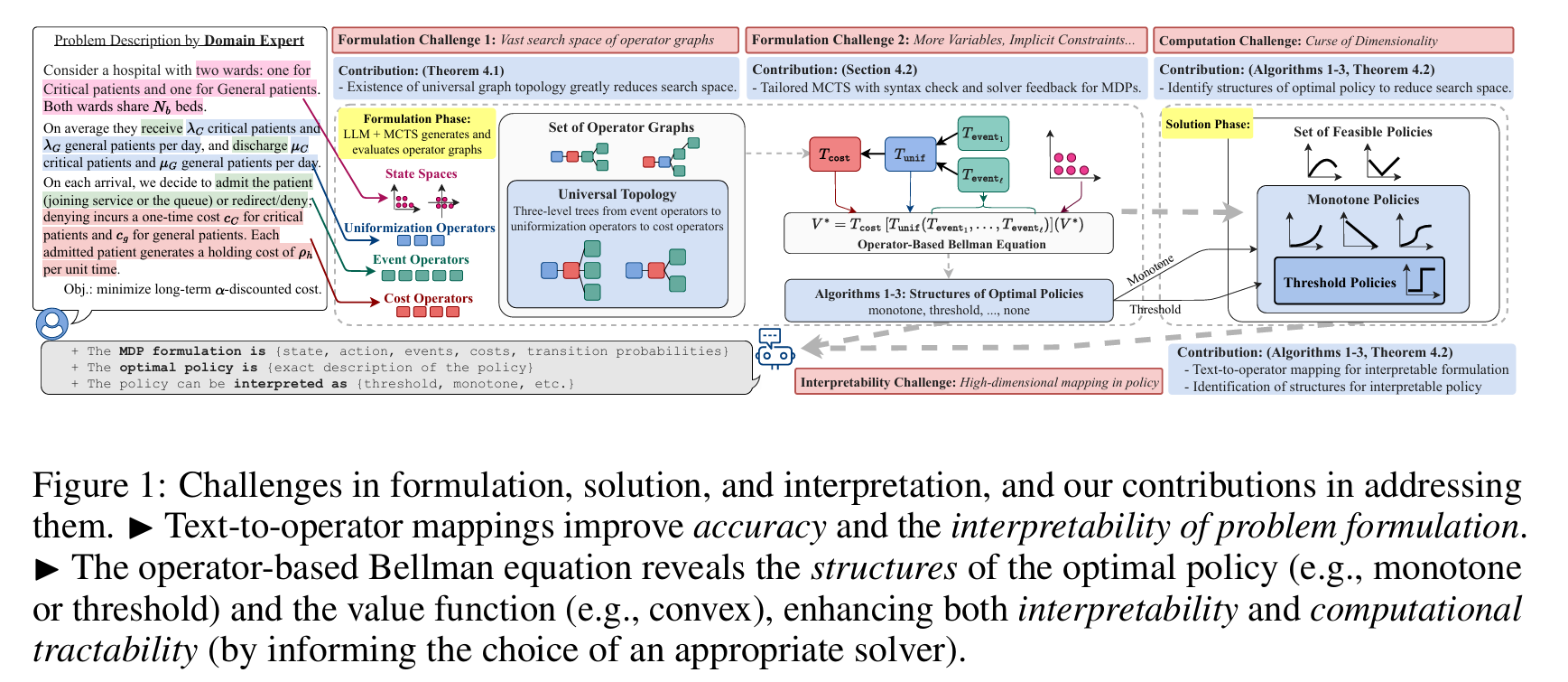
Operator Theory-Driven Autoformulation of MDPs for Control of Queueing Systems
https://openreview.net/forum?id=hPOImB2mZW
rating:2 8 10 8, Accept
研究对象
如何使用大语言模型(LLM)自动将自然语言描述的排队系统控制问题,转化为马尔可夫决策过程(MDP)的数学形式,并进一步识别最优策略的结构性质(如阈值策略、单调性等),从而加速求解并提升可解释性。
痛点
挑战一:建模难度
与一次性优化问题不同,MDP 需要:
- 明确状态空间(state space);
- 定义动作空间(action space),且可能依赖于状态;
- 推断转移概率(transition probabilities);
- 处理隐含约束(如队列长度非负);
- 建模事件驱动的随机动态(如到达、服务、转移)。
这些组件往往不会显式出现在自然语言描述中,必须自动推断。
挑战二:计算复杂度
- 即使建模正确,MDP 仍面临维度灾难(curse of dimensionality);
- 若能在求解前识别最优策略的结构(如阈值策略、单调策略),则可大幅缩小搜索空间;
- 例如:若证明最优策略是阈值型,则只需搜索阈值而非所有策略。
挑战三:可解释性
- 优化问题的解是变量取值,易于理解;
- 而 MDP 的解是策略函数(policy function),映射状态到动作,高维、难解释;
- 若能识别策略的结构性质(如“当病人数 < 5 时接收”),则可提升可解释性。
解决方案
提出一个基于算子理论(operator theory)的自动建模框架,核心思想是:
将 Bellman 方程表示为一个有向无环图(DAG),每个节点是一个算子(operator),对应某个事件(如到达、离开、转移)对值函数的可解释变换。
贡献
| 贡献维度 | 内容 |
|---|---|
| 理论 | 证明了一类事件驱动 MDP 的 Bellman 方程总可表示为三层算子图(Universal Topology) |
| 算法 | 提出基于 MCTS 的 LLM 建模方法,逐步构建算子图,结合语法检查与求解器反馈 |
| 结构识别 | 提出低复杂度算法,自动识别值函数的性质(如凸性、单调性),从而推断最优策略结构 |
| 实验 | 构建首个排队控制问题的自然语言数据集,36 个问题,83.3% 建模准确率,74% 结构识别率 |
例子
医院床位控制
自然语言: “医院有两个病房,共享床位。病人随机到达,医生决定是否接收。拒绝有惩罚,住院有持有成本。”
自动输出:
- 状态:$x = (x_C, x_G)$,表示两类病人数;
- 事件:到达、离开;
- 算子:
- 控制到达:$T_{\text{CA},C}(V)(x) = \min\lbrace V(x + e_C) + c_C, V(x)\rbrace $
- 非控制离开:$T_{\text{D},C}(V)(x) = V((x_C - 1)^+, x_G)$
- 结构识别:最优策略是阈值型,即:
当 $x_C + x_G \leq \theta$ 时接收病人。
方法
框架分为两个步骤:
- 自动建模:从自然语言描述中自动构建基于算子的 Bellman 方程(即算子图);
- 结构识别:从算子图中自动识别最优策略的结构性质(如阈值、单调性等)。
理论基础:算子图的通用拓扑结构
将 Bellman 方程视为一个有向无环图(DAG),其中:
- 每个节点是一个算子(operator),表示对值函数的某种变换;
- 边表示算子之间的依赖关系;
- 输入是 $V_n^\ast(x)$,输出是 $V_{n+1}^\ast(x)$。
关键问题:搜索空间巨大
-
若有 $N$ 个算子,可能的 DAG 数量为:
\[\text{Number of DAGs} \sim 2^{N^2}\]例如,$N=9$ 时,数量级为 $10^{11}$。
理论贡献(定理 4.1)
\[V_{n+1}^*(x) = T_{\text{cost}} \left\lbrace T_{\text{unif}} \left( T_{e_1}[V_n^*(x)],\ T_{e_2}[V_n^*(x)],\ \dots,\ T_{e_\ell}[V_n^*(x)] \right) \right\rbrace\]定理 4.1(通用拓扑结构) 对于任意事件驱动 MDP,其 Bellman 方程可表示为以下三层算子图:
其中:
- $T_{\text{cost}}[U(x)] = c(x) + \gamma \cdot U(x)$
- $T_{\text{unif}}[U_1,\dots,U_\ell] = \sum_{j=1}^\ell P(e_j \mid x) \cdot U_j(x)$
- $T_{e_j}[V_n^*(x)] = V_{n+1}(x, e_j)$:事件 $e_j$ 对应的算子
结论:我们不再需要搜索所有可能的 DAG,只需搜索三层结构,且每层算子类型固定。
基于 MCTS 的自动建模算法
使用蒙特卡洛树搜索(MCTS)引导 LLM 逐步构建算子图。
搜索树结构(4 层)
| 层级 | 名称 | 内容 |
|---|---|---|
| m1 | 参数层 | 定义问题参数(如到达率、服务率、床位数) |
| m2 | 状态层 | 定义状态变量与约束(如队列长度非负) |
| m3 | 事件层 | 定义事件、概率、动作、成本 |
| m4 | 算子层 | 为每个事件选择对应的算子(如 $T_{\text{CA}}, T_{\text{D}}, T_{\text{TD}}$) |
MCTS 四步循环
- 选择(Selection)
- 使用 UCT 公式选择子节点:
- 扩展(Expansion)
- 用 LLM 生成候选子节点(如事件、算子);
- 检查语法一致性(如概率和是否为1);
- 若不一致,允许最多5次重试,否则终止并回传奖励0。
- 评估(Evaluation)
- 对中间节点:用 LLM 自评生成质量,给出初始分数;
- 对终端节点:用求解器验证是否能收敛;
- 最终奖励:
- 回传(Backpropagation)
- 从叶节点向上更新每个节点的值与访问次数:
自动结构识别算法
目标:
给定一个算子图,自动识别值函数的性质(如凸性、单调性),从而推断最优策略的结构(如阈值策略)。
核心思想:
- 每个算子 $T$ 会传播某些性质;
- 若所有算子都传播某个性质,则整个 Bellman 方程也传播该性质;
- 最终值函数 $V^*$ 必具有该性质,从而可推断策略结构。
示例:
- 若 $V^*$ 是凸函数,则最优策略是阈值型;
- 若 $V^*$ 是单调递增,则最优策略是单调递减。
难点:
- 每个算子可能传播多个性质;
- 性质之间存在包含关系(如 $\text{Super} \cap \text{SuperC} \subset \text{Cx}$);
- 暴力枚举所有性质的交集是指数复杂度。
算法:
- 使用动态规划高效寻找所有算子共同传播的最小性质空间;
- 时间复杂度:$\mathcal{O}(N \mid \mathcal{G}\mid ^2)$;
- 空间复杂度:$\mathcal{O}(N \mid \mathcal{G}\mid )$;
- 其中 $N$ 是性质数量,$\mid \mathcal{G}\mid $ 是算子数量。
定理 4.2(结构识别保证) 给定算子图 $\mathcal{G}$,算法1–3可自动识别出所有可传播的结构性质,且复杂度为多项式时间。
审稿人意见
2分的说有先前的相关工作。
Large Language Model Guided Dynamic Branching Rule Scheduling in Branch-and-Bound
https://openreview.net/forum?id=8LCdjf7uIk
rating:444, Reject
研究对象
分支定界算法。
痛点
- 分支规则对求解速度影响巨大,但传统 solver 通常固定一条规则跑到底。
- 人工/专家规则切换需要深厚领域知识,跨问题类型泛化差。
- 现有学习方法要采集大量数据、训练专用网络,成本高且易过拟合。
方法
省流:给 LLM 自主权,根据问题类型和搜索树状态切换分支规则,无需训练就解决MILP 实例。
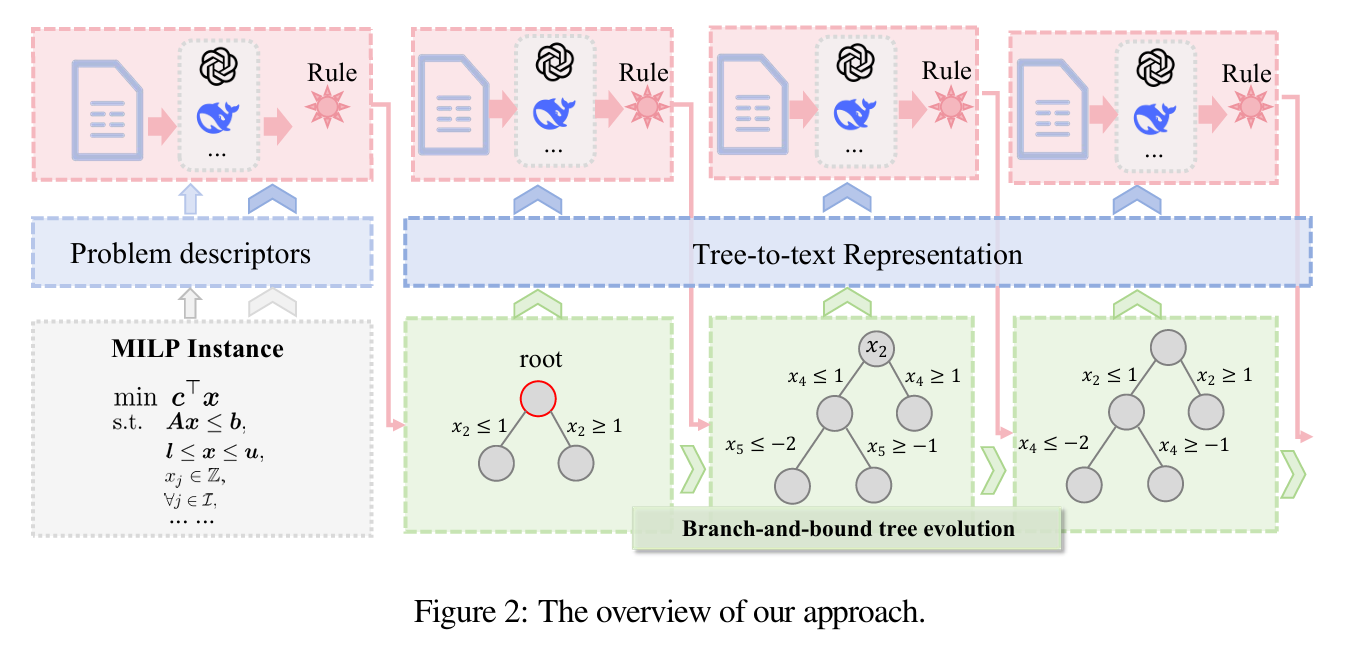
提出一种由大语言模型驱动的动态分支规则调度方法,以增强分支定界(B&B)算法。如图所示,框架分为三步:
- 初始化阶段:LLM 根据问题类型与规模推荐初始分支规则;
- 求解阶段:将不断演化的搜索子树转化为文本描述,LLM 据此决定是否切换规则;
- 效率与鲁棒性:多 LLM 异步并行推理,投票产生最终决策,避免阻塞求解器。
初始分支规则
为整个 B&B 搜索选定一条合适的起步规则至关重要。不同规则的性能高度依赖于问题类型(例如 set covering、maximum independent set 等)与规模(变量数、约束数)。传统做法依赖专家经验人工指定。我们利用 LLM 中蕴含的广泛先验知识,替代人工完成这一选择。
令 $\mathcal{R}=\lbrace r_1,\dots ,r_M\rbrace $ 为候选分支规则集合。对给定 MILP 实例 $\mathcal{P}$,提取两类高层描述:
- 问题类型 $t$(可由用户指定,也可通过简单关键词匹配自动识别);
- 问题规模 $s\in\mathbb{R}^+$(变量数、约束数、非零密度等统计量)。
我们将上述信息编码为提示,调用一组 LLM:
\[\Pi=\lbrace \pi_1,\dots,\pi_M\rbrace , \quad \pi_i\bigl(\text{Prompt}(t,s,\mathcal{R})\bigr)\mapsto r_i,\]提示内还包含每条规则的启发式使用指南(摘自 SCIP 文档或文献),供 LLM 参考。最终规则由多数投票决定:
\[r^*=\mathrm{Vote}\bigl(\lbrace r_1,\dots,r_M\rbrace \bigr).\]该集成机制削弱单个模型幻觉的影响,提升初始推荐的鲁棒性。
动态规则切换
B&B 搜索树的结构随求解动态变化,全程沿用同一条规则往往次优。在合适时机切换到另一条规则可显著减少分支步数。我们设计了一种基于树状态文本化的在线切换机制。
树→文本表示
在当前第 $k$ 次分支时,我们维护一个长度为 $L$ 的队列:
\[\mathcal{T}_k^L=\lbrace v_{k-L+1},\dots ,v_k\rbrace ,\]记录最近 $L$ 个已探索节点及其六维指标:
Depth:节点深度Nodes:已探节点总数Gap:相对最优性间隙Cut:截止(cutoff)比例Dom:域缩减强度Cands:当前分支候选变量数H:候选变量熵
每次触发评估时,将队列中信息按固定模板转成一段自然语言描述 $\text{text}(\mathcal{T}_k^L)$。
切换指令
将 $\text{text}(\mathcal{T}_k^L)$ 作为上下文,再附上决策细则:
- 若滑动窗口内 $\Delta\mathrm{Gap}$ 持续下降、单节点改进率 $r>10^{-5}$,则保持当前规则;
- 若出现停滞(gap 几乎不变、cut/dom 指标恶化、熵过高或过低),则考虑切换;
- 根据当前深度、候选数、熵水平等,映射到最合适的替代规则(如深度 $\le 3$ 且候选 $\ge 50$ 优先选
fullstrong;深度 $\ge 15$ 避免昂贵规则,选relpscost或pscost等)。
LLM 输出所需切换的目标规则名称,仍采用多模型投票决定最终选择。整个查询过程异步执行, solver 不等答复,继续用最近一次生效的规则探索;待投票结果返回后,下一节点立即启用新规则。
异步多 LLM 决策机制
LLM 推理存在延迟与幻觉风险,直接阻塞求解器会严重拖慢整体效率。为此我们设计异步并行+投票机制:
异步监控
- 求解器把最新 $\text{text}(\mathcal{T}_k^L)$ 推送给后台 LLM 进程后立即返回,继续搜索;
- 多个 LLM 并行推理;
- 一旦投票结果就绪,调度器在下一节点生效新规则。
由于 B&B 步数通常很多,延迟若干步再做切换仍具备指导价值。
投票方案
设 $M$ 个 LLM 返回的规则集合为 $\lbrace r_1,\dots,r_M\rbrace $,最终决策
\[r^*=\mathrm{Vote}\bigl(\lbrace r_1,\dots,r_M\rbrace \bigr)= \mathop{\arg\max}_{r\in\mathcal{R}} \sum_{i=1}^M \mathbb{I}[r_i=r].\]仅当同一规则获得最多支持时才被采纳,从而过滤个别模型的异常或幻觉输出。
该设计同时缓解延迟与幻觉问题,使 LLM 的高层次知识能够安全、高效地嵌入 MILP 求解器。
实验
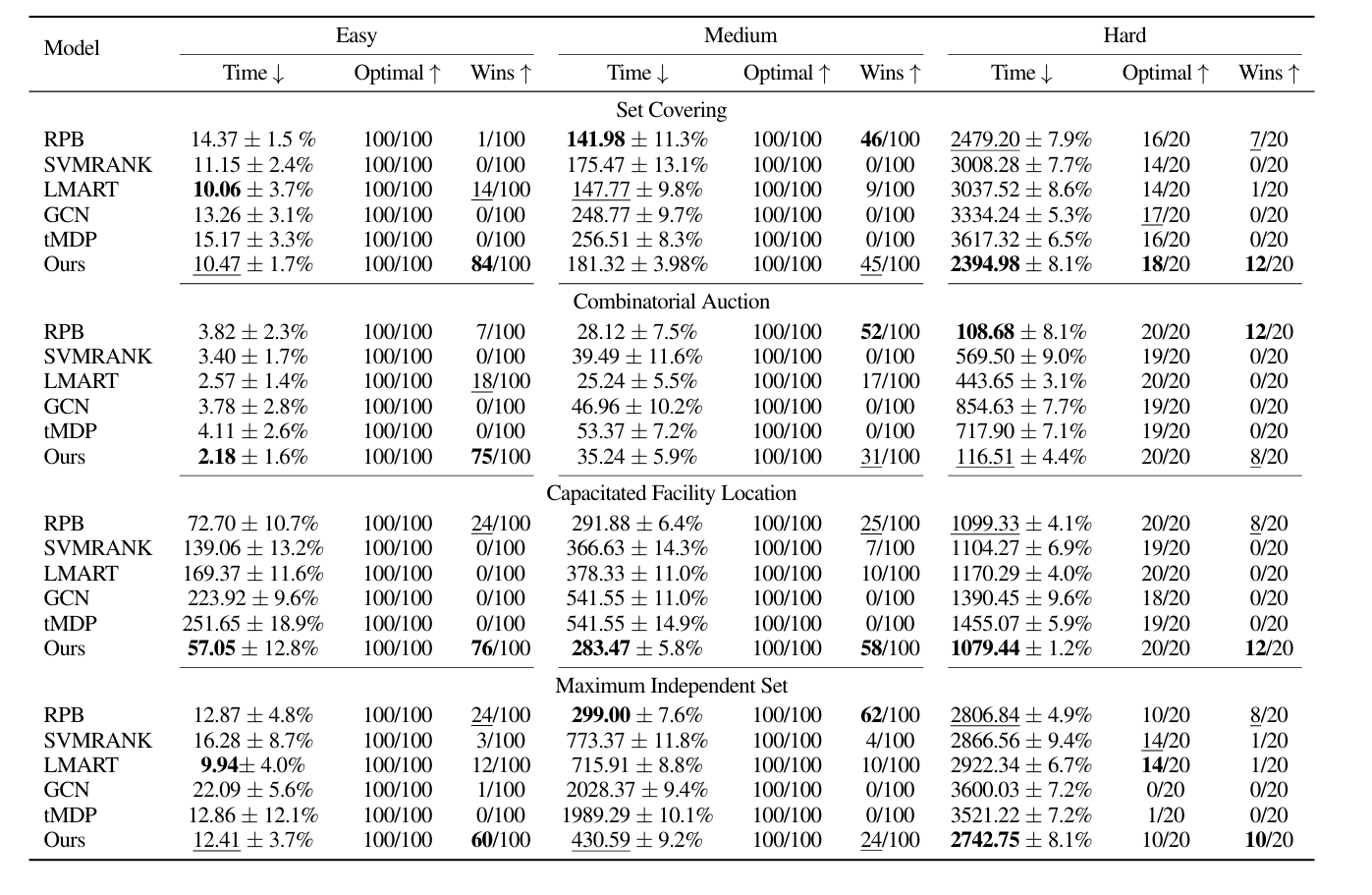
审稿人意见
实验比较不公平;需要大量手工prompt;没有和商业求解器耦合;没有理论保证;开销很大;扩展性不好。
HSRL: Hierarchical Spatial Reasoning with Large Language Model
https://openreview.net/forum?id=jJlB5blcNV
rating:2464,withdraw
港科大
痛点
尽管 LLM 在语言理解和抽象推理方面表现出色,但它们在空间推理方面表现较差,难以处理复杂的空间关系、路径规划和连续动作推理任务。这对它们在具身智能(embodied AI)等实际应用中的部署构成了严重限制。

贡献
- 提出 HSRL 框架:层次化空间推理方法
- 状态层次分解(State-Level Decomposition):让 LLM 自动生成关键中间状态(sub-goals),将复杂任务拆解为多个子任务。
- 环境层次分解(Environment-Level Decomposition):为每个子任务构建一个局部子环境,只保留相关信息(如障碍物),减少干扰,提升效率。
- 如果子任务无法解决,系统会动态扩展子任务范围,直到找到可行解。
- 提出 M-GRPO 算法:优化高层规划器
- 将 蒙特卡洛树搜索(MCTS) 与 GRPO(Group Relative Policy Optimization) 结合,用于在线微调 LLM。
- 引入细粒度的优势函数(fine-grained advantage function),在训练中对每个中间状态进行精确评估,解决传统方法中信用分配不清的问题。
- 通过 MCTS 探索多种路径候选,提升规划质量和多样性。
方法
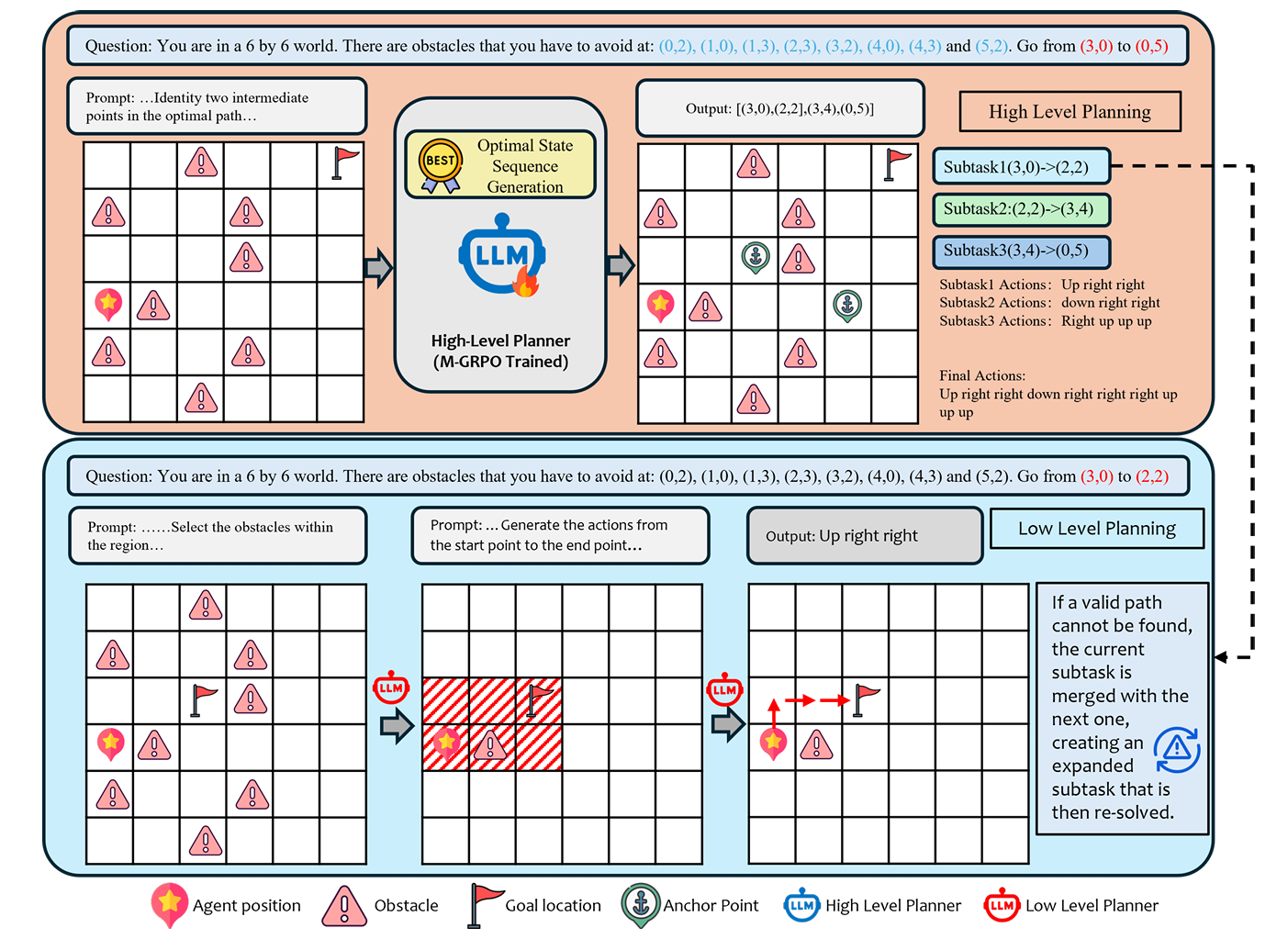
提出 HSRL 框架,以克服现有基于 LLM 的规划方法在复杂空间任务中的局限。该方法包含两个关键组件:
- 一种新颖的两级层次化框架,将复杂任务分解为一系列可管理的子问题;
- 一种创新的MCTS 引导微调方法 M-GRPO,用于提升生成规划的最优性。
基于状态与环境分解的层次化规划
我们的框架采用两级层次化分解策略,在状态层级和环境层级同时拆解复杂规划任务,从而有效降低问题复杂度。
状态层级分解
先前工作通过人工设定子目标将路径任务分段。我们拓展该思想,让 LLM 自动生成关键中间状态。给定任务的初始状态与目标状态,我们提示 LLM 推理并生成一条简洁的关键中间状态序列,从而将高层目标转化为一系列“状态→状态”转移,显著简化后续规划范围。
环境层级分解与动态扩展
在状态层级分解之后,大量全局环境信息对于当前子任务而言属于无关噪声,可能干扰推理。因此,在生成状态序列后,我们为每一对相邻中间状态定义一个子任务,并构建对应的局部环境——仅保留与该子问题相关的信息(如局部障碍物或地标)。这种层次化表示使模型聚焦于更小、更易管理的子环境,提升效率并缩小搜索空间。
若模型在局部环境中无法找到可行路径,则扩展子任务范围:将子任务的终点延伸至序列中的下一个中间状态,形成更大的子任务并重新求解。该过程可递归进行,直到找到解,或在最坏情况下回退至原始完整任务,确保对问题空间的稳健覆盖。
用 M-GRPO 优化规划
由于 LLM 在预训练阶段缺乏空间推理经验,其生成的中间状态序列往往次优。而中间状态的质量直接决定后续环境分解与底层动作规划能否成功。为此,我们提出一种在线学习方法,将 MCTS 的探索能力与 GRPO 的微调机制相结合,使 LLM 在探索过程中持续改进规划策略。
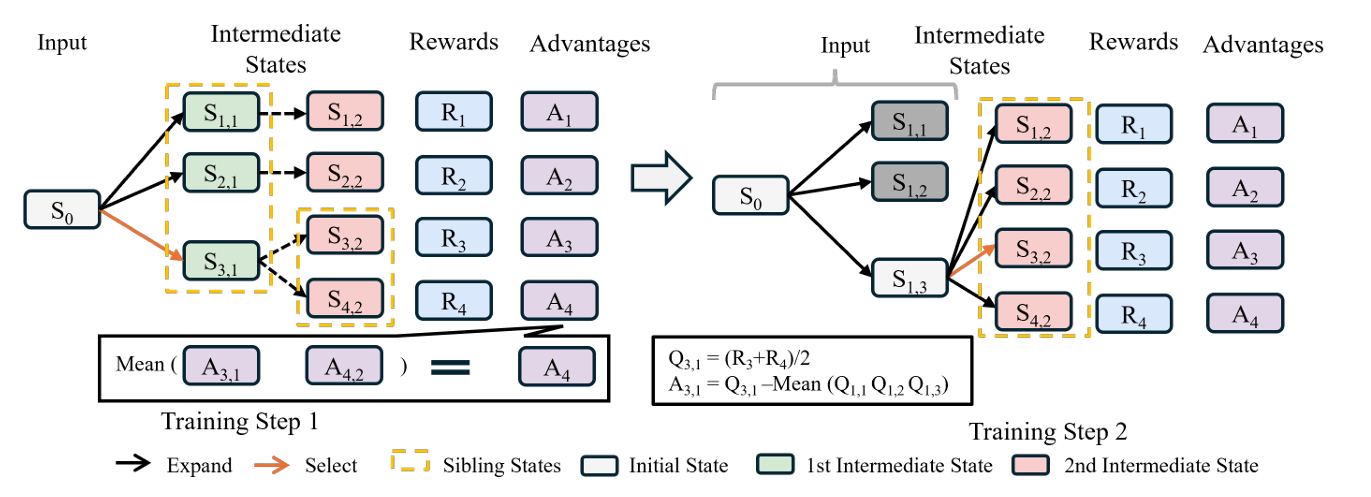
MCTS 引导的探索
我们将状态生成过程建模为搜索问题,由 MCTS 导航。搜索树中:
- 每个节点代表一个中间状态;
- 一条完整节点序列构成一条轨迹(称为 completion)。
算法从初始状态开始迭代构建树:
- 每次迭代,MCTS 策略遍历树至叶节点;
- 从该状态提示 LLM 生成若干后续潜在状态(扩展);
- 评估奖励(模拟);
- 沿路径更新 Q 值(回溯)。
中间状态的选择采用 UCT 公式:
\[s_{\text{next}} = \arg\max_{s' \in \text{Children}(s)} \left( Q(s') + c \sqrt{\frac{\ln N(s)}{N(s')}} \right)\]其中
- $Q(s’)$:状态 $s’$ 的估计价值;
- $N(s)$, $N(s’)$:访问次数;
- $c$:探索常数。
细粒度优势函数
传统 GRPO 使用整条轨迹的累积回报计算优势函数,导致信用分配模糊,无法辨识单个中间状态的贡献。为此,我们提出中间状态级的细粒度优势函数。
设 LLM 为某规划问题生成 $M$ 条候选序列(completions):
\[\lbrace \tau_1, \dots, \tau_M\rbrace , \quad \tau_m = (s_{m,1}, s_{m,2}, \dots, s_{m,T_m})\]令 $s_{m,n}$ 表示第 $m$ 条序列的第 $n$ 个中间状态。其状态值(Q 值)由所有经过该状态的蒙特卡洛模拟回报平均得到:
\[Q_{m,n} = \frac{W_{m,n}}{N_{m,n}}\]其中
- $W_{m,n}$:经过 $s_{m,n}$ 的所有模拟的累积奖励之和;
- $N_{m,n}$:访问计数。
我们定义状态 $s_{m,n}$ 的优势为其相对于兄弟状态(即共享相同前缀序列的其他候选状态 $\lbrace s_{j,n}\rbrace _{j=1}^M$)的相对表现:
\[A_{m,n} = Q_{m,n} - \operatorname{Mean}(Q_{\text{siblings}})\]该公式直接量化在某一决策点选择 $s_{m,n}$ 相较于平均替代方案的优劣。
注意:我们未对奖励进行归一化,以防止因高频生成最优路径而人为压低其价值(reward hacking)。
最后,为与 GRPO 框架对齐,我们将一条轨迹的所有中间状态优势取平均,得到该轨迹的整体优势:
\[A(\tau_m) = \frac{1}{T_m} \sum_{n=1}^{T_m} A_{m,n}\]该轨迹级优势 $A(\tau_m)$ 作为训练信号送入 GRPO 损失函数。这种细粒度优势计算使模型不仅能判断哪些完整序列有效,还能精确识别对构建最优规划最关键的中间状态。
M-GRPO 训练算法
| 步骤 | 内容 |
|---|---|
| 输入 | 高层规划器 $\pi_\theta$,初始状态 $s_0$,最大迭代次数 $N_{\max}$ |
| 输出 | 优化后的规划器 $\pi_\theta$ |
- $T \leftarrow \text{InitializeTree}(s_0)$
- $\text{iteration} \leftarrow 0$
- while $\text{iteration} < N_{\max}$ and not sufficiently deep do
- $L \leftarrow \text{SelectPromisingLeafNode}(T)$
- $\lbrace \tau_i\rbrace \leftarrow \text{ExpandAndSimulate}(\pi, L)$ // 生成新轨迹
- for each trajectory $\tau_m$ do
- $R_m \leftarrow \text{SimulateToGoal}(\tau_m)$ // 计算轨迹奖励
- $\text{Backpropagate}(T, \tau_m, R_m)$ // 更新 Q 值
- end for
- for each trajectory $\tau_m$ do
- $A_{\tau_m} \leftarrow [\ ]$ // 存储状态级优势
- for each state $s$ in $\tau_m$ do
- $p \leftarrow \text{GetParentNode}(s)$
- $Q \leftarrow \text{AverageQValue}(\text{siblings})$
- $A_s \leftarrow Q(s) - Q$ // 计算状态优势
- 将 $A_s$ 加入 $A_{\tau_m}$
- end for
- $A(\tau_m) \leftarrow \text{Average}(A_{\tau_m})$ // 轨迹级优势
- 将 $A(\tau_m)$ 加入 $A_{\text{all}}$
- end for
- $\pi_\theta \leftarrow \text{UpdatePolicy}(\pi_\theta, A_{\text{all}})$ // GRPO 更新
- $\text{iteration} \leftarrow \text{iteration} + 1$
- end while
实验
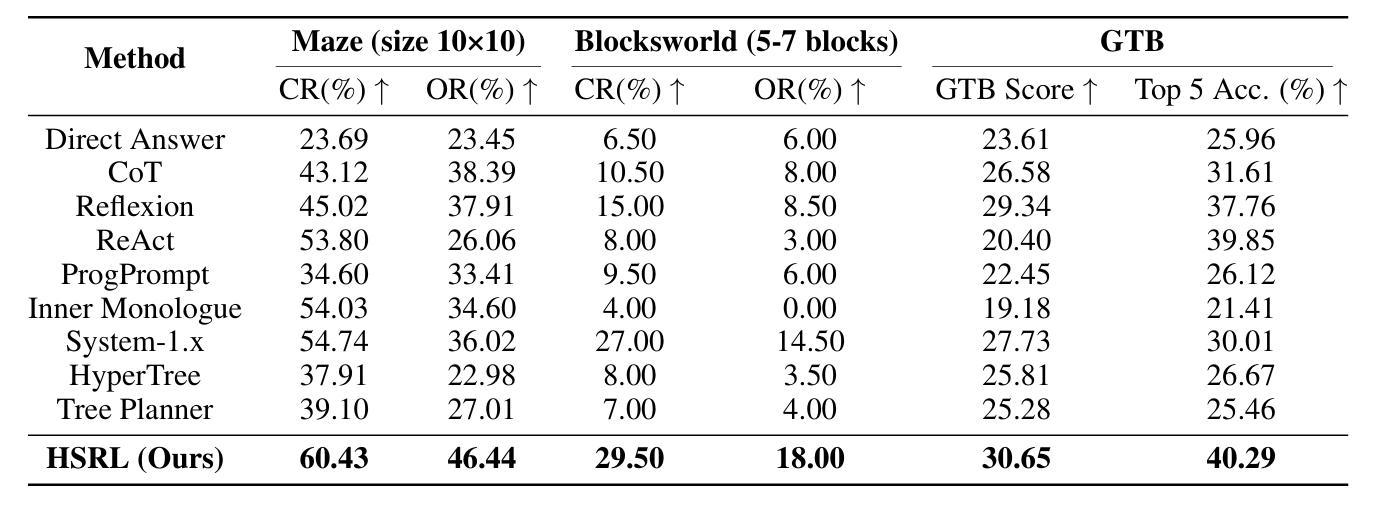
- CR(Completion Rate):任务完成率
- OR(Optimal Rate):路径最优率
- GTB Score:复杂地图下的综合评分
审稿人意见
文章没有提出新东西;写作不清晰;细节展示不足。