Chain-of-Context Learning: Dynamic Constraint Understanding for Multi-Task VRPs
Shuangchun Gui, Suyu Liu, Xuehe Wang, and Zhiguang Cao
ICLR2026,rating:44666
https://openreview.net/forum?id=AhE6aSlz5g
目标
痛点
- 启发式方法计算密集,通常需要大量手工设计的规则来适应不同的问题变体。
- 针对特定单一任务的神经VRP求解器由于大量但必要的重新训练或微调而效果较差。
- 统一框架的VRP求解器,在编码状态将信息静态编码,解码的时候整合动态信息。静态节点嵌入在解码步骤中保持固定,因此无法反映这种动态特性。虽然上下文被更新,但这种不对齐的上下文-节点对可能导致状态估计不准确,从而误判下一个决策。
关键挑战:
-
每个约束的重要性可能在解码步骤中有所不同,例如,开放路线约束在车辆的子路线接近完成时变得更加关键。在每个步骤中对所有约束应用统一注意限制了模型关注最重要约束的能力。
- 多轨迹涉及每个步骤中不同的上下文,为每个上下文重新嵌入节点会造成沉重的计算负担。
- 多任务VRP求解器通常仅使用初始(步骤0)嵌入和当前上下文来精细化步骤 $i$ 的节点表示。这种不对齐的状态可能无法捕获当前解码步骤的状态,从而限制了模型准确表示马尔可夫性质的能力,而这对于连贯的顺序决策至关重要。
贡献
- 从概念上,我们通过学习逐步上下文和节点状态来纠正先前VRP公式中的不对齐,从而实现更准确的状态估计。
- 从方法论上,我们提出了RGCR来将约束要求集成到步骤上下文中,以及TSNR来促进有效精细化并捕获顺序依赖。
- 从实验上,我们的方法在所有已见(分布内)任务和大多数未见(分布外)任务上取得了优越的结果。
方法
省流:改进了多任务的模型框架,主要针对 多任务的不同特征的嵌入 和 解码中上下文中的不同特征的动态信息,相关联。
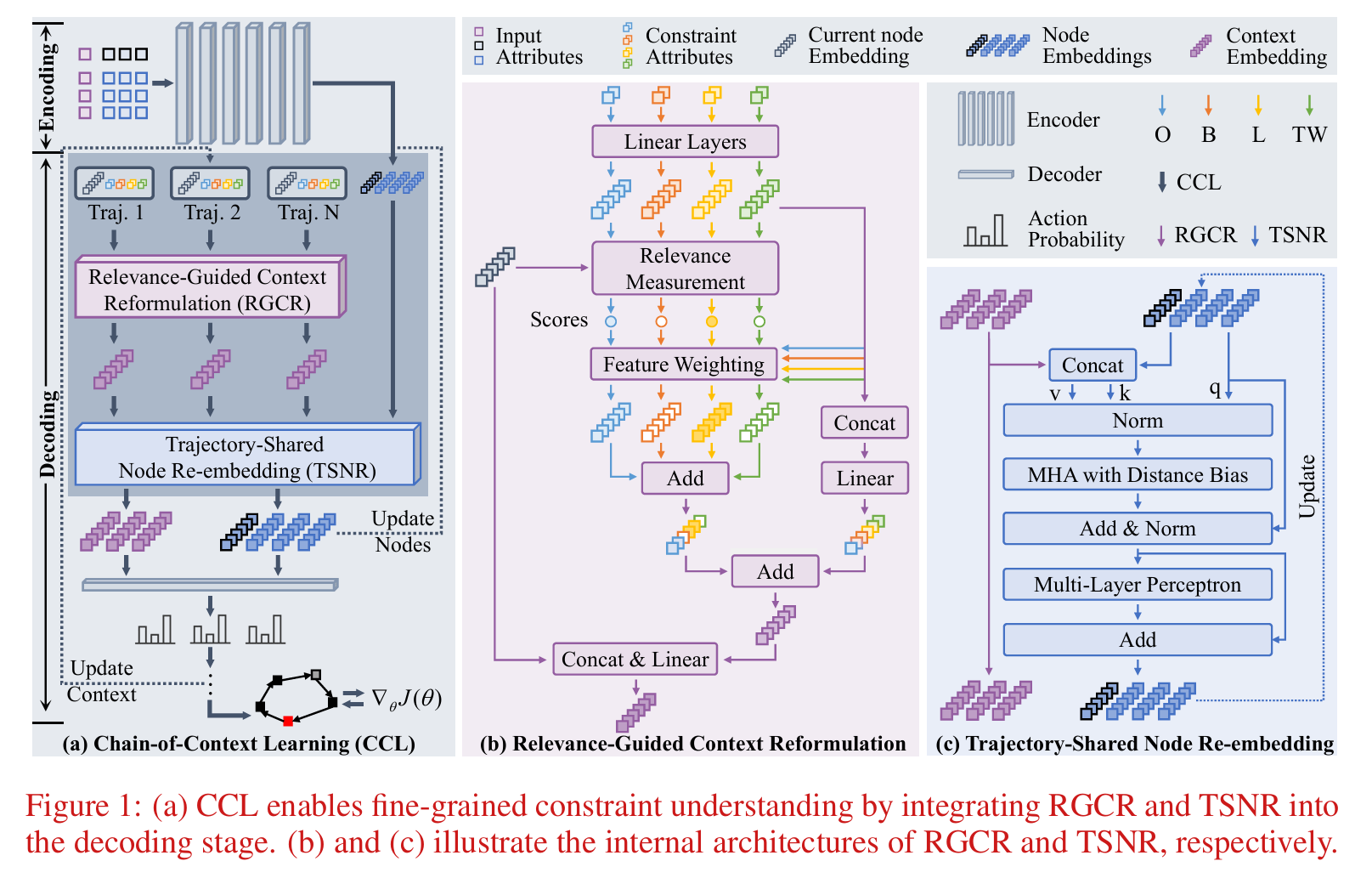
在我们的方法中,我们将上下文和节点状态视为一对,确保两者都反映当前解码步骤的状态。在环境更新期间,我们同时更新两者,以保持上下文和节点信息之间的对齐。
上下文链式学习概述
图1(a)展示了我们提出的上下文链式学习(Chain-of-Context Learning, CCL)的训练工作流程。它采用经典的编码器-解码器范式,在解码阶段集成了相关性引导上下文重构(RGCR)和轨迹共享节点重嵌入(TSNR)。在编码过程中,每个VRP实例(包括约束、车场和节点特征)使用Transformer编码器进行嵌入。来自4种约束(B, L, O, TW)衍生的16个任务的实例被组合成单个批次进行多任务学习。
在基于RL的解码阶段,CCL采用轻量级架构进行决策,从不同的起点并行探索多条轨迹。在每个决策步骤,RGCR聚合约束特定属性和当前节点嵌入以生成上下文嵌入。在收集来自所有轨迹的上下文嵌入后,TSNR通过将它们与多轨迹上下文联合处理来精细化历史节点嵌入。这些精细化的节点嵌入被传递到下一步,逐步影响上下文构建,并在解码步骤中形成上下文链(Chain-of-Context)。构建的上下文和精细化的节点特征一起用于做出决策,所有组件使用RL目标进行联合优化。
推理过程与训练设置类似,只是扩展到评估两种额外约束(即MB和MD)上的泛化能力,这些约束在训练期间被保留用于零样本评估。
编码器
在编码阶段,如图1(a)所示,输入包括约束标签$\tilde{\mathbf{h}}$和节点属性$\mathbf{h} = \lbrace \mathbf{h}_0, \mathbf{h}_1, \ldots, \mathbf{h}_N\rbrace $。这些属性通过基于Transformer的编码器$\mathcal{E}(\cdot)$进行嵌入,产生节点嵌入$\mathbf{H} \in \mathbb{R}^{(N+1) \times D}$:
\[\mathbf{H} = \mathcal{E}(\tilde{\mathbf{h}}, \mathbf{h})\]约束标签$\tilde{\mathbf{h}} \in \mathbb{R}^4$是一个one-hot向量,表示4种约束(即B, O, L, TW)的存在。车场属性$\mathbf{h}_0 = \lbrace c_0^x, c_0^y, o, l\rbrace \in \mathbb{R}^4$包括车场坐标,以及O和L的标签。$\lbrace \mathbf{h}_1, \mathbf{h}_2, \ldots, \mathbf{h}_N\rbrace \in \mathbb{R}^{N \times 7}$是客户特征,每个节点$\mathbf{h}_i = \lbrace [c_i^x, c_i^y], [\delta_i^l, \delta_i^b], [t_i^e, t_i^l, t_i^s]\rbrace $指定坐标、需求和时间窗。
相关性引导上下文重构
在多约束场景中,相关性引导上下文重构(Relevance-Guided Context Reformulation, RGCR)自动学习每个步骤中约束的相对重要性,使模型能够关注最关键的约束。在图1(b)中,RGCR通过三个步骤构建上下文嵌入:
(1)为每个约束生成嵌入,
(2)计算每个约束嵌入与当前节点嵌入之间的相关性,
(3)基于相关性分数自适应地聚合约束嵌入。
在约束嵌入构建中,我们首先提取相应的属性,然后通过单独的线性层进行投影。对于第$i$条轨迹在第$j$个解码步骤,当前节点索引记为$\tau_{i,j}$。每个约束的属性总结如下:
\[\mathbf{c}_{i,j}^B = \lbrace \delta_{\tau_{i,j}}^l, \delta_{\tau_{i,j}}^b, c_{i,j}\rbrace , \quad \mathbf{c}_{i,j}^L = \lbrace c_{\tau_{i,j}}^x, c_{\tau_{i,j}}^y, d_{i,j}\rbrace ,\] \[\mathbf{c}_{i,j}^O = \lbrace c_{\tau_{i,j}}^x, c_{\tau_{i,j}}^y, d_{i,j}'\rbrace , \quad \mathbf{c}_{i,j}^{TW} = \lbrace t_{\tau_{i,j}}^e, t_{\tau_{i,j}}^l, t_{\tau_{i,j}}^s, t_{i,j}\rbrace ,\]其中$\delta^l, \delta^b$表示货运和回程需求,$c_{i,j}$是剩余车辆容量。坐标$c^x, c^y$在二维空间中指定节点位置,$d$是当前子路线的剩余距离,$d’$是总行驶距离。此外,$t^e, t^l, t^s, t$分别表示最早时间、最晚时间、服务时间和当前时间。这些属性分别输入线性层以产生约束嵌入,记为:
\[\mathbf{C}_{i,j}^k = \mathcal{H}(\mathbf{c}_{i,j}^k),\]其中$\mathbf{C}_{i,j}^k \in \mathbb{R}^D$,$k \in \lbrace B, L, O, TW\rbrace $是约束类型,$\mathcal{H}(\cdot)$表示用于投影的线性层。
在相关性计算中,这些约束嵌入与当前节点嵌入交互以产生相关性分数,记为:
\[s_{i,j}^k = \mathbf{H}_{\tau_{i,j}} \cdot \mathbf{C}_{i,j}^k,\]其中$\mathbf{H}_{\tau_{i,j}} \in \mathbb{R}^D$是当前节点嵌入,$\cdot$表示用于计算相关性分数(或相似度)的点积。
在约束聚合中,统一约束嵌入通过将原始和增强的约束嵌入相加获得,记为$\mathbf{S}_{i,j} = \tilde{\mathbf{S}}_{i,j} + \overline{\mathbf{S}}_{i,j}$。原始部分定义为来自公式(5)的四个约束嵌入的拼接:
\[\tilde{\mathbf{S}}_{i,j} = \mathcal{H}(\mathtt{Concat}(\mathbf{C}_{i,j}^B, \mathbf{C}_{i,j}^L, \mathbf{C}_{i,j}^O, \mathbf{C}_{i,j}^{TW})),\]其中$\mathtt{Concat}(\cdot)$表示沿特征维度的拼接,产生大小为$N \times 4D$的拼接嵌入。$\mathcal{H}(\cdot)$是将$4D$输入投影回$D$的线性层,产生$\tilde{\mathbf{S}}_{i,j} \in \mathbb{R}^D$。
对于增强部分,我们对约束嵌入应用加权和:
\[\overline{\mathbf{S}}_{i,j} = s_{i,j}^B \mathbf{C}_{i,j}^B + s_{i,j}^L \mathbf{C}_{i,j}^L + s_{i,j}^O \mathbf{C}_{i,j}^O + s_{i,j}^{TW} \mathbf{C}_{i,j}^{TW}.\]最终上下文嵌入从统一约束和当前节点嵌入中聚合:
\[\tilde{\mathbf{C}}_{i,j} = \mathcal{H}(\mathtt{Concat}(\mathbf{S}_{i,j}, \mathbf{H}_{\tau_{i,j}})).\]轨迹共享节点重嵌入
轨迹共享节点重嵌入(Trajectory-Shared Node Re-embedding, TSNR):为捕获受当前上下文影响的节点特定状态,我们将来自其他节点和多轨迹上下文的上下文语义聚合到节点嵌入中。如图1(c)所示,这通过多头注意机制实现,其中节点嵌入作为查询,统一的节点-上下文信息作为键和值。
形式上,在步骤$j$,我们将$N$条轨迹的上下文嵌入记为:
\[\tilde{\mathbf{C}}_j = \mathtt{Concat}(\tilde{\mathbf{C}}_{1,j}, \tilde{\mathbf{C}}_{2,j}, \ldots, \tilde{\mathbf{C}}_{N,j}),\]其中$\tilde{\mathbf{C}}_j \in \mathbb{R}^{N \times D}$。通过使用上一步的节点$\mathbf{H}_{j-1} \in \mathbb{R}^{(N+1) \times D}$,查询、键和值表示为:
\[\mathbf{q}_j = \mathcal{H}(\mathtt{Norm}(\mathbf{H}_{j-1})), \quad \mathbf{k}_j, \mathbf{v}_j = \mathcal{H}(\mathtt{Norm}(\mathtt{Concat}(\mathbf{H}_{j-1}, \tilde{\mathbf{C}}_j))),\]其中$\mathbf{q}_j \in \mathbb{R}^{N \times D}$,$\mathbf{k}_j, \mathbf{v}_j \in \mathbb{R}^{(N+1) \times D}$。$\mathtt{Norm}(\cdot)$表示均方根归一化层(Root Mean Square, RMS)(Zhang and Sennrich, 2019)。为简洁起见,我们使用相同的符号$\mathcal{H}(\cdot)$表示产生$\mathbf{k}_j$和$\mathbf{v}_j$的模块。
为计算注意力权重,我们进一步加入基于距离的偏置以防止模型对TW过拟合。这个偏置项记为$\mathbf{B}_j = \mathtt{Concat}(\mathbf{d}^{n-n}, \mathbf{d}_j^{c-n})$,由两部分组成:节点-节点和节点-上下文距离:
\[\mathbf{d}^{n-n} = \lbrace d_{m,n} \mid m, n \in \lbrace 0, 1, \ldots, N\rbrace ,\] \[\mathbf{d}_j^{c-n} = \lbrace d_{m,n} \mid m \in \lbrace \tau_{1,j}, \tau_{2,j}, \ldots, \tau_{N,j}\rbrace , n \in \lbrace 0, 1, \ldots, N\rbrace ,\]其中$\mathbf{d}^{n-n} \in \mathbb{R}^{(N+1) \times (N+1)}$,$\mathbf{d}_j^{c-n} \in \mathbb{R}^{N \times (N+1)}$,其每个元素的形式为$d_{m,n} = \mid \mathbf{c}_m - \mathbf{c}_n\mid _2$,其中$\mathbf{c} = \lbrace c^x, c^y\rbrace $表示欧几里得坐标。对于节点-上下文部分,我们提取每条轨迹的当前节点坐标(由$\lbrace \tau_{1,j}, \tau_{2,j}, \ldots, \tau_{N,j}\rbrace $索引)并计算它们到所有候选节点的距离。
注意力权重随后计算为:
\[\mathbf{A}_j = \mathtt{Softmax}(\mathbf{q}_j \mathbf{k}_j^\top / \sqrt{D} + \mathbf{B}_j),\]其中$\mathbf{A}_j, \mathbf{B}_j \in \mathbb{R}^{(N+1) \times (N+1+N)}$,$\mathtt{Softmax}(\cdot)$是softmax操作。
重嵌入的节点表示计算如下:
\[\tilde{\mathbf{H}}_j = \mathbf{q}_j + \mathbf{A}_j \mathbf{v}_j, \quad \mathbf{H}_j = \tilde{\mathbf{H}}_j + \mathtt{MLP}(\mathtt{Norm}(\tilde{\mathbf{H}}_j)).\]我们保留当前步骤的更新节点嵌入$\mathbf{H}_j$,并将其用作下一步的输入查询,更新频率由概率$P_{tr}$(训练)和$P_{ts}$(测试)控制。
逐步决策和训练目标
一旦获得上下文嵌入$\tilde{\mathbf{C}}_j \in \mathbb{R}^{N \times D}$和当前节点嵌入$\mathbf{H}_j \in \mathbb{R}^{(N+1) \times D}$,我们使用它们来预测下一个节点的选择,然后计算RL目标函数以优化模型参数。
在逐步决策阶段,我们采用经典解码器来获取选择下一个节点的概率。该过程表示为:
\[\mathbf{P}_j = \mathcal{D}(\tilde{\mathbf{C}}_j, \mathbf{H}_j, \mathbf{M}_j),\]其中$\mathbf{P}_j \in \mathbb{R}^{N \times (N+1)}$,$\mathcal{D}(\cdot)$表示解码器,而$\mathbf{M}_j$是防止重新访问先前选择节点的掩码。如果满足所有约束,则选择概率最高的节点作为下一个访问节点。否则,选择车场。
在一次交互后,模型生成$N$条解决方案轨迹,每条记为$\tau_i = \lbrace \tau_{i,1}, \tau_{i,2}, \ldots, \tau_{i,N’}\rbrace $,其中$i \in \lbrace 1, 2, \ldots, N\rbrace $,$N’$是总决策步数。然后使用每条轨迹的奖励和所选节点的对数概率计算RL目标,如公式(2)所示。
\[\nabla_\theta J(\theta) = \frac{1}{N} \sum_{i=1}^{N} (R_i - b) \nabla_\theta \log \pi_\theta(a_i \mid s_i),\]其中$i$是轨迹索引,$\pi_\theta(a_i \mid s_i)$表示在给定状态$s_i$下分配给动作$a_i$的概率。$b$是用于减少梯度方差的共享基线,计算为所有轨迹的平均奖励。
实验
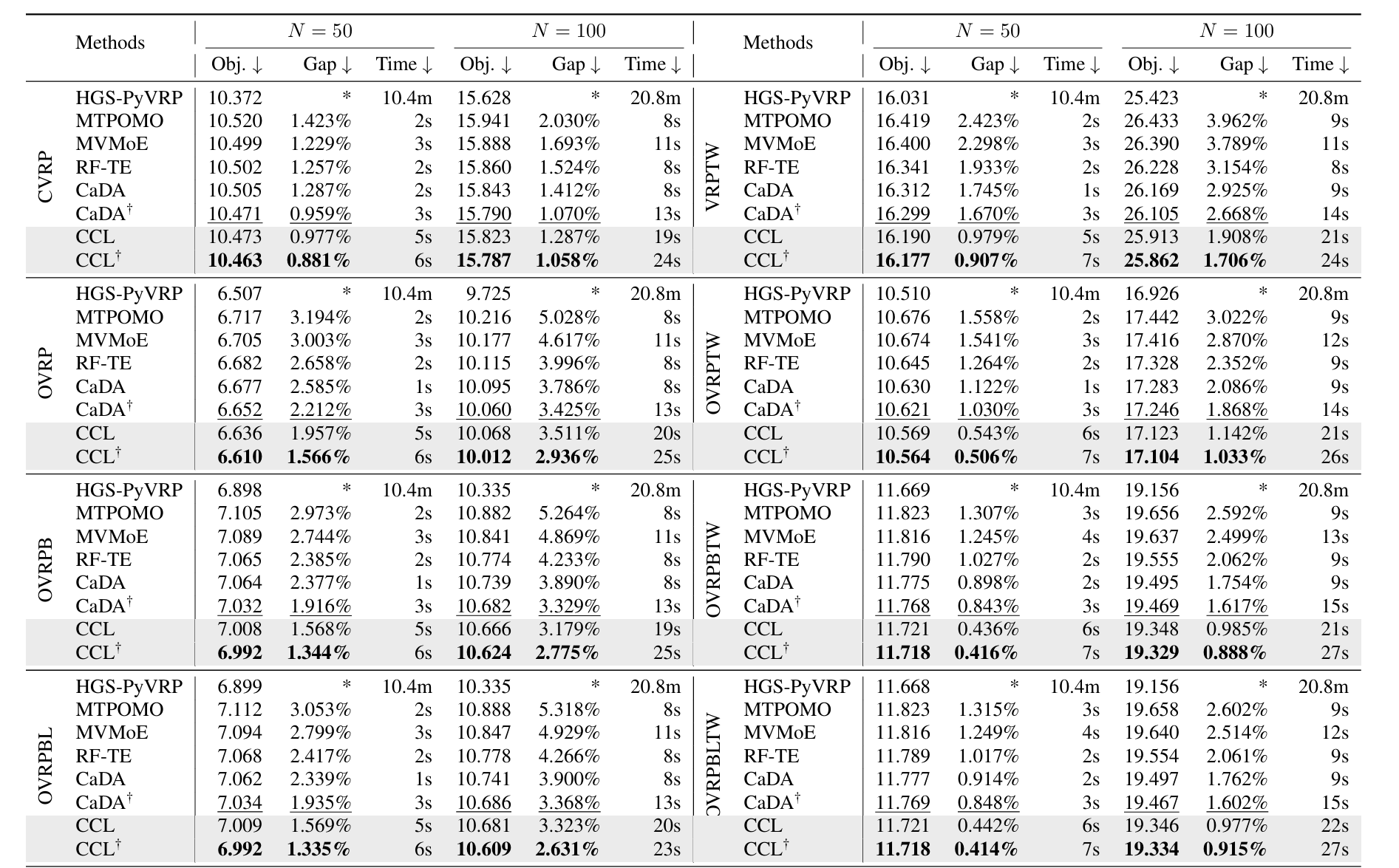
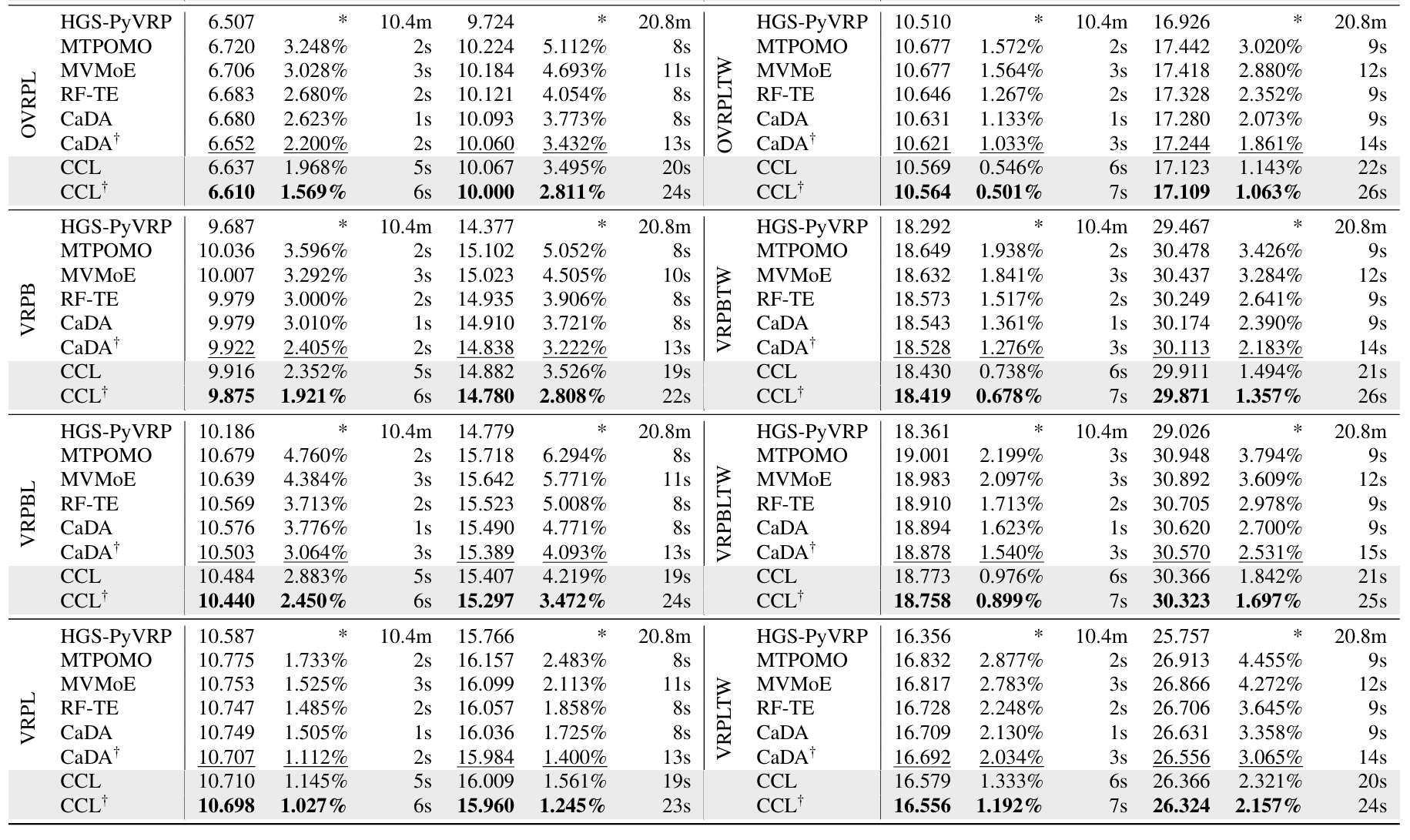
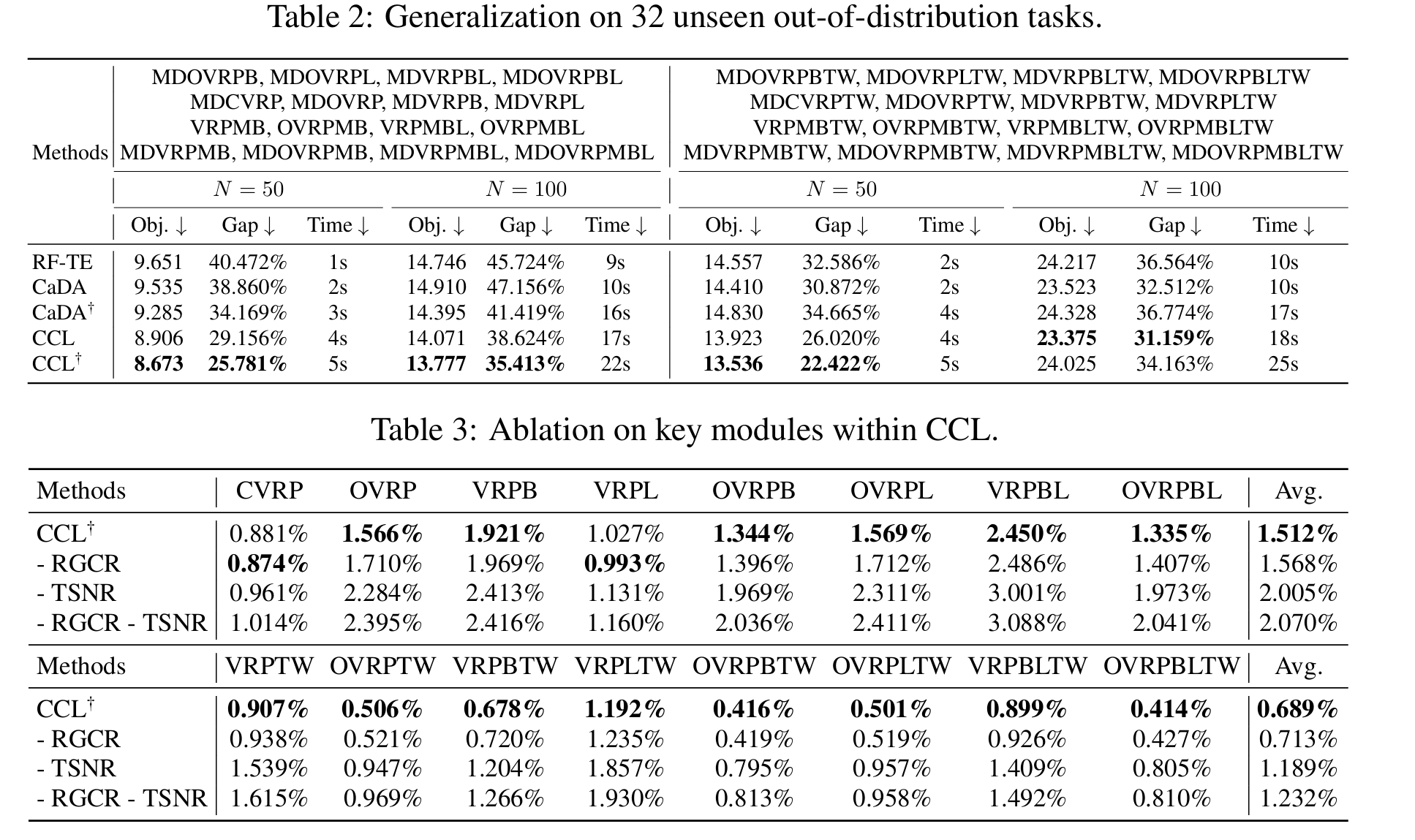
审稿意见
集中在动机不强、创新集中在模型结构的调整而非方法论、提升较小。