RADAR - Learning to Route with Asymmetry-aware Distance Representations

RADAR: Learning to Route with Asymmetry-aware Distance Representations

Hang Yi, Ziwei Huang, Yining Ma, and Zhiguang Cao

ICLR2026，rating：4464

https://openreview.net/forum?id=lWdxX5s9T1

引入

针对非对称问题，现有的方法大多仅针对坐标，难以处理非对称问题。

为解决这一局限性，关键挑战是有效编码不对称距离矩阵的关系结构。在本文中，我们考虑从两个方面对不对称性进行建模：静态不对称性（static asymmetry）和动态不对称性（dynamic asymmetry）。

• 静态不对称性指输入距离矩阵中的方向性差异。
  • 当前的神经求解器主要在两个位置引入静态不对称性：编码器注意力机制和初始化阶段。在注意力机制中，许多方法将点积分数与距离信号拼接以注入静态不对称性信息。
  • 然而，在初始化阶段，编码不对称性本质上是更困难的：不对称成本定义在边级别，而大多数架构在节点级别表示上操作。与欧几里得设置不同，坐标提供了可以完全恢复距离结构的几何支架，不对称矩阵缺乏这种几何结构，使得方向模式更难学习。先前在初始化阶段编码静态不对称性的尝试往往丢失全局结构，因此表现不佳。
• 动态不对称性指在编码器注意力中出现的、依赖于层数的交互差异。
  • 在每一层，$i \rightarrow j$的交互分数与边信号融合后，不必等于$j \rightarrow i$的分数，这些差异随着上下文和深度动态演化。
  • 然而，当前求解器依赖行级softmax注意力，它仅在节点$i$的邻域上积分信息。因此，$A_{i,j}$反映了$i$的局部上下文，但忽略了$j$如何与图的其余部分交互，限制了模型捕获全局距离信息的能力，特别是在不对称设置中。

我们引入RADAR：具有不对称感知距离表示的学习路由。RADAR通过两个关键组件来解决静态和动态不对称性，以学习不对称感知嵌入。

对于静态不对称性，我们提出一种基于成本矩阵奇异值分解（Singular Value Decomposition, SVD）的初始化方案。通过将其分解为左奇异向量和右奇异向量，RADAR学习紧凑的节点嵌入，编码每个节点作为源节点和目标节点的角色，保留全局方向性。

对于动态不对称性，我们将注意力机制中的softmax函数替换为Sinkhorn归一化（Sinkhorn normalization），它对注意力矩阵的行和列进行联合归一化。这强制了平衡的双向流，使注意力分数能够捕获不仅依赖于每个节点自身邻域，还依赖于其对应节点邻域结构的交互。

我们的贡献如下：

1. 我们在现实的不对称距离矩阵下研究神经VRP求解器，推进NCO方法在真实场景中的适用性；
2. 我们引入基于SVD的初始化，从输入距离矩阵捕获全局方向关系，改善跨实例大小的泛化能力。我们还表明Sinkhorn归一化产生显著提升，强调了在注意力期间捕获两个交互节点的完整邻域上下文的重要性；
3. 我们在17个合成和3个真实世界VRP变体上评估RADAR。在所有情况下，RADAR始终优于最先进的基线方法，展现出强劲性能；
4. 我们提供若干深入分析，包括输入的结构特性、坐标在不对称性下的作用，以及不同不对称水平下初始化策略的评估。

方法

省流：

对于静态不对称性，我们提出一种基于成本矩阵奇异值分解（Singular Value Decomposition, SVD）的初始化方案。通过将其分解为左奇异向量和右奇异向量，RADAR学习紧凑的节点嵌入，编码每个节点作为源节点和目标节点的角色，保留全局方向性。

对于动态不对称性，我们将注意力机制中的softmax函数替换为Sinkhorn归一化（Sinkhorn normalization），它对注意力矩阵的行和列进行联合归一化。这强制了平衡的双向流，使注意力分数能够捕获不仅依赖于每个节点自身邻域，还依赖于其对应节点邻域结构的交互。

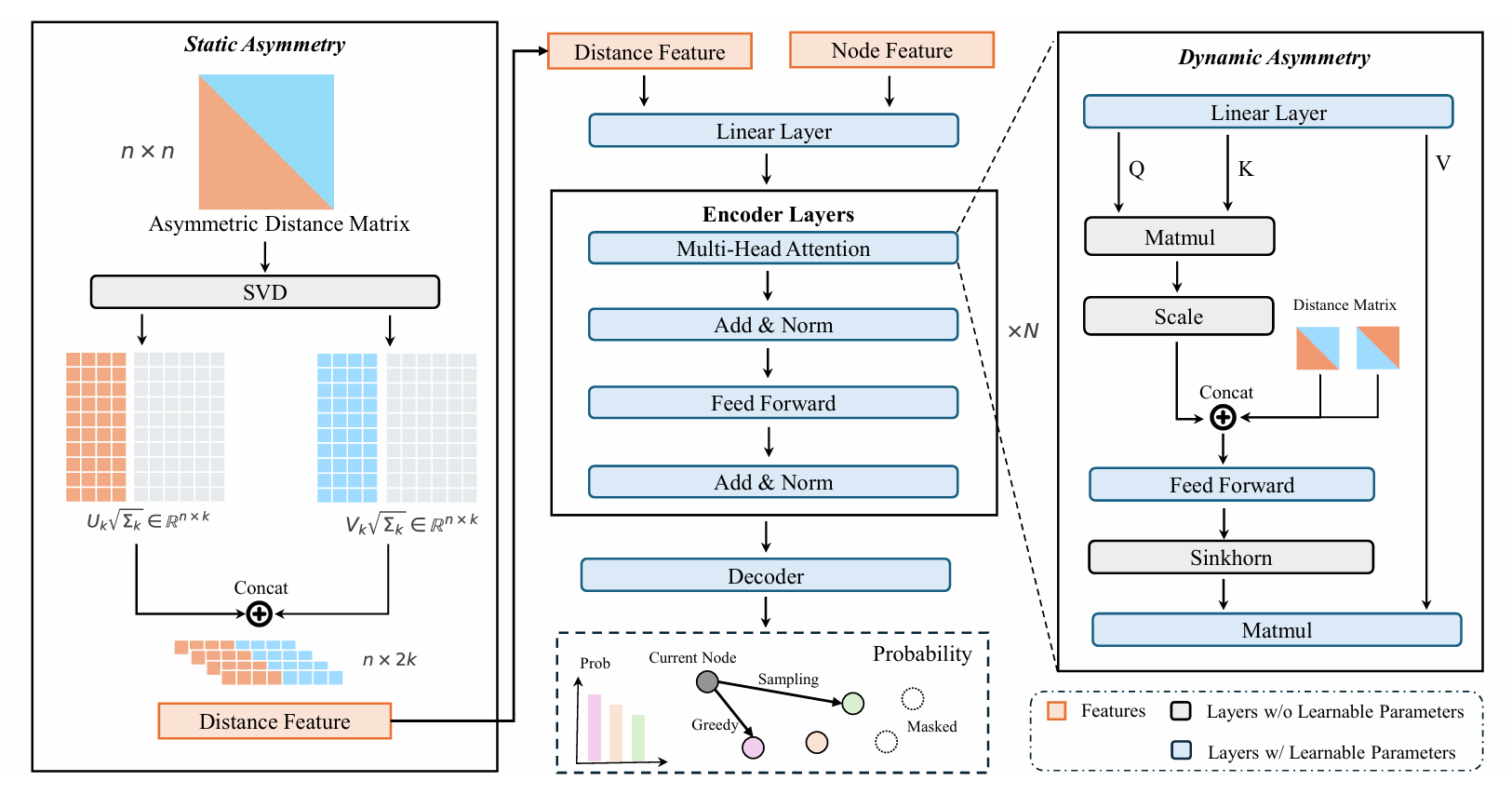
静态不对称性：基于SVD的嵌入

神经VRP架构成功的核心原则是生成既封装节点特定属性（例如需求）又封装图关系特征（例如距离矩阵）的节点嵌入能力。然而，我们强调一个关键点：除非初始节点嵌入是可区分的且捕获方向距离信息，否则大多数此类设计无法有效利用关系结构。当所有节点以相同嵌入开始时，无论注意力权重如何，注意力输出保持相同，因为它们是相同值向量的凸组合。这使得模型无法学习有效的表示。

与欧几里得问题不同，节点的坐标为此类节点嵌入初始化提供了强归纳先验，不对称距离矩阵缺乏这种几何结构，使得生成捕获其固有方向模式的初始节点嵌入变得困难。在没有信息性节点特征的情况下，需要替代初始化策略在关系推理开始之前引入节点特定变化。文献中出现了两种主要方法来解决这一挑战：无信息初始化（uninformed initialization）和有信息初始化（informed initialization）。

无信息初始化在不依赖输入结构的情况下引入节点区分信号。这些方法提供合成可区分的嵌入，例如节点索引、固定位置模式或随机初始化的向量。例如，MatNet用零向量和one-hot向量初始化行和列嵌入。由于每个节点在 $d$ 维空间中需要唯一的one-hot向量，节点数 $n$ 必须不超过 $d$。UNICO引入伪热编码（Pseudo-hot Encoding, POE）以放松大规模问题的维度约束。虽然无信息嵌入可以分配区分性嵌入，但它们引入了缺乏输入语义基础的随机噪声，可能破坏相对于图结构的节点对称性。因此，模型必须学习忽略或覆盖无意义的差异，这可能阻碍学习效率并与任务的结构性归纳偏置不一致。

相比之下，有信息初始化通过利用嵌入在输入边特征中的结构信息（即距离矩阵 $D \in \mathbb{R}^{n \times n}$）来构建节点嵌入。该矩阵编码静态不对称性并捕获实例的整体拓扑。有信息嵌入旨在从这种关系结构直接派生节点表示，而非注入任意信号，允许网络从关系有意义的表示开始。尽管有优势，有信息初始化也提出独特挑战。距离矩阵 $D$ 中的值相互依赖并共同定义实例拓扑。因此，从边空间到节点空间的任何投影可能固有地与节点数 $n$ 纠缠。这种纠缠往往导致特定于大小的嵌入，泛化到与训练时不同大小的问题实例时表现不佳。常见策略是总结每个节点的邻域，例如通过选择其前 $k$ 个最近邻居或基于距离的概率采样邻居，并将获得的局部上下文投影到嵌入空间。然而，这种直接使用原始距离作为节点特征的方法未能捕获图的底层拓扑不对称结构。

为解决现有有信息嵌入的局限性，我们关注嵌入本身及其编码距离矩阵结构信息的能力。距离矩阵的固有不对称性称为静态不对称性。理想情况下，我们希望初始嵌入能够表示静态不对称性。因此，我们引入一个形式化定义来描述嵌入何时可被称为表示静态不对称关系信息。

定义1（不对称感知嵌入）。嵌入矩阵 $X \in \mathbb{R}^{n \times k}$ 被认为相对于特征矩阵 $D \in \mathbb{R}^{n \times n}$ 是不对称感知的，如果存在两个不同的线性变换 $W_1, W_2 \in \mathbb{R}^{k \times k}$ 使得：

该定义形式化了嵌入以与注意力机制兼容的形式表示静态不对称性的能力。注意力计算成对交互为 $QK^\top$。我们采用类似的双线性形式 $X W_1 (X W_2)^\top$，其中 $W_1 \neq W_2$ 以产生反映原始距离矩阵不对称性的非对称交互矩阵。为构建此类嵌入，我们引入截断SVD（Truncated SVD, TSVD）来重建每个节点的相对坐标：

其中 $U_k \in \mathbb{R}^{n \times k}$ 和 $V_k \in \mathbb{R}^{n \times k}$ 分别包含 $D$ 的前 $k$ 个左奇异向量和右奇异向量，$\Sigma_k \in \mathbb{R}^{k \times k}$ 是由前 $k$ 个奇异值组成的对角矩阵。

在成本矩阵中，每个条目 $D_{i,j}$ 表示从节点 $i$（出发）到节点 $j$（到达）的成本。相应地，$D$ 的行对应出发节点，列对应到达节点。基于这种结构，我们可以构建两个中间表示 $X_L$ 和 $X_R$，分别捕获行相关特征和列相关特征。距离特征 $X \in \mathbb{R}^{n \times 2k}$ 定义为 $X_L$ 和 $X_R$ 沿特征维度的拼接：

获得的 $X$ 相对于 $D$ 是不对称感知的，因为存在两个投影矩阵：

使得：

因此，模型理论上通过单个嵌入矩阵捕获静态不对称性。该过程如算法1所示。我们分析了不同截断水平下输入距离矩阵的重建质量。前10个奇异值可捕获约47%的矩阵信息，而30和50个奇异值分别将保留率提高到约76%和89%。我们选择前10个奇异值作为分布内和分布外泛化之间的权衡。

算法1：基于SVD的初始化

输入： 距离矩阵 $D \in \mathbb{R}^{n \times n}$，秩 $k$ 输出： 节点嵌入 $X_{\text{final}}$

1. $\mu \leftarrow \text{Mean}(D)$, $\sigma \leftarrow \text{Std}(D)$
2. $D \leftarrow (D - \mu) / \sigma$
3. $[U, S, V] \leftarrow \text{SVD_lowrank}(D, k)$
4. $Q \leftarrow U \cdot \sqrt{S}$
5. $K \leftarrow V \cdot \sqrt{S}$
6. $X \leftarrow [Q \mid K]$
7. $X_{\text{final}} \leftarrow \text{Linear}(X)$
8. return $X_{\text{final}}$

动态不对称性：Sinkhorn归一化

在不对称VRP中，方向依赖性不仅应在初始化时保留，还应在表示学习期间保留。在基于注意力的编码器中，节点嵌入通过来自其他节点的信息加权聚合逐层动态更新。编码器注意力期间学习的不对称性称为动态不对称性。现有工作通常将距离矩阵直接纳入注意力分数的计算。形式上，从节点 $i$ 到其邻居的注意力由下式给出：

其中 $\text{Sim}(\cdot)$ 表示相似性函数，衡量节点 $i$ 和节点 $j$ 的兼容性，以其嵌入和成对距离为条件。与原始注意力相比，该公式显式将节点到节点的关系信号 $(D_{i,j}, D_{j,i})$ 整合到相似性函数中。随后的行级Softmax在所有 $i$ 的邻居上归一化这些分数，将局部距离信息与邻域中的更广泛关系模式耦合。

然而，这种建模仅使注意力分数 $A_{i,j}$ 感知节点 $i$ 邻域中的距离信息（即 $D_{i,:}$ 和 $D_{:,i}$），而对节点 $j$ 的完整邻域结构（即 $D_{j,:}$ 和 $D_{:,j}$）保持未知。我们假设这一限制削弱了编码器捕获全局方向依赖性的能力，因为 $i$ 和 $j$ 之间的交互在没有考虑 $j$ 自身如何与图其余部分相关的情况下被评估。值得注意的是，这一问题在2D欧几里得设置中不存在，其中整个距离矩阵 $D$ 可从节点坐标重建，因此其信息已嵌入节点表示 $X$ 中。

为解决此问题，我们提出用Sinkhorn归一化（Sinkhorn normalization）替换行级Softmax，它迭代归一化注意力矩阵的行和列，见算法2。这确保每个注意力分数 $A_{i,j}$ 反映对节点 $i$ 和 $j$ 的更完整表征，通过整合直接连接到它们的完整距离关系集。

算法2：Sinkhorn归一化

输入： 分数矩阵 $S \in \mathbb{R}^{n \times n}$，迭代次数 $T$
输出： 归一化矩阵 $P$

1. $P \leftarrow \exp(S)$
2. for $t = 1$ to $T$ do
3. $\quad P \leftarrow P / \sum_{\text{col}}(P)$
4. $\quad P \leftarrow P / \sum_{\text{row}}(P)$
5. end for
6. return $P$

实验

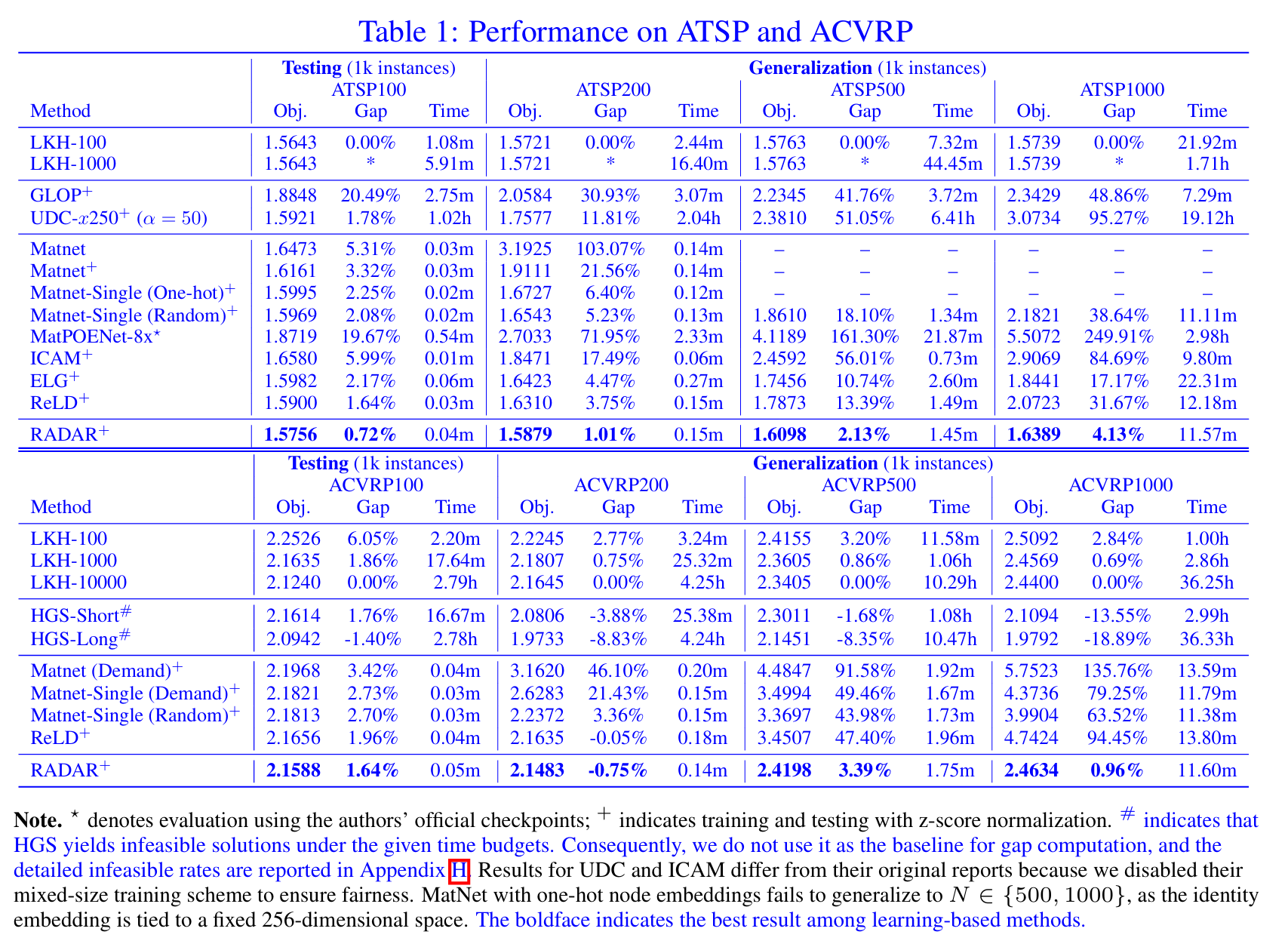
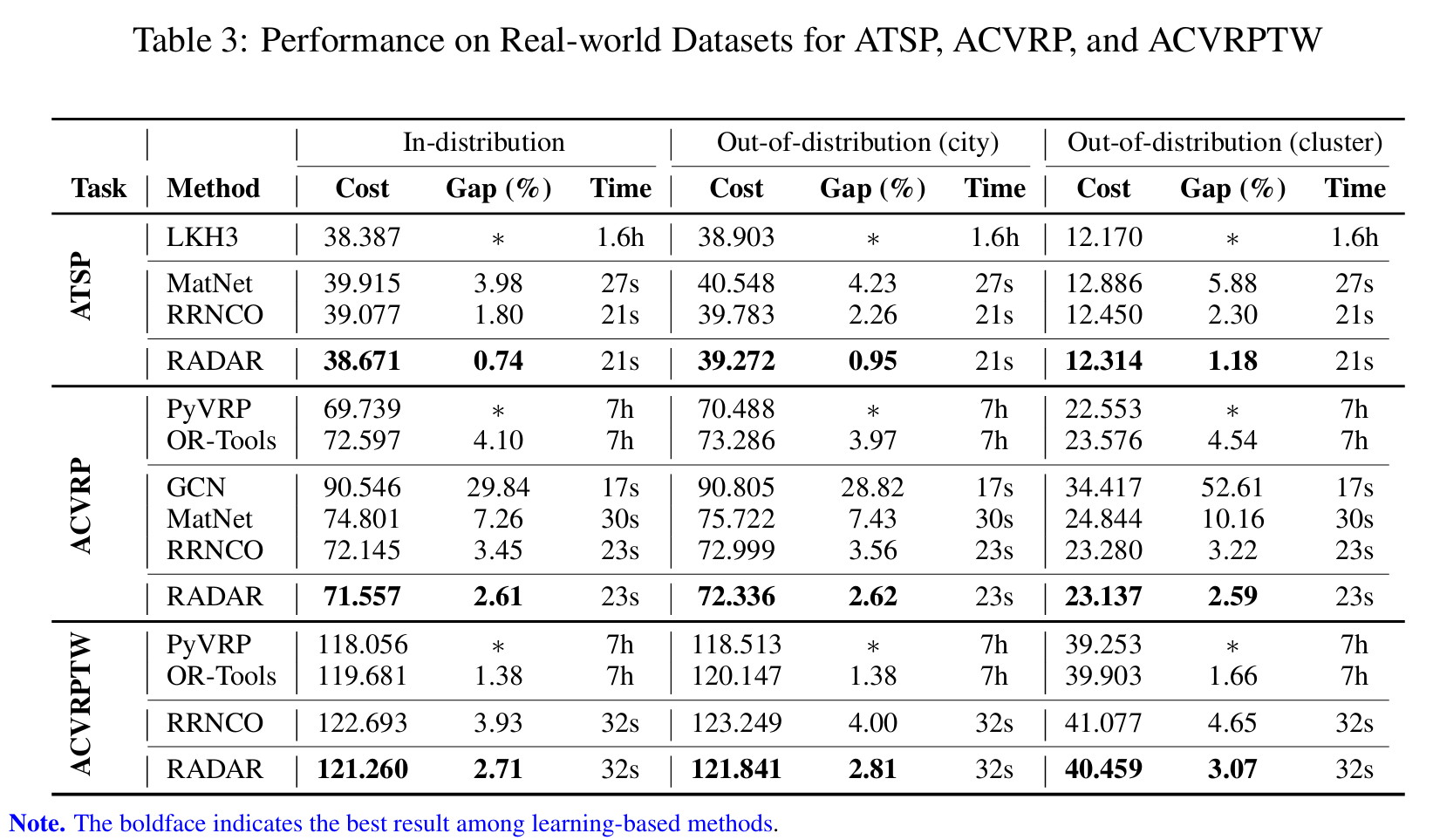
参数分析

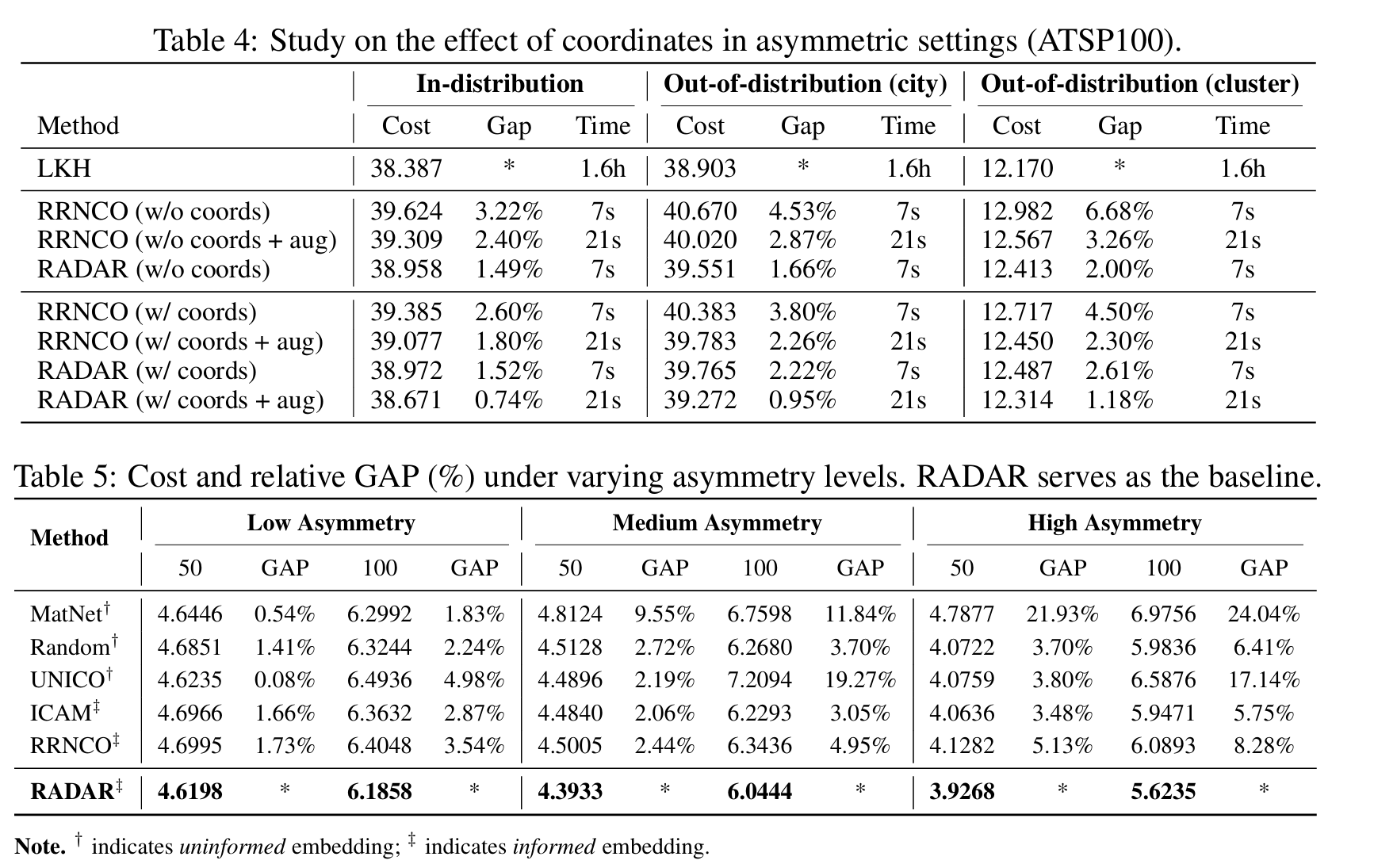
消融实验

审稿意见

创新点是SVD+Sinkhorn的叠加，消融实验不清晰，对比基线的选择和表现有待商榷。

• Previous
  Chain-of-Context Learning - Dynamic Constraint Understanding for Multi-Task VRPs
• Next
  Towards Efficient Constraint Handling in Neural Solvers for Routing Problems