Towards Efficient Constraint Handling in Neural Solvers for Routing Problems
Jieyi Bi, Zhiguang Cao, Jianan Zhou, Wen Song, Yaoxin Wu, Jie Zhang, Yining Ma, and Cathy Wu
ICLR2026,rating:6486
https://openreview.net/forum?id=raDFGuQxvD
目标
复杂约束VPR
挑战
大多数基于RL的NCO求解器通过两种方案处理约束:可行性掩码(feasibility masking)和隐式可行性感知(implicit feasibility awareness)。
-
可行性掩码通过在马尔可夫决策过程(Markov Decision Process, MDP)中排除无效动作来强制执行约束。虽然在简单MDP中有效,但在复杂情况下,计算掩码本身是NP-hard的,例如具有复杂局部搜索算子的神经改进求解器,或具有相互依赖约束的神经构造求解器,如带时间窗的旅行商问题(Traveling Salesman Problem with Time Windows, TSPTW)。此外,即使在可计算的情况下,严格掩码在多约束VRP中的影响往往被忽视。
-
在带有回程、持续时间和时间窗约束的容量限制VRP中强制执行严格掩码会严重阻碍RL收敛到更优策略。近期一系列工作转而探索可行性感知,通过约束相关特征、奖励塑造或近似可学习掩码隐式地通知MDP决策。
思路和贡献
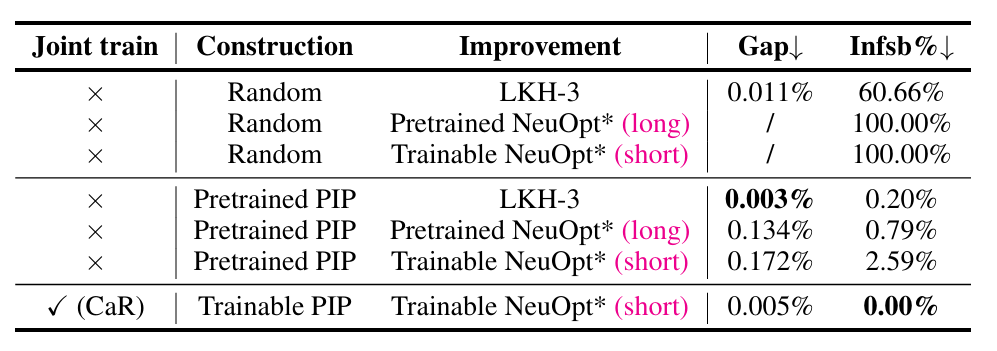
为解决这一问题,我们强调基于学习的可行性细化(learning-based feasibility refinement),这一点在神经求解器中被忽视:与其纯粹专注于通过掩码强制执行可行性或通过特征或奖励隐式学习可行性信号,我们提问RL是否能够在很少的后构造步骤中显式细化不可行解,同时保持最优性。为实现这一点,可以考虑利用现有的搜索技术,如随机重构(Random Reconstruction, RRC)、高效主动搜索(Efficient Active Search, EAS),或混合框架如协作策略(Collaborative Policies, LCP)、RL4CO和NCS。然而,这些方法旨在减少简单VRP上的最优性差距。当应用于硬VRP时,它们可能产生100%的不可行性,或依赖于运行数小时的冗长改进过程,且当在训练或推理期间减少搜索步骤时往往失败。
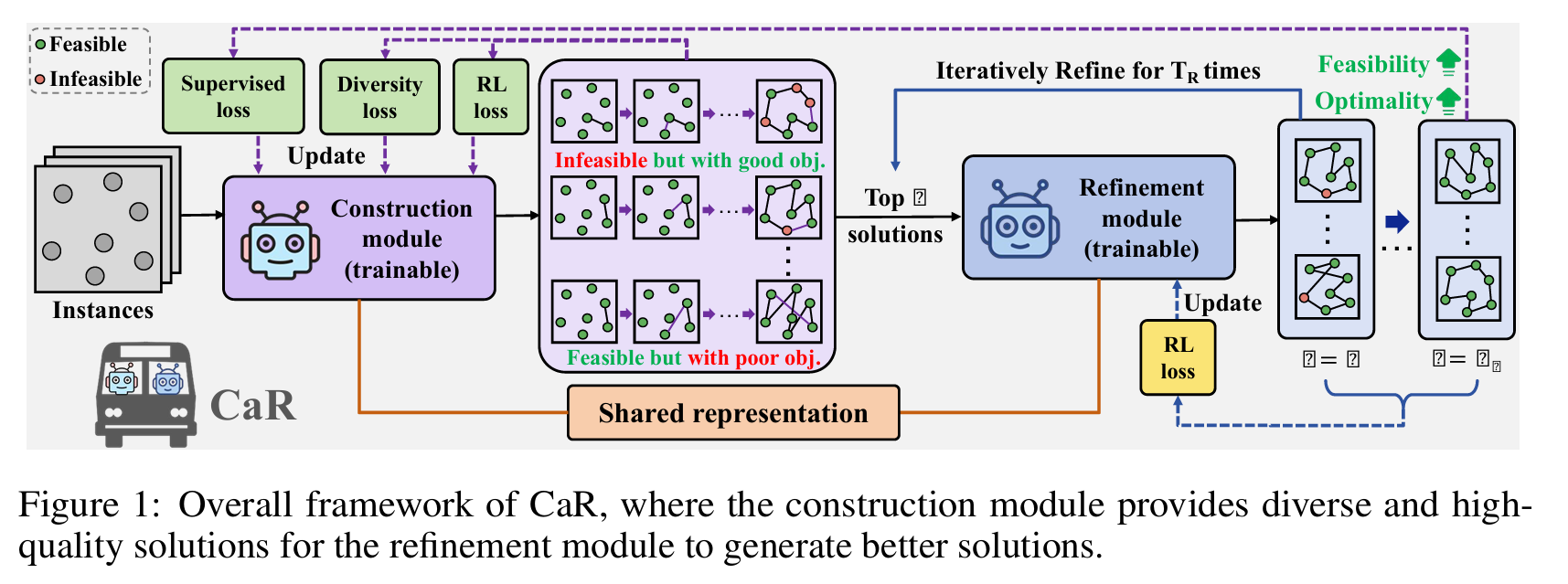
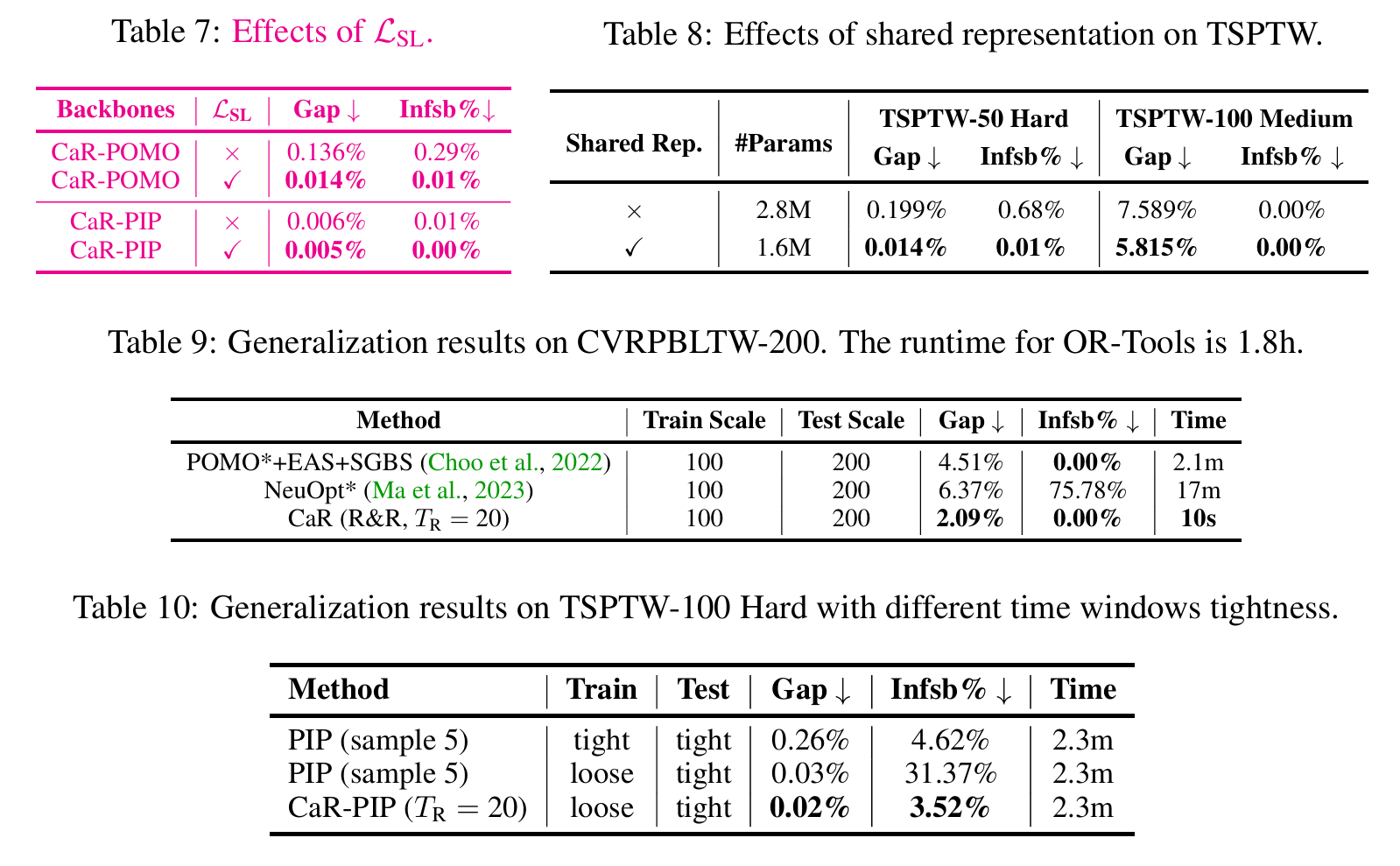
在本文中,我们提出了Construct-and-Refine(CaR),作为一个简单 yet 有效的可行性细化框架,作为迈向通用神经方法进行高效约束处理的第一步。CaR引入了一个端到端的联合训练框架,统一了神经构造模块与神经改进模块。通过设计,它结合了两种范式的互补优势,同时针对效率:构造提供多样且高质量的解,有利于通过我们定制的损失函数引导的快速细化。与依赖繁重改进来减少最优性差距的先验混合方法不同,CaR使用更少的细化步骤,可以将运行时间从小时减少到分钟或秒。此外,提出的可行性细化方案内在地激励了一种新形式的协同可行性感知(synergized feasibility awareness)。CaR因此进一步考虑了一种构造-改进共享表示(construction-improvement-shared representation),用于实现跨范式表示学习,实现潜在的知识共享,从而在更复杂的约束场景中提高性能。
我们的贡献如下:
1) 我们全面分析了现有可行性掩码和隐式可行性感知方案的局限性,并引入了用于高效约束处理的基于学习的可行性细化方案;
2) 我们提出了Construct-and-Refine(CaR),一个简单、通用、保持效率的框架,通过端到端联合训练执行可行性细化,构造适合快速细化的多样且高质量的解,由我们定制的损失函数引导;
3) CaR通过跨范式表示学习实现新颖的协同可行性感知,进一步增强了复杂情况下的约束处理;
4) 实验表明,CaR可能适用于增强大多数基于RL的构造和改进求解器,在解决各种硬约束VRP时,与经典和神经最先进方法相比,提供卓越的可行性、解质量和效率。
方法
现有约束处理方案讨论
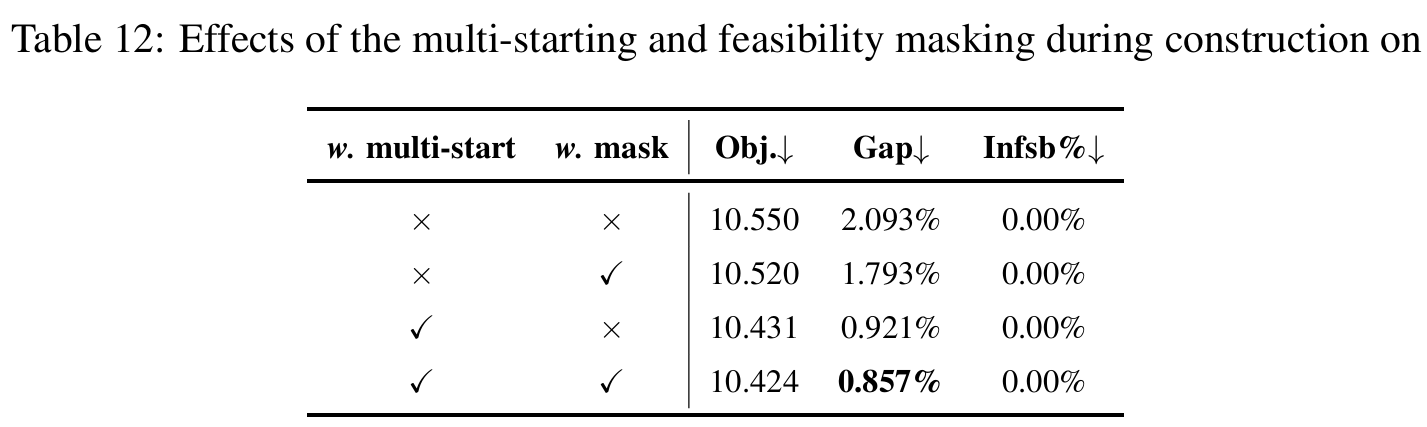
可行性掩码(Feasibility masking)在构造MDP的每个节点选择步骤和改进MDP的每个局部搜索步骤中排除无效动作。它在主流神经求解器中被广泛使用,在VRP约束简单时效果良好。例如,表12显示,在CVRP中移除掩码会将POMO的最优性差距从0.86%增加到0.92%,证实了其有效性。然而,在复杂VRP中,掩码面临两个根本性挑战。
首先,掩码计算本身可能是难处理的。例如,在TSPTW中,在每个构造步骤评估时间相互依赖的可行性需要检查所有未来动作,这是NP-hard的;类似地,在改进求解器中计算局部搜索算子(如k-opt)的可行移动也是难处理的。
其次,即使可处理,掩码在多约束VRP中可能过于严格。例如,在CVRPBLTW中,严格掩码过滤掉超过60%的节点(图6),严重限制搜索空间并阻碍RL收敛到高质量策略(更多讨论见附录E.1)。在这些复杂VRP中,近似掩码或松弛掩码(如表2中POMO*与POMO的比较)提供部分缓解,但无法完全解决这些问题:它们可能仍无法保证可行性、引入计算效率低下或降低解质量。
除了掩码,近期工作转向可行性感知,通过奖励/惩罚或约束相关特征隐式引导MDP决策。然而,前者在Bi等人的研究中被证明在复杂VRP中失去有效性,而后者仅作为策略学习的辅助信号。这激励了通过细化显式处理可行性的替代方案的需求。
与构造模块联合训练可行性细化
为了实现高效的可行性细化,我们利用构造的效率并提出我们的CaR框架。CaR通过联合训练构造和细化,引导构造模块生成适合通过定制损失函数进行快速细化的多样、高质量解。为了有效集成构造和细化,我们设计了一个联合训练框架,在每个梯度步骤中同时优化两个过程,使它们能够共同进化。
如图1所示,对于每批训练实例$\mathcal{G}$,构造模块首先并行生成一小组多样、高质量的初始解。然后这些解在$T_R$步内(即$T_R = 10$对比经典改进方法中的5000步)被轻量级神经改进过程细化,实现对高潜力候选解的快速增强。细化的输出随后监督构造,促进对不可行性和次优性的协同纠正。
构造策略损失(Construction policy loss)。策略$\pi_{\theta}^{\mathrm{C}}$通过REINFORCE训练,损失为:
\[\mathcal{L}_{\mathrm{RL}}^{\mathrm{C}} = \frac{1}{S}\sum_{i=1}^{S}\left[ \left(\mathcal{R}(\tau_i) - \frac{1}{S}\sum_{j=1}^{S}\mathcal{R}(\tau_j)\right) \log \pi_{\theta}^{\mathrm{C}}(\tau_i) \right]\]其中解概率分解为:
\[\pi_{\theta}^{\mathrm{C}}(\tau) = \prod_{t=1}^{\mid \tau\mid } \pi_{\theta}^{\mathrm{C}}(e_t \mid \tau_{<t})\]其中 $\tau_{<t}$ 表示在步骤$t$选择边$e_t$之前的部分解。我们采用带多样展开的组基线来减少方差。对于像CVRP这样的简单变体,$S$个解通过POMO的多启动策略生成,而对于时间约束变体(如TSPTW和CVRPBLTW),我们采样$S$个解以避免不可行性。
构造模块中的定制损失(Tailored losses in construction module)。为了补偿因移除多启动机制而减少的多样性,并增强用于细化的初始构造解的多样性,我们引入辅助的基于熵的多样性损失:
\[\mathcal{L}_{\mathrm{DIV}} = -\sum_{t=1}^{\mid \tau\mid } \pi_{\theta}^{\mathrm{C}}(e_t \mid \tau_{<t}) \log \pi_{\theta}^{\mathrm{C}}(e_t \mid \tau_{<t})\]这在RL训练期间很大程度上鼓励策略探索。为了避免低效,我们使用式(2)中的成本评估候选解,并仅将前$p$个高质量候选解馈送到后续细化。如果细化模块改进了构造解(由$\mathbb{I}=1$指示),则最佳细化解$\tau^\ast$用作伪地面真值来监督$\pi_{\theta}^{\mathrm{C}}$:
\[\mathcal{L}_{\mathrm{SL}} = -\mathbb{I} \cdot \sum_{t=1}^{\mid \tau^\ast\mid } \log \pi_{\theta}^{\mathrm{C}}(e_t^\ast \mid \tau_{<t}^\ast)\]其中$\mathbb{I}$指示此类细化是否导致可行性和目标的改进。最终构造损失整合三个组件:
\[\mathcal{L}(\theta^{\mathrm{C}}) = \mathcal{L}_{\mathrm{RL}}^{\mathrm{C}} + \alpha_1 \mathcal{L}_{\mathrm{DIV}} + \alpha_2 \mathcal{L}_{\mathrm{SL}}\]短视界CMDP的松弛以实现高效细化。基于松弛CMDP表述在构造中的成功,我们将其扩展到细化过程。与先验工作(假设可接受延长运行时间,将改进建模为无限视界MDP)不同,我们采用短视界展开限制$T_R$,平等对待每个步骤,与CaR的高效细化设计一致。
细化策略损失(Refinement policy loss)。 细化策略$\pi_{\theta}^{\mathrm{R}}$在$T_R$步内迭代改进解,步骤$t$处细化解的概率分解为:
\[\pi_{\theta}^{\mathrm{R}}(\tau_t) = \prod_{\kappa=1}^{K} \pi_{\theta}^{\mathrm{R}}(a_{\kappa} \mid a_{<\kappa}, \tau_{t-1})\]其中$K$表示顺序细化移动/动作的总数,更多细节见附录C。步骤$t$的RL损失$\mathcal{L}_{\mathrm{RL}}^{\mathrm{R}}(t)$使用式(3)中的REINFORCE算法计算,其中$S$替换为$p$,因为只有$p$个解被细化。最终细化损失定义为所有$T_R$步骤的平均值:
\[\mathcal{L}(\theta^{\mathrm{R}}) = \frac{1}{T_R}\sum_{t=1}^{T_R} \mathcal{L}_{\mathrm{RL}}^{\mathrm{R}}(t)\]鼓励每个细化步骤都有意义地贡献并提高整体细化效率。
联合训练损失结合上述两个损失:
\[\widetilde{\mathcal{L}}(\theta) = \mathcal{L}(\theta^{\mathrm{C}}) + \omega \mathcal{L}(\theta^{\mathrm{R}})\]其中$\omega$平衡它们的尺度。这种联合损失促进模块之间的信息交换,增强协同处理复杂约束的协同作用。
跨范式表示学习以增强可行性感知
除了通过特征或奖励/惩罚的隐式可行性感知外,我们的可行性细化通过跨范式表示学习自然地增强感知。为了进一步减少开销并促进协同,我们探索构造和细化之间的共享编码器以实现知识转移,特别是在硬约束VRP中。
通过统一编码器的跨范式共享表示。 给定实例批次$\lbrace \mathcal{G}_i\rbrace _{i=1}^{B}$,两种范式都学习通过编码器获得高维节点嵌入$h_i$。对于CVRPBLTW,每个节点$v_i$由其坐标、需求(即送货或取货)、时间窗和持续时间限制表示:
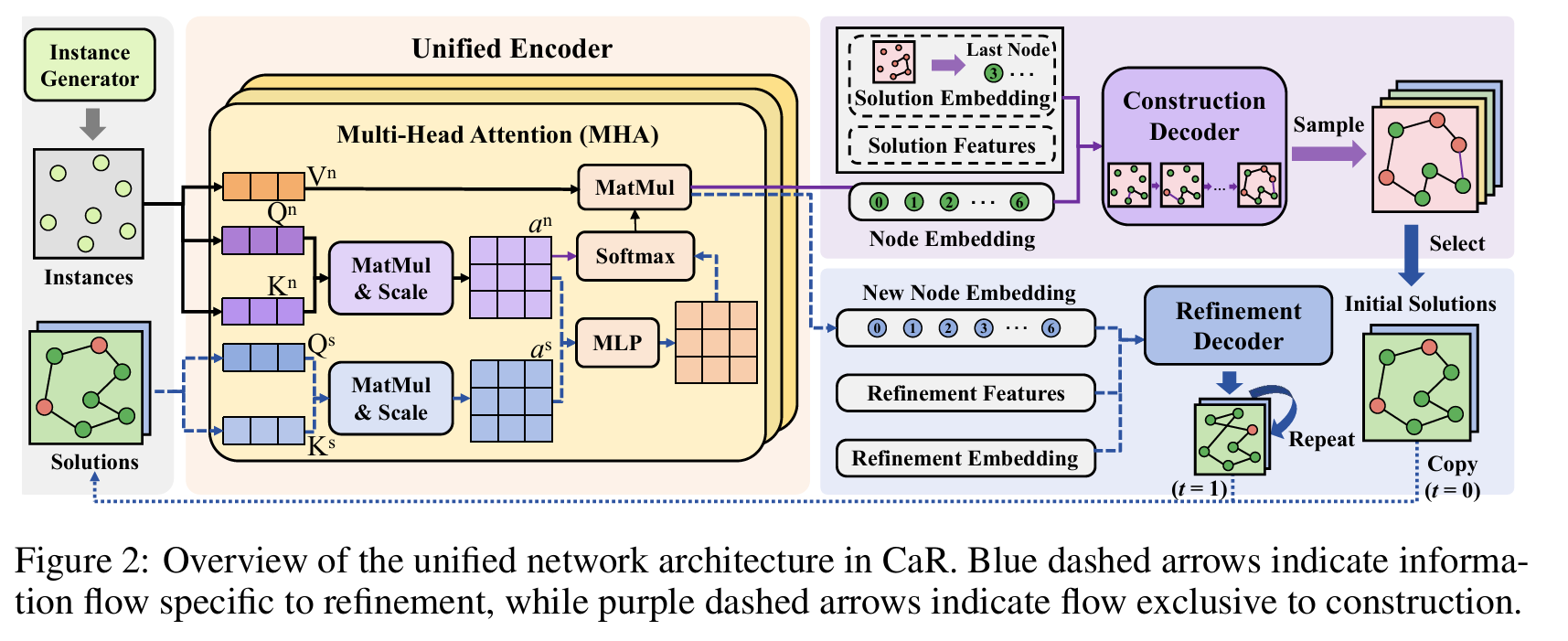
\[f_i^{\mathrm{n}} = \lbrace x_i, y_i, q_i, l_i, u_i, \ell\rbrace\]与构造不同,细化还通过位置信息编码解的顺序结构来整合解特征。为了支持两种范式,我们使用带多头注意力的6层Transformer编码器。仅在细化中需要的位置编码,通过合成注意力机制使用循环位置编码(Cyclic Positional Encoding, CPE)注入。如图2所示,多层感知机(MLP)通过逐元素聚合融合节点级注意力分数$a^{\mathrm{n}}$和来自位置嵌入向量的解级分数$a^{\mathrm{s}}$。
解码器(Decoder)。解码器从节点表示生成动作概率,为构造选择下一个节点或为细化选择修改。在CaR中,我们在一次应用于一个构造和一个改进时保留原始神经求解器设计。为了验证通用性,我们实验了两种构造主干:POMO和PIP,以及两种细化主干:NeuOpt和N2S。
为了将改进求解器适应新变体(如TSPTW、CVRPBLTW),我们遵循其原始设计并引入变体特定特征,如细化历史和节点级可行性信息,以增强约束感知。
实验
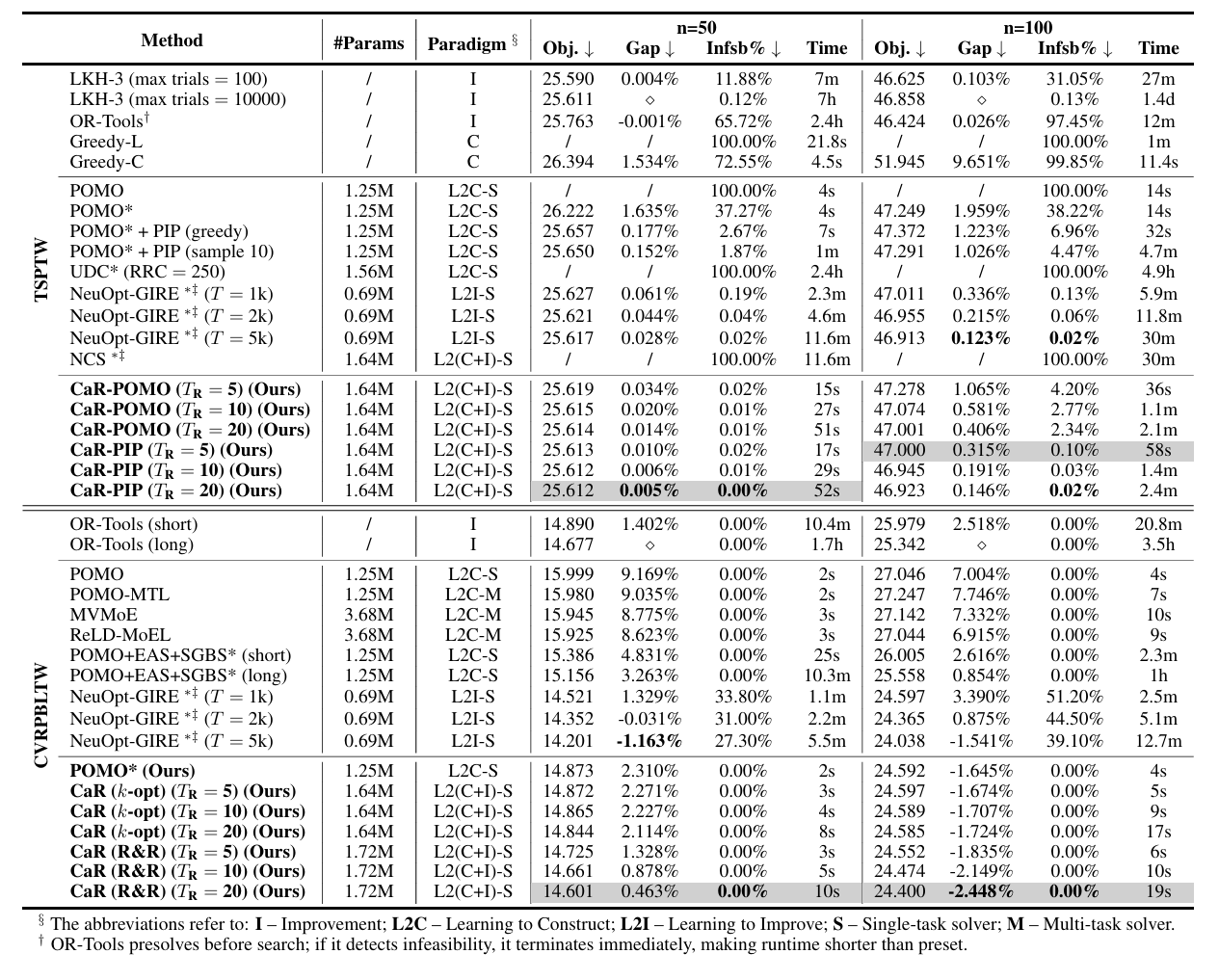
消融实验(两个模型的组件)
审稿意见
主要集中在:构造、精炼、联合微调的概念并不新鲜,贡献有限。