Towards Real-World Routing with Neural Combinatorial Optimization

Jiwoo Son, Zhikai Zhao, Federico Berto, Chuanbo Hua, Zhiguang Cao, Changhyun Kwon, and Jinkyoo Park

ICLR2026，rating：4648

https://openreview.net/forum?id=sKvo9ZZfpe

目标

非对称、真实世界、VRP

省流

提出了一个新的模型，充分利用边和点的信息
设计了一个新的真实世界数据集，并开源了构造方式
代码全部开源

挑战

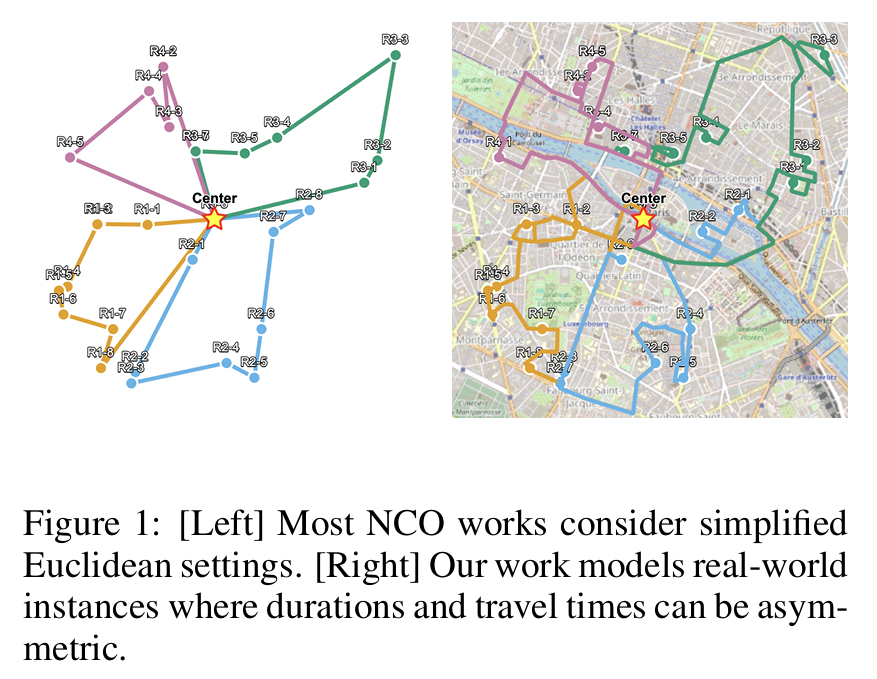
现有的 NCO 方法大多在简化的欧几里得数据集上训练，无法捕捉真实道路网络的非对称性（如单向街、交通拥堵、转弯限制等导致的不对称距离和时间）。
传统 NCO 架构主要基于节点，难以有效处理边特征和相关的非对称成本矩阵。

真实世界VRP的特点：

距离矩阵和持续时间矩阵是非对称的（$d_{ij}\neq d_{ji}$）。
需要同时考虑空间坐标、距离、持续时间、方向角度等多种特征。

方法

关键创新：

自适应节点嵌入（Adaptive Node Embedding, ANE）采用概率加权距离采样——通过学习的上下文门控高效整合空间坐标与非对称距离，避免完整距离矩阵处理同时保留非对称关系；
神经自适应偏置（Neural Adaptive Bias, NAB）——首个在深度路由架构中联合建模非对称距离和持续时间矩阵的可学习机制，用数据驱动的上下文偏置替代自适应注意力自由模块（Adaptation Attention Free Module, AAFM）中的手工启发式规则。该模型使用编码器-解码器架构，其中编码器构建全面的节点表示，解码器顺序生成解决方案，我们的贡献聚焦于增强编码器的真实世界路由能力同时保持效率。

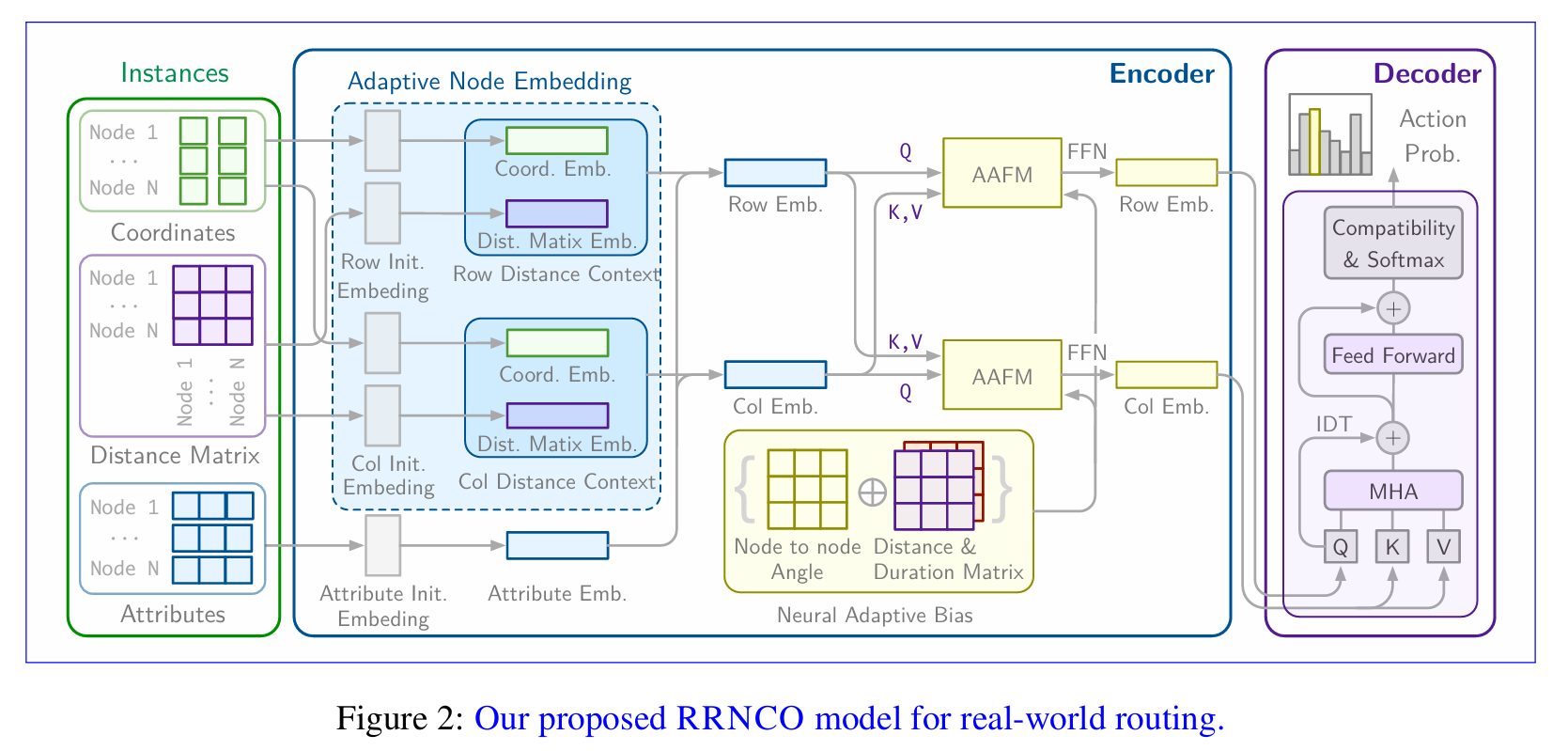
编码器

自适应节点嵌入

自适应节点嵌入模块将距离相关特征与节点特征综合，创建全面的节点表示。我们方法的一个关键方面是有效整合两个互补的空间特征：距离矩阵信息和基于坐标的关系。

对于距离矩阵信息，我们采用选择性采样策略，捕获最相关的节点关系同时保持计算效率。给定距离矩阵 $\mathbf{D} \in \mathbb{R}^{N \times N}$，我们根据与距离成反比的概率为每个节点 $i$ 采样 $k$ 个节点：

\[p_{ij} = \frac{1/d_{ij}}{\sum_{j=1}^{N} 1/d_{ij}}\]

其中 $d_{ij}$ 表示节点 $i$ 和 $j$ 之间的距离。然后，采样的距离通过学习的线性投影转换到嵌入空间：

\[\mathbf{f}_{\text{dist}} = \text{Linear}(\mathbf{d}_{\text{sampled}})\]

坐标信息被单独处理以捕获节点之间的几何关系。对于每个节点，我们首先基于原始坐标计算其空间特征。这些特征然后通过另一个学习的线性变换投影到相同的嵌入空间：

\[\mathbf{f}_{\text{coord}} = \text{Linear}(\mathbf{x}_{\text{coord}})\]

为了有效结合这些互补的空间表示，我们采用上下文门控（Contextual Gating）机制：

\[\mathbf{h} = \mathbf{g} \odot \mathbf{f}_{\text{coord}} + (1-\mathbf{g}) \odot \mathbf{f}_{\text{dist}}\]

其中 $\odot$ 是Hadamard积，$\mathbf{g}$ 表示由多层感知机（MLP）确定的学习门控权重：

\[\mathbf{g} = \sigma(\text{MLP}([\mathbf{f}_{\text{coord}}; \mathbf{f}_{\text{dist}}]))\]

该门控机制允许模型自适应地权衡每个节点基于坐标和基于距离的特征的重要性，实现更细致的空间表示。

为了有效处理非对称路由场景，我们遵循（Kwon et al., 2021）中引入的方法，为每个节点生成双重嵌入：行嵌入 $\mathbf{h}^r$ 和列嵌入 $\mathbf{h}^c$。这些嵌入然后通过学习的线性变换与其他节点特征（如需求或时间窗）结合，产生组合的节点表示：

\[\begin{aligned} \mathbf{h}_{\text{comb}}^r &= \text{MLP}([\mathbf{h}^r; \mathbf{f}_{\text{node}}]) \\ \mathbf{h}_{\text{comb}}^c &= \text{MLP}([\mathbf{h}^c; \mathbf{f}_{\text{node}}]) \end{aligned}\]

其中 $\mathbf{f}_{\text{node}}$ 表示额外的节点特征，如需求或时间窗，这些特征通过额外的线性层进行转换。这种双重嵌入方法使RRNCO模型能够更好地捕获和处理真实世界路由场景中的非对称关系。

用于AAFM的神经自适应偏置

通过我们的自适应嵌入方法建立了全面的节点表示后，RRNCO采用基于Zhou et al.（2024a）的自适应注意力自由模块（Adaptation Attention-Free Module, AAFM）来建模复杂的节点间关系。AAFM在双重表示 $\mathbf{h}_{\text{comb}}^r$ 和 $\mathbf{h}_{\text{comb}}^c$ 上操作，通过我们新颖的神经自适应偏置（Neural Adaptive Bias, NAB）机制捕获非对称路由模式。

AAFM操作定义为：

\[\text{AAFM}(Q, K, V, A) = \sigma(Q) \odot \frac{\exp(A) \cdot (\exp(K) \odot V)}{\exp(A) \cdot \exp(K)}\]

其中：

$Q := \mathbf{W}^Q \mathbf{h}_{\text{comb}}^r$
$K := \mathbf{W}^K \mathbf{h}_{\text{comb}}^c$
$V := \mathbf{W}^V \mathbf{h}_{\text{comb}}^c$

具有可学习的权重矩阵 $\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V$。

虽然自适应偏置 $A$ 启发式地定义为 $-\alpha \cdot \log(N) \cdot d_{ij}$（具有可学习的 $\alpha$、节点数 $N$ 和距离 $d_{ij}$），但我们引入了神经自适应偏置（NAB），直接从数据中学习非对称关系。

NAB处理距离矩阵 $\mathbf{D}$、角度矩阵 $\boldsymbol{\Phi}$（其元素 $\phi_{ij} = \arctan2(y_j - y_i, x_j - x_i)$），以及可选的持续时间矩阵 $\mathbf{T}$，实现对真实世界路由中固有的空间-时间非对称性的联合建模。

设 $\mathbf{W}_D, \mathbf{W}_\Phi, \mathbf{W}_T \in \mathbb{R}^{E \times E’}$ 且 $\mathbf{W}_D’, \mathbf{W}_\Phi’, \mathbf{W}_T’ \in \mathbb{R}^{E’ \times E}$ 为可学习的投影矩阵：

\[\begin{aligned} \mathbf{D}_{\text{emb}} &= \text{ReLU}(\mathbf{D}\mathbf{W}_D)\mathbf{W}_D' \\ \boldsymbol{\Phi}_{\text{emb}} &= \text{ReLU}(\boldsymbol{\Phi}\mathbf{W}_\Phi)\mathbf{W}_\Phi' \\ \mathbf{T}_{\text{emb}} &= \text{ReLU}(\mathbf{T}\mathbf{W}_T)\mathbf{W}_T' \end{aligned}\]

然后，我们应用上下文门控来融合这些异构信息源。当持续时间信息可用时，我们采用具有softmax归一化的多通道门控机制：

\[\mathbf{G} = \text{softmax}\left(\frac{[\mathbf{D}_{\text{emb}}; \boldsymbol{\Phi}_{\text{emb}}; \mathbf{T}_{\text{emb}}]\mathbf{W}_G}{\exp(\tau)}\right)\]

其中 $[\mathbf{D}_{\text{emb}}; \boldsymbol{\Phi}_{\text{emb}}; \mathbf{T}_{\text{emb}}] \in \mathbb{R}^{B \times N \times N \times 3E}$ 是所有嵌入的拼接，$\mathbf{W}_G \in \mathbb{R}^{3E \times 3}$ 是可学习的权重矩阵，$\tau$ 是可学习的温度参数。

融合表示计算为：

\[\mathbf{H} = \mathbf{G}_1 \odot \mathbf{D}_{\text{emb}} + \mathbf{G}_2 \odot \boldsymbol{\Phi}_{\text{emb}} + \mathbf{G}_3 \odot \mathbf{T}_{\text{emb}}\]

最后，通过将融合嵌入 $\mathbf{H}$ 投影到标量值获得自适应偏置矩阵 $\mathbf{A}$：

\[\mathbf{A} = \mathbf{H}\mathbf{w}_{\text{out}} \in \mathbb{R}^{B \times N \times N}\]

其中 $\mathbf{w}_{\text{out}} \in \mathbb{R}^E$ 是可学习的权重向量。得到的 $\mathbf{A}$ 矩阵作为学习的归纳偏置，捕获距离、方向角度和旅行持续时间相互作用产生的复杂非对称关系。

神经自适应偏置（NAB）然后通过自适应注意力自由模块（AAFM）整合。具体地，我们通过用NAB生成的自适应矩阵替换通用矩阵 $\mathbf{A}$ 来采用式（10）中定义的操作。

经过 $l$ 次通过AAFM后，NAB产生最终的节点表示 $\mathbf{h}_F^r$ 和 $\mathbf{h}_F^c$。这些表示是RRNCO编码过程的结果，利用距离、角度和持续时间的联合建模来捕获真实世界路由网络中的复杂非对称模式。

解码器

解码器架构整合了来自ReLD和MatNet的关键元素，使用编码器产生的密集节点嵌入来自回归地构建解决方案。在每个解码步骤 $t$，它将行和列节点嵌入与封装当前部分解决方案状态的上下文向量一起作为输入，例如最后访问的节点和动态属性如剩余容量。

该上下文作为多头注意力机制中的查询，以从嵌入中聚合信息，随后是残差连接和多层感知机来细化查询向量。得到的查询然后用于兼容性层中计算可行节点的选择概率，整合负对数距离启发式以优先选择附近选项并增强探索效率。

该设计使我们的模型能够动态地将静态嵌入适应到不断演变的上下文，在各种车辆路径问题上产生强大的性能。

真实世界数据集

我们开发了一个全面的数据生成流程，利用OpenStreetMap路由引擎（OSRM）为全球100个多样化城市创建详细的拓扑地图。每个地图包括位置坐标以及相应的非对称距离和持续时间矩阵。此外，我们设计了一种高效的在线子采样方法，用于生成无限数量的VRP实例以训练我们的强化学习智能体。这种方法确保我们的模型在忠实代表真实世界路由挑战的数据上进行训练。

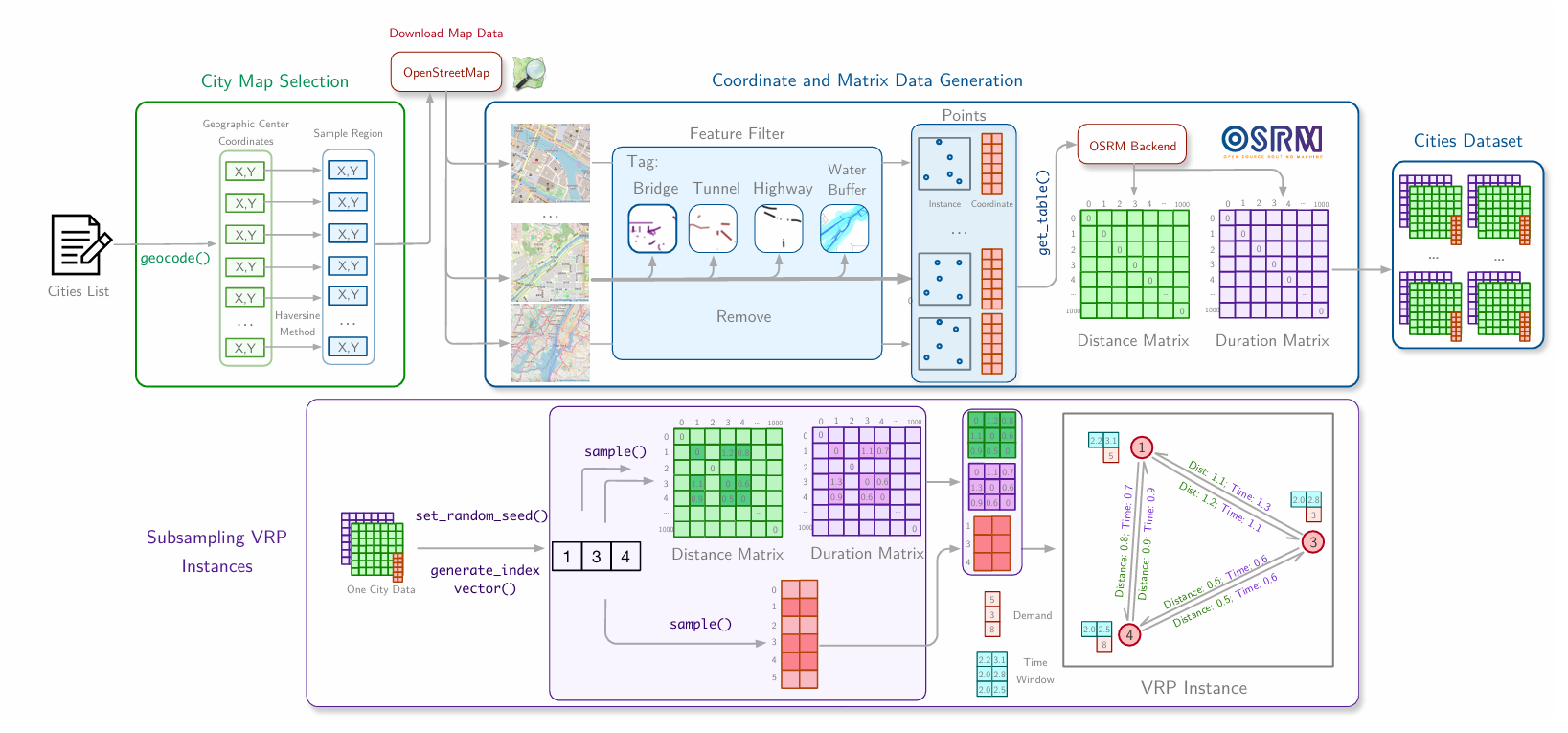
我们设计了一个三步流程来创建多样且现实的车辆路径数据集，旨在训练和测试NCO模型：

城市选择：基于多维城市描述符（形态、交通流模式、土地利用混合）选择全球城市。
拓扑数据生成：使用开源路由机（Open Source Routing Machine, OSRM）创建具有拓扑数据的城市地图，生成精确的位置坐标以及它们之间的对应距离和持续时间矩阵。
VRP实例子采样：高效地子采样这些拓扑以生成多样化的VRP实例，通过添加需求和时间窗等路由特定特征，从而在保留固有空间关系的同时，能够快速生成具有不同运营约束的实例。

阶段一：城市选择

我们选择了分布在六大洲的100个城市列表：

亚洲：25个
欧洲：21个
北美洲：15个
南美洲：15个
非洲：14个
大洋洲：10个

选择通过多个维度强调城市多样性，包括：

人口规模：50个大城市（>100万居民）、30个中等城市（10万-100万）、20个小城市（<10万）
基础设施发展阶段
城市规划方法

城市具有各种布局，从曼哈顿的网格系统到巴黎的放射状模式和菲斯的有机发展，代表从沿海到山区位置的不同地理和气候背景。我们在优先考虑数据可靠性的可用性的同时，在全球公认的都市区和不太知名的城市中心之间取得平衡，为在多样化真实世界条件下评估车辆路径算法提供全面的基础。

此外，通过包括发展中国家的城市，我们旨在推进可能使欠发达地区受益并促进其社会经济发展的交通优化研究。

阶段二：拓扑数据生成框架

在第二阶段，我们生成捕获真实城市复杂性的基础地图。该拓扑数据生成本身由三个关键组件组成：地理边界信息、道路网络中的点采样和旅行信息计算。

地理边界信息

我们为每个目标城市建立标准化的9平方公里区域（3×3公里），以市政坐标为中心，确保不同城市环境之间的相同空间覆盖。

鉴于由于地球的球面几何，相同的物理距离在不同纬度对应不同的经度跨度，我们需要精确的距离计算方法：因此，空间边界使用Haversine球面距离公式计算：

\[d = 2R \cdot \arcsin\left(\sqrt{\sin^2\left(\frac{\Delta\phi}{2}\right) + \cos(\phi_1)\cos(\phi_2)\sin^2\left(\frac{\Delta\lambda}{2}\right)}\right)\]

其中：

$d$ 是沿大圆的两点之间的距离
$R$ 是地球半径（约6371公里）
$\phi_1$ 和 $\phi_2$ 是点1和点2的纬度（弧度）
$\Delta\phi = \phi_2 - \phi_1$ 表示纬度差
$\Delta\lambda = \lambda_2 - \lambda_1$ 表示经度差

这使得能够进行精确的空间边界计算和标准化的跨城市比较，同时在不同地理位置保持一致的分析区域。

阶段三：VRP实例子采样

从大规模城市基础地图中，我们通过子采样一组位置及其相应的距离和持续时间矩阵来生成多样化的VRP实例，使我们能够在保留底层结构的同时有效生成无限数量的实例。

子采样过程遵循另一个三步程序：

1. 索引选择

给定包含 $N_{\text{tot}}$ 个位置的城市数据集，我们定义子集大小 $N_{\text{sub}}$ 表示要为VRP实例采样的位置数量。我们生成索引向量：

\[\mathbf{s} = (s_1, s_2, \ldots, s_{N_{\text{sub}}})\]

其中每个 $s_i$ 从 ${1, \ldots, N_{\text{tot}}}$ 中抽取，确保唯一选择。

2. 矩阵子采样

使用 $\mathbf{s}$，我们从预计算的距离矩阵 $\mathbf{D} \in \mathbb{R}^{N_{\text{tot}} \times N_{\text{tot}}}$ 和持续时间矩阵 $\mathbf{T} \in \mathbb{R}^{N_{\text{tot}} \times N_{\text{tot}}}$ 中提取子矩阵，形成实例特定的矩阵：

\[\begin{aligned} \mathbf{D}_{\text{sub}} &= \mathbf{D}[\mathbf{s}, \mathbf{s}] \in \mathbb{R}^{N_{\text{sub}} \times N_{\text{sub}}} \\ \mathbf{T}_{\text{sub}} &= \mathbf{T}[\mathbf{s}, \mathbf{s}] \in \mathbb{R}^{N_{\text{sub}} \times N_{\text{sub}}} \end{aligned}\]

保留所选位置之间的空间关系。

3. 特征生成

每个VRP可以有不同的特征。例如，在非对称容量约束VRP（ACVRP）中，我们可以生成需求向量 $\mathbf{d} \in \mathbb{R}^{N_{\text{sub}} \times 1}$，使得：

\[\mathbf{d} = (d_1, d_2, \ldots, d_{N_{\text{sub}}})^\top\]

其中每个 $d_i$ 表示位置 $s_i$ 的需求。

类似地，我们可以扩展到ACVRPTW（带时间窗），表示为 $\mathbf{W} \in \mathbb{R}^{N_{\text{sub}} \times 2}$，其中：

\[\mathbf{W} = \{(w_1^{\text{start}}, w_1^{\text{end}}), \ldots, (w_{N_{\text{sub}}}^{\text{start}}, w_{N_{\text{sub}}}^{\text{end}})\}\]

定义每个节点的有效服务间隔。

与以前离线生成静态数据集的方法不同，我们的RRNCO生成框架在几毫秒内动态生成实例，减少磁盘内存消耗同时保持高多样性。

我们的方法使我们能够从总计约1.5GB的相对小的基础拓扑地图集中生成（任意）大量问题实例，相比之下，以前的工作需要数百GB的数据才能产生仅几千个实例。

额外数据信息

我们提出了一个全面的城市出行数据集，涵盖全球不同地理区域的100个城市。对于每个城市，我们在整个相同大小的城市区域收集了1000个采样点。数据集包括每个采样点的精确地理坐标（纬度和经度）。

此外，我们计算并存储了每个城市内所有点对之间的完整距离和旅行时间矩阵，导致每个城市有1000×1000矩阵。

我们数据集中的城市在其特征方面表现出显著的多样性，包括：

人口规模（从小到大）
城市布局模式（如网格、有机、混合和历史布局）
独特的地理特征（沿海、山区、河流、山谷等）

该数据集涵盖多个区域，包括亚洲、大洋洲、美洲、欧洲和非洲。这种城市环境的多样性使得能够对不同城市背景和地理环境下的出行模式进行全面分析。

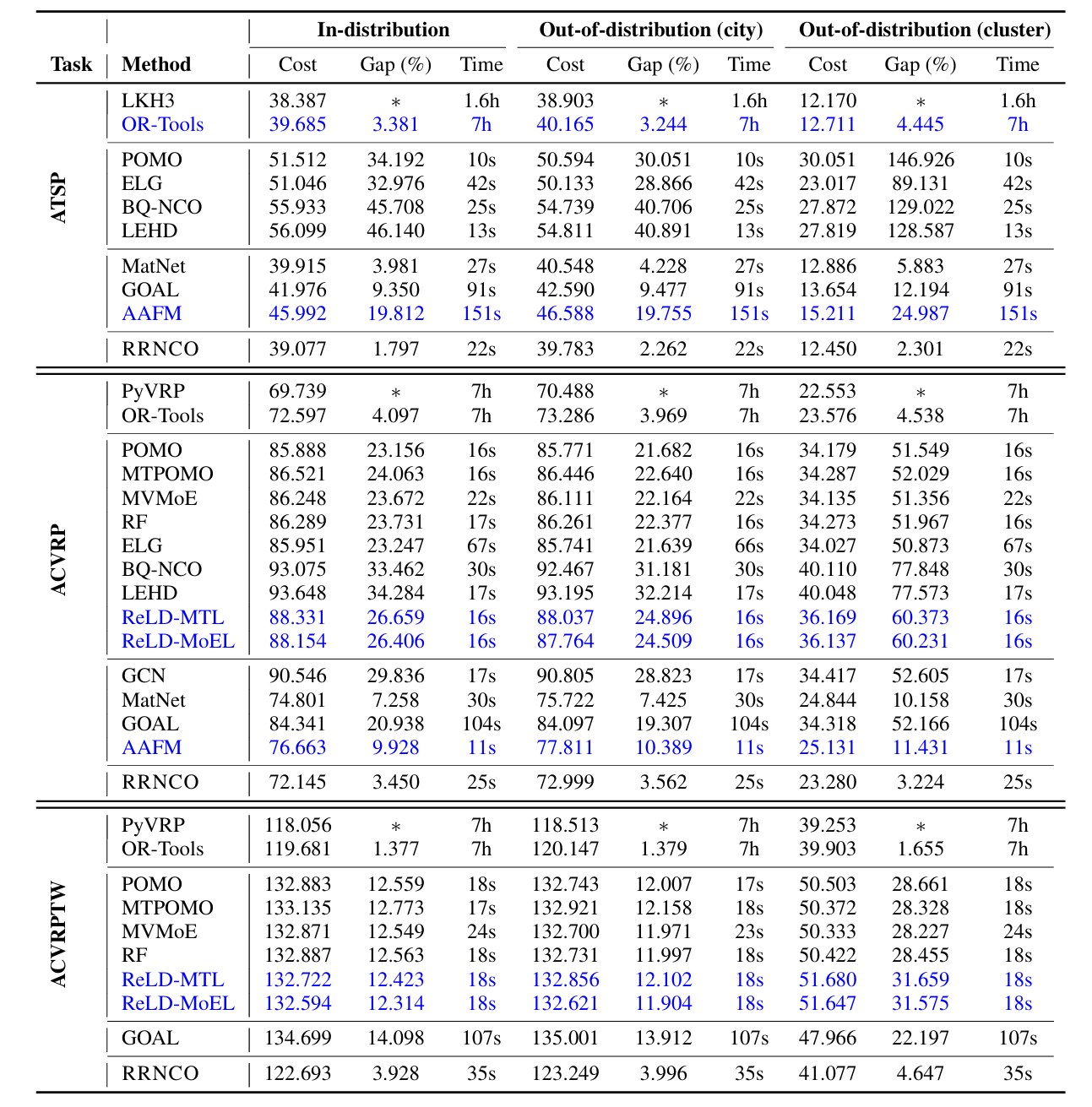
实验

经典baseline：

LKH3：一种在（A）TSP问题上具有强大性能的启发式算法
PyVRP：一种具有全面约束处理能力的VRP专用求解器
Google OR-Tools：一种用于CO的多功能优化库

基于学习的方法：

纯节点编码学习方法：
- POMO：一种基于注意力机制的端到端多轨迹强化学习方法
- MTPOMO：POMO的多任务变体
- MVMoE：MTPOMO的专家混合变体
- RF：一种用于VRPs的基于强化学习的基础模型
- ELG：一种路由问题的局部和全局策略混合方法
- BQ-NCO：一种使用监督学习训练的仅解码器Transformer
- LEHD：一种基于监督学习的重解码器模型
- AAFM：在ICAM框架中引入的注意力自由替代方案，实现实例条件自适应
节点和边编码学习方法：
- GCN：一种用于路由的具有边信息编码的图卷积网络
- MatNet：一种通过矩阵编码边特征的基于强化学习的求解器
- ReLD-MTL 和 ReLD-MoEL：通过恒等映射和前馈解码器细化显著改进跨尺寸和跨问题泛化
- GOAL：一种通过监督学习为包括路由在内的多个CO问题训练的通用智能体

训练配置 我们为了公平比较，在我们的模型、用于ATSP和ACVRP的MatNet以及用于ACVRP的GCN上执行相同设置的训练运行。纯节点模型不需要重新训练，因为我们的数据集已经在 [0,1]x[0,1]坐标范围内标准化（位置均匀采样），我们不重新训练基于监督学习的模型，因为它们需要标记数据。

该模型在4× NVIDIA A100 40GB GPU上训练约24小时。

测试协议 测试数据包括：

In-dist：来自训练期间见过的80个城市生成的新实例的分布内评估
OOD (city)：新城市地图上的分布外泛化
OOD (cluster)：跨地图新位置分布的分布外泛化

测试批量大小为32，数据增强因子为8应用于所有模型，除了基于监督学习的模型（即LEHD、BQ-NCO和GOAL）。所有评估在配备Intel(R) Xeon(R) CPU @ 2.20GHz的NVIDIA A6000 GPU上进行。